Способы выражения составов многокомпонентных систем смесей

Способы выражения составов многокомпонентных смесей

Состав многокомпонентной смеси — раствора, смеси газов или паров, многокомпонентного твёрдого вещества — и, в частности, содержание в ней какого-либо компонента, может выражаться разными способами: как с помощью безразмерных единиц — долей или процентов, так и через размерные величины — концентрации.

В теории массообмена наиболее употребительны следующие величины, выражающие содержание компонента в системе:

1. Объёмная доля — безразмерное отношение объёма компонента «А» ко всему объёму системы.

Обозначение объёмной доли компонента — «j».

Формально доля — безразмерное отношение, но фактически единицей измерения объёмной доли является: [(м 3 А)/(м 3 смеси)].

2. Молярная доля — безразмерное отношение количества вещества компонента «А» к количеству вещества системы.

Обозначения: молярная доля компонента в жидкой фазе — «х», в газовой (паровой) фазе — «у».

В строгой записи у символа доли «х» или «у» (впрочем, как и у символа объёмной доли «j»), должен фигурировать нижний индекс «А».

Фактическая единица измерения молярной доли: [(моль А)/(моль смеси)].

3. Массовая доля — безразмерное отношение массы компонента «А» ко всей массе системы.

Обозначения: массоваядоля компонента в жидкой фазе — « 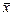», в газовой (паровой) фазе — « ».

Заметим, что в теории массообмена используются специфические обозначения массовой доли: не «w», как это принято в химии, а « 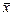» или « ». Это обусловлено тем, что обычно требуется обозначить не только способ выражения состава (здесь — массовая доля), но и указать, в какой именно фазе содержится компонент, а в дополнение к этому — в каком именно месте аппарата (на входе, на выходе, в другом определённом месте аппарата) таково содержание компонента. Применение буквы «w» потребовало бы обилия соответствующих индексов.

Фактическая единица измерения массовой доли: [(кг А)/(кг смеси)].

4. Молярная концентрация — величина, равная отношению количества вещества компонента «А» ко всему объёму системы.

Используемый в химии термин «молярность» – синоним термина «молярная концентрация», – в теории массообмена не применяется.

Обозначения: молярная концентрация компонента в жидкой фазе — «с_х», в газовой (паровой) фазе — «с_у».

Единица измерения молярной концентрации: [(моль А)/м 3 ].

5. Массовая концентрация — величина, равная отношению массы компонента «А» ко всему объёму системы.

Обозначения: массовая концентрация компонента в жидкой фазе — « », в газовой (паровой) фазе — « ».

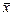
Как видим, в теории массообмена для обозначения массовой концентрации принят символ « » (вероятно, по аналогии с символами массовой доли — « » или « »), а не «r_А» — символ, используемый в химии.

Единица измерения массовой концентрации: [(кг А)/м 3 ].

6. Молярное отношение — безразмерное отношение количества вещества компонента «А» к количеству других веществ системы.

Обозначения: молярное отношение компонента в жидкой фазе — «Х», в газовой (паровой) фазе — «Y».

Фактическая единица измерения: [(моль А)/(моль В)], где символом «В» обозначены все вещества смеси за исключением «А».

7. Массовое отношение — безразмерное отношение массы компонента «А» к массе остальных компонентов системы.

Обозначения: массовое отношениекомпонента в жидкой фазе — « 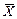», в газовой (паровой) фазе — « ».

Фактическая единица измерения: [(кг А)/(кг В)].

Разнообразие в способах выражения составов фаз продиктовано тем, что, в силу специфики того или иного массообменного процесса, его расчёт удобнее выполнять с использованием определённого выражения содержания компонента. В то же время, исходная информация может быть представлена в иных единицах измерения концентрации.

Так, например, содержание компонента в газовой фазе часто указывается в объёмных долях потому, что именно в объёмных долях отградуированы шкалы многих приборов – газоанализаторов.

Соотношения между различными способами выражения составов многокомпонентных смесей

Установить соотношения между различными способами выражения содержания компонента в системе несложно.

Если содержание компонента «А» в газовой фазе задано как объёмная доля, то в 1 м 3 газовой смеси содержится j_А [м 3 компонента «А»] и (1 – j_А) [м 3 компонента «В»]. В этом случае объёмное отношение компонента «А»:

. (2.1)

Следовательно, массовое отношение компонента «А» в смеси:

. (2.2)

Поскольку для определения плотности газа при рабочих условиях почти всегда используются справочные данные о плотности при нормальных физических условиях (r 0 ) и уравнение Клапейрона – Менделеева, то

. (2.3)

Тогда молярное отношение компонента «А» в газовой смеси:

, (2.4)

где М_А и М_В – молярные массы компонентов «А» и «В», соответственно.

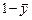
Если же рассматривается 1 кг смеси, в котором массовая доля компонента «А» составляет [(кг А)/(кг см.)], то массовая доля компонента «В» в смеси равна ( ) [кг В/кг см.]. Очевидно

. (2.5)

Отсюда следует, что

. (2.6)

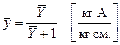
Подставляя сюда выражение для из (2.3), получаем

. (2.7)

Проводя аналогичные рассуждения для 1 моль газовой смеси, в которой молярная доля компонента «А» равна у [(моль А)/(моль смеси)], а доля компонента «В» — (1 – у) [(моль В)/(моль смеси)], имеем:

, (2.8)

. (2.9)

Подставляя сюда выражение для Y из (2.4), получаем

. (2.10)

Фигурирующее в формулах (2.4) и (2.10) отношение 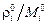представляет собой величину, обратную молярному объёму [при нормальных физических условиях]:

. (2.11)

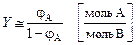
Если считать, что молярный объём любого газа при физически нормальных условиях примерно одинаков ( м 3 /моль), то в таком случае из формулы (2.4) получаем

, (2.12)

а из формулы (2.10) —

, (2.13)

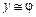
то есть, в отдельных случаях допустимо считать, что молярная доля компонента в газовой фазе приблизительно равна его объёмной доле.

Если для отдельных компонентов и для газовой смеси в целом применимо уравнение Клапейрона – Менделеева, то можно записать:

(2.14)

, (2.15)

где n_A – количество вещества компонента «А»;

п – количество вещества смеси;

R = 8314,41 Дж/(кмоль∙К) – универсальная газовая постоянная;

р – общее давление в системе;

p_A – парциальное давление компонента «А» газовой смеси.

Разделив уравнение (2.14) на (2.15) и сократив равные величины, получаем:

. (2.16)

Отношение представляет собой молярную долю компонента в смеси; следовательно

. (2.17)

В то же время в формуле (2.14) отношение есть не что иное, как молярная концентрация компонента «А» газовой смеси.

В результате имеем соотношение:

. (2.18)

Формулы (2.1), (2.5), (2.6), (2.8), (2.9) могут применяться не только к газовым, но и к жидким смесям, только, разумеется, с заменой в этих формулах букв «игрек» на буквы «икс».

Отношения как способ выражения состава смеси

Итак, содержание компонента в смеси может быть выражено по-разному — и через концентрации, и через доли (объёмные, массовые, молярные).

Может возникнуть вопрос: «Зачем вводить ещё какие-то “отношения”, когда и так существует немало различных способов выражения состава?»

Ответ был дан выше. Здесь повторим: в некоторых случаях в силу специфики массообменного процесса его анализ или расчёт удобнее всего выполнять, применяя именно отношения.

Вот простой пример.

Пусть имеются газовая фаза, состоящая из азота и аммиака, и жидкая фаза, состоящая из воды и аммиака.

Как известно, аммиак в воде растворяется очень хорошо. (Впрочем, также хорошо аммиак улетучивается из водного раствора. Каждому химику, и не только химику, знаком запах нашатырного спирта.) Азот в воде растворим чрезвычайно мало; в дальнейшем считаем, что азот совсем не растворяется в воде. Также полагаем, что молекулы Н₂О не испаряются и не попадают в газовую фазу.

Представим себе некоторый вертикальный аппарат (рис.1), в котором созданы такие условия, что может происходить поглощение аммиака жидкой фазой из газовой фазы, то есть происходить очистка азота от аммиака. (Как отмечено выше, при определённых условиях аммиак может и десорбироваться, то есть выделяться из жидкой фазы в газовую; но здесь и сейчас речь пойдёт только о предназначении одного из способов выражения содержания компонента в смеси).

В аппарат сверху непрерывно подаётся жидкий поглотитель — вода с небольшим содержанием растворённого в ней аммиака, то есть слабый (неконцентрированный) раствор. Так же непрерывно жидкая фаза отводится из аппарата снизу в виде обогащённого [аммиаком] поглотителя.

Пусть в тот же аппарат снизу непрерывно подаётся газовая смесь азота и аммиака. Пройдя через аппарат, газовая фаза отводится из аппарата сверху.

Очевидно, при условиях проведения процесса содержание NH₃ в жидкой фазе увеличивается от верхнего сечения аппарата до нижнего; увеличивается и расход жидкой фазы в целом (как массовый расход, так и расход количества вещества). Содержание NH₃ в газовой фазе от нижнего до верхнего сечения аппарата уменьшается; уменьшается и расход газовой фазы.

В реальных аппаратах фазы каким-то образом распределены друг в друге. Например, газовая фаза распределена в виде пузырей в жидкой фазе. Фазы отделены друг от друга (потому они и называются «фазами») хаотично изменяющейся поверхностью раздела.

Теперь представим тот же аппарат в виде условного объекта, в котором имеется фиксированная поверхность раздела фаз А‑А (рисунок 2), так что по одну сторону от неё (слева на рисунке) движется сплошная жидкая фаза, а по другую (справа на рисунке) — сплошная газовая фаза

— NH₃

— N₂

Рисунок 3

— H₂O

На рис. 2 ширина окрашенной фигуры в том или ином горизонтальном сечении пропорциональна расходу. На том же рисунке интенсивность окраски фигуры соответствует содержанию аммиака в фазе.

Как видно из этого рисунка, в нижнем сечении аппарата расходы обеих фаз максимальны, а в верхнем сечении — минимальны.

Далее представим, что в каждом сечении мы отсортировали молекулы NH₃ от молекул Н₂О в жидкой фазе, и молекулы NH₃ от молекул N₂ в газовой фазе (рисунок 3).

На этом рисунке молекулы NH₃ имеют условную красную окраску, молекулы H₂O — синюю, а молекулы N₂ — жёлтую.

Из рисунка 3 видно, что как количество молекул Н₂О, так и их масса в каждом сечении одинаковы, поскольку принято, что молекулы Н₂О не испаряются и не попадают в газовую фазу.

Количество и масса молекул N₂ так же неизменны в каждом сечении аппарата, так как принято, что азот совсем не растворяется в воде.

По этой причине в расчётах удобнее всего оперировать постоянными расходами так называемых инертных [к массообмену] носителей (в данном примере — расходами именно Н₂О в жидкой фазе и N₂ в газовой фазе). Очевидно, в расчётных уравнениях будут фигурировать только два параметра — два постоянных расхода носителей, вместо четырёх параметров: расходов жидкой фазы на входе в аппарат и на выходе из него и расходов газовой фазы на входе и на выходе из аппарата.

Содержание распределяемого компонента (NH₃) в фазах при этом следует выражать в отношениях.

В данном примере массовые отношения аммиака в фазах [(кг NH₃)/(кг Н₂О)] и [(кг NH₃)/(кг N₂)], а молярные отношения этого компонента — Х [(моль NH₃)/(моль Н₂О)] и Y [(моль NH₃)/(моль N₂)].

[1] Закон открыт нем. учёным А. Фиком (A. Fick, 1855).

Источник