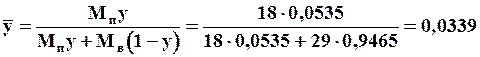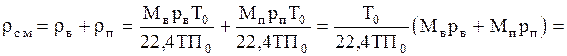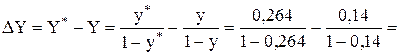Способы выражения состава фаз двухкомпонентных систем жидкость газ приведите соответствующие формулы

Основные зависимости и расчетные формулы

МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА

РОССИЙСКОЙ ФЕДЕРАЦИИ

ИЖЕВСКАЯ ГОСУДАРСТВЕННАЯ СЕЛЬСКОХОЗЯЙСТВЕННАЯ АКАДЕМИЯ

КАФЕДРА “ПРОЦЕССЫ И АППАРАТЫ”

Проректор по учебной работе

доцент __________ А. И. Любимов

“_____”_____________ 1998 г.

Основы массопередачи. Абсорбция. Ректификация

Методическое руководство к решению примеров и задач по курсу “Процессы и аппараты”

Ижевск -1998 г.

Иванов В. И. — к. т. н., заведующий кафедрой “Процессы и аппараты.” ИжГСХА.

Касаткин В. В. — Заведующий кафедрой “Механизация переработки сельскохозяйственной прдукции.”

Ответственный за выпуск — заведующий кафедрой “Процессы и аппараты” к. т. н., доцент Иванов В. И.

Одобрено и рекомендовано к изданию методической комиссией факультета механизации сельского хозяйства ИжГСХА.

Зак. Тир. п. л. ИжГСХА 199__г.

СОДЕРЖАНИЕ

Глава 1. Основы массопередачи. Абсорбция.

Основные зависимости и расчетные формулы 2

Примеры 21

Глава 2. Перегонка и ректификация.

Основные зависимости и расчетные формулы 50

Примеры 59

Основы массопередачи. Абсорбция

Основные зависимости и расчетные формулы

1. Способы выражения состава фаз двухкомпонентных систем жидкость-газ (пар) представлены в табл. 1.1.

Формулы для пересчета концентраций (в жидкой фазе) даны в табл.1.2. Для газовой (паровой) фазы справедливы те же соотношения, но с заменой обозначений x на y, X на Y, С_X на С_y

2. Концентрация компонента в газовой фазе может быть выражена так же через его парциальное давление. На основании уравнений Клайперона и Дальтона мольная (объемная) доля у любого компонента смеси идеальных газов равняется:

где р-парциальное давление компонента газовой смеси; П=р_А+р_В+р_С+. -общее давление смеси газов или паров, равное сумме парциальных давлений всех компонентов.

3.Законы межфазного равновесия для идеальных растворов.

где р*-парциальное давление компонента в газовой фазе; над равновесной с газом жидкостью; x-мольная доля компонента в жидкости; Е-коэффициент Генри, зависящий от температуры и от природы газа и жидкости.

Значения Е для водных растворов некоторых газов даны в табл.XLI.

Подставляя в уравнение (1.2) значение р*=y*П по уравнению (1.1), получаем:

Т а б л и ц а 1.1.

Концентрация	Обозначение концентрации компонента А
в жидкой фазе	в газовой или паровой фазе
Мольная доля,	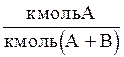x	y
Массовая доля	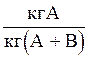`x	`y
Относительная мольная концентрация (доля),	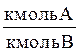X	Y
Относительная массовая концентрация (доля),	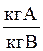`X	`Y
Объемная мольная концентрация,	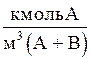С_X	С_y
Объемная массовая концентрация,	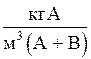`С_X	`С_y

Здесь y*-мольная доля компонента в газовой фазе, равновесной с жидкостью; m=Е/П-безразмерный коэффициент (коэффициент распределения), постоянный для данной системы газ-жидкость при t=const и П=const

Если применительно к двухфазной трехкомпонентной системе (газовая фаза: А+В, жидкая фаза А+С), подставить в уравнение равновесия (1.3) значения x и y* ( для компонента А, выраженные через его относительные концентрации X и Y*, `X и `Y* (табл. 1.2), получим:

; (1.4)

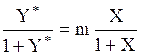
Т а б л и ц а 1.2

Выражение концентрации компонента А	x	`x	X	`X	C_x	`C_x
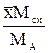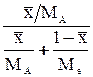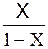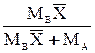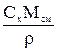x	—	или	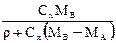		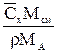или	или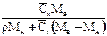
`x		—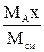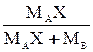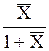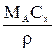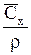
X			—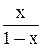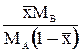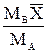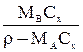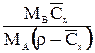
`X				—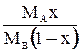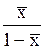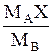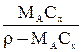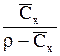
C_x					—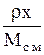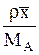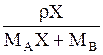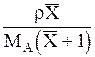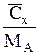
`C_x		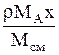r`x		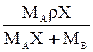	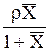М_АС_x	—

М_А, М_В, М_см-мольные массы компонентов и смеси, кг/кмоль; М_см= М_Аx+ М_В(1-x); r-плотность смеси, кг/м 3 . Для смеси идеальных газов: .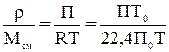

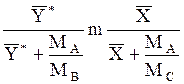
, (1.5)

где М_А— мольная масса распределенного между фазами компонента А; М_В-то же второго компонента бинарной газовой смеси; М_С-то же второго компонента бинарной жидкой смеси.

При малых концентрациях распределенного компонента в газе и в жидкости, когда Y* 2 ; К_y-коэффициент массопередачи, отнесенный к движущей силе Dy, выраженной через мольные доли компонента в газовой фазе, кмоль/(м 2 ×с)** ; К_x — коэффициент массопередачи, отнесенный к движущей силе Dx выраженной через мольные доли компонента в жидкой фазе, кмоль/(м 2 ×с); Dx_ср и Dy_ср-соответствующие средние для всего процесса движущие силы (см. ниже).

В последних уравнениях вместо мольных расходов и концентраций могут быть массовые, а вместо Dy_ср могут быть DY_ср; DСy_ср и Dр_ср; соответственно вместо Dx_ср могут быть DX_ср или DСx_ср.

7.При определенных допущениях (отсутствие диффузионного сопротивления при переходе компонента через поверхность раздела фаз, существование равновесия на этой поверхности, линейность уравнения равновесия y*=mx или y*=mx+b) получаются следующие зависимости между коэффициентами массопередачи К_y и К_x и фазовыми коэффициентами массопередачи b_y и b_x :

; (1.12)

, (1.13)

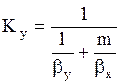
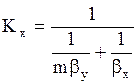
где m-тангенс угла наклона линии равновесия. Коэффициенты массоотдачи и массопередачи выражены в кмоль/(м 2 ×с).

Знаменатели последних уравнений представляют собой общее диффузионное сопротивление, равное сумме диффузионных сопротивлений газовой и жидкой фаз.

Когда основное диффузионное сопротивление сосредоточено в газовой фазе, т. е. при 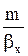2 /с; w-скорость газа или жидкости, м/с; n-кинематический коэффициент вязкости, м 2 /с.

Та б л и ц а 1.3.

Атомный объем, см 3 /атом

Мольный объем, см 3 /моль

В 27,0 С 14,8 Cl 24,6 H 3,7 N в первичных аминах 10,5 N во вторичных аминах 12,0 N с двумя насыщенными связями 15,6 О с двумя насыщенными связями 7,4 О в альдегидах и кетонах 7,4 О в сложных эфирах 9,1 О в простых эфирах 9,9 О в высших простых и сложных эфирах 11,0 О в кислотах 12,0 О в соединениях с S, P, N 8,3 S 25,6

I 37,0 H₂ 14,3 O₂ 25,6 N₂ 31,2 Воздух 29,9 CO 30,7 CO₂ 34,0 SO₂ 44,8 NO 23,6 NO₂ 36,4 NH₃ 25,8 H₂O 18,9 H₂S 32,9 COS 51,5 Cl₂ 48,4 Br₂ 53,2 I₂ 71,5

Бензольное кольцо -15

Нафталиновое кольцо -30

Антраценовое кольцо -47,5

9.При отсутствии экспериментальных данных коэффициент диффузии (молекулярной) газа А в газе В (или газа В в газе А) может быть вычислен по формуле:

, (1.20)

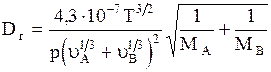
где D_г-коэффициент диффузии, м 2 /с; Т-температура, К; р-давление (абсолютное), кгс/см 2 ; М_А и М_В-мольные массы газов А и В ; u_А и u_В -мольные объемы газов А и В, определяемые как сумма атомных объемов элементов, входящих в состав газа- см. пример 1.6 (атомные объемы некоторых элементов и мольные объемы некоторых газов приведены в табл. 1.3).

Как следует из формулы (1.20), если известно значение коэффициента диффузии D₁ при температуре Т₁ и давлении р₁, то значение его D₂ при температуре Т₂ и давлении р₂ можно найти из уравнения:

. (1.21)

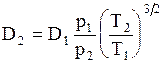
Значения коэффициентов диффузии в воздухе для некоторых газов и паров приведены в табл. XLII.

10.Коэффициент диффузии в жидкости D_ж при 20°С можно вычислить по приближенной формуле:

, (1.22)

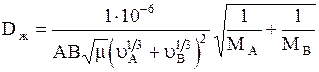
где D_ж— коэффициент диффузии, м 2 /с; m-динамический коэффициент вязкости жидкости, мПа×с; u_А и u_В -мольные объемы растворенного вещества и растворителя; М_А и М_В— мольные массы растворенного вещества и растворителя; А и В -коэффициенты, зависящие от свойств растворенного вещества и растворителя.

Значения коэффициентов А для некоторых веществ, растворенных в воде:

для этилового спирта 1,24

для метилового спирта 1,19

для уксусной кислоты 1,27

Коэффициент В равен:

для этилового спирта 2,0

для метилового спирта 2,0

для ацетона 1,15

для неассоциированных жидкостей 1,0

Коэффициент диффузии газа в жидкости D_t (при температуре t) связан с коэффициентом диффузии D₂₀ (при температуре 20°С) следующей приближенной зависимостью

в которой температурный коэффициент b может быть определен по эмпирической формуле:

, (1.24)

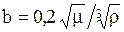
где m-динамический коэффициент вязкости жидкости при 20°С, мПа×с; r-плотность жидкости, кг/м 3 .

Значения коэффициентов диффузии некоторых газов в воде приведены в табл. XLIII.

Коэффициент диффузии в разбавленных растворах может быть вычислен также по формуле:

. (1.25)

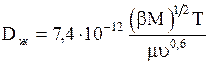
Здесь D_ж— коэффициент диффузии, м 2 /с; М-мольная масса растворителя; u-мольный объем диффузирующего вещества; Т-температура, К; m-динамический коэффициент вязкости растворителя, мПа×с; b-параметр, учитывающий ассоциацию молекул растворителя и равный:

для этилового спирта 1,5

для метилового спирта 1,9

для бензола, эфира, гептана 1

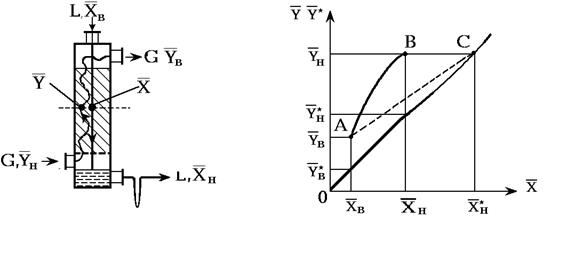
11.Материальный баланс абсорбера (рис. 1.2).

12.

Рис. 1.2 Схема абсорбера.

Рис. 1.3 Рабочая и равновесная линии абсорбера:

АВ — рабочая линия при расходе поглотителя L; АС — рабочая линия при расходе поглотителя L_мин; ОС — равновесная линия Y*=f(`X).

При расчете абсорбера с нелетучим жидким поглотителем массовые (или мольные) расходы поглотителя и инертного, нерастворяющегося в жидкости газа будут постоянными по высоте абсорбера. Выражая концентрации поглощаемого компонента в газе и жидкости в относительных массовых (или мольных) единицах, получим уравнение материального баланса (в массовых единицах):

где М-расход поглощаемого компонента, кг/с; и L- расходы инертного газа и жидкого поглотителя, кг/с; `Y_н и`Y_в — концентрации поглощаемого компонента в газе в низу и на верху абсорбера, кг/кг инертного газа; `X_н и`X_в— то же в жидкости в низу и на верху абсорбера, кг/кг жидкого поглотителя.

В координатах `Y -`X уравнение (1.26), при постоянных G и L, выражает отрезок прямой, проходящей через точки В [`Y_н,`X_н] и А [`Y_в,`X_в] — см. рис. 1.3.

Уравнение этой прямой- рабочей линии:

`Y=`Y_н+ 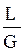(`X-`X_н) (1.27)

`Y=`Y_в+ 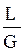(`X-`X_в) (1.28)

где`Y и`X-переменные по высоте колонны концентрации поглощаемого компонента в контактирующих неравновесных потоках газа и жидкости в данном сечении абсорбера — рис. 1.2.

Расход жидкого поглотителя:

Здесь j>1-коэффициент избытка поглотителя; L_мин-теоретически минимальный расход поглотителя, определяемый графическим (см. рис. 1.3) или аналитическим путем:

L_мин= 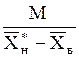. (1.30)

Степенью поглощения (или извлечения) называется величина

с_П= 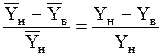. (1.30а)

12.Средняя движущая сила в абсорбере с непрерывным контактом фаз.

В общем уравнении массопередачи

(1.31)

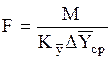
(где F — поверхность массопередачи в абсорбере, м 2 ; М — расход поглощаемого компонента, кг/с; К_`_y — коэффициент массопередачи, 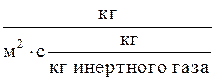) средняя движущая сила D`Y_ср определяется следующим образом.

Если в пределах от `X_в до`X_н (рис. 1.3) линия равновесия прямая, то

, (1.32)

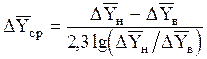
Когда отношение D`Y_н и D`Y_в находятся в пределах

среднюю движущую силу в абсорбере можно рассчитывать по более простой формуле:

Если же линия равновесия не прямая, то

. (1.34)

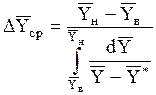
Величину интеграла в знаменателе последнего уравнения находят графическим построением или методом графического интегрирования. Другой метод расчета при криволинейной линии равновесия: разбивают равновесную линию на участки, принимаемые приближенно за отрезки прямых, и для каждого участка в отдельности определяют среднюю движущую силу по уравнению (1.32) или (1.33).

При расчетах абсорберов движущую силу часто выражают в единицах давления — см. пример 1.9.

13.Определение диаметра насадочного абсорбера.

Диаметр абсорбционной колонны D (в м) рассчитывают по уравнению расхода для газового потока:

, (1.35)

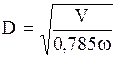
где V — расход газа, проходящего через абсорбер, м 3 /с; w — скорость газа, отнесенная к полному поперечному сечению колонны (фиктивная), м/с.

Скорость газа w находят следующим путем.

Сначала рассчитывают фиктивную скорость газа w₃ в точке захлебывания (инверсии) по уравнению (при r_ж >> r_г):

. (1.36)

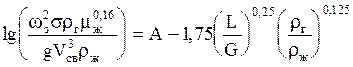
Здесь s-удельная поверхность насадки, м 2 /м 3 ; g-ускорение свободного падения, м/с 2 ; V_св— свободный объем насадки, м 3 /м 3 ; r_г и r_ж— плотности газа и жидкости, кг/м 3 ; m_ж-динамический коэффициент вязкости жидкости, мПа×с; L и G-массовые расходы жидкости и газа, кг/с; А=0,022 для насадки из колец или спиралей* , для ректификации А=-0,125.

Затем определяют рабочую скорость газа w (фиктивную), принимая для абсорберов, работающих в пленочном режиме

14.Определение высоты насадочного абсорбера.

а) Через высоту единицы переноса (ВЕП).

Поверхность контакта фаз в абсорбере при пленочном режиме работы:

где Н_н— высота слоя насадки, м; S=pD 2 /4-площадь поперечного сечения колонны, м 2 ; D-диаметр колонны, м; s-удельная поверхность сухой насадки, м 2 /м 3 ; y-коэффициент смоченности насадки, безразмерный — расчет величины этого коэффициента см.*

Высота слоя насадки:

(1.39)

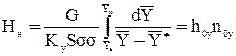
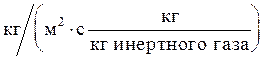
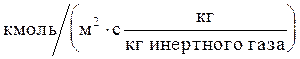
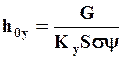
Здесь G — постоянный по высоте колонны расход инертного газа, кг/с или кмоль/с; К_y — средний коэффициент массопередачи, или ; h_0y-высота единицы переноса, м:

; (1.40)

n_0y-общее число единиц переноса:

. (1.40а)

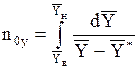
Из уравнения (1.34) следует:

При прямолинейной равновесной зависимости среднюю движущую силу D`Y_ср рассчитывают по уравнению (1.32) или (1.33), при криволинейной равновесной зависимости число единиц переноса n_0y находят графическим построением или методом графического интегрирования-см. пример 1.10.

Объемным коэффициентом массопередачи К_yV называют величину

где а=sj-удельная смоченная (активная) поверхность насадки, м 2 /м 3 ; при y=1 а=s.

Применяя объемный коэффициент массопередачи, получаем для высоты единицы переноса:

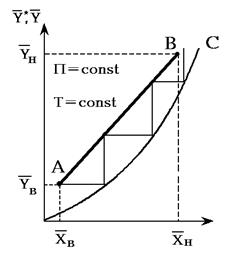
Рис.1.4. Графическое определение числа ступеней изменения концентрации (теоретических тарелок) в абсорбере

. (1.43)

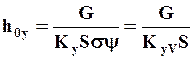
б) Через высоту, эквивалентную теоретической тарелке (ВЭТТ).

Высота слоя насадки Н_н может быть рассчитана также по уравнению:

где h_э — высота, эквивалентная теоретической тарелке (ВЭТТ) или теоретической ступени (ВЭТС), м (определяется по экспериментальным данным); n_т — число теоретических тарелок (ступеней изменения концентрации).

Число теоретических тарелок-ступеней изменения концентрации в абсорбере определяют обычно графическим путем (рис. 1.4). На этом рисунке АВ — рабочая линия, построенная по уравнению (1.27) или (1.28), ОС — равновесная линия.

15.Критериальные формулы для расчета коэффициентов массоотдачи в насадочных абсорберах с неупорядоченной насадкой (навалом) при пленочном режиме.

а) Для газовой фазы:

. (1.45)

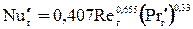
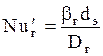
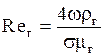
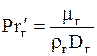
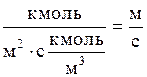
Здесь ; ; ; b_г— коэффициент массоотдачи для газа, ; D_г— коэффициент диффузии поглощаемого компонента в газе, м 2 /с. Остальные обозначения — см. формулы (1.36) и (1.38).

Уравнение (1.45) справедливо при значениях Re_г от 10 до 10 000.

б) Для жидкой фазы:

, (1.46)

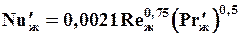
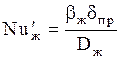
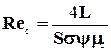
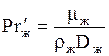
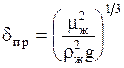
где ; ; ; b_ж — коэффициент массоотдачи для жидкости, м/с; -так называемая приведенная толщина жидкой пленки, м; D_ж— коэффициент диффузии поглощаемого компонента в жидкости, м 2 /с; L — массовый расход жидкости, кг/с.

Выражение для критерия Re_ж получено следующим путем.

Обозначения-см. уравнения (1.36) и (1.38).

Омываемый жидкостью периметр сечения абсорбера находим из уравнения (1.38):

Скорость течения пленки жидкости через насадку:

, (1.48)

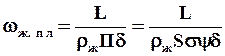
где d — средняя толщина пленки, м.

Эквивалентный диаметр жидкой пленки:

Подставляя эти значения в выражение для критерия Re_ж, получаем:

. (1.50)

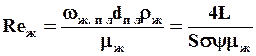
16.Определение диаметра и высоты тарельчатой абсорбционной колонны проводится так же, как и для тарельчатых ректификационных колонн-см. гл. 2. Диаметр тарельчатого абсорбера рассчитывают по уравнениям (2.16) и (2.17). Высоту тарельчатой части абсорбера Н_т определяют по уравнению (2.18). Требуемое число тарелок находят графически с применением кинетических зависимостей для расчета коэффициентов массопередачи или ВЕП. При приближенных расчетах для определения числа тарелок находят графически число ступеней изменения концентрации (рис. 1.4) и затем число тарелок n по уравнению (2.19).

Примеры

Пример 1.1.Жидкая смесь содержит 58,8% (мол.) толуола и 41,2% (мол.) четыреххлористого углерода (ч. х. у.). Определить относительную массовую концентрацию толуола `X (в кг толуола/кг ч. х. у.) и его объемную массовую концентрацию `С_x (в кг/м 3 ).

Р е ш е н и е . Относительная массовая концентрация толуола:

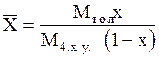
где М_тол— мольная масса толуола (92 кг/кмоль); М_ч.х.у.— то же четыреххлористого углерода (154 кг/кмоль); x — мольная доля толуола.

кг толуола/кг ч. х. у.

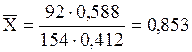
Чтобы рассчитать объемную массовую концентрацию толуола `С_x, необходимо знать плотность смеси r_см. Для расчета плотности предварительно найдем массовую долю толуола `x.

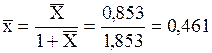
Далее по табл. IV находим: плотность толуола r_тол=870 кг/м 3 , плотность четыреххлористого углерода r_ч.х.у.=1630 кг/м 3 .

Считая, что изменение объема при смешении не происходит, т. е. объем смеси равен сумме объемов компонентов, находим объем одного кг смеси

м 3 ,

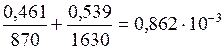
откуда плотность смеси:

кг/м 3 .

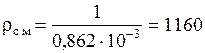
Можно рассчитать r_см и так:

кг/м 3 .

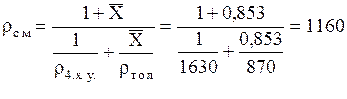
Объемная массовая концентрация толуола:

Пример 1.2.Воздух атмосферного давления при температуре 34°С насыщен водяным паром. Определить парциальное давление воздуха, объемный и массовый % пара в воздушно-паровой смеси и его относительную массовую концентрацию, считая оба компонента смеси идеальными газами. Атмосферное давление 745 мм рт. ст. Определить также плотность воздушно-паровой смеси, сравнить ее с плотностью сухого воздуха.

Р е ш е н и е. По табл XXXVIII находим, что при t= 34°C давление насыщенного водяного пара составляет 39,9 мм рт. ст. Это давление является парциальным давлением водяного пара р_п в воздушно-паровой смеси, а парциальное давление воздуха равняется:

Мольная (объемная) доля водяного пара в меси:

Массовая доля пара:

Относительная массовая концентрация

кг пара/кг воздуха.

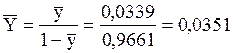
Плотность воздушно-паровой смеси рассчитываем как сумму плотностей компонентов, взятых каждая при своем парциальном давлении:

= =(29×705+18×39,9)=1,105 кг/м 3 .

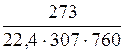
Можно рассчитать плотность смеси иначе.

Мольная масса смеси:

Плотность смеси при П=745 мм рт. ст. и t=34°C:

кг/м 3

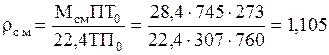
Плотность сухого воздуха при тех же давлении и температуре:

кг/м 3 .

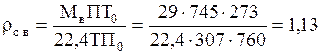
Пример 1.3. При температуре 25°С приведены в соприкосновение: воздух атмосферного давления, содержащий 14% (об.) ацетилена (С₂Н₂), и вода, содержащая растворенный ацетилен в количестве: а) 0,29×10 -3 кг на 1 кг воды; б) 0,153×10 -3 кг на 1 кг воды. Определить: 1) из какой фазы в какую будет переходить ацетилен; 2) движущую силу этого процесса перехода в начальный момент времени (в относительных мольных концентрациях). Атмосферное давление 765 мм рт. ст. Равновесные концентрации ацетилена в газовой и в жидкой фазах определяются законом Генри.

Р е ш е н и е . Закон Генри [уравнение (1.2)]:

По табл, XLI находим, что при t=25°С коэффициент Генри Е=1,01×10 6 мм рт. ст.

Парциальное давление ацетилена в воздухе по уравнению (1.1):

p=yП=0,14×765=107 мм рт. ст.

а) Мольная доля ацетилена в воде при `X=0,29×10 -3 кг ацетилена/кг воды (табл. 1.2):

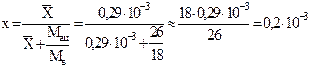
Ответы на вопросы примера могут быть получены двумя путями.

I. В условиях равновесия парциальное давление ацетилена в газовой фазе над жидкостью с x=0,2×10 -3 по закону Генри должно составлять:

p*=Еx=1,01×10 6 ×0,2×10 -3 =202 мм рт. ст.

Имеющееся в действительности над этой жидкостью парциальное давление ацетилена меньше: p=107 мм рт. ст. Чтобы в процессе массопередачи система газ-жидкость приближалась к состоянию равновесия, парциальное давление ацетилена в газовой фазе должно увеличиваться, т. е. он будет переходить из воды в воздух.

Движущая сила этого процесса перехода (отклонение от состояния равновесия) в начальный момент времени будет равна: в единицах парциального давления ацетилена

Dp=p*-p=202-107=95 мм рт. ст.

в мольных долях

Dy=y*-y= 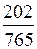-0,14=0,264-0,14=0,124;

в относительных мольных концентрациях

=0,359-0,163=0,196 кмоль ацетилена/кмоль воздуха.

II. В условиях равновесия с газовой фазой, в которой парциальное давление ацетилена равняется 107 мм рт. ст., вода по закону Генри должна иметь концентрацию ацетилена (в мольных долях):

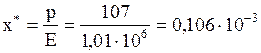
Имеющаяся в действительности мольная доля ацетилена в воде больше: x=0,2×10 -3 . Для того чтобы в процессе массоперехода система приближалась к состоянию равновесия, мольная доля ацетилена в воде должна уменьшаться, т. е. ацетилен будет переходить из воды в воздух.

Движущая сила этого процесса перехода в начальный момент времени (считая ее по концентрации в жидкой фазе):

в мольных долях

Dx=x-x*=0,2×10 -3 -0,106×10 -3 =0,094×10 -3 ;

в относительных мольных концентрациях

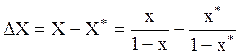
Так как в данном примере x и х* оба много меньше единицы, то в знаменателях последнего уравнения ими можно пренебречь и

DX=x-x*=0,094×10 -3 кмоль ацетилена/кмоль воды.

б) Мольная доля ацетилена в воде:

х » 18×0,153×10 -3 /26=0,106×10 -3 .

Перехода ацетилена из одной фазы в другую не будет, так как соприкасающееся фазы находятся в равновесии:

x=x*=0,106×10 -3 , y=y*=0,14.

Пример 1.4. В массообменном аппарате, работающем под давлением р_абс=3,1 кнс/см 2 , коэффициенты массоотдачи имеют следующие значения: b_y=1,07 кмоль/м 2 ×ч(Dy=1), b_x=22 кмоль/м 2 ×ч(Dx=1). Равновесные составы газовой и жидкой фаз характеризуются законом Генри р*=0,08×10 6 x. Определить: а) коэффициенты массопередачи К_у и К_х; б) во сколько раз диффузионное сопротивление жидкой фазы отличается от диффузионного сопротивления газовой фазы:

Источник