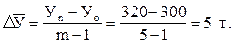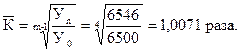Способы выравнивания рядов динамик

Способы выравнивания рядов динамик

• Укрупнение периодов — применяется, когда явление в интервальном ряду выражено в абсолютных величинах, уровни которых суммируются по более крупным периодам. Применение возможно при кратном числе периодов.
• Вычисление групповой средней — применяется, когда уровни интервального ряда выражены в абсолютных, средних или относительных величинах, которые суммируются, а затем делятся на число слагаемых. Способ применяется при кратном числе периодов.
• Расчет скользящей средней — применяется, когда уровни явлений любого ряда выражены в абсолютных, средних или относительных величинах. Данный метод применяется при наличии некратного числа временных периодов (7, 11, 13, 17, 19) достаточно длинного динамического ряда. Путем вычисления групповой средней значений 3 периодов, а в последующем переходя на определенный уровень и два соседних с ним, осуществляется «скольжение» по периодам. Каждый уровень заменяется на среднюю величину (из данного уровня и двух соседних с ним). Данный метод применяется, когда не требуется особой точности, когда имеется достаточно длинный ряд и можно пренебречь потерей двух значений ряда; в случаях, когда изучается развитие явления под влиянием одного или двух факторов.
• Метод наименьших квадратов применяется для более точной количественной оценки динамики изучаемого явления. Этим способом получаются такие выровненные значения уровней ряда, квадраты отклонений которых от истинных (эмпирических) показателей дают наименьшую сумму.

Наиболее простой и часто встречающейся в практике является линейная зависимость, описываемая уравнением:

У_х = а + вХ, либо У_{теоретич.} = У_{среднее} + вХ,

где У_х — теоретические (расчетные) уровни ряда за каждый период;
а — среднеарифметический показатель уровня ряда, рассчитывается по формуле:
а = ΣУ_факт. / n;
в — параметр прямой, коэффициент, показывающий различие между теоретическими уровнями ряда за смежные периоды, определяется путем расчета по формуле: в = Σ(ХУ_факт)/ ΣХ 2
где n — число уровней динамического ряда;
X — временные точки, натуральные числа, проставляемые от середины (центра) ряда в оба конца.

При наличии нечетного ряда уровень, занимающий срединное положение, принимается за 0. Например, при 9 уровнях ряда: -4, -3, -2, -1, 0, +1, +2, +3, +4.

При четном числе уровней ряда две величины, занимающие срединное положение, обозначаются через -1 и +1, а все остальные — через 2 интервала. Например, при 6 уровнях ряда: -5, -3, -1, +1, +3, +5.

Расчеты проводят в следующей последовательности:

1. Представляют фактические уровни динамического ряда (У_ф) (см. табл.).
2. Суммируют фактические уровни ряда и получают сумму У_факт.
3. Находят условные (теоретические) временные точки ряда X, чтобы их сумма (ΣХ) была равна 0.
4. Возводят теоретические временные точки в квадрат и суммируют их, получая ЕX 2 .
5. Рассчитывают произведение Х на У и суммируют, получая ΣХУ.
6. Рассчитывают параметры прямой:
   а = ΣУ_факт / n в = Σ(Х У_факт) / ΣX 2
7. Подставляя последовательно в уравнение У_х = а + аУ значения X, находят выровненные уровни У_х.

Для углубленного изучения процессов во времени рассчитывают показатели динамического ряда.

1. Для характеристики скорости изменения процесса применяются такие показатели, как абсолютный прирост (убыль), темп прироста (убыли).
   • Абсолютный прирост (убыль) характеризует скорость изменения процесса (абсолютную величину прироста (убыли) в единицу времени). Абсолютный прирост рассчитывается как разность между данным уровнем и предыдущим; обозначается знаком «+», характеризуя прирост, или знаком «—», характеризуя убыль.
   • Темп прироста (убыли) характеризует величину прироста (убыли) в относительных показателях в % и определяется как процентное отношение абсолютного прироста (убыли) к предыдущему уровню ряда; обозначается знаком «+» (прирост) или знаком «—» (убыль).

Для характеристики изменения процесса одного периода по отношению к предыдущему периоду применяется такой показатель, как темп роста (снижения); рассчитывается как процентное отношение последующего (уровня) к предыдущему.

При сравнении динамических рядов с разными исходными уровнями (например, средними, интенсивными, абсолютными) используется показатель — значение 1% прироста (убыли); рассчитывается как отношение абсолютного прироста к темпу прироста за каждый период.

Для обобщенной количественной оценки тенденций динамического ряда используется показатель, именуемый средним темпом прироста (снижения), выраженный в %. При его расчете для большинства рядов можно использовать следующую формулу:

где К = 1 при нечетном числе уровней ряда; К = 2 при четном числе уровней ряда;
а и в — показатели линейной зависимости, используемые при выравнивании ряда методом наименьших квадратов.

Условие задачи: В Н-ском районе изучена заболеваемость населения ветряной оспой за 10 лет (см. табл.).

Таблица. Заболеваемость населения Н-ского района ветряной оспой за 10 лет (на 10 000 населения)

Годы	1997	1998	1999	2000	2001	2002	2003	2004	2005	2006
Показатель	3,5	4,9	3,6	5,7	6,5	5,5	8,1	7,2	5,0	7,3

Задание: на основании данного динамического ряда требуется:

1. Обосновать необходимость выравнивания ряда.
2. Выровнять ряд по способу наименьших квадратов.
3. Рассчитать показатели динамического ряда (абсолютный прирост, темп прироста, средний темп прироста, значение 1% прироста).
4. Изобразить ряд графически.
5. Сделать выводы о динамике явления по выровненным уровням.
6. Охарактеризовать скорость изменения заболеваемости.

Годы	Выравнивание по способу наименьших квадратов					Показатели динамического ряда
	Уф факт. уровни	Х времен. точки	X 2	XУ	Уx выровнен. уровни	абс. прирост	темп прироста, %	средний темп прироста	среднее значение 1% прироста
1997	3,5	-9	81	-31,5	4,119	—	—	Tпр.сн.= ((вхК)/a) х 100 = ((0,179 х 2 / 5,73) x 100 = 6,24%	+0,358 / 6,24 = +0,057
1998	4,9	-7	49	-34,3	4,477	+0,358	8,69
1999	3,6	-5	25	-18	4,835	7,99
2000	5,7	-3	9	-17	5,193	7,4
2001	6,5	-1	1	-6,5	5,551	6,89
2002	5,5	+1	1	+5,5	5,909	6,44
2003	8,1	+3	9	+24,3	6,267	6,05
2004	7,2	+5	25	+36,0	6,625	5,7
2005	5,0	+7	49	+35	6,983	5,4
2006	7,3	+9	81	+65,7	7,341	5,1
n=10	Σ УФ = 57,3	Σ Х = 0	Σ Х 2 = 330	ΣХУ= 59,1	ΣУx = 57,3

Заболеваемость населения Н-ского района
ветряной оспой за 10 лет (на 10 000 населения)

а = ΣУ_ф. / n = 57,3 / 10 = 5,73
УХ ₉₇ = 5,73 + 0,179 х (-9) = 4,119
в = Σ(Х У_факт) / σ X 2 = 59,2 / 330 = 0,179
УХ ₉₇ = 5,73 + 0,179 х (-9) = 4,119
УХ ₉₈ = 5,73 + 0,179 х (-7) = 4,477
УХ ₉₉ = 5,73 + 0,179 х (-5) = 4,835

Абсолютный прирост выровненного ряда — 4,477-4,119 = 0,358
Темп прироста для 1997 г. = (0,358 / 4,119) х 100 = 8,69%
Темп прироста для 1998 г. = (0,358 / 4,477) х 100 = 7,99%
Темп прироста для 1999 г. = (0,358 / 4,835) х 100 = 7,4%
Средний темп прироста = (0,179 х 2 / 5,73) х 100 = 6,24%
Абсолютный прирост = 4,477 — 4,119 = + 0,358
Значение 1% прироста = + 0,358 / 6,24 = 0,057%.

Выводы. Заболеваемость населения Н-ского района ветряной оспой за 10 лет неравномерна. Скорость изменений показателей заболеваемости различна, наибольший темп прироста отмечается в 1998 г. При выравнивании показателей динамического ряда отмечается тенденция к увеличению уровней заболеваемости, в среднем на 6,24% ежегодно.

Применение методов статистического анализа для изучения общественного здоровья и здравоохранения. Под ред. чл.-корр. РАМН, проф. В.З.Кучеренко. М., «Гэотар-Медиа», 2007, учебное пособие для вузов

1. Власов В.В. Эпидемиология. — М.: ГЭОТАР-МЕД, 2004. — 464.
2. Лисицын Ю.П. Общественное здоровье и здравоохранение. Учебник для вузов. — М.: ГЭОТАР-Медиа, 2007. — 512 с.
3. Медик В.А., Юрьев В.К. Курс лекций по общественному здоровью и здравоохранению: Часть 1. Общественное здоровье. — М.: Медицина, 2003. — 368 с.
4. Социальная медицина и организация здравоохранения (Руководство в 2 томах). Миняев В.А., Вишняков Н.И. и др. — СПб, 1998. — 528 с.
5. Социальная гигиена и организация здравоохранения (Учебное пособие). Кучеренко В.З., Агарков Н.М. и др. — Москва, 2000. — 432 с.

Источник

Приемы выравнивания динамических рядов

Для выявления временных закономерностей требуется, как правило, достаточно большое число уровней динамического ряда. Если же динамический ряд состоит из ограниченного числа уровней, то его выравнивание можно провести с помощью средних показателей динамики: абсолютного прироста, коэффициента (темпа) роста и др.

Применение того или другого способа выравнивания ряда базируются на изучении характера (типа) динамики. Так, если фактические уровни динамического ряда характеризуются более-менее стабильными (положительными или отрицательными) абсолютными приростами и на координатной диаграмме они равномерно отклоняются от теоретической прямой линии, то выравнивание уровней может проводиться по среднему абсолютному приросту, т.е.

(9.18)

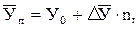
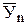
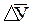
где – выравниваемый искомый уровень; У₀ – начальный (базисный) уровень; – средний абсолютный прирост уровней ряда; n – порядковый номер искомого (выравниваемого) уровня.

Применение этого способа выравнивания динамического ряда покажем на следующем примере. Допустим, имеются данные о выпуске длинного льноволокна в перерабатывающей организации за пятилетие, т: 2006г. – 300, 2007г. – 280, 2008г. – 310, 2009г. – 290, 2010г. – 320.

Этот динамический ряд необходимо выровнять по среднему абсолютному приросту, т.е. найти теоретические уровни, которые могли быть достигнуты при условии равномерного динамического развития.

Прежде всего найдем среднегодовой абсолютный прирост производства льноволокна за пятилетие:

Поскольку начальный (базисный) уровень ряда известен по условию, а средний абсолютный прирост уровней составляет 5 т, можно рассчитать все искомые (выравниваемые) уровни за каждый год динамического ряда по формуле (9.18):

2006 г. – У₀=У₀+ 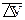· n=300+5 · 0=300 т; 2009 г. – У₃=300+5 · 3=315 т;

2007 г. – У₁=300+5 · 1=305 т; 2010 г. – У₄=300+5 · 4=320 т.

2008 г. – У₂=300+5 · 2=310 т;

Недостаток выравнивания динамического ряда по среднему абсолютному приросту заключаются в том, что этот способ базируется на значениях начального и конечного уровней, а промежуточные уровни в процессе выравнивания не участвует и, следовательно, не оказывают влияния на выровненные уровни динамического ряда.

В тех случаях, когда изучаемый динамический ряд характеризуется более-менее стабильными повышающимися или снижающимися темпами роста, выравнивание уровней такого ряда можно проводить с помощью среднего коэффициента(темпа) роста:

(9.19)

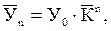
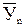
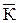
где – выравниваемый искомый уровень; У₀ – начальный уровень ряда; – средний коэффициент роста уровней; n – порядковый номер выравниваемого уровня.

Предположим, необходимо выровнять динамический ряд годового удоя одной коровы в сельскохозяйственной организации «Днепр» за пятилетие по следующим данным, кг: 2006г. – 6500, 2007г. – 6600, 2008г. – 6400, 2009г. – 6500, 2010г. – 6546.

По этим данным прежде всего рассчитаем среднегодовой коэффициент роста уровней за пятилетний период:

Далее подставим необходимые данные в формулу (9.19) и найдем искомые выровненные уровни динамического ряда:

2006 г. – У₀= 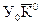=6500 · (1,0071) 0 =6500 кг;

2007 г. – У₁=6500 · (1,0071) 1 =6546 кг;

2008 г. – У₂=6500 · (1,0071) 2 =6593 кг;

2009 г. – У₃=6500 · (1,0071) 3 =6639 кг;

2010 г. – У₄=6500 · (1,0071) 4 =6686 кг.

Основной недостаток этого способа выравнивания динамического ряда состоит в том, что он базируются только на начальном и конечном уровнях; промежуточные же уровни используются в процессе предварительного анализа ряда для оценки характера (типа) динамики.

Источник