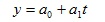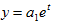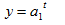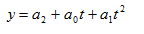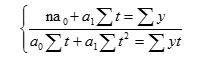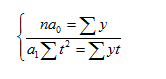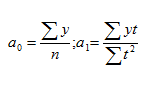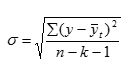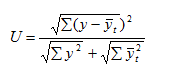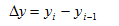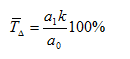Способы выравнивания динамического ряда тест

Динамические ряды — краткое руководство по анализу изменений явлений во времени

Даная статья понятными и простыми терминами объяснит, что же такое динамические ряды, для чего они нужны, как производится анализ полученных данных и какие возможности открываются перед теми, кто владеет методикой данного анализа. Любое явление в области здравоохранения нуждается в тщательной оценке, и здесь знания анализа динамических рядов неоценимы. С помощью динамического ряда можно оценить и спрогнозировать проблематику любой нозологической единицы, сформировать дальнейшую тактику лечения и меры профилактики заболеваний.

Динамический ряд — ряд однородных величин, характеризующих изменение явления во времени.

Целью анализа динамических рядов является:

• выявление закономерности изменения изучаемого явления во времени;
• прогнозирование (экстраполирование) полученных данных на последующие
  годы.

Числовые значения, составляющие динамический ряд, называются уровнями ряда (у).

Типы динамических рядов:

1. В зависимости от вида уровня ряда:

а) простые (уровень ряда выражен абсолютными числами);

б) сложные (уровень ряда выражен обобщающими коэффициентами).

1. В зависимости от способа формирования временного интервала:

а) моментные (данные собираются на определенный момент времени);

б) интервальные (данные собираются за определенный период времени).

1. В зависимости от выраженности изменений явления во времени (определя­ется по коэффициенту корреляции между временем и изучаемым явлением).

а) с выраженной тенденцией (r =0,7 — 1,0);

б) с неустойчивой тенденцией (r =0,3 — 0,69);

в) с отсутствием тенденции ( r = 0 — 0,29).

Основное требование, предъявляемое к анализируемым динамическим ря­дам, заключается в сопоставимости их уровней. Для оценки сопоставимости прово­дят предварительный анализ полученных данных по следующим критериям:

• единство территории, на которой проводился сбор данных;
• единая методология учета данных;
• единые временные интервалы, в течение которых проводилась регистрация
  данных.

Методика анализа динамических рядов

Методика аналитики предусматривает выполнение последовательных действий:

1. Представить полученные данные графически и выявить форму зависимости изучаемого явления от времени.
2. Оценить наличие и силу корреляции изучаемого явления от времени.
3. Если установлено, что ряд обладает выраженной тенденцией, проводят анализ компонентов динамики ряда: основной тенденции (эволюции, тренда), кратковременных систематических движений и случайных колебаний. Основная задача анализа — разделить эти компоненты и выявить основную закономерность изменения явления во времени. Для выявления и описания тренда динамический ряд подвергают обработке — выравниванию.

Способы выравнивания динамических рядов

Чтобы произвести выравнивание динамических рядов потребуются следующие действия:

• Укрупнение временных интервалов (периодов), в течение которых изучается явление.
• Сглаживание ряда методом скользящей средней.
• Аналитический способ.

При этом способе на основании фактических данных подбирается наиболее подходящее для отражения тенденции развития явления математическое уравнение (аппроксимирующая функция), которое принимается за модель развития явления во времени. Т.е. уровни ряда рассматриваются как функция времени, и задача выравнивания сводится к определению вида функции, отысканию ее параметров по эмпирическим данным и расчету по найденной формуле теоретических выравненных уровней. Наиболее часто используются следующие функции:

а) линейная зависимость:

б) экспоненциальная зависимость:

в) показательная зависимость:

г) параболическая зависимость:

у – теоретический уровень;

t – временной интервал.

В качестве примера возьмем линейную зависимость и проведем выравнивание, используя для нахождения параметров уравнения а₀ ,а₁ способ наименьших квадратов. Способ наименьших квадратов позволяет найти теоретическую кривую, максимально приближенную к эмпирической, а условие минимума суммы квадратов отклонений теоретических данных от фактических позволяет свести математическое решение задачи к системе нормальных уравнений:

где у — уровни фактического ряда;

n — количество уровней;

t — порядковый номер временного периода.

Эта система уравнений легко упрощается, если «t» присвоить ранги (порядковые номера), ведя отсчет времени от середины ряда. При нечетном ряде середина обозначается через 0, а отсчет рангов ведется через единицу с соответствующим знаком в ту или иную сторону от середины (например: -5,-4,-3,-2,-1, 0,+1.+2,+3,->:4,+5). При четном ряде две средние временные точки обозначаются через +1 и -1, а остальные ранги присваиваются через две единицы (например: -5,-3,-1,+1,+3,+5).

При отсчете времени от середины ряда St = 0 и система нормальных уравнений принимает вид:

Отсюда находим параметры уравнения:

Подставляя в уравнение у = а₀ + а₁t вместо «t» его ранги, находим выравненные (теоретические) значения уровней ряда и строим теоретическую кривую выравненного динамического ряда.

При использовании аналитического способа всегда отмечается отклонение теоретических уровней от фактических уровней ряда, которое может быть обуслов­лено как случайными колебаниями, так и неправильно подобранным аппроксими­рующим уравнением. В связи с этим заключительным этапом выравнивания динамического ряда аналитическим способом является оценка точности аппроксимации с определенным уровнем значимости.

Оценка точности аппроксимации возможна с помощью нахождения

Для получения точной оценки необходимо найти такие величины:

а) коэффициент вариации:

где у- фактический уровень ряда;

y_t — теоретический уровень ряда;

k- число параметров уравнения;

n- число уровней ряда.

Аппроксимация считается точной при C_v не более 15%.

б) коэффициент расхождения Тейла:

где у — фактический уровень ряда;

y_t — теоретический уровень ряда.

Аппроксимация считается точной при U не более 5%

После аналитического выравнивания динамического ряда и описания тренда возможно экстраполировать полученные данные. Экстраполяция — предположение о сохранении тренда, базирующееся на допущении неизменности влияющих факто­ров и предшествующей тенденции. Осуществляется путем подставления в найденное уравнение аппроксимации не фактического значения временного интервала, а предполагаемого порядкового номера (ранг) того периода, на который прогнозируется результат.

Вычисление основных показателей динамического ряда

Алгоритм вычислений ведущих параметров динамических рядов:

yi- текущий уровень (сравниваемый);

у_i-1— базисный уровень (с каким сравнивают);

t- период времени, в течение которого уровень предполагается неизменным.

1.Абсолютный прирост (убыль) :

2.Темп роста (убыли):

3.Темп прироста (относительная скорость), темп убыли :

4.Средний темп прироста (убыли):

где а₀; а₁ — параметры уравнения;

k = 1 при нечетном ряде;

k = 2 при четном ряде.

5.1% прироста (убыли): используются при сравнении динамических рядов с уровнями, выраженными различными обобщающими коэффициентами.

Таким образом, с помощью данного руководства по определению и расчетам такого понятия, как, динамические ряды, специалисты различных отраслей медицины, ученые могут эффективно и быстро оценить изменение различных величин в течение времени.

Благодарим за интерес, проявленный к нашей статье, оставайтесь с нами!

Источник

Статистика. Ряды динамики.

Список вопросов теста

Вопрос 1

Ряд динамики характеризует:

Варианты ответов

• структуру совокупности по какому-либо признаку
• изменение значений признака во времени
• определение значений варьирующего признака в совокупности
• факторы изменения показателя на определенную дату или за определенный период

Вопрос 2

Абсолютный прирост в рядах динамики исчисляется как …. уровней ряда

Варианты ответов

• разность
• сумма
• произведение
• частное

Вопрос 3

В зависимости от времени, к которому относится динамический ряд различают:

Варианты ответов

• моментные динамические ряды
• сложносоставные динамические ряды
• динамические ряды с абсолютными величинами
• детерминированные динамические ряды
• интервальные динамические ряды

Вопрос 4

Чем отличаются темпы прироста от темпов роста?

Варианты ответов

• Темп роста равен темпу прироста
• Темп прироста равен темп роста минус единица (или, если в %, то минус 100%)
• Темп роста всегда выше темпа прироста
• Темп прироста равен темп роста плюс единица (или, если в %, то плюс 100%)

Вопрос 5

Чем различаются базисные и цепные темпы роста и прироста?

Варианты ответов

• Базисные — рассчитываются отношением значения максимального показателя к минимальному, а цепные – как отношение минимальных значений к значению показателя, принятого за базу
• Базисные — рассчитываются отношением нового значения к предыдущему, а цепные – как отношение новых значений к значению показателя, принятого за базу
• Базисные — рассчитываются отношением значения минимального показателя к максимальному, а цепные – как отношение максимальных значений к значению показателя, принятого за базу
• Базисные — рассчитываются отношением нового значения к базовому – (первому значению ряда), а цепные – как отношение новых значений к предыдущему значению показателя

Вопрос 6

Рассчитайте темп роста (в %) по представленным показателям:
отчётный год — 780 тыс. рублей;
предыдущий год — 710 тыс. рублей

Варианты ответов

Вопрос 7

Что характеризует среднехронологическая:

Варианты ответов

• среднюю величину между соотношениями генеральной совокупности
• среднюю величину между частями генеральной совокупности
• среднюю величину уровня явления за изучаемый период
• среднюю величину между отдельными проявлениями явления

Вопрос 8

Определить средний уровень динамического ряда:

Годы	Объем производства, млн.р.
2015	10
2016	12
2017	11
2018	12
2019	9

Варианты ответов

• 9 млн. руб.
• 90 %
• 10,8 млн. руб.
• 12 млн. руб.

Вопрос 9

Что показывает формула темпа роста

Варианты ответов

• На сколько процентов данный уровень больше (или меньше) другого, принимаемого за базу сравнения
• Сколько процентов составил рост статистического показателя текущего периода в сравнении с другим, принятым за базу сравнения
• Средний уровень ряда

Вопрос 10

Определить среднегодовой темп прироста:

Годы	Объем производства, млн.р.
2015	15,2
2016	17,5
2017	15,5
2018	12,9
2019	17,1

Варианты ответов

Вопрос 11

Интервальный динамический ряд — это ряд, в котором время задано…

Варианты ответов

• в виде промежутков — лет, месяцев, суток
• в виде конкретных дат
• как разница между началом и концом отчетного периода
• в виде постоянного момента времени

Вопрос 12

Что показывает формула темпа прироста?

Варианты ответов

• Средний уровень ряда
• Сколько процентов составил рост статистического показателя текущего периода в сравнении с другим, принятым за базу сравнения
• На сколько процентов данный уровень больше (или меньше) другого, принимаемого за базу сравнения

Вопрос 13

Определить среднегодовой темп роста:

Годы	Объем производства, млн.р.
2015	7
2016	6
2017	8
2018	7
2019	6

Варианты ответов

Вопрос 14

Абсолютное значение 1% прироста равно:

Варианты ответов

• уровню ряда, взятому за базу сравнения, деленному на 100
• абсолютному приросту, деленному на темп прироста
• абсолютному приросту, деленному на темп роста
• уровню ряда, деленному на темп прироста

Вопрос 15

За два анализируемых периода времени темп роста объемов производства продукции составил 110%. Это означает…

Источник