- Способы вычисления поверхностного интеграла 2 рода
- Вычисление поверхностных интегралов: теория и примеры
- Понятие поверхностного интеграла первого рода
- Вычисление поверхностного интеграла первого рода
- Понятие поверхностного интеграла второго рода
- Вычисление поверхностного интеграла второго рода
- Больше примеров на вычисление поверхностных интегралов
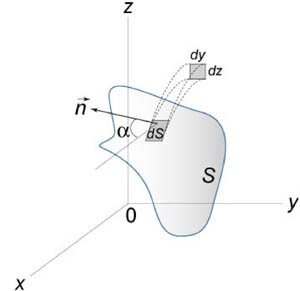
Способы вычисления поверхностного интеграла 2 рода
Обозначим через \(\mathbf
Если \(S\) является границей ограниченной области, то ее можно ориентировать внешней или внутренней нормалями. Поверхность \(S,\) ориентированную внешней нормалью, называют ее внешней стороной , а ориентированную внутренней нормалью, − ее внутренней стороной .
Поверхностный интеграл второго рода от векторного поля \(\mathbf
Если поверхность \(S\) ориентирована внешней нормалью (\(k\)-компонент вектора нормали является положительным), то \[ <\iint\limits_S <\mathbf> > = <\iint\limits_S <\mathbf
Если поверхность \(S\) ориентирована внутренней нормалью (\(k\)-компонент вектора нормали является отрицательным), то \[ <\iint\limits_S <\mathbf> > = <\iint\limits_S <\mathbf
Поверхностный интеграл второго рода можно записать также в координатной форме . Пусть \(P\left(
Если поверхность \(S\) не представима в явном или параметрическом виде, то ее можно попробовать разбить на конечное число частей, каждая из которых представима в таком виде. В этом случае справедливо свойство аддитивности: поверхностный интеграл второго рода по поверхности \(S\) будет равен сумме интегралов по ее частям.
Источник
Вычисление поверхностных интегралов: теория и примеры
Понятие поверхностного интеграла первого рода
Поверхностный интеграл — обобщение понятия криволинейного интеграла на случаи, когда интегрирование происходит не по отрезку кривой, а по ограниченной поверхности. Как и криволинейные интегралы, поверхностные интегралы бывают первого рода и второго рода.
Поверхностный интеграл первого рода записывается в виде

где f(M) = f(x,y,z) – функция трёх переменных, а поверхность σ — область интегрирования этой функции. Если f(x,y,z) равна единице, то поверхностный интеграл равен площади поверхности.
Представьте себе довольно большой подсолнух с очень-очень маленькими семечками. Тогда по сумме поверхностей очень-очень маленьких семечек, расположенных на поверхности подсолнуха, можно вычислить поверхность подсолнуха — таким может быть упрощённое толкование поверхностного интеграла. Почему так?
Давайте перейдём к более формальному определению поверхностного интеграла. Поверхность σ разбита на n частей с площадями Δσ 1 , Δσ 2 , . Δσ n . Если выбрать на каждой частичной поверхности (семечке) произвольную точку M i с координатами (ζ i , η i , ς i ,) , то можно составить сумму

Эта сумма называется интегральной суммой для функции f(M) по поверхности σ . Теперь будем максимально увеличивать число таких маленьких частей, а наибольший диаметр Δσ i — наоборот, уменьшать. Если интегральная сумма при стремлении наибольшего из диаметров частей к нулю (то есть, как мы уже отмечали, все части очень маленькие) имеет предел, то этот предел и называется поверхностным интегралом первого рода от функции f(M) по поверхности σ .
Вычисление поверхностного интеграла первого рода
Вычисление поверхностного интеграла первого рода производится сводением к двойному интегралу.
Пусть поверхность σ задана уравнением z = z(x, y) , её проекцией на плоскость xOy является область D xy , при этом функция z = z(x, y) и её частные производные 

Это и есть формула, выражающая поверхностный интеграл первого рода через двойной интеграл по проекции поверхности σ на плоскость xOy.
Пример 1. Вычислить поверхностный интеграл первого рода
где σ — часть плоскости 
Из уравнения плоскости получаем выражение «зет»: 
Тогда частные производные: 


Поверхность σ является изображённым на чертеже треугольником ABC , а его проекцией на плоскость xOy — треугольником AOB , который ограничен прямыми x = 0 , y = 0 и 3x + y = 6 . От поверхностного интеграла перейдём к двойному интегралу и решим его:

Понятие поверхностного интеграла второго рода
Прежде чем перейти к определению поверхностного интеграла второго рода, требуется познакомиться с понятиями стороны поверхностей и ориентированных поверхностей.
Пусть в пространстве дана гладкая поверхность σ. На этой поверхности выберем произвольную точку M и проведём через неё вектор нормали 
Если направление вектора нормали не поменяется, то поверхность σ называется двусторонней. Если же при обходе контура направление вектора нормали поменяется на противоположное, то поверхность называется односторонней. Двусторонние поверхности называются ориентированными поверхностями, односторонние — неориентированными поверхностями.
Пример односторонней поверхности — лист Мёбиуса (на рисунке выше), который можно сделать из полоски бумаги, одна сторона которой повёрнута на 180 градусов, и затем концы склеены. И вот что здесь важно: для односторонней поверхности понятие поверхностного интеграла второго рода не вводится.
Так что будем рассматривать только двусторонние поверхности. Примеры двусторонних поверхностей — плоскости, сфера, эллипсоил, параболоид.
Положительную сторону двустороней поверхности определяет направление вектора нормали. Противоположная сторона поверхности называется отрицательной. Положительной стороной поверхности называется её верхняя сторона. Если единичные векторы нормали составляют острые углы с осью Oz, то выбрана верхняя сторона поверхности z = z(x, y) , если углы тупые, то нижняя сторона поверхности.
Как и в случае поверхностного интеграла первого рода, поверхность можно разбить на n частей. При формулировке понятия поверхностного интеграла первого рода в интегральной сумме присутствовали площади каждой из частей, на которые умножаются значения функции f(M i ) . В случае поверхностного интеграла второго рода берутся площади не самих частей, а площади их проекций на координатные плоскости. А функцию трёх переменных для отличия от интеграла первого рода обозначим R(x,y,z) . Тогда интегральная сумма запишется так:

где Δs i — площади упомянутых проекций частей стороны поверхности на координатную ось (пока будем считать, что на ось xOy).
При таких соглашениях и обозначениях определение поверхностного интеграла второго рода аналогично определению интеграла первого рода. А именно: поверхностным интегралом второго рода называется предел данной интегральной суммы при стремлении к нулю наибольшего из диаметров частей рассматриваемой поверхности.
Записывается он так:

В данном случае функция R(x,y,z) интегрируема по переменным x и y, так как части поверхности проецировались на плоскость xOy.
Аналогично можно записать и два других поверхностных интеграла второго рода:
(функция P(x,y,z) интегрируема по переменным y и z, так как части поверхности проецируются на плоскость yOz),
(функция Q(x,y,z) интегрируема по переменным z и x, так как части поверхности проецируются на плоскость zOx).
Сумма этих интегралов
называется общим поверхностным интегралом второго рода и обозначается
Вычисление поверхностного интеграла второго рода
Поверхностный интеграл второго рода вычисляется путём разложения общего поверхностного интеграла второго рода на сумму поверхностных интегралов (см. окончание предыдущего параграфа) и сведением каждого из них к двойному интегралу.
Рассмотрим подробно вычисление интеграла

Пусть поверхность σ задана уравнением z = z(x, y) . Положительную сторону поверхности обозначим 

Таким образом, получаем формулу для вычисления поверхностного интеграла второго рода:

Если выбрана отрицательная сторона поверхности, то знак интеграла меняется:

Аналогично вычисляются два других отдельных интеграла — слагаемых общего:


Пример 2. Вычислить поверхностный интеграл второго рода

где σ — верхняя сторона части плоскости 
Решение. Чертёж — на рисунке сверху. По определению получаем сумму трёх двойных интегралов:
Второй интеграл равен нулю, так как плоскость σ параллельна оси Oy . Поэтому найдём первый и третий интегралы:
Остаётся лишь сложить все отдельные интегралы и получить общий поверхностный интеграл второго рода:

Если требуется вычислить поверхностный интеграл второго рода по замкнутой поверхности, можно перейти к тройному интегралу, используя формулу Остроградского. Тогда, если функции P(x,y,z) , Q(x,y,z) и R(x,y,z) и их частные производные 


Пример 3. Вычислить поверхностный интеграл второго рода

где σ — внешняя сторона поверхности конуса, образованного поверхностью 
Решение. Данная поверхность является поверхностью конуса с радиусом R = 2 и высотой h = 2 . Это замкнутая поверхность, поэтому можно использовать формулу Остроградского. Так как P = 3x , Q = 4y , R = −z , то частные производные 


Переходим к тройному интегралу, который и решаем:
Больше примеров на вычисление поверхностных интегралов
Пример 4. Вычислить поверхностный интеграл первого рода

где σ — боковая поверхность конуса 

Решение. Так как частные производные 

Сводим данный поверхностный интеграл к двойному:

Проекцией поверхности на плоскость xOy является круг с центром в начале координат и радиусом R = 2 , поэтому при вычислении двойного интеграла перейдём к полярной системе координат. Для этого сделаем замену переменных:
Получаем следующий интеграл, который окончательно и решаем:
Пример 5. Вычислить поверхностный интеграл второго рода

где σ — верхняя часть треугольника, образованного пересечением плоскости 
Решение. Данный поверхностный интеграл разделим на сумму двух интегралов



Чтобы вычислить интеграл I 1 , построим проекцию поверхности σ на плоскость yOz. Проекцией является треугольник OCB , который на плоскости yOz ограничивают прямые 


Чтобы вычислить интеграл I 2 , построим проекцию поверхности σ на плоскость zOx. Проекцией является треугольник AOC , который ограничивают прямые 

Складываем два полученных интеграла и окончательно получаем данный поверхностный интеграл:

Пример 6. Вычислить поверхностный интеграл второго рода

где σ — внешняя поверхность пирамиды, образованной плоскостью 
Решение. Данный поверхностный интеграл вычислим двумя способами
1) интегрируя по каждой грани пирамиды;
2) используя формулу Остроградского.
1) Вычисление интегрированием по каждой грани пирамиды.
а) Вычислим интеграл по треугольнику ABC . Для этого разделим интеграл на сумму трёх интегралов, которые отдельно решим:

Складываем и получаем:

б) Вычислим поверхностный интеграл по треугольнику AOB , который находится в плоскости z = 0 . Тогда dz = 0 и, учитывая, что нормальный вектор плоскости образует с осью Oz тупой угол, получаем
в) Треугольник AOC находится в плоскости y = 0 , таким образом, dy = 0 и (нормальный вектор плоскости образует с осью Oy тупой угол) получаем
г) Осталось вычислить поверхностный интеграл по треугольнику CBO находится в плоскости x = 0 , таким образом, dx = 0 и получаем

В результате получаем данный поверхностный интеграл второго рода:

2) Используя формулу Остроградского, от поверхностного интеграла по замкнутой поверхности перейдём к тройному интегралу, где W — область, ограниченная поверхностью σ . Так как P = xz , Q = 1 , R = 2y , то частные производные 


Получаем следующее решение данного поверхностного интеграла:
В последнем примере вернёмся к вычислению поверхностного интеграла первого рода.
Пример 7. Вычислить площадь поверхности параболоида 

Решение. Определим, при каком значении z данные поверхности пересекаются:
Значение −3 не подходит, поэтому остаётся только z = 1 .
Обозначим через C часть поверхности данного параболоида во внутреней стороне сферы. Проекция поверхности C (обозначим её D ) на плоскость xOy является кругом с центром в начале координат и радиусом √2 , так как при z = 1 получаем уравнение окружности 


Проекцией поверхности на плоскость xOy является круг, поэтому при вычислении двойного интеграла перейдём к полярной системе координат. Для этого сделаем замену переменных:
Получаем окончательное решение данного поверхностного интеграла:
Источник