Способы вычисления погрешностей при прямых измерениях

Способы вычисления погрешностей при прямых измерениях

Погрешности прямых измерений. Промах. Систематическая погрешность. Случайная погрешность. Полная погрешность. Погрешности косвенных измерений. Запись результата измерений

1. Оценка погрешности прямых измерений

Измерить физическую величину – это значит сравнить ее с однородной величиной, принятой за единицу меры.

Различают прямые и косвенные измерения.

Если измеряемая величина непосредственно сравнивается с мерой, то измерения называются прямыми. Например, измерения линейных размеров тел с помощью масштабной линейки и т.д.

Если измеряется не сама искомая величина, а некоторые другие величины, связанные с ней функциональной зависимостью, то измерения называются косвенными. Например, измерения объема, ускорения и т.д.

Из-за несовершенства средств и методик измерения, органов чувств при любом измерении неизбежны отклонения результатов измерений от истинных величин. Эти отклонения называются погрешностями измерений.

Погрешности измерений делятся на систематические, случайные и промахи.

1.1. Промахи, связанные с неправильными отсчетами по прибору, неправильными записями и т.д., приводят к очень большой по абсолютной величине погрешности. Они, как правило, не укладываются в общую закономерность измеренных величин. Обнаруженный промах следует отбросить.

1.2. Систематическими погрешностями Δx_сист называются погрешности, которые сохраняются при повторных измерениях одной и той же величины x или изменяются по определенному закону.

Систематические погрешности подразделяются на несколько групп. Отметим только приборную погрешность.

Систематическая приборная погрешность определяется по классу точности прибора, который указывается на приборе следующими цифрами: 0,01; 0,02; 0,05; 1,0; 2,5; 4,0. Класс точности показывает предельно допустимое значение систематической погрешности, выраженной в процентах от верхнего предела на выбранном диапазоне измерений. Например, предел измерения вольтметра с классом точности 0,5 равен 200 В. Систематическая погрешность равна 0,5% от 200В. Следовательно, систематическая погрешность вольтметра равна 1 В.

Если на приборе класс точности не указан, то погрешность равна половине цены наименьшего деления шкалы прибора.

1.3. Случайными называются погрешности, которые изменяются беспорядочно при повторных измерениях одной и той же физической величины при одинаковых условиях.

Оценим случайную погрешность. Пусть при измерении какой-либо физической величины было произведено N измерений и были получены значения x₁, x₂, … x_N. Тогда наиболее вероятным значением измеряемой величины является ее среднее арифметическое значение

Результаты измерений x₁, x₂, … x_N «рассеиваются» вокруг среднего. В качестве меры «рассеяния» результатов наблюдения вокруг среднего служит среднее квадратичное отклонение

Пусть a будет истинным, но неизвестным значением измеряемой величины x. Доказано, что вероятность попадания результатов измерения величины x в интервал значений от (a – S) до (a + S) оказывается равной α = 0,68.

Вероятность попадания результатов наблюдений в более широкие интервалы (a – 2S, a + 2S) и (a – 3S, a + 3S) равна α = 0,95 и α = 0,99 соответственно.

Вероятность попадания в заданный интервал значений величины x называется доверительной вероятностью, а сам интервал – доверительным интервалом.

Однако, таким образом полученный доверительный интервал справедлив при большом значении N. В учебных лабораториях, как правило, приходится ограничиваться небольшим числом измерений. В этом случае доверительный интервал находят с помощью коэффициента Стьюдента, который зависит от числа измерений N и доверительной вероятности α. В таблице 1 приведены коэффициенты Стьюдента для различного числа наблюдений при доверительных вероятностях α = 0,68; 0,95; 0,99.

Источник

4. Методика расчета погрешностей измерений. Погрешности прямых измерений

При обработке результатов прямых измерений рекомендуется принять следующий порядок выполнение операций.

Проводятся измерения заданного физического параметра n раз в одинаковых условиях,и результаты записываются в таблицу.

Если результаты некоторых измерений резко отличаются по своему значению от остальных измерений, то они как промахи отбрасываются, если после проверки не подтверждаются.

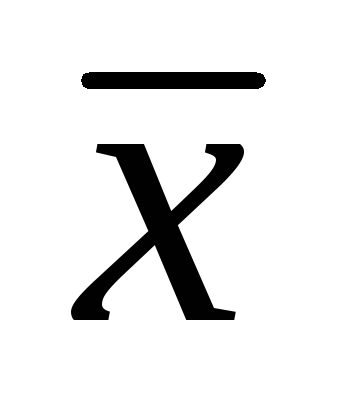
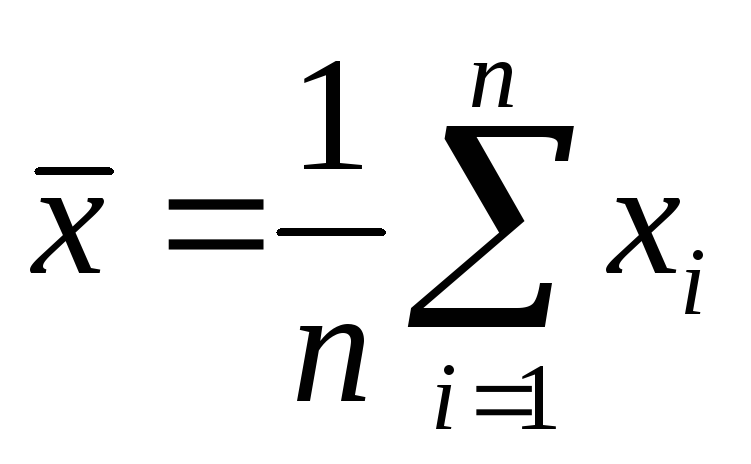
Вычисляется среднее арифметическое изnодинаковых измерений. Оно принимается за наиболее вероятное значение измеряемой величины

. (8)

Находятся абсолютные погрешности отдельных измерений

Вычисляются квадраты абсолютных погрешностей отдельных измерений (Δх_i) 2

Определяется средняя квадратичная ошибка среднего арифметического

.

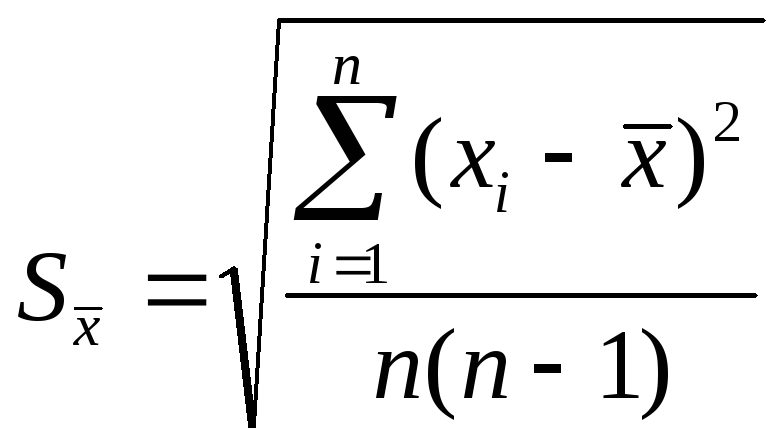
Задается значение доверительной вероятности α. В лабораториях практикума принято задаватьα=0,95.

Находится коэффициент Стьюдента для заданной доверительной вероятности α и числа произведенных измерений (см.табл.)

Определяется случайная погрешность

.

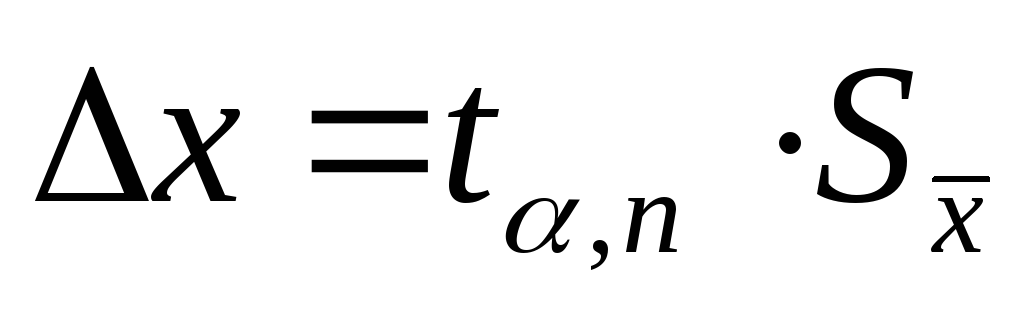
Определяется суммарная погрешность

.

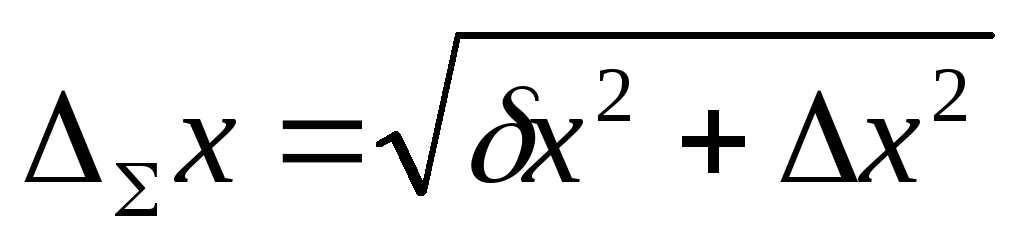
Оценивается относительная погрешность результата измерений

.

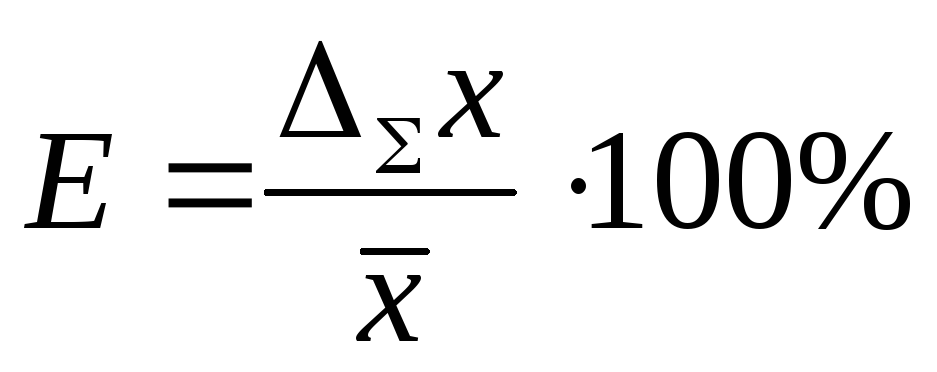
Записывается окончательный результат в виде

, с α=… Е=…%.

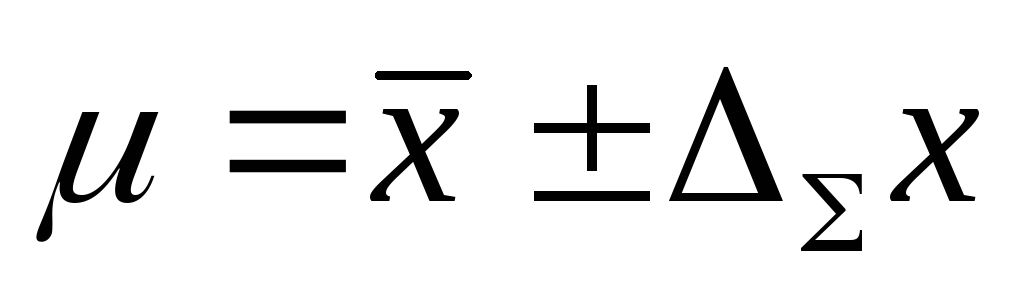
5. Погрешность косвенных измерений

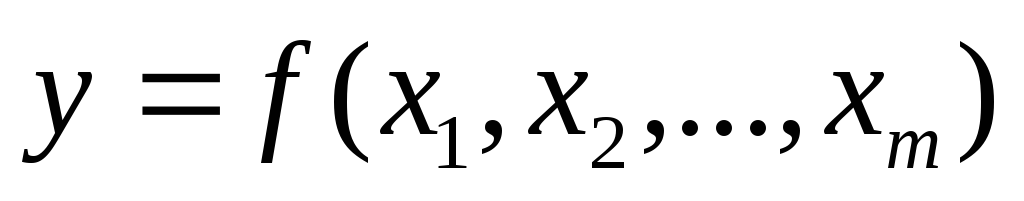
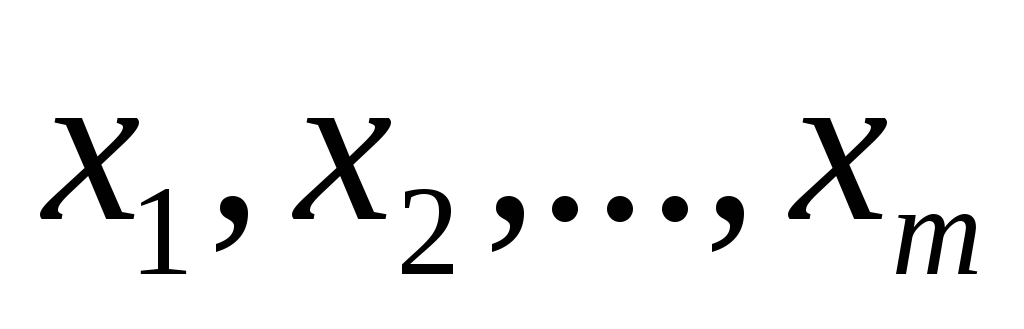
При оценке истинного значения косвенно измеряемой величины , являющейся функцией других независимых величин, можно использовать два способа.

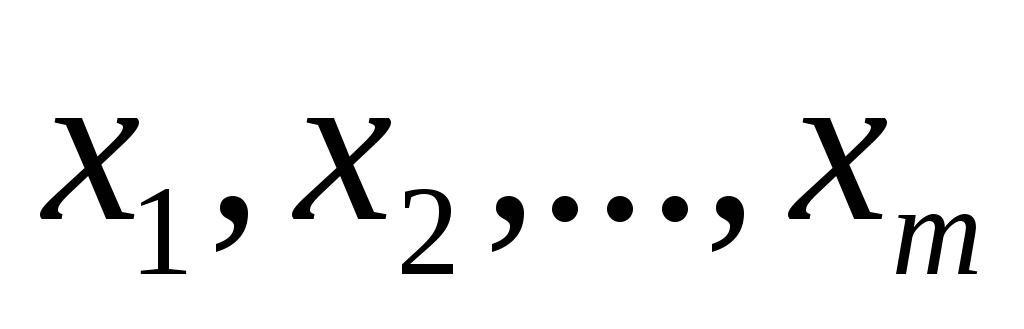
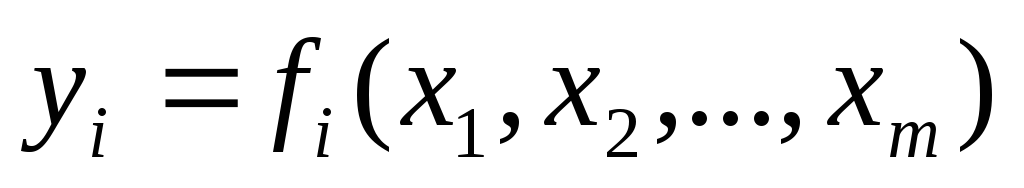
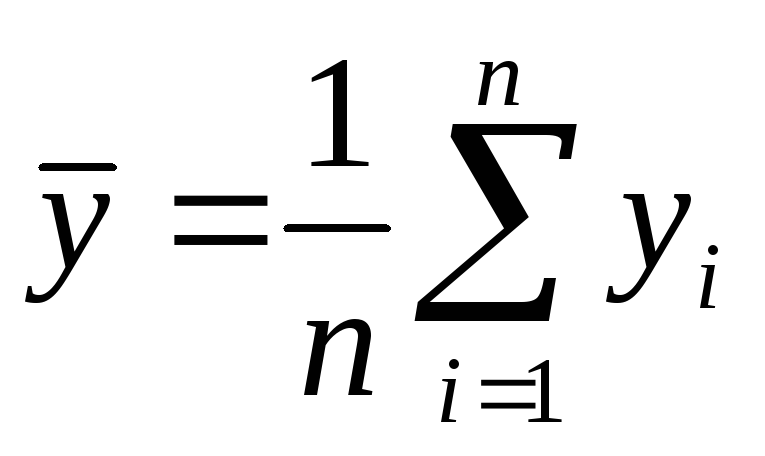
Первый способ используется, если величинаyопределяется при различных условиях опыта. В этом случае для каждого из значенийвычисляется, а затем определяется среднее арифметическое из всех значенийy_i

. (9)

Систематическая (приборная) погрешность находится на основании известных приборных погрешностей всех измерений по формуле. Случайная погрешность в этом случае определяется как ошибка прямого измерения.

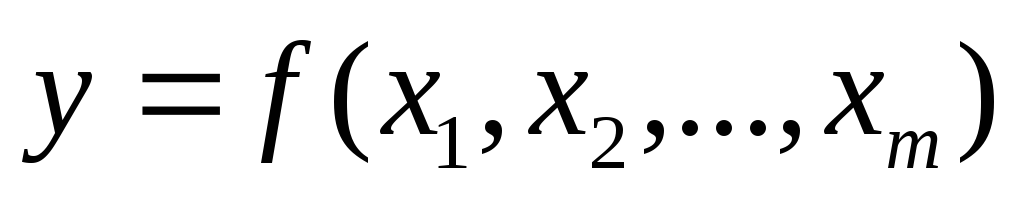
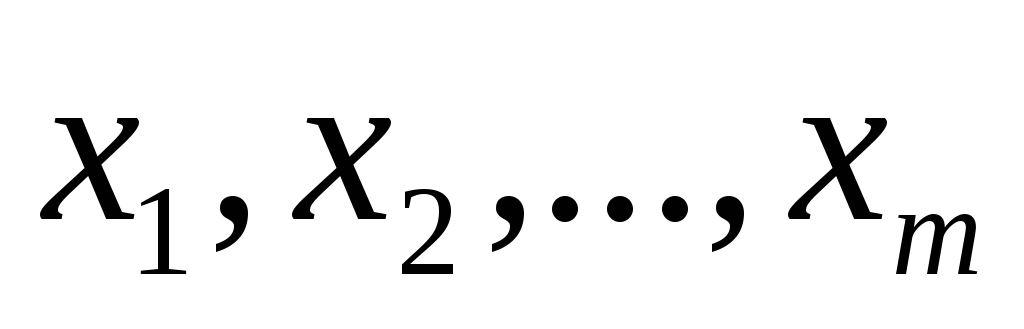
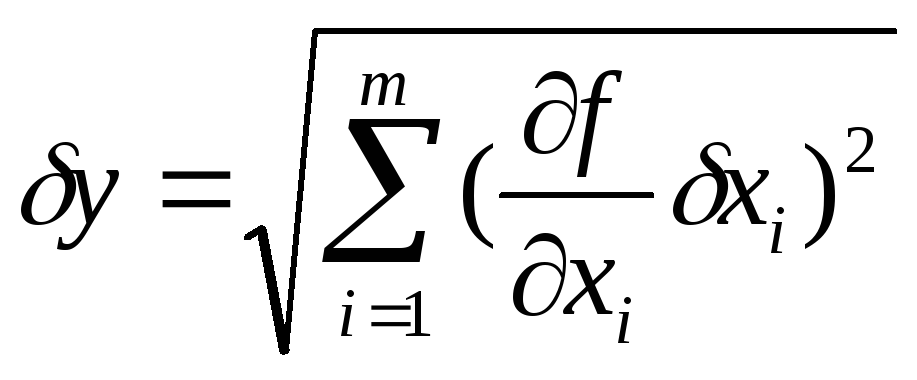
Второй способ применяется, если данная функцияy определяется несколько раз при одних и тех же измерений. В этом случае величинарассчитывается по средним значениям. В нашем лабораторном практикуме чаще используется второй способ определения косвенно измеряемой величиныy.Систематическая (приборная) погрешность, как и при первом способе, находится на основании известных приборных погрешностей всех измерений по формуле

. (10)

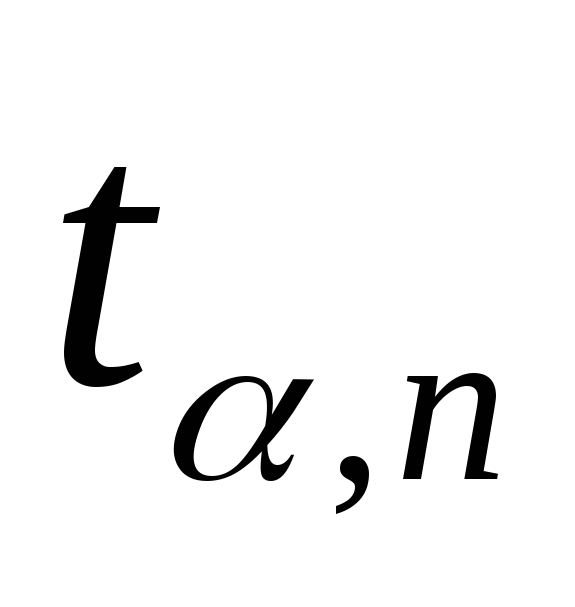
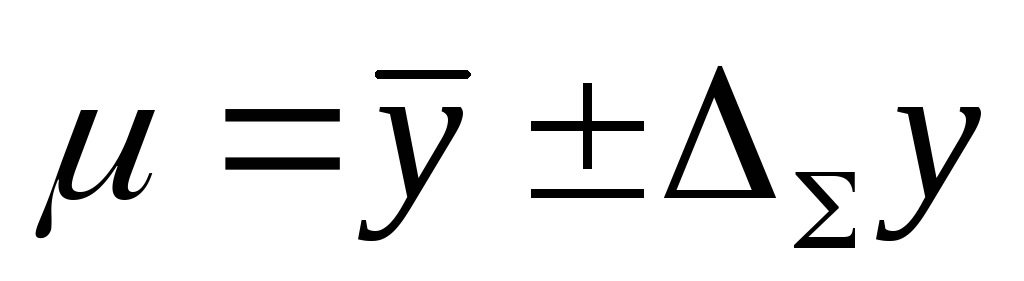
Для нахождения случайной погрешности косвенного измерения вначале рассчитываются средние квадратичные ошибки среднего арифметического отдельных измерений. Затем находится средняя квадратичная ошибка величины y.Задание доверительной вероятностиα, нахождение коэффициента Стьюдента, определение случайной и суммарной ошибок осуществляются так же, как и в случае прямых измерений. Аналогичным образом представляется результат всех расчетов в виде

, сα=… Е=…%.

6. Пример оформления лабораторной работы

Лабораторная работа №1

ОПРЕДЕЛЕНИЕ ОБЪЕМА ЦИЛИНДРА

Принадлежности:штангенциркуль с ценой деления 0,05 мм, микрометр с ценой деления 0,01 мм, цилиндрическое тело.

Цель работы:ознакомление с простейшими физическими измерениями, определение объема цилиндра, расчет погрешностей прямых и косвенных измерений.

Источник

Расчет погрешностей при прямых измерениях

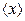
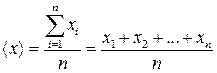
Допустим, что мы проводим серию из n измерений одной и той же величины х. Из-за наличия случайных ошибок отдельные значения х₁, х₂, х_3, х_n неодинаковы, и в качестве наилучшего значения искомой величины выбирается среднее арифметическое , равное арифметической сумме всех измеренных значений, деленной на число измерений:

. (П.1)

где å – знак суммы, i – номер измерения, n – число измерений.

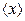
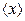
Итак, – значение, наиболее близкое к истинному. Истинного же значения никто не знает. Можно лишь рассчитать интервал Dх вблизи , в котором истинное значение может находиться с некоторой степенью вероятности р. Этот интервал называется доверительным интервалом. Вероятность, с которой истинное значение в него попадает, называется доверительной вероятностью, или коэффициентом надежности (так как знание доверительной вероятности позволяет оценить степь надежности полученного результата). При расчете доверительного интервала необходимая степень надежности задается заранее. Она определяется практическими потребностями (например, к деталям мотора самолета предъявляются более жесткие требования, чем к лодочному мотору). Очевидно, для получения большей надежности требуется увеличение числа измерений и их тщательности.

Благодаря тому, что случайные погрешности отдельных измерений 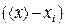подчиняются вероятностным закономерностям, методы математической статистики и теории вероятностей позволяют рассчитать среднюю квадратичную погрешность среднего арифметического значения Dх_сл. Запишем без доказательства формулу для расчета Dх_сл при малом числе измерений (n

Так как каждое из значений х_i получено с погрешностью d, то полный доверительный интервал Dх, или абсолютную погрешность измерения, рассчитывают по формуле:

. (П.3)

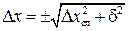
Заметим, что если в формуле (П.3) одна из величин хотя бы в 3 раза больше другой, то меньшей пренебрегают.

Абсолютная погрешность сама по себе не отражает качества проведенных измерений. Например, только по информации абсолютная погрешность равна 0,002 м² нельзя судить о том, сколь хорошо было проведено данное измерение. Представление о качестве проведенных измерений дает относительная погрешность e, равная отношению абсолютной погрешности к среднему значению измеряемой величины. Относительная погрешность показывает, какую долю составляет абсолютная погрешность от измеренного значения. Как правило, относительную погрешность выражают в процентах:

100 %. (П.4)

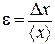
Рассмотрим пример. Пусть диаметр шара 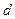измеряется с помощью микрометра, инструментальная погрешность которого d = 0,01 мм. В результате трех измерений получились следующие значения диаметра:

По формуле (П.1) определяют среднее арифметическое значение диаметра шара

мм.

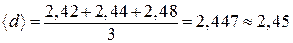
Затем по таблице коэффициентов Стьюдента находят, что для доверительной вероятности 0,68 при трех измерениях t_n,p = 1,3. После чего по формуле (П.2) рассчитывают случайную погрешность измерения Dd_сл

мм.

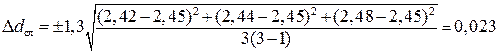
Так как полученная случайная погрешность всего в два раза превышает приборную погрешность, то при нахождении абсолютной погрешности измерения Dd по (П.3) следует учитывать и случайную погрешность, и погрешность прибора, т. е.

мм » ±0,03 мм.

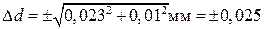
Погрешность округлили до сотых миллиметра, так как точность результата не может превышать точность измерительного прибора, которая в данном случае составляет 0,01 мм.

Итак, диаметр проволоки равен

мм.

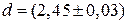
Данная запись говорит о том, что истинное значение диаметра шара с вероятностью 68 % лежит в интервале (2,42 ¸ 2,48) мм.

Относительная погрешность e полученного значения согласно (П.4) составляет

%.

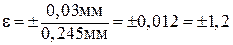
Источник