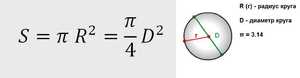Способы вычисления площади сечения

Метод сечений в стереометрии

Из опыта работы школы N 759 Северо-Восточного учебного округа г. Москвы за 1990-1997 гг.

Курс стереометрии общеобразовательной школы по программе, рассчитанной на два урока в неделю, страдает в своей практической части недостаточной преемственностью курса планиметрии, слабой взаимосвязью с другими учебными предметами и не является в полной мере составной частью базы знаний, необходимых учащимся для продолжения образования в высших учебных заведениях.

Метод сечений, широко известный своей универсальностью, применяется в некоторых разделах физики, в теоретической механике, сопротивлении материалов, гидравлике, в некоторых разделах высшей математики и других естественных науках и технических дисциплинах высшего образования. Этот метод оказывает значительное влияние на развитие у учащихся пространственных представлений и пространственного мышления.

Данный материал характеризуется следующими особенностями:

1. Метод сечений применяется только для многогранников, так как различные сложные (наклонные) виды сечений тел вращения не входят в программу средней школы.

2. В задачах используются в основном простейшие многогранники — с целью доступности решения таких задач как учащимися, так и учителями, а также ввиду возможности применения одних и тех же геометрических конструкций по нескольку раз для изучения различных тем.

3. Учителям, знакомящимся с данным материалом, предлагается самим оценить уровень его трудности в соответствии с уровнем подготовки своих учащихся. Материал как полностью, так и частично, может быть полезен классам и школам всех типов, в том числе и классам с углубленным изучением математики.

4. Задачи представлены в основном без числовых данных, чтобы создать возможность их многовариантного применения. В некоторых задачах намеренно повторяются алгоритмы вычисления различных элементов с целью упрочнения умений и навыков учащихся и стандартизации подхода к решению предложенных и аналогичных задач.

Материал расположен в той последовательности, в какой он применялся для обучения учащихся. Классифицировать его по тематике задач с примерным соблюдением принципа «от простого к сложному» можно весьма условно следующим образом:

I. Нахождение площади сечений в многогранниках (до изучения теоремы о площади ортогональной проекции многоугольника).
II. Использование свойств подобных треугольников.
III. Нахождение расстояния и угла между скрещивающимися прямыми в многогранниках.
IV. Определение угла между плоскостями.
V. Нахождение площади сечений в многогранниках (с применением теоремы о площади ортогональной проекции многоугольника).
VI. Отношение объемов частей многогранника.
VII. Наибольшее и наименьшее значения площади переменного сечения в многогранниках.
VIII. Вращение многогранников.

Применение метода сечений в практической части большинства тем стереометрии подтверждает его универсальность.

Нахождение площади сечений в многогранниках

(до изучения теоремы о площади ортогональной проекции многоугольника)

Источник

Расчет площади поперечного сечения круга

В инженерной и строительной практике нередко встречаются задачи по расчёту площади поперечного сечения. Если фигуру разрезать по линии, которая перпендикулярна продольной оси предмета, то полученный торец и будет поперечным сечением. Круг — один из наиболее часто встречающихся видов подобного рассечения. Такой срез присущ цилиндру, шару, конусу, тору, эллипсоиду.

Определение величины

Площадь — это величина, характеризующая размер геометрической фигуры. Её определение — одна из древнейших практических задач. Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на высоту.

По прошествии долгих лет трудом многих мыслителей был выработан математический аппарат для расчета этой величины практически для любой фигуры.

На Руси существовали особые единицы измерения: копна, соха, короб, верёвка, десятина, четь и другие, так или иначе связанные с пахотой. Две последних получили наибольшее распространение. Однако от древнерусских землемеров нам досталось только само слово — «площадь».

С развитием науки и техники появилось не только множество формул для расчёта площадей любых геометрических фигур, но и приборы, которые делают это за человека. Такие приборы называют планиметрами.

Область применения

Круг — одна из фундаментальных фигур, которые окружают человека повсюду. Трубы, колеса, лампы, конфорки у плиты — всё это имеет форму круга или поперечное сечение в виде круга. Расчёт площади такого сечения может понадобиться в следующих ситуациях:

1. Определение объемов емкостей.
2. Решение задач по сопротивлению материалов и электротехнике.
3. Расчет количества материалов при проектировании, строительстве и ремонте.
4. Ведение поливного земледелия.

Стоит обратить внимание на разницу между кругом и окружностью. Окружность — это замкнутая кривая, все точки которой равно удалены от центра, в то время как круг — это часть плоскости (геометрическая фигура), ограниченная окружностью.

Круг имеет ряд характеристик:

• радиус (r/R) — отрезок, соединяющий центр фигуры с его границей;
• диаметр (d/D) — отрезок, который соединяет две точки границы круга и проходит через его центр;
• длина окружности (C/c/L/l).

Теорема гласит: площадь круга (S) равна произведению половины длины окружности и его радиуса. Длина окружности С находится в прямой зависимости от радиуса R с коэффициентом π («пи» = 3,14).

Способы расчета

Чтобы получить круглое поперечное сечение, необходимо разрезать объёмную фигуру перпендикулярно оси вращения. В случае с цилиндром площади всех поперечных сечений будут равны между собой — как, например, кружки колбасы, нарезанные поперек батона, одинаковы.

Шар, по сути, представляет собой напластование блинчиков-кругов различного диаметра от точечного до заданного и обратно до точки. Чтобы найти S какого-либо из блинчиков, необходимо определить его радиус. Принцип его расчёта сводится к решению теоремы Пифагора, где гипотенузой выступает радиус шара, а искомый радиус становится одним из катетов.

При расчёте площади сечений конуса необходимо найти радиус или диаметр каждого из кругов, учитывая, что в продольном разрезе конус — это равнобедренный треугольник.

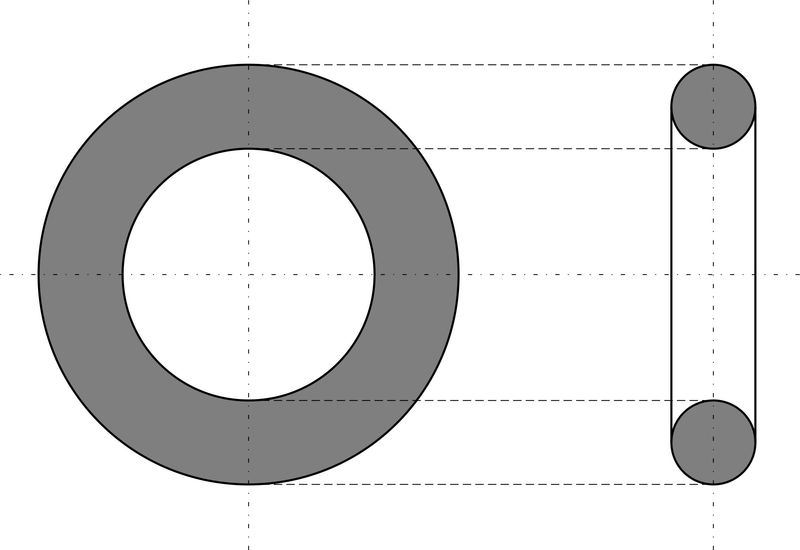
Цилиндр, конус и шар — базовые объемные фигуры. Однако существуют более сложные фигуры, например, тор. Тор, или тороид, при первом приближении являет собой не что иное, как бублик или баранку. Разломив его пополам, на торцах можно увидеть два одинаковых круга. Площадь такого поперечного сечения можно получить, удвоив имеющуюся (на рисунке серая область справа). Если взять нож и рассечь баранку вдоль, на срезе получится кольцо. В случае с такой фигурой необходимо найти площадь круга по внешней окружности и вычесть из нее «дырку от бублика» (показано серым на рисунке слева).

Площадь круглого поперечного сечения рассчитывается исходя из имеющихся характеристик. Она сводится к трем основным формулам. Их можно представить таким образом:

1. Самая популярная, легкая в применении и часто используемая формула. Чтобы узнать площадь фигуры, если известен её радиус, нужно возвести это значение в квадрат и умножить на число π. Для бытовых расчетов достаточно двух знаков после запятой, то есть π = 3,14.
2. Иногда оперируют диаметром, а не радиусом круга. В этом случае к вычислениям добавляется одна операция: диаметр умножают сам на себя, затем на число π, а произведение делят на 4.
3. Если известна длина окружности С и ее радиус R и нужно выяснить площадь круга, ограниченного этой окружностью, не понадобится даже π. Используют следующую формулу: значение С делят пополам и умножают на R. Полученное чисто и будет искомой величиной.

Способов определения того, чему равна площадь круга, достаточно много. Чаще всего, если возникает подобная задача, на ум приходит знакомая еще со школьной скамьи формула «эс равно пи эр квадрат».

Источник

Как рассчитать площадь сечения трубы – простые и проверенные способы

Произвести расчет сечения трубы довольно просто, ведь для этого есть ряд стандартных формул, а также многочисленные калькуляторы и сервисы в интернете, которые могут выполнить ряд простых действий. В данном материале мы расскажем о том, как рассчитать площадь сечения трубы самостоятельно, ведь в некоторых случаях нужно учитывать ряд конструкционных особенностей трубопровода.

Формулы вычислений

При проведении вычислений нужно учитывать, что по существу трубы имеют форму цилиндра. Поэтому для нахождения площади их сечения можно воспользоваться геометрической формулой площади окружности. Зная внешний диаметр трубы и значение толщины его стенок, можно найти показатель внутреннего диаметра, который понадобится для вычислений.

Стандартная формула площади окружности такова:

π – постоянное число, равное 3,14;

R – величина радиуса;

S – площадь сечения трубы, вычисленная для внутреннего диаметра.

Порядок расчета

Поскольку главная задача – это найти площадь проходного сечения трубы, основная формула будет несколько видоизменена.

В результате вычисления производятся так:

D – значение внешнего сечения трубы;

N – толщина стенок.

Примите к сведению, что, чем больше знаков в числе π вы подставите в расчеты, тем точнее они будут.

Приведем числовой пример нахождения поперечного сечения трубы, с наружным диаметром в 1 метр (N). При этом стенки имеют толщину в 10 мм (D). Не вдаваясь в тонкости, примем число π равным 3,14.

Итак, расчеты выглядят следующим образом:

S=π×(D/2-N) 2 =3,14×(1/2-0,01) 2 =0,754 м 2 .

Физические характеристики труб

Стоит знать, что показатели площади поперечного сечения трубы напрямую влияют на скорость транспортировки газообразных и жидких веществ. Поэтому крайне важно заложить в проект трубы с правильным сечением. Кроме того, на выбор диаметра трубы будет влиять еще и рабочее давление в трубопроводе. Читайте также: «Как посчитать площадь трубы – способы и формулы расчета».

Также в процессе проектирования трубопроводов стоит учитывать химические свойства рабочей среды, а также ее температурные показатели. Даже если вы знакомы с формулами, как найти площадь сечения трубы, стоит изучить дополнительный теоретический материал. Так, информация относительно требований к диаметрам трубопроводов под горячее и холодное водоснабжение, отопительные коммуникации или транспортировку газов, содержатся в специальной справочной литературе. Значение имеет также сам материал, из которого произведены трубы.

Выводы

Таким образом, определение площади сечения трубы является очень важным, однако, в процессе проектировки нужно обращать внимание на характеристики и особенности системы, материалы трубных изделий и их прочностные показатели.

Источник

Стереометрия. Площадь сечения через площадь проекции сечения.

Что значит поперечное сечение

Перед тем как раскрыть основное понятие, нужно расшифровать значение термина и понять, чем провод отличается от кабеля. Провод является проводником, который используется, чтобы соединить несколько участков электрической цепи. Может иметь одну или много токовых проводящих жильных элементов. Они в свою очередь могут быть голыми, изолированными, одножильными и многожильными.

Площадь среза проводника

Первые используются в воздушных линиях электрических передач. Вторые применяются в электрических устройствах, щитках или шкафах. В быту они находятся внутри электрической проводки.

К сведению! Изолированные и одножильные проводники используются везде, а многожильные применяются там, где нужны изгибы с малым радиусом.

Что собой представляет поперечное сечение

Поперечным сечением называется фигура, которая образуется от проводникового рассечения плоскостью направления. Площадь, которая получена при перпендикулярном разрезе любого вида провода, указывается в квадратных миллиметрах. Это важный параметр для расчета электрической сети.

Определение основных понятий

Прежде чем погружаться в последовательность расчетов и узнать чему равна площадь окружности, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.

Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу.

Если говорить простым языком, окружность — это замкнутая линия, как, например, кольцо и шина. Круг — плоская фигура, ограниченная окружностью, как глобус и мяч.

Ещё мы рассказывали о том, как найти площадь треугольника, возможно, тебе будет интересно

Сфера применения

Поперечное сечение на чертеже изображено в виде фигуры, которая образована делением детали плоскостью. Используется в электротехнике, электричестве, когда рассматривается проводниковая жила под прямым углом к его продольной половине. Через поделенную жилу проходят электроны.

Обратите внимание! Диаметр жилы — это не сечение. Для определения площади жилы нужно использовать специальную формулу определения круга.

Зная, какая величина разреза провода, длина и удельное сопротивление, можно узнать, какое имеет сопротивление проводник электротоку, проходящий сквозь его структуру. Если неправильно подобрать разрез проводника, это может привести к возгоранию электрической проводки в системе в результате его перегрева, оплавления.

Вам это будет интересно Особенности измерения освещенности в люксах

Строительство — основная сфера применения проводов

Целью расчета площади поперечного сечения может быть получение нужного количества электроэнергии для нормальной работы электрических приборов, исключение переплат неиспользуемым энергоносителем, подключение мощной техники к сетевому напряжению, предотвращение возгорания участка, исключение оплавки слоя изоляции, предотвращение появления короткого замыкания в бытовой и промышленной сетях. Также это может быть получение правильной организации системы освещения.

К сведению! Нормальным сечением проводника для освещения является показатель 1,5 мм² для линии и 4-6 мм² для ввода.

Общая информация о кабеле и проводе

При работе с проводниками необходимо понимать их обозначение. Существуют провода и кабеля, которые отличаются друг от друга внутренним устройством и техническими характеристиками. Однако многие люди часто путают эти понятия.
Проводом является проводник, имеющий в своей конструкции одну проволоку или группу проволок, сплетенных между собой, и тонкий общий изоляционный слой. Кабелем же называется жила или группа жил, имеющих как собственную изоляцию, так и общий изоляционный слой (оболочку). Каждому из типов проводников будут соответствовать свои методы определения сечений, которые почти схожи.

Чем можно делать расчеты поперечного сечения

Иногда приходится измерять поперечное сечение самостоятельно, поскольку на провод не нанесена маркировка. Это не повод, чтобы не использовать его. Сперва нужно выяснить, из какого материала была сделана жила. Есть белая алюминиевая, медная красная и латунная желтая. После этого необходимо рассчитать площадь. Для этого следует выяснить проводниковый диаметр, убрав изоляцию. Диаметр можно измерить, используя:

• штангенциркуль, микрометр;
• карандаш и линейку.

Важно! Во втором случае результат будет приблизительным. Его использовать следует в крайних случаях. Лучше рассчитывать диаметр по формуле и штангенциркулем.

Штангенциркуль

Сделать штангенциркулем можно замер провода, который имеет любые размеры. Для этого нужно поместить его между штангенциркульными щипцами. Сделать так, чтобы они смотрены на деление шкалы. Затем подсчитать значение.

Штангенциркуль

Целые числа можно получить по верхней шкале, а десятичные — по нижней.

Карандаш + линейка

Если штангенциркуля нет, а длина оголенного проводника позволяет сделать его накрутку на карандаш длиной не меньше 1 см, можно использовать данный способ. Все, что нужно – подсчитать витки, которые поместились на отрезке длины 1 см. Диаметр получается делением длины отрезка на витки.

С помощью карандаша и линейки замеры будут не совсем точными

Обратите внимание! Точность измерения будет зависеть от того, как плотно была сделана намотка, и какая у нее длина.

Расчет площади

Площадь простейших геометрических фигур находят, сравнивая их с квадратом известной площади. Это удобно тем, что площадь квадрата легко вычислить. Некоторые формулы вычисления площади геометрических фигур, приведенные ниже, получены именно таким путем. Также для вычисления площади, особенно многоугольника, фигуру делят на треугольники, вычисляют площадь каждого треугольника по формуле, а потом складывают. Площадь более сложных фигур вычисляют с помощью математического анализа.

Формулы для вычисления площади

• Квадрат:
  сторона в квадрате.
• Прямоугольник:
  произведение сторон.
• Треугольник (известна сторона и высота):
  произведение стороны и высоты (расстояния от этой стороны до ребра), деленное пополам. Формула:
  A = ½ah
  , где
  A
  — площадь,
  a
  — сторона, и
  h
  — высота.
• Треугольник (известны две стороны и угол между ними):
  произведение сторон и синуса угла между ними, деленное пополам. Формула:
  A = ½ab
  sin(α), где
  A
  — площадь,
  a
  и
  b
  — стороны, и α — угол между ними.
• Равносторонний треугольник:
  сторона, в квадрате, деленная на 4 и умноженная на квадратный корень из трех.
• Параллелограмм:
  произведение стороны и высоты, измеряемой от этой стороны, до противоположной.
• Трапеция:
  сумма двух параллельных сторон, умноженная на высоту, и деленная на два. Высота измеряется между этими двумя сторонами.
• Круг:
  произведение квадрата радиуса и π.
• Эллипс:
  произведение полуосей и π.

Читать также: Как запрессовать сайлентблок без наружной обоймы

Вычисление площади поверхности

Найти площадь поверхности простых объемных фигур, таких как призмы, можно по развертке этой фигуры на плоскости. Развертку шара получить таким образом невозможно. Площадь поверхности шара находят с помощью формулы, умножая квадрат радиуса на 4π. Из этой формулы следует, что площадь круга в четыре раза меньше площади поверхности шара с таким же радиусом.

Площади поверхности некоторых астрономических объектов: Солнце — 6,088 x 10¹² квадратных километров; Земля — 5,1 x 10⁸; таким образом, площадь поверхности Земли примерно в 12 раз меньше площади поверхности Солнца. Площадь поверхности Луны приблизительно равна 3,793 x 10⁷ квадратных километров, что примерно в 13 раз меньше площади поверхности Земли.

Планиметр

Площадь также можно вычислить с помощью специального прибора — планиметра. Существуют несколько видов этого прибора, например полярный и линейный. Также, планиметры бывают аналоговыми и цифровыми. В дополнение к другим функциям, в цифровые планиметры можно вводить масштаб, что облегчает измерение объектов на карте. Планиметр измеряет расстояние, пройденное по периметру измеряемого объекта, а также направление. Расстояние, пройденное планиметром параллельно его оси, не измеряется. Эти устройства используются в медицине, биологии, технике, и сельском хозяйстве.

В чем измеряется поперечное сечение

После определения диаметра указанными способами площадь сечения можно определить по формуле или специальной таблице. Измеряется она в квадратных миллиметрах. Данная единица измерения производная согласно единой международной системе измерений.

Вам это будет интересно Особенности ШДУП У4

Мера измерения

При этом разрез жил всегда круглый.

Самостоятельный гидравлический расчет трубопровода

Гидравлический расчёт при разработке проекта трубопровода направлен на определение диаметра трубы и падения напора потока носителя.

Данный вид расчёта проводится с учетом характеристик конструкционного материала, используемого при изготовлении магистрали, вида и количества элементов, составляющих систему трубопроводов(прямые участки, соединения, переходы, отводы и т. д.), производительности,физических и химических свойств рабочей среды.

Многолетний практический опыт эксплуатации систем трубопроводов показал, что трубы, имеющие круглое сечение, обладают определенными преимуществами перед трубопроводами, имеющими поперечное сечение любой другой геометрической формы:

• минимальное соотношением периметра к площади сечения, т.е. при равной способности, обеспечивать расход носителя, затраты на изолирующие и защитные материалы при изготовлении труб с сечением в виде круга, будут минимальными;
• круглое поперечное сечение наиболее выгодно для перемещения жидкой или газовой среды сточки зрения гидродинамики, достигается минимальное трение носителя о стенки трубы;
• форма сечения в виде круга максимально устойчива к воздействию внешних и внутренних напряжений;
• процесс изготовления труб круглой формы относительно простой и доступный.

Подбор труб по диаметру и материалу проводится на основании заданных конструктивных требований к конкретному технологическому процессу. В настоящее время элементы трубопровода стандартизированы и унифицированы по диаметру. Определяющим параметром при выборе диаметра трубы является допустимое рабочее давление, при котором будет эксплуатироваться данный трубопровод.

Основными параметрами, характеризующими трубопровод являются:

• условный (номинальный) диаметр – DN;
• давление номинальное – PN;
• рабочее допустимое (избыточное) давление;
• материал трубопровода, линейное расширение, тепловое линейное расширение;
• физико-химические свойства рабочей среды;
• комплектация трубопроводной системы (отводы, соединения, элементы компенсации расширения и т.д.);
• изоляционные материалы трубопровода.

Условный диаметр (проход) трубопровода (DN) – это условная безразмерная величина, характеризующая проходную способность трубы, приблизительно равная ее внутреннему диаметру. Данный параметр учитывается при осуществлении подгонки сопутствующих изделий трубопровода (трубы, отводы, фитинги и др.).

Условный диаметр может иметь значения от 3 до 4000 и обозначается: DN 80.

Условный проход по числовому определению примерно соответствует реальному диаметру определенных отрезков трубопровода.

Численно он выбран таким образом, что пропускная способность трубы повышается на 60-100% при переходе от предыдущего условного прохода к последующему.

Давление номинальное (PN) – это безразмерная величина, характеризующая максимальное давление рабочего носителя в трубе заданного диаметра, при котором осуществима длительная эксплуатация трубопровода при температуре 20°C.

Значения номинального давления были установлены на основании продолжительной практики и опыта эксплуатации: от 1 до 6300.

Номинальное давление для трубопровода с заданными характеристиками определяется по ближайшему к реально создаваемому в нем давлению. При этом,вся трубопроводная арматура для данной магистрали должна соответствовать тому же давлению. Расчет толщины стенок трубы проводится с учетом значения номинального давления.

Основные положения гидравлического расчета

Рабочий носитель (жидкость, газ, пар), переносимый проектируемым трубопроводом, в силу своих особых физико-химических свойств определяет характер течения среды в данном трубопроводе. Одним из основных показателей характеризующих рабочий носитель, является динамическая вязкость, характеризуемая коэффициентом динамической вязкости – μ.

Инженер-физик Осборн Рейнольдс (Ирландия), занимавшийся изучением течения различных сред, в 1880 году провел серию испытаний, по результату которых было выведено понятие критерия Рейнолдса (Re) – безразмерной величины, описывающей характер потока жидкости в трубе. Расчет данного критерия проводится по формуле:

Критерий Рейнольдса (Re) дает понятие о соотношении сил инерции к силам вязкого трения в потоке жидкости. Значение критерия характеризует изменение соотношения указанных сил, что, в свою очередь, влияет на характер потока носителя в трубопроводе. Принято выделять следующие режимы потока жидкого носителя в трубе в зависимости от значения данного критерия:

ламинарный поток (Re

Формула измерения площади поперечного сечения

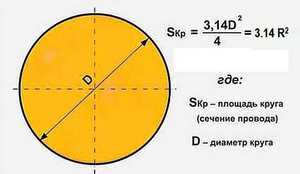
Рассчитать поперечное сечение, а именно площадь можно через формулу круга S = π * R2, где первым звеном является площадь круга, вторым — константа Пи 3,14, а третьим — радиус. Принимая во внимание тот факт, что радиус является одной второй диаметра, то формула может быть преобразована по желанию. Рассчитывая площадь, следует использовать диаметр.

Обратите внимание! Чтобы определить сечение многожильного провода, нужно вычислить площадь одной жилы, а затем полученное значение перемножить на количество проводниковых жил.

Определяя диаметр проводника комнатной электропроводки, нужно взять во внимание показатель одновременной максимальной потребительской нагрузки. Принимая в расчет показатель мощности, берется сечение линий, идущих от центра счетчика и вводных автоматов к распределительной коробке. Это места с суммарной нагрузкой всех подсоединенных потребителей. Делать выбор лучше в пользу медного провода с жилами не меньше 6 мм².

Формула для расчета

Поперечным сечением называется площадь среза под углом 90° к оси. Рассчитывать его на проводнике можно штангенциркулем, карандашом, линейкой. Измеряется оно в квадратных миллиметрах. Подсчитывается по специальной формуле, представленной выше. Ничего сложного в этом нет, главное — выбрать самый точный вариант.

Материалы проводников

Количество энергии, какую передает проводник, зависит от ряда факторов, главный из которых – это материал токопроводящих жил. Материалом жилок проводов и кабелей могут выступать следующие цветные металлы:

1. Алюминий. Дешевые и легкие проводники, что является их преимуществом. Им присуще такие отрицательные качества, как низкая электропроводность, склонность к механическим повреждением, высокое переходное электросопротивление окисленных поверхностей;
2. Медь. Наиболее популярные проводники, имеющие, по сравнению с другими вариантами, высокую стоимость. Однако им присуще малое электрическое и переходное на контактах сопротивление, достаточно высокая эластичность и прочность, легкость в спайке и сварке;
3. Алюмомедь. Кабельные изделия с жилами из алюминия, которые покрыты медью. Им свойственна чуть меньшая электропроводность, чем у медных аналогов. Также им присуще легкость, среднее сопротивление при относительной дешевизне.

Некоторые способы определения сечения кабелей и проводов будут зависеть именно от материала их жильной составляющей, который напрямую влияет на пропускную мощность и силу тока (метод определения сечения жил по мощности и току).

Способы определения сечения провода пошагово

Существует несколько способов для измерения сечения по диаметру жилы. Если провод одножильный, то замеры будут производиться сразу на нем, а вот из бухты кабеля необходимо выпутать один проводник. После этого его очищают от изоляции, чтобы остался только металл.

Чтобы вычислить площадь круга через величину радиуса, применяется расчет по формуле: S = π × R2­, где:

• π – константа равная 3,14;
• R – радиус окружности.

Но, в связи с тем, что с практической точки зрения гораздо проще вычислить диаметр, равный двум радиусам, формула расчета примет такой вид: S = π × (D/2)2. В зависимости от способов замеров диаметра выделяют такие методы вычисления сечения.

По диаметру с помощью штангенциркуля или микрометра

Наиболее актуальным вариантом, чтобы измерить диаметр являются такие приборы, как штангенциркуль и микрометр. Данные устройства позволяют измерить диаметр максимально точно. Для этого вам понадобится провод и микрометр.

Для этого фиксатор Б переводится в открытое положение. Ручка микрометра откручивается на такое расстояние, чтобы провод легко поместился в пространстве между щупами А. Затем при помощи ручки Г прибор закручивается до срабатывания трещотки. После этого фиксируются показания по всем трем шкалам в точке В.

В данном примере диаметр составляет 1,4 мм, следовательно, чтобы вычислить сечение, необходимо S = 3,14 × 1,4 × 1,4 / 4 = 1,53 мм². Такую же процедуру определения сечения можно произвести, используя штангенциркуль. Преимуществом такого метода является возможность измерить любой проводник круглого сечения, даже если он уже установлен и эксплуатируется для питания какого-либо электрического прибора. Основной недостаток метода – это высокая стоимость приспособлений, естественно, что приобретать их для пары замеров совершенно нецелесообразно.

По диаметру с помощью карандаша или ручки

Данный способ определения сечения основан на том факте, что по всей длине у провода одинаковый диаметр. Возьмите обычный карандаш, ручку или фломастер, на который намотайте провод по спирали. Чтобы исключить толщину изоляции, ее необходимо срезать по всей длине. Кольца должны располагаться максимально плотно, чем больше пространство между кольцами, тем ниже точность.

Так как все провода имеют одинаковую толщину, то для определения диаметра медных проводов, измерьте длину всей намотки и разделите на количество витков. В данном примере D = 15 мм / 15 витков = 1 мм, соответственно, используя ту же формулу расчета, получим сечение S = 3,14 × 1 × 1 / 4 = 0,78 мм². Заметьте, чем больше витков вы сделаете, тем более точно определите сечение.

Стоит отметить, что преимущество такого метода в том, что для определения сечения можно использовать только подручные средства. Недостаток – низкая точность и возможность намотки только тонких проводников. В примере использовался относительно тонкий провод, но расстояние между витками уже просматривается. Из-за чего точность оставляет желать лучшего, разумеется, что алюминиевую проволоку таким способом согнуть не удастся.

По диаметру с помощью линейки

Сразу оговоримся, что для измерения линейкой можно брать только относительно толстый провод, чем меньше толщина, тем ниже точность. Диаметр жилки при этом может определяться ниткой или бумагой, второй вариант является наиболее предпочтительным, так как дает большую точность.

Оторвите небольшую полоску и загните ее с одной стороны. Предпочтительнее более тонкая бумага, поэтому не нужно складывать листок в несколько раз. Затем бумагу прикладывают к проводу и заворачивают по окружности до соприкосновения полоски. В месте соприкосновения ее загибают второй раз и прикладывают к линейке для измерения.

Через полученную длину окружности L находят диаметр жилки D = L / 2 π, а расчет сечения выполняется как показывалось ранее. Данный метод определения сечения хорошо подходит для крупных алюминиевых жил. Но точность в этом методе наиболее низкая.

По диаметру с помощью готовых таблиц

Этот метод подходит для проводов стандартного сечения. К примеру, вы уже определили диаметр по одному из вышеприведенных методов. После чего вы используете таблицу для определения сечения.

Зависимость тока, мощности и сечения жил

Измерить и произвести расчеты площади сечения кабеля по диаметру жилы недостаточно. Перед прокладкой проводки или иных типов электросетей необходимо также знать пропускную способность кабельной продукции.

Выбирая кабель, необходимо руководствоваться несколькими критериями:
• сила электротока, которую будет пропускать кабель;
• мощность потребителей;
• токовая нагрузка, оказываемая на кабель.

Мощность

Самым важным параметром при электромонтажных работах (в частности прокладке кабелей) является пропускная мощность. От сечения проводника зависит максимальная мощность передаваемой по нему электроэнергии. Поэтому крайне важно знать общую мощность источников потребления энергии, которые будут подключены к проводу. Обычно производители бытовой техники, приборов и иных электротехнических изделий указывают на этикетке и в прилагаемой к ним документации максимальную и среднюю мощность потребления.

Например, машина для стирки белья может потреблять электроэнергию в диапазоне от десятков Вт/ч при режиме полоскания до 2,7 кВт/ч при нагреве воды.

Соответственно, к ней должен подключаться провод с тем сечением, которого хватит для передачи электроэнергии максимальной мощности. Если к кабелю подключается два и более потребителя, то общая мощность определяется путем сложения предельных значений каждого из них. Усредненная мощность всех электроприборов и осветительных устройств в квартире редко превышает 7500 Вт для однофазной сети. Соответственно, сечения кабелей в электропроводке необходимо подбирать под это значение.

Рекомендуется округлять сечение в сторону увеличения мощности из-за возможного увеличения потребляемой электроэнергии в будущем. Обычно берут следующую по числу площадь сечения от рассчитанной величины. Так, для значения общей мощности 7,5 кВт необходимо использовать медный кабель с сечением жилы 4 мм2, который способен пропустить около 8,3 кВт. Сечение проводника с алюминиевой жилой в таком случае должно быть не менее 6 мм2, пропускающее мощность тока от 7,9 кВт.

Площадь круга описанного вокруг квадрата

Очень легко можно найти площадь круга описанного вокруг квадрата.
Для этого потребуется только сторона квадрата и знание простых формул. Диагональ квадрата будет равна диагонали описанной окружности. Зная сторону a ее можно найти по теореме Пифагора: отсюда . После того, как найдем диагональ – мы сможем рассчитать радиус: . И после подставим все в основную формулу площади круга описанного вокруг квадрата:

Рассмотрим пример расчета площади круга, описанного вокруг квадрата. Задача: дан квадрат, вписанный в круг. Его сторона a = 4 см. Найдите площадь окружности. Для начала рассчитаем длину диагонали d. Теперь подставляем данные в формулу

Зная несколько простых правил и теорему Пифагора, мы смогли рассчитать площадь описанной вокруг квадрата окружности.

Источник