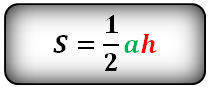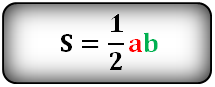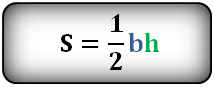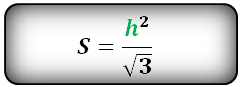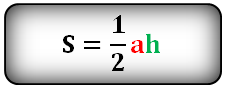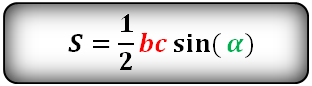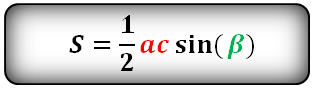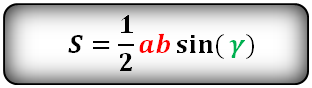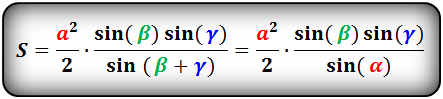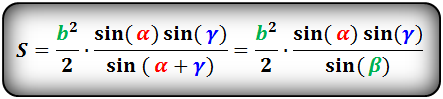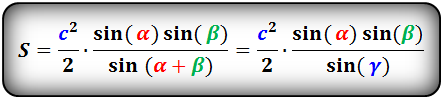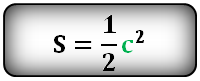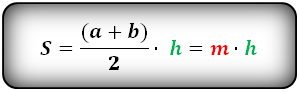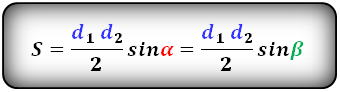Способы вычисления площадей формулы

Площади геометрических фигур: список формул, описание, примеры

Содержание:

Для решения практических задач иногда приходится вычислять площади геометрических фигур. Они, например, нужны при измерениях земельных участков, поверхностей при проведении ремонтных и строительных работ. Рассмотрим, что такое площадь геометрической фигуры, по каким формулам она определяется в разных ситуациях.

Площади всех фигур в геометрии

Площадью называют численную характеристику поверхности, которая показывает сколько квадратов с размером 1 × 1 занимает объект на плоскости. Изменяется в квадратных единицах – метрах, сантиметрах, километрах и т. д.

Для нарисованного по клеточкам четырёхугольника с прямыми углами это делается простым подсчётом с перемножением полученных значений. Для квадрата на примере это 100 см2: 10 × 10 см.

В математике насчитывается менее десятка фигур – замкнутых множеств, сформированных точками, площадь которых можно вычислить. Общий принцип расчётов сформирован благодаря интегральному счислению.

Формулы площадей фигур по геометрии

Если известен диаметр – четверти его квадрата на π.

S = \pi \frac <4>, потому что d = \frac <1><2>r, d^2 = \frac <1><4>r^2 .

Кольцо круга: разница между площадями кольца и круга.

Четырёхугольники

Квадрат: размеры сторон перемножаются.

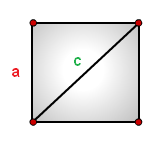
Также площадь вычисляется как половина квадрата диагонали.

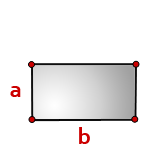
Прямоугольник: произведение соседних сторон – длины на ширину.

Параллелограмм: умножение длины стороны на опущенную к ней высоту.

Вторая формула применяется, когда известны длины сторон с углом между ними – произведение сторон на sin угла, под которым они пересекаются.

Ромб – параллелограмм с равными сторонами. Если известна сторона, площадь ромба вычисляется как произведение sin угла между сторонами на их длину в квадрате.

Если в задании даны длины диагоналей, площадь определяется как половина их произведения.

При наличии одной диагонали (полудиагонали) и стороны, неизвестные данные вычисляются по теореме Пифагора.

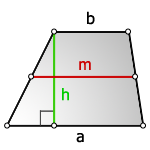
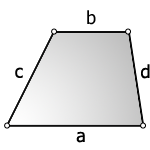
Трапеция: полусумма длин верхнего и нижнего оснований на высоту геометрической фигуры.

Когда даны средняя линия и высота, площадь находят путём перемножения их значений.

Выпуклый четырёхугольник: половина длины диагоналей, перемноженная на sin угла, который они образуют.

Вписанный в окружность 4-угольник: площадь вычисляется как корень квадратный из произведения разности периметра на длину каждой стороны.

В случае с прямоугольником, квадратом формула упрощается.

Треугольники

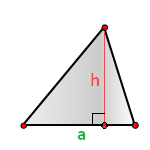
Половины стороны на проведённую к ней высоту.

Пары любых сторон на sin образуемого ими угла:

Квадрата полупериметра геометрической фигуры на тангенсы половин углов.

S = p 2 * tgα/2 * tgβ/2 * tgγ/2.

Корню квадратному произведения разницы полупериметров и сторон.

Квадрата длины стороны на синусы смежных углов, разделённому на удвоенный синус третьего, противоположного ей угла.

При известной высоте: отношению её произведения на синус угла, откуда та опущена, к двойному произведению синусов остальных углов.

Для прямоугольного 3-угольника, по сути, половины прямоугольника, применимо выражение:

Источник

Формулы площади геометрических фигур.

Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.

Формулы площади треугольника

Формула Герона

где S — площадь треугольника,
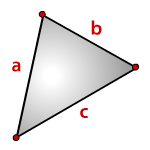
a, b, c — длины сторон треугольника,
h — высота треугольника,
γ — угол между сторонами a и b ,
r — радиус вписанной окружности,
R — радиус описанной окружности,

p =	a + b + c	— полупериметр треугольника.
	2

Формулы площади квадрата

Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.

Формула площади прямоугольника

Формулы площади параллелограмма

Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.

Формулы площади ромба

Формулы площади трапеции

Формула Герона для трапеции

S =	a + b	√ ( p-a )( p-b )( p-a-c )( p-a-d )
	| a — b |

где S — площадь трапеции,
a, b — длины основ трапеции,
c, d — длины боковых сторон трапеции,

p =	a + b + c + d	— полупериметр трапеции.
	2

Формулы площади выпуклого четырехугольника

Формула площади четырехугольника по длине диагоналей и углу между ними Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:

где S — площадь четырехугольника,
d ₁, d ₂ — длины диагоналей четырехугольника,
α — угол между диагоналями четырехугольника.

Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности)
Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности

Формула площади четырехугольника по длине сторон и значению противоположных углов

a , b , c , d — длины сторон четырехугольника,

p = a + b + c + d 2 — полупериметр четырехугольника,

θ = α + β 2 — полусумма двух противоположных углов четырехугольника.

Формула площади четырехугольника, вокруг которого можно описать окружность

Формулы площади круга

Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на число пи.

Источник

Формулы площадей всех основных фигур

1. Формула площади круга через радиус или диаметр

Зная диаметр или радиус круга, можно найти его площадь.

r — радиус круга

D — диаметр

Формула площади круга, (S):

2. Формула расчета площади треугольника

h — высота треугольника

a — основание

Площадь треугольника (S):

3. Площадь треугольника, формула Герона

a , b , c , — стороны треугольника

p— полупериметр, p=( a + b + c )/2

Формула ( Герона ) площади треугольника через полупериметр ( S ):

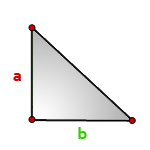
4. Площадь прямоугольного треугольника по катетам

Зная катеты прямоугольного треугольника, можно по формуле, найти его площадь.

a , b — катеты треугольника

Формула площади прямоугольного треугольника, (S):

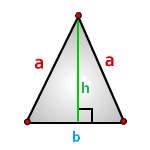
5. Как вычислить площадь равнобедренного треугольника ?

b — основание треугольника

a — равные стороны

h — высота

Формула площади треугольника через высоту h и основание b , ( S ):

Формула площади треугольника через, стороны a , b , (S):

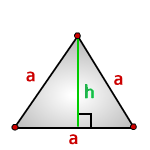
6. Площадь равностороннего треугольника равна:

Формулы расчета, площади равностороннего треугольника.

a — сторона треугольника

h — высота

Площадь треугольника только через сторону a , (S):

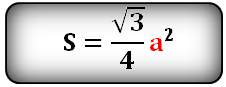
Площадь треугольника только через высоту h , ( S ):

Площадь треугольника через сторону a и высоту h , (S):

7. Найти площадь треугольника, угол и две стороны

Зная у треугольника, две стороны и синус угла между ними, находим по формуле, его площадь.

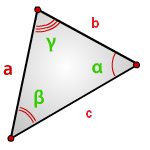
a , b , c — стороны треугольника

α , β , γ — углы

Формулы площади треугольника, через две стороны и угол между ними, ( S ):

8. Площадь треугольника по стороне и двум углам, формула.

a , b , c — стороны треугольника

α , β , γ — противолежащие углы

Площадь треугольника через сторону и два угла (S):

9. Формула расчета площади прямоугольника

b — длина прямоугольника

a — ширина

Формула площади прямоугольника, (S):

10. Как рассчитать площадь квадрата через диагональ или сторону

a — сторона квадрата

c — диагональ

Формула площади квадрата через сторону a , (S):

Формула площади квадрата через диагональ c , (S):

11. Формулы площади параллелограмма

1. Формула площади параллелограмма через стороны и углы

a, b — стороны параллелограмма

α , β — углы параллелограмма

Формула площади через стороны и углы параллелограмма, ( S ):

2. Формула площади параллелограмма через сторону и высоту

a, b — стороны параллелограмма

H _b — высота на сторону b

H _a — высота на сторону a

Формула площади через стороны и высоты параллелограмма, (S):

3. Формула площади параллелограмма через диагонали и угол между ними

D — большая диагональ

d — меньшая диагональ

α , β — углы между диагоналями

Формула площади через диагонали параллелограмма и угол между ними , (S):

12. Площадь произвольной трапеции

1. Формула площади трапеции через основания и высоту

b — верхнее основание

a — нижнее основание

m — средняя линия

h — высота трапеции

Формула площади трапеции, (S):

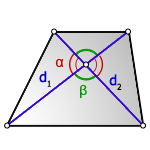
2. Формула площади трапеции через диагонали и угол между ними

d ₁, d ₂ — диагонали трапеции

α , β — углы между диагоналями

Формула площади трапеции, (S):

3. Формула площади трапеции через четыре стороны

b — верхнее основание

a — нижнее основание

c, d — боковые стороны

Формула площади трапеции, (S):

13. Площадь равнобедренной трапеции

1. Формула площади равнобедренной трапеции через стороны и угол

b — верхнее основание

a — нижнее основание

c — равные боковые стороны

α — угол при нижнем основании

Формула площади равнобедренной трапеции через стороны, (S):

Формула площади равнобедренной трапеции через стороны и угол, (S):

2. Формула площади равнобокой трапеции через радиус вписанной окружности

R — радиус вписанной окружности

D — диаметр вписанной окружности

O — центр вписанной окружности

H — высота трапеции

α , β — углы трапеции

Формула площади равнобокой трапеции через радиус вписанной окружности, (S):

СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:

3. Формула площади равнобедренной трапеции через диагонали и угол между ними

d — диагональ трапеции

α , β — углы между диагоналями

Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):

4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

m — средняя линия трапеции

c — боковая сторона

α , β — углы при основании

Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):

5. Формула площади равнобедренной трапеции через основания и высоту

b — верхнее основание

a — нижнее основание

h — высота трапеции

Формула площади равнобедренной трапеции через основания и высоту, (S):

Источник