Способы вычисления двузначных чисел

Как научить ребёнка считать в уме двузначные числа во 2 классе

Взрослому человеку не стоит объяснять насколько важно уметь считать в уме. Конечно, в повседневной жизни нам не надо за считанные секунды перемножать друг на друга семизначных «монстров». Обычно большинству людей хватает умения быстро складывать и перемножать числа значительно меньших значений. Но чтобы оперировать в уме даже ими, важно ещё в школьном возрасте развить в детях этот навык. А как научить ребёнка считать в уме двузначные числа второкласснику, если в школе этому не уделяется большого внимания? Достаточно просто. Конечно, придётся потратить на это некоторое количество времени, сил и нервов, но зато это позволит избежать многих проблем в будущем. Причём и маленькому человеку, и его родителям.

Сразу стоит оговориться, что в дальнейшем речь пойдёт об умении складывать и вычитать в уме двузначные числа, т.к. умножение, согласно современным школьным программам, детки начинают проходить только в конце второго класса.

И ещё: формулы в примерах приведены исключительно для понимания взрослыми сути методики. Второклассникам их показывать стоит только в том случае, если они неплохо справляются с решением подобных задачек в своих тетрадях. В противном случае они могут просто запутаться в числах. А в случае крайней необходимости для наглядности можно воспользоваться, к примеру, счётными палочками.

С чего начать обучение счету в уме для второклассника

Сразу стоит сказать, что приступать к выработке умения считать в уме двухзначные числа ребёнку-второкласснику можно только в том случае, если он без труда работает в уме с цифрами от 0 до 9. Если же младший школьник до сих пор использует для подсчётов в пределах 10-18 собственные пальцы, то для начала его следует научить работать с подобными примерами без использования подручных средств.

В том случае, если с однозначными числами ребёнок общается уже на «ты», можно приступать к дальнейшей работе. На этом этапе школьника стоит научить быстро решать примеры с цифрами 7, 8 и 9. Этот навык поможет маленькому математику отработать навык работы с составом числа.

Тут все просто: цифра 7, 8 или 9 раскладывается таким образом, чтобы после прибавки одного кусочка к двузначному числу получилось число круглое, а затем в разряд единиц добавить остаток:

Аналогичная ситуация и с вычитанием:

Иногда педагоги рекомендуют применять методику чуть сложнее. Прибавлять сначала десяток, а потом вычитать из него количество единиц, которых вычитаемому не хватает до 10: 45+7=45+(10-3)=55-3=52. Однако этот способ ребёнку воспринимать сложнее. Лучше его объяснить позднее, когда навык счёта в уме с вышеуказанными тремя цифрами уже будет наработан. Вот тогда для упрощения некоторых вычислений пригодится и данная методика.

После того, как ребёнок освоит решение примеров с двузначными числами и цифрами 7, 8, 9 можно приступать непосредственно к обучению счёта в уме двузначных чисел.

Работа с двузначными числами

На самом деле работа в уме с двузначными (и даже трёхзначными) числами достаточно проста. Здесь применяются те же алгоритмы, что и при решении примеров с цифрами 7, 8, 9. Различия лишь в том, что работать приходится сразу и с единицами, и с десятками.

Сложение двузначных чисел в уме

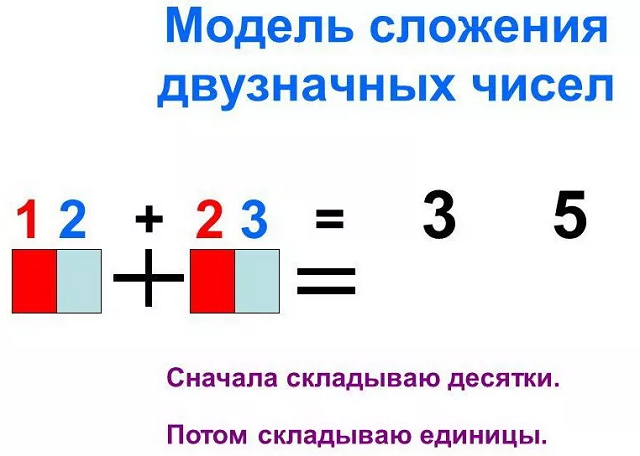
Ребёнку надо объяснить, что если последние цифры обоих чисел меньше 5 или их сумма меньше или равна 9, то подсчёт сводится к элементарному суммированию единиц и десятков:
21+16=(20+1)+(10+6)=(20+10)+(1+6)=30+7=37.

Если же последние цифры больше 5 или их сумма больше 9, то можно применить одну из двух методик счёта, в основе которых лежит опять же разложение числа по составу.
В первом случае следует поступить так же, как и в вариантах с цифрами 7, 8, 9. Округлить первое слагаемое за счёт «разбора на кусочки» единиц второго слагаемого, а затем суммировать полученные числа:

Во втором – округлить второе слагаемое до круглого числа, произвести суммирование и вычесть лишний кусочек:

Вычитание двузначных чисел в уме

Второклассники, которые освоили сложение двухзначных чисел в уме, без труда осваивают и обратное действие – вычитание, поскольку применяются тут аналогичные алгоритмы.
В простых случаях десятки вычитаются из десятков, а единицы из единиц:

В более сложных случаях лучше применять метод округления:

А в чём же методика

Всё вышеописанное выглядит достаточно простым. Это и в самом деле так. Но просто это выглядит для родителей, которые учились значительно больше, чем два класса. Так что суть методик не столько в том, какие действия нужно делать в уме, сколько в поэтапном грамотном объяснении и отработке навыков путём постоянных тренировок.

Работать с ребёнком нужно регулярно. Объяснив один из алгоритмов в течение некоторого времени нужно закреплять навык, доводя его до автоматизма. Сильно мучить второклассника при этом не следует. Достаточно заниматься 10-15 минут в день, а если ребёнок хорошо справляется с заданиями, то хватит и 3-4 примеров. Но даже в последнем случае останавливаться на достигнутом не стоит. Если прекратить тренироваться, то алгоритмы могут забыться, а навык пропасть.

Занятия можно проводить по дороге в школу или из неё. Благо каких-то инструментов для этого не нужно. А можно делать это и дома, в форме игры, например: «В магазин». Можно играть и в развивающие счётные способности настольные игры типа математического лото.

Неплохим подспорьем в современном мире, где правят удалённые технологии, может стать и множество специально разработанных приложений для обучения быстрому счёту в уме, а также онлайн игры и сервисы. Кстати, в этом случае тоже нужно следить, чтобы младший школьник не слишком долго сидел, уткнувшись в телефон или монитор компьютера. Пятнадцати минут в день – вполне достаточно.

Поведение родителей

Чтобы ребёнок быстро освоил счёт двухзначных чисел в уме, родители должны создать доброжелательную атмосферу. Даже второклассник всё равно является ещё малышом и с большим удовольствием займётся интересным и весёлым делом, а не скучным образовательным процессом. Именно способствующую обучению атмосферу и должны обеспечить родители.

Кроме того, маме и папе надо запастись терпением, не ругаться, если у чада что-то не получается и, тем более, не заставлять его работать через силу. Пользы от этого точно не будет.

Источник

Как объяснить ребенку сложение и вычитание двухзначных чисел

Обучать ребенка арифметике довольно непросто, ведь она состоит из трёх этапов. Для начала придется разобраться с числами от 0 до 9, а потом со всем остальным. Однако и с двузначными числами нужно работать поэтапно. Пусть ребенок отработает действия с числами от 10 до 20, затем от 20 до 30 и так далее. Если вы примените правильные методы и организуете обучение в игровой форме, ребенок быстрее усвоит сложную арифметику.

Итак, обучение проходит в несколько этапов.

Подготовка

На этом этапе ребенок учится складывать и вычитать двузначные числа. Пусть ребенок сначала поработает с круглыми числами (научится их складывать и вычитать). После научите его выделять в числах разрядные слагаемые (34=30+4). Попробуйте объяснить ему, что в числе 34 получится 3 десятка и 4 единицы. Справиться с этим вам помогут счетные палочки. Это довольно практичный метод, который применяется в школах уже давно.

Примите к сведению, что счетные палочки можно легко заменить на детали лего или какой-нибудь конструктор: мелкие детали— это единицы, детали покрупнее— это десятки. Сразу после этого можно переходить к сложению и вычитанию круглых чисел.

Сложение и вычитание круглых чисел

Существуют разные способы обучения ребенка сложению и вычитанию круглых чисел.

• Во-первых, когда ребёнок понимает, что 20 равняется двум десяткам, а 30– это три десятка, он быстро научится считать. 20+30 — это тоже самое, что два десятка и три десятка получается пять десятков.
• Во-вторых, можно тренироваться на том же конструкторе. Возьмите 2 детали среднего размера, добавьте к ним ещё 3 детали среднего размера— и получается 5 деталей среднего размера. Получается 20+30=50.

По такому же принципу разберите и вычитание круглых чисел. Как только малыш усвоит эти несложные манипуляции, можно двигаться дальше.

Складываем и вычитаем числа без перехода через разряд

Чтобы разобраться с этим этапом, придётся объяснять действия на практике. Скажем, нужно выполнить следующее действие: 24+31. Тут уж нам придется изучить ещё 1 способ сложения/вычитания. Выкладываем палочки по горизонтальной линии — это будут наши десятки; а вертикально выложенные палочки— это единицы. Теперь складываете вертикальные палочки с вертикальными, а горизонтальные с горизонтальными. Так выкладываем 2 палочки горизонтально и 4 вертикально, а рядом— 3 горизонтальные и 1 вертикальную палочку. Сложив их, получаем 5 горизонтальных палочек и 5 вертикальных, то есть, окончательный ответ 55. Постепенно ребёнок усвоит, что единицы нужно добавлять к единицам, а к десяткам добавляются десятки.

Следующее, что вы можете разобрать с малышом— это научиться складывать и вычитать в столбик. Здесь необходимо объяснить будущему школьнику, что единицы записываются под единицами, а десятки под десятками. Возможно, будет полезно вначале разложить кусочки лего и найти результат, а потом провести расчет в столбик.

Таким же образом можно разобрать и вычитание ( с помощью палочек, кусочков Лего и записи в столбик). Если ребенок освоил технику со сложением, ему будет не трудно справиться и с вычитанием.

Сложение и вычитание чисел с переходом через разряд

Сложность выполнения сложения и вычитания чисел через разряд заключается в том, что тут придётся «занимать» и «запоминать» числа.

Попробуем решить такой пример (26+35) с помощью палочек.

1. Выкладываем числа палочками и складываем их по разрядам. У нас выходит 5 горизонтальных и 11 вертикальных палочек.
2. Теперь напомните малышу, что, выполняя арифметические действия 10 единиц равняются 1 десятку. Получается, 10 вертикальных палочек можно заменить 1 горизонтальной палочкой.
3. Выходит 6 десятков и 1 единица.
4. Отсюда видно, что при сложении единиц, у нас есть число больше 10. Эти 10 единиц мы заменяем 1 десятком. Теперь показываем ребёнку, что выполняя сложение и вычитание, начинать нужно с единиц. И если их получается 10 и больше, выделяем здесь десяток и прибавляем его к другим десяткам.

Как только этот этап пройден, можно рассмотреть и другие варианты сложения двузначных чисел.

• сначала к числу добавляем десятки, а потом единицы. (26+30+5=61)
• первое слагаемое делаем круглым, затем добавляем к нему второе слагаемое и вычитаем то число, которое добавили изначально. (26+4=30; 30+35=65; 65-4=61)
• плюсуем единицы с единицами, а десятки с десятками. Помните, если единиц больше 10, то добавляем 1 десяток. (20+30=50; 6+5=11; 50+10=60) Итого получается 61.

Вычитание тоже покажите на наглядном примере. Допустим, 53-27.

1. Делаем первое число (5 десятков и 3 единицы) и второе (2 десятка и 7 единиц)
2. Мы видим, что из 3 единиц невозможно вычесть 7 единиц. Значит, занимаем 1 десяток = 10 единиц.
3. Теперь из 13 единиц мы можем вычесть 7 единиц. А теперь отнимаем десятки. Тут важно напомнить ребёнку, что десятков у нас стало на 1 меньше. Значит, от 4 мы отнимаем 2.
4. Итого у нас получается 13-7=6 и 4-2=2. Значит, получается 53-27=26.

Завершив наглядный метод, начните считать и другими способами:

• сначала вычитаем в столбик: напомните ребёнку, что единицы вычитаться и складываются с единицами, а десятки с десятками. 53-27=26
• а теперь вычитаем десятки, а после единицы.

Чтобы объяснить ребёнку тонкости арифметических действий, возьмите в помощь счёты. Это удобно и практично. А ещё ребёнок мог бы записать числа на них и практиковаться, пока не дойдёт до автоматизма.

Помните, что каждый ребёнок индивидуален и выбирать способ обучения необходимо исходя из особенностей ребенка. Кому-то легко дается счет на палочках, кто-то предпочитает считать в столбик. А кому-то для практики требуются месяца, ребёнок считает разными способами, но ему так и не удаётся научиться считать быстро и без ошибок. Родителям стоит быть терпеливыми, помогать малышу, решать примеры вместе и не злиться. Пусть он чувствует вашу поддержку и заботу. А с регулярной практикой у малыша обязательно все получится.

Источник

Как легко объяснить ребенку сложение и вычитание двузначных чисел?

Содержание статьи:

Обучение детей простым арифметическим действиям – сложный процесс, разделенный на несколько этапов. Сначала изучаются действия с однозначными числами, затем исследуются случаи с переходом через десяток. Когда навык счета в пределах 10 и с переходом через десяток отрабатывается до автоматизма, приступают к изучению сложения и вычитания двузначных чисел. Применение различных методов, проведение занятий в игровой форме помогут малышу понять принцип действий лучше и быстрее.

Подготовительная работа

1. Сначала дети учатся складывать, а затем и вычитать круглые числа.
2. Затем решают примеры, в которых сумма (разность) единиц и десятков не выходит за пределы десяти.
3. Наконец, исследуют случаи с переходом через разряд.

Перед изучением арифметических действий важно научиться делить числа на разрядные слагаемые (25=20+5), определять, из каких разрядных единиц состоит число (25 – 2 десятка и 5 единиц).

При объяснении состава чисел можно использовать практический метод – выкладывание числа с помощью счетных палочек.

• Объясняется, что одна вертикально расположенная палочка – это единица, две – это число 2 и т.д.
• 10 палочек – это десяток. Есть числа, состоящие из нескольких десятков. Для их выкладывания нужно много палочек, да и считать будет трудно. Поэтому десяток будет обозначать горизонтально расположенная палочка (если палочки стандартного размера, то на горизонтальной поместится ровно 10 вертикальных).
• Выкладывается любое двузначное число, например, «25»: 2 палочки положить горизонтально (десятки) и 5 – вертикально (единицы).
• Навык доводится до автоматизма методом неоднократного повторения.
• Закрепляется умение определять состав числа с помощью карточек: ребенок смотрит на число и делит его на разрядные слагаемые или определяет его состав.

Палочки можно заменить деталями Лего или другого конструктора: маленькие будут обозначать единицы, большие – десятки. После отработки навыка приступают к изучению сложения и вычитания круглых чисел.

Сложение и вычитание круглых чисел

• На основе знаний состава чисел: 10+20= 1 десяток + 2 десятка = 3 десятка, или 30.
• С помощью палочек или конструктора: выкладывают 1 горизонтальную палочку, добавляют еще 2, получается 3 – итого, 3 десятка, или 30.

Аналогично объясняется вычитание. Решив несколько примеров, переходят к следующему этапу.

Сложение и вычитание без перехода через разряд

Действия объясняют практическим способом. Например, нужно найти результат выражения «25+32» .

Сначала выкладывают первое число (2 горизонтальных и 5 вертикальных палочек), затем – второе (3 горизонтальных и 2 вертикальных). После этого считают все горизонтальные (складывают десятки – получилось 5), потом – вертикальные (прибавляют единицы – получается 7).

Читают ответ: 57. На основе выполненных действий делают вывод, что единицы складывают с единицами, десятки – с десятками. После отработки действия можно работать уже без палочек.

Если пропустить этап иллюстративного объяснения (а может, даже и «открытия», которое можно сделать, решая пример с помощью палочек) и просто сказать, что складываются единицы одинаковых разрядов, ребенку может оказаться непонятным, почему именно так. Запомнить, как решаются подобные примеры, ему будет сложно.

После объяснения смысла действия можно ввести сложения в столбик.

Полезно будет сначала рассмотреть неверные записи, решить их столбиком и проверить сложением с помощью палочек, а потом уже сделать выводы.

Аналогично вводится вычитание с помощью палочек и в столбик. Если ребенок успешно освоил предыдущий этап, то в этом у него вопросов не возникнет. А через время можно будет переходить на последнюю, самую сложную стадию.

Сложение и вычитание двузначных чисел с переходом через разряд

Сложность выполнения действий заключается в том, что нужно будет «запоминать» числа при сложении и «занимать» при вычитании.

1. Выкладывают числа палочками, складывают разрядные единицы. Получается 5 горизонтальных и 12 вертикальных палочек.
2. Вспоминают, что 10 единиц – это десяток, поэтому их можно заменить одной горизонтальной палочкой.
3. Получается 6 десятков и 2 единицы. Значит, 25+37=62.
4. Делают вывод: при сложении единиц получилось число больше 10, поэтому разделили его на десяток и единицы, а затем определили число. Удобнее сначала складывать единицы (если их будет больше десяти, то можно без особых проблем выделить десяток и добавить его к имеющимся).

• Сначала к числу прибавляют десятки, а потом единицы: 25+37=(25+30)+7=62;
• Первое слагаемое доводят до круглого (25+5=30), потом к нему прибавляют второе (30+37=67) и отнимают столько, сколько добавляли в первом действии (67-5=62);
• Отдельно складываются единицы, отдельно – десятки, а потом – результаты: 25+37=(20+30)+(5+7)=50+12=62.

1. Выкладывают первое число (4 десятка и 2 единицы).
2. Определяют, что из 2 единиц нельзя вычесть 5, поэтому один десяток нужно «перевести» в единицы (заменить десятью вертикальными палочками).
3. Дальнейшие действия: из 12 единиц вычитают 5, получается 7, далее отнимают десятки (желательно проговорить, что было 4, а после преобразования осталось 3).
4. В итоге получается 2 десятка и 7 единиц, или 27. Проверить вычитание нужно с помощью сложения, чтобы убедиться, что решили пример правильно.

• Сначала вычитают десятки, потом – единицы: 42-15=42-10-5=27;
• Наоборот, сначала – единицы, потом – десятки: 42-15=42-5-10=37-10=27.

Для объяснения арифметических действий можно использовать счеты. На них для каждого разряда имеется свое место, поэтому детям будет несложно «записывать» на них числа, а затем производить действия.

Любой метод может быть успешным только в том случае, если его подбирать в соответствии с особенностями ребенка. Ведь одним достаточно объяснить принцип сложения и вычитания с помощью цифр, другие не поймут до тех пор, пока сами не «увидят» решения.

И, конечно, немаловажную роль в освоении любого материала играет систематизация: работать с примерами нужно регулярно в необходимом объеме .

Источник