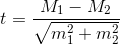- Способы вычисления достоверности различий между двумя независимыми результатами т критерий стьюдента
- Оценка достоверности отличий по t-критерию Стьюдента
- Библиотека постов MEDSTATISTIC об анализе медицинских данных
- Ещё больше полезной информации в нашем блоге в Инстаграм @medstatistic
- Критерии и методы
- t-КРИТЕРИЙ СТЬЮДЕНТА ДЛЯ НЕЗАВИСИМЫХ СОВОКУПНОСТЕЙ
- 1. История разработки t-критерия
- 2. Для чего используется t-критерий Стьюдента?
- 3. В каких случаях можно использовать t-критерий Стьюдента?
- 4. Как рассчитать t-критерий Стьюдента?
- 5. Как интерпретировать значение t-критерия Стьюдента?
- 6. Пример расчета t-критерия Стьюдента
Способы вычисления достоверности различий между двумя независимыми результатами т критерий стьюдента
В большинстве исследований по физической культуре и спорту могут решаться задачи на выявление эффективности той или иной методики обучения и тренировки с применением определенных средств, приемов и способов организации занятий. Решение подобных задач осуществляется путем проведения сравнительного эксперимента с выделением различных групп (экспериментальной и контрольной), результаты которых в теории статистики принято называть независимыми (несвязными). Кроме того, результаты должны быть получены по интервальной шкале или шкале отношений.
В практике в таких случаях наиболее востребованным является t-критерий Стьюдента (псевдоним английского математика В. Госсета).
1. Составить вариационные ряды для результатов контрольных и экспериментальных групп:
| Х | Х | Х | . | Х |
| n | n | n | . | n |
2. Вычислить среднее арифметическое ( для каждой группы в отдельности по формуле:
где — значение отдельного измерения — общее число измерений в группе.
Сопоставление среднеарифметических величин показывает, в какой группе данная величина выше.
Однако для окончательного утверждения того, что занимающиеся экспериментальной группы научились что-то делать лучше, следует убедиться в статистической достоверности различий ( между рассчитанными и .
3. В обеих группах вычислить стандартное отклонение ( ) по следующей формуле:
где — наибольший показатель;
Х — наименьший показатель;
Порядок вычисления стандартного отклонения ( ):
— определить в обеих группах,
— определить Х в обеих группах,
— определить число измерений в каждой группе ( ,
— найти по специальной таблице (табл. 4) значение коэффициента , который соответствует числу измерений в группе,
— подставить полученные значения в формулу и произвести необходимые вычисления.
4. Вычислить стандартные ошибки среднего арифметического значения ( по формулам:
5. Вычислить средние ошибки разности по формуле:
6. По специальной таблице (табл. 5) определить достоверность различий. Для этого полученное значение ( сравнивается с табличным при 5%-ном уровне значимости ( при числе степеней свободы , где и — общее число индивидуальных результатов соответственно в экспериментальной и контрольной группах.
ВЫВОДЫ: Если окажется, что полученное в эксперименте больше табличного значения , то различия между и считаются достоверными при (при 5% уровне значимости). В случае, когда полученное в эксперименте меньше табличного значения , то различия недостоверные , и разница между и имеет случайный характер.
При достоверных различиях между достаточно оснований для того, чтобы говорить о том, что методика в экспериментальной группе оказалась эффективнее методики контрольной группы.
При недостоверных различиях между нет оснований для того, чтобы говорить о том, что методика в экспериментальной группе оказалась эффективнее методики контрольной группы.
Расчеты в ВКР выносятся в приложение, в третьей главе работы приводится сводная таблица сравнительных результатов.
Источник
Оценка достоверности отличий по t-критерию Стьюдента
Наиболее часто в психологическом исследовании встречается задача выявления различий между двумя или более группами признаков. Выявление таких различий на уровне средних арифметических мы уже рассмотрели выше в процедуре анализа первичных статистик. Однако, возникает вопрос насколько эти различия достоверны и можно ли их распространить (экстраполировать) на всю популяцию. Для решения этой задачи чаще всего используется (при условии нормального или близкого к нормальному распределения) t-критерий (или критерий Стьюдента). Этот критерий предназначен для того, чтобы выяснить, на сколько достоверно различаются показатели одной выборки испытуемых от другой (например, когда испытуемые получают в результате тестирования одной группы более высокие баллы, чем представители другой). Это параметрический критерий, имеющий две основные формы. Первая из них — несвязанный t-критерий (который также называют непарным t-критерием) — предназначен для того, чтобы выяснить, имеются ли различия между оценками, полученными при использовании одного и того же теста для тестирования двух групп, составленных из разных людей.
| Например: это может быть сравнение уровня интеллекта или нервно-психической устойчивости, тревожности «успешных» учащихся и «отстающих» или сравнение по этим признакам учащихся разных классов, возрастных групп, социальных уровней и т.д. Это могут быть разнополые, различных национальностей выборки, а также подвыборки в исследуемых выборках, выделенные по определенному признаку. Мы на это указывали, когда говорили о независимых переменных, «L», «Q», и «T»- данных, на основании которых возможно выделение подвыборок в основной выборке исследуемых. |
Критерий называется «несвязанным», потому что сравниваемые группы составлены из разных людей. Связанный t-критерий (который иногда называют парным t-критерием) предназначен для сравнения показателей двух групп, между членами которых существует специфическая связь. Это означает, что каждому члену первой группы соответствует какой-либо член второй группы, который похож на него по какому-то параметру, интересующему исследователя. Чаще всего сравниваются параметры одних и тех же людей до и после определенного события или воздействия (например, в процессе проведения лонгитюдного исследования или формирующего эксперимента). Поэтому данный критерий используется для сравнения показателей одних и тех же людей до и после обследования, эксперимента или прошествии некоторого времени.
В случаях, когда данные не подчиняются нормальному закону распределения, используются непараметрические критерии, эквивалентные t-критериям. Это критерий Манна-Уитни, который эквивалентен непарному t— критерию, и двухвыборочный критерий Вилкоксона, эквивалентный парному t-критерию.
С помощью t-критериев и их непараметрических эквивалентов можно лишь сравнивать результаты двух групп, полученные с использованием одного и того же теста. Однако в некоторых случаях возникает необходимость сравнения нескольких групп или оценок нескольких видов. Это можно сделать поэтапно, разбив задачу на несколько пар сравнений (например, если надо сравнить группы А, Б и В по результатам тестов Х и У, то можно с помощью t-критерия сначала сравнить группы А и Б по результатам теста X, потом А и Б по результатам теста У, А и В по результатам теста Х и так далее). Однако это очень трудоемкий метод; кроме того, по некоторым причинам, в объяснение которых мы не будем здесь углубляться, при его использовании резко возрастает вероятность совершения ошибки первого рода. Поэтому необходим более сложный метод, метод дисперсионного анализа, который требует использования прикладных программ и силу определенной сложности нами не рассматривается
И так, рассмотрим более подробно метод оценки достоверность различий средних арифметических по достаточно эффективному параметрическомукритерию Стьюдента, который предназначен для решения одной из наиболее часто встречающихся задач при обработке данных — выявления достоверности различий между двумя, или более, рядами значений.
Данная оценка часто необходима при сравнительном анализе полярных групп. Эти группы можно выделить, учитывая различную выраженность определенного целевого признака (характеристики) изучаемого явления. Какими критериями при этом руководствоваться мы указывали выше. Обычно анализ начинают с подсчета первичных статистик выделенных групп, затем оценивают достоверность отличий. Он вычисляется по формуле:
Значения критерия Стьюдента для трех уровней доверительной (статистической) значимости (p) приведены в приложении 4. Число степеней свободы определяется по формуле d = v = n1 + n2 — 2, где n и n — объемы сравниваемых выборок. С уменьшением объемов выборок (n «Сортировка» > «Сортировать по …»> «Балл» > ◙ «по возрастанию» (или «убыванию») > ОК. Рисунок 7.17 – Сортировка по шкале «Балл» (Р) Данные отсортированы по возрастанию, начиная от меньшего показателя признака к большему. Затем начинается творческая работа исследователя. Поскольку выборка одна и подчиняется закону нормального распределения признака, то следует в ней определить крайние границы «успешных» и «не успешных» по интеллекту. В целом, можно придерживаться правила, что 50% признаков от средней арифметической составляют популяционную норму, а следовательно, из расчетов должны быть исключены. Однако, в практике эти границы можно варьировать, но в разумных пределах, при определении подвыборок в основной выборке. Выделим в качестве «не успешных» выборку с параметрами P 4 : P 12 (т.е. n1 = 9), а «успешных» — P 24 : P 29 (т.е. n2 = 6). Вычислим для каждой этой выборки отдельно M, σ (S), n, m, придерживаясь алгоритма, указанного раннее для вычисления первичных статистик, используя «Вставку функций» (Рисунок 7.18). Рисунок 7.18 – вычисление первичных статистик по подвыборкам Будьте внимательны! Вы определяете параметры выборок «успешных» и «не успешны» по столбцу «P» («Балл»). Но вычисления будете проводить в столбце первого признака под таблицей – «С». Поэтому параметры выборки «не успешных» будут С 4 : С 12, а «успешных» — С 24: С 29. (см. Рисунок 7.18). После того как вычислены первичные статистики по выборкам «успешных» и «не успешных», переходим к вычислению t-критерия Стьюдента. Алгоритм вычисления t-критерия Стьюдента: Курсор помещаем в ячейку С 45 (см. Рисунок 7.18) и на клавиатуре небираем формулу вычисления t-критерия. Напоминаем как она выглядит и ее вид при введении через клавиатуру в программе Excel.
Обращаем внимание, формула набирается только в английском шрифте, за исключение слова «корень», после чего не забудьте вновь переключиться на английский. Будьте внимательны в соблюденнии знаков и их порядка. С 34 –координаты М1 – «не успешных». С 40 –координаты М2 – «успешных». ^ — показатель степени в которую возводится значение в данной ячейке. Набирается следующим образом: нажимаем одновременно две клавиши «Shift + 6» и появляется значок ^ показателя степени. Затем, набираем квадрат числа – 2. C 37 –координаты m1 – «не успешных». C 43 –координаты m1 – «не успешных». Далее > ОК, появляется вычисленное значение t-критерия для значений признака данного столбца – 3,44. Копируем эту ячейку. Выделяем область втавки по другими сталбцами признаков – «Вставить» > появляются вычисленные значения для других столбцов признаков. Затем обращаемся к таблице «Квантили t-распределения Стьюдента для доверительной вероятности (1-а = 0,95; 0,99; 0,999)» (см. Приложение 4). Вычисляем число степеней свободы по формуле v = d = n1 + n2 – 2,для нашего примера v =6 + 9 – 2 = 13. Выписывем критические значения для p Дата добавления: 2018-06-01 ; просмотров: 27294 ; Мы поможем в написании вашей работы! Источник Библиотека постов MEDSTATISTIC об анализе медицинских данныхЕщё больше полезной информации в нашем блоге в Инстаграм @medstatisticКритерии и методыt-КРИТЕРИЙ СТЬЮДЕНТА ДЛЯ НЕЗАВИСИМЫХ СОВОКУПНОСТЕЙ– общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на распределении Стьюдента. Наиболее частые случаи применения t-критерия связаны с проверкой равенства средних значений в двух выборках. 1. История разработки t-критерияДанный критерий был разработан Уильямом Сили Госсетом для оценки качества пива в компании Гиннесс. В связи с обязательствами перед компанией по неразглашению коммерческой тайны, статья Госсета вышла в 1908 году в журнале «Биометрика» под псевдонимом «Student» (Студент). 2. Для чего используется t-критерий Стьюдента?t-критерий Стьюдента используется для определения статистической значимости различий средних величин. Может применяться как в случаях сравнения независимых выборок (например, группы больных сахарным диабетом и группы здоровых), так и при сравнении связанных совокупностей (например, средняя частота пульса у одних и тех же пациентов до и после приема антиаритмического препарата). В последнем случае рассчитывается парный t-критерий Стьюдента 3. В каких случаях можно использовать t-критерий Стьюдента?Для применения t-критерия Стьюдента необходимо, чтобы исходные данные имели нормальное распределение. Также имеет значение равенство дисперсий (распределения) сравниваемых групп (гомоскедастичность). При неравных дисперсиях применяется t-критерий в модификации Уэлча (Welch’s t). При отсутствии нормального распределения сравниваемых выборок вместо t-критерия Стьюдента используются аналогичные методы непараметрической статистики, среди которых наиболее известными является U-критерий Манна — Уитни. 4. Как рассчитать t-критерий Стьюдента?Для сравнения средних величин t-критерий Стьюдента рассчитывается по следующей формуле: где М1 — средняя арифметическая первой сравниваемой совокупности (группы), М2 — средняя арифметическая второй сравниваемой совокупности (группы), m1 — средняя ошибка первой средней арифметической, m2 — средняя ошибка второй средней арифметической. 5. Как интерпретировать значение t-критерия Стьюдента?Полученное значение t-критерия Стьюдента необходимо правильно интерпретировать. Для этого нам необходимо знать количество исследуемых в каждой группе (n1 и n2). Находим число степеней свободы f по следующей формуле: После этого определяем критическое значение t-критерия Стьюдента для требуемого уровня значимости (например, p=0,05) и при данном числе степеней свободы f по таблице (см. ниже). Сравниваем критическое и рассчитанное значения критерия:
6. Пример расчета t-критерия СтьюдентаДля изучения эффективности нового препарата железа были выбраны две группы пациентов с анемией. В первой группе пациенты в течение двух недель получали новый препарат, а во второй группе — получали плацебо. После этого было проведено измерение уровня гемоглобина в периферической крови. В первой группе средний уровень гемоглобина составил 115,4±1,2 г/л, а во второй — 103,7±2,3 г/л (данные представлены в формате M±m), сравниваемые совокупности имеют нормальное распределение. При этом численность первой группы составила 34, а второй — 40 пациентов. Необходимо сделать вывод о статистической значимости полученных различий и эффективности нового препарата железа. Решение: Для оценки значимости различий используем t-критерий Стьюдента, рассчитываемый как разность средних значений, поделенная на сумму квадратов ошибок: Источник |

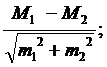 (7.5) где M1 и M2 — значения сравниваемых средних арифметических; t St — величина вычисленного эмпирического критерия, который необходимо сравнивать с критическим; m1 и m2 — соответствующие величины статистических ошибок средних арифметических.
(7.5) где M1 и M2 — значения сравниваемых средних арифметических; t St — величина вычисленного эмпирического критерия, который необходимо сравнивать с критическим; m1 и m2 — соответствующие величины статистических ошибок средних арифметических.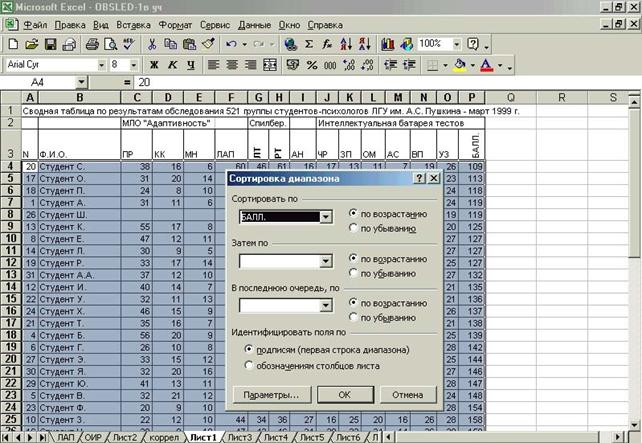
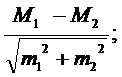
 Уильям Госсет
Уильям Госсет