Способы вычисление координат точек

Координаты точек теодолитного хода: последовательность вычислений

Координаты – это величины, которые отображают местоположение конкретной точки в пространстве. Они определяются путем проведения геодезических измерений, к которым относится триангуляция, а также построение тахеометрического и теодолитного хода.

На плоскости координаты можно вводить неисчислимым количеством способов и через различные математические задачи создавать координатные системы. Благодаря вычислению координаты точек теодолитного хода на карту или план наносятся как эти самые пункты, так и жесткие объекты в зоне их видимости.

Общие понятия о системах координат в геодезии

Столь глубокие познания о строении и форме Земли, которые человек осваивал на протяжении веков, сегодня позволяют создавать невероятно точные координатные системы и картографические проекции.

Координатные системы заданы двумя направлениями на плоскости, а в пространстве – тремя. Осевые направления всегда перпендикулярны друг другу, а ориентированы горизонтально и вертикально. Их пересечение и определяет местоположение точки в заданной системе.

В геодезии координатные системы разделены на следующие две группы:

1. Прямолинейные прямоугольные. К ним причисляют проекцию Гаусса-Крюгера, индивидуальные референцные и местные системы.
2. Полярные. Это геодезические, географические, астрономические, а также геоцентрические и топоцентрические координаты.

Теодолитный ход можно считать самым распространённым плановым обоснованием. Он не требует дорогостоящего и высокоточного оборудования, но помогает создать надежную плановую основу на территориях со сложной местностью. Его развивают от пунктов государственных геодезических сетей (ГГС) и сетей сгущения с уже установленными координатами.

Вычисляются координаты точек замкнутого и разомкнутого теодолитного хода посредством нахождения дирекционных углов его сторон и решения прямой геодезической задачи. Но перед этим следует проверить, соответствуют ли измерения нормативным требованиям.

Исходные данные для расчетов

Теодолитный ход может быть проложен в виде замкнутой фигуры или ломаной линии. Это зависит от характера снимаемой местности. Он является отличной геодезической основой для многих инженерных изысканий.

По итогу проведенных измерений составляется план или карта местности, а все вычисления заносятся в специальные ведомости. В нее заносятся следующие данные:

– горизонтальные углы пунктов;

– измеренное расстояние между ними;

– координаты пункта ГГС или опорной сети;

– значение исходного дирекционного угла.

Для привязки хода к пункту ГГС или опорной сети необходимо определить местоположение одной его точки относительно этого пункта. Это можно сделать, измерив расстояние и горизонтальный примычной угол между ними. Такая процедура называется передачей координат и дирекционных углов.

Уравнивание измерений

Не существует еще методов, позволяющих без погрешностей выполнить измерения, но уравнивание позволит свести их к минимуму. Для замкнутого хода первым делом рассчитывается невязка:

\(\sum \beta _<изм>=\beta _<1>+\beta _<2>+…\beta _\) – сумма углов пунктов;

\(\sum \beta _<теор>\) – теоретическая сумма, определяемая выражением:

\(n\) – количество углов.

Вычисленная невязка допустима, если соответствует требованию:

Когда полученное значение не превышает допуск, то невязку разбрасываются между углами с противоположным знаком равномерно. Можно также распределить ее только между самыми короткими сторонами. Учитывая поправки и их знак, вычисляют исправленные углы:

Правильность уравнивания подтверждается следующим условием:

Поскольку разомкнутый ход является ломаной линией, математические расчеты для него проводятся как для хода, в котором две исходные стороны и дирекционных угла. Для него применяют следующие выражения:

для левых углов:

Для упрощения дальнейших вычислений поправки могут быть распределены с целью округления десятых долей минут в углах до целых минут.

Вычисление дирекционных углов вершин

В геодезии за дирекционный угол (\(\alpha \)) принимают угол, который начинают отсчитывать от северного направления осевого меридиана и до заданной стороны. Он измеряется от 0 до 360°. Вычислить его значение для правой стороны хода можно по формуле ниже:

Для левой стороны это выражение будет иметь такой вид:

\(\alpha _\) – дирекционный угол предыдущей стороны, а \(n\) – последующей;

\(\beta _<пр.исп.>\) – значение правого исправленного угла между сторонами отрезка, а \(\beta _<лев.исп.>\)– левой стороны.

Вычисления выполнены верно при равенстве заданного α и начальной стороны теодолитного хода. Если дирекционный угол больше 360° или имеет отрицательное значение, то это говорит об ошибке в расчетах.

После дирекционных углов необходимо найти румбы – острые углы, отсчитываемые от 0 до 90°. Они берут свое начало от ближайшего окончания осевого меридиана до ориентирной линии.

Четверть румба	Название четверти	Пределы изменения α	Формула румба	Знаки приращения
				ΔХ	ΔУ
I	С.В. (северо-восток)	0° – 90°	r = α	+	+
II	Ю.В. (юго-восток)	90°-180°	r = 180° – α	–	+
III	Ю.З. (юго-запад)	180°-270°	r = α – 180°	–	–
IV	С.З. (северо-запад)	270°-360°	r = 360° – °α	+	–

Таблица 1. Связь дирекционного угла и румба

Вычисление румбов и их знаков приращений зависит от четверти геодезических прямоугольных координат, в которой находится линия ориентирования.

Решение прямой и обратной геодезической задачи

Суть прямой геодезической задачи состоит в том, чтобы определить координатные значения вершины при заданных координатах соседней. Это возможно при известной горизонтальном проложении между ними и дирекционным углом линии. Для ее решения используются следующие формулы:

\(\Delta X=d\cdot cos \alpha \)

\(\Delta Y=d\cdot sin \alpha \)

\(d\)–расстояния между соседними пунктами.

\(\alpha \) – значение дирекционного угла.

Знаки приращений зависят от четверти, определяемой дирекционным углом направления. Координатные значения конечной точки линии равняется сумме координаты начальной и приращения между ними. Из этого следует следующие выражение:

Стоит также упомянуть и обратную геодезическую задачу, которая позволяет определить дирекционный угол, румб и горизонтальное проложение при установленных координатах пунктов теодолитного хода. Вычисления имеют такую последовательность:

определяется румб линии \(r_<1-2>\):

из этого выходит, что:

По знакам приращения определяют четверть, в котором находится направление и по уже известному румбу вычисляют дирекционный угол. Определение горизонтального проложения будет завершающим этапом в решении обратной задачи:

Приращение координат и их увязка

Приращением называют величины, на которые будут увеличены координаты предыдущей точки для вычисления последующей. В основу этих расчетов берется уже знакомая формула прямой задачи:

\(\Delta X=d\cdot cos \alpha \)

\(\Delta Y=d\cdot sin \alpha \)

Полученные значения также необходимо уровнять, чтобы равномерно распределить погрешности и получить наиболее точный результат. Начинают расчеты с определения невязок. Поскольку сумма проекций в сторонах многоугольной замкнутой фигуры равняется нулю, для вычисления невязок пунктов замкнутого хода используют следующую формулу:

\(f_=\sum \Delta X_<выч>-\sum \Delta X_<теор>;\sum \Delta X_<теор>=0\)

\(f_=\sum \Delta Y_<выч>-\sum \Delta Y_<теор>;\sum \Delta Y_<теор>=0\)

\(\sum \Delta X_<выч>,\sum \Delta Y_<выч>\) – суммы приращений, рассчитанные с учетом знаков для замкнутого и разомкнутого хода;

\(\sum \Delta X_<теор>,\sum \Delta Y_<теор>\) – теоретические суммы приращений.

Если невязки не находятся в допуске, необходимы повторные расчеты, чтобы определить ошибку и устранить ее. В противном случае проводятся повторные измерения на участке.

Вследствие влияния погрешностей на ход, он будет разомкнут на величину , которая представляет собой абсолютную невязку в его периметре. По этому причине проверяется соответствие условию допустимости его невязок.

P – периметр хода, полученный суммированием всех его сторон.

Допустимая невязка должна удовлетворять условие 1/2000, а при соответствии выражению \(|f_<отн>|\leq |f_<доп>|\) выполняют ее распределение с противоположным знаком. Однако перед этим рассчитывают поправки приращений, которые определяют для каждой стороны:

\(\delta _>,\delta _>\)– значения поправок в приращениях.

Чтобы упростить дальнейшие расчеты поправки, необходимо округлить их до 0,01 м.

Для разомкнутого хода за теоретическую сумму приращений берется разность между двумя соседними точками.

\(f_=\sum \Delta X_<выч>-\sum \Delta X_<теор>; \sum \Delta X_<теор>=x_-x_\)

\(f_=\sum \Delta Y_<выч>-\sum \Delta Y_<теор>; \sum \Delta Y_<теор>=y_-y_\)

Для обоих ходов поправки имеют противоположный приращению знак. Уравнивание выполнено верно, если сумма исправленных приращений равна или максимально приближена к нулю.

Как вычислить координаты точек хода

Вычисляют значения координат вершин замкнутого и разомкнутого теодолитного хода сначала для опорного пункта, а потом уже для остальных его вершин.

Значение следующего пункта хода вычисляют суммированием предыдущего пункта и исправленного приращения. Это наглядно отображено в формуле:

\(X_,Y_\) – координатные значения предыдущего пункта

В данных формулах применяется алгебраическая сумма, поэтому знаки также необходимо учитывать при расчетах. Если в конце вычислений получены координатные значения начальной точки, то они выполнены правильно.

Нанесение точек на план и его оформление

После завершения обработки измерений, которые были проведены на местности, составляется ее контурный или ситуационный план. Построение плана теодолитного хода происходит поэтапно и состоит из следующих этапов:

1. Создание координатной сетки. Ход необходимо равномерно отобразить на плане, поэтому сначала определяют середину листа. Через весь лист проводят два диагональных отрезка, от которых и будет строиться сетка, состоящая из отрезков по 10 см. Допускается погрешность не более 0,2 мм. Определить их количество можно по формуле:

\(x_,y_\) – наибольшие значения координат, увеличенные до большего значения, которое кратное 200.

\(x_,y_\) – наименьшее значение, но уменьшенное и кратное 200.

200 – длина стороны квадрата в метрах , которая в плане равна 10 см.

1. Обозначение точек на плане. Лучше всего подходят для нанесения координат пунктов на план циркуль и масштабная линейка. Соседние вершины должны иметь такое же расстояние и дирекционный угол, как записано в ведомости.
2. Нанесение ситуации на план. Участки снимаемой местности в процессе полевых работ отображают на специальном схематическом бланке – абрисе. В дальнейшем их используют для переноса контуров, линий и вершин точек. Ситуация изображается на планах и картах специальными обозначениями – условными знаками.
3. Оформление плана в соответствии с требованиями. Все топографические материалы должны строго соответствовать нормативным документам. В частности, нужно выдерживать заданные очертания и их размеры. Должны присутствовать пояснительные надписи, легенда, а также указан масштаб.

Сегодня координаты замкнутого теодолитного хода вычисляются значительно проще, а создание всех графических материалов выполняется при помощи специализированных программ автоматически. Это значительно ускорило процесс выполнения геодезических работ и других инженерных изысканий.

Источник

Как найти координаты точки?

О чем эта статья:

3 класс, 4 класс, 9 класс, 11 класс, ЕГЭ/ОГЭ

Понятие системы координат

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.

Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

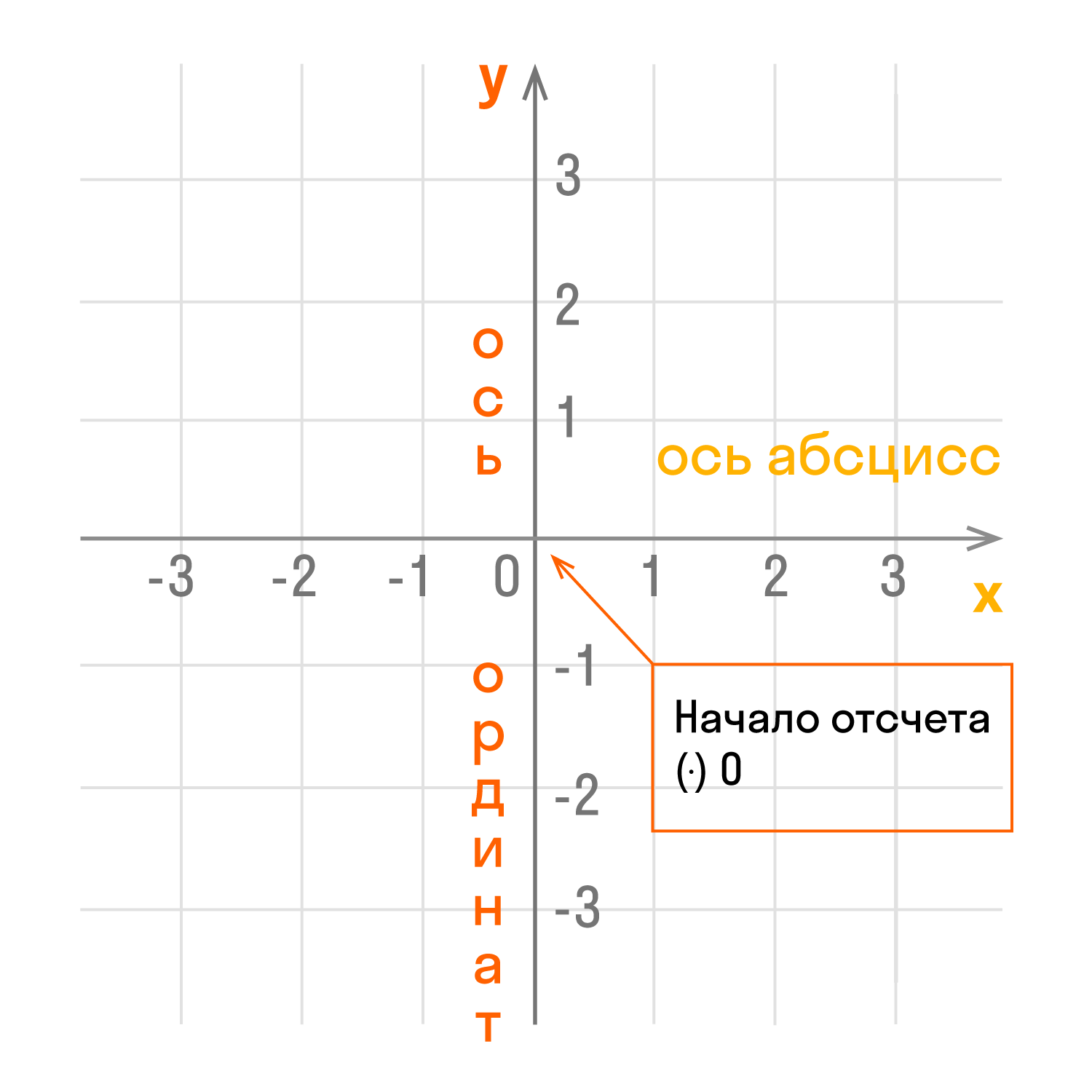
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Читайте также:  Способ обсуждения проблемы 6 букв

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

• Координатные оси — это прямые, образующие систему координат.
• Ось абсцисс Ox — горизонтальная ось.
• Ось ординат Oy — вертикальная ось.
• Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
• Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.

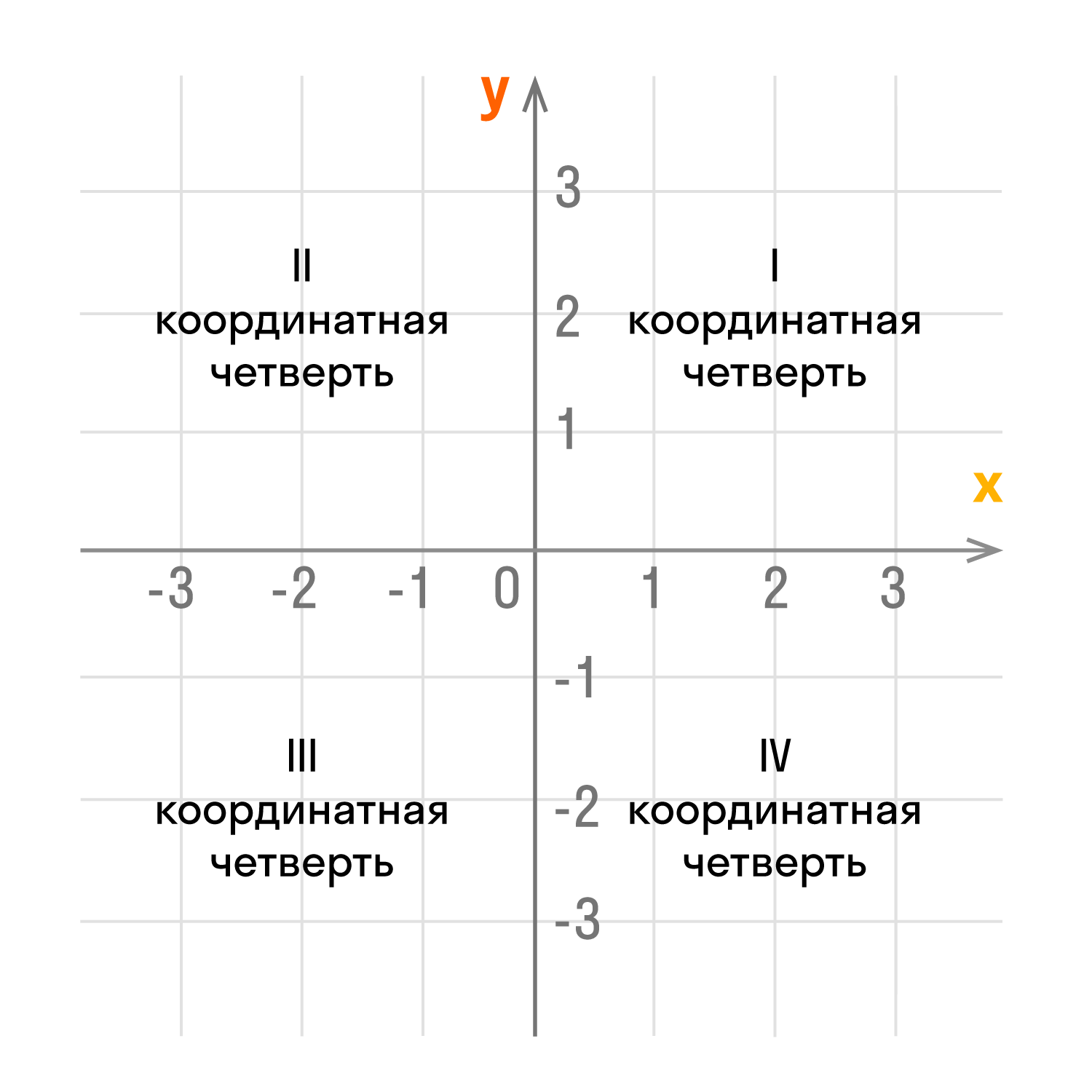
Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

• верхний правый угол — первая четверть I;
• верхний левый угол — вторая четверть II;
• нижний левый угол — третья четверть III;
• нижний правый угол — четвертая четверть IV;

• Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
• Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
• Если обе координаты отрицательны, то число находится в третьей четверти.
• Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.

Определение координат точки

Каждой точке координатной плоскости соответствуют две координаты.

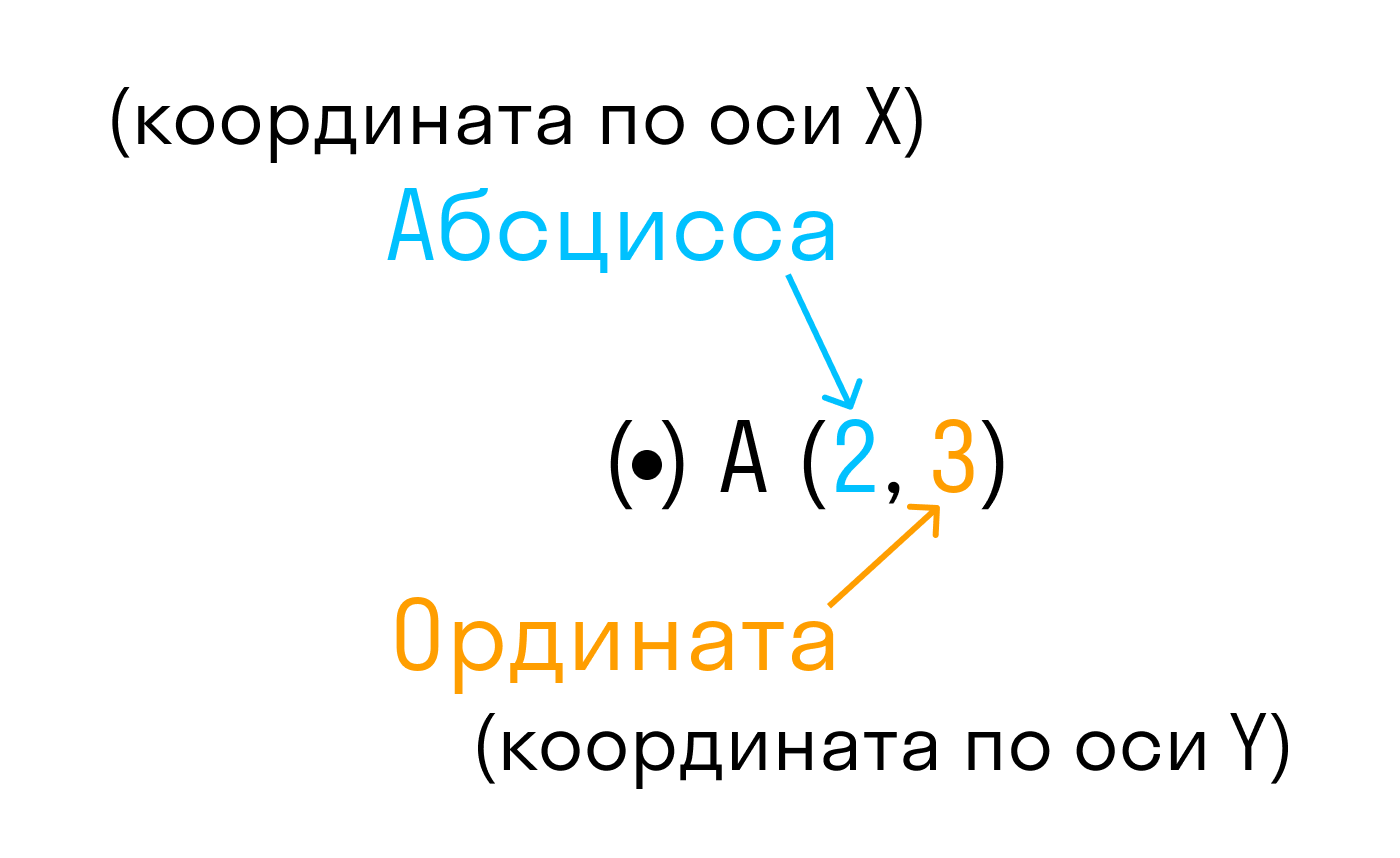
Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.

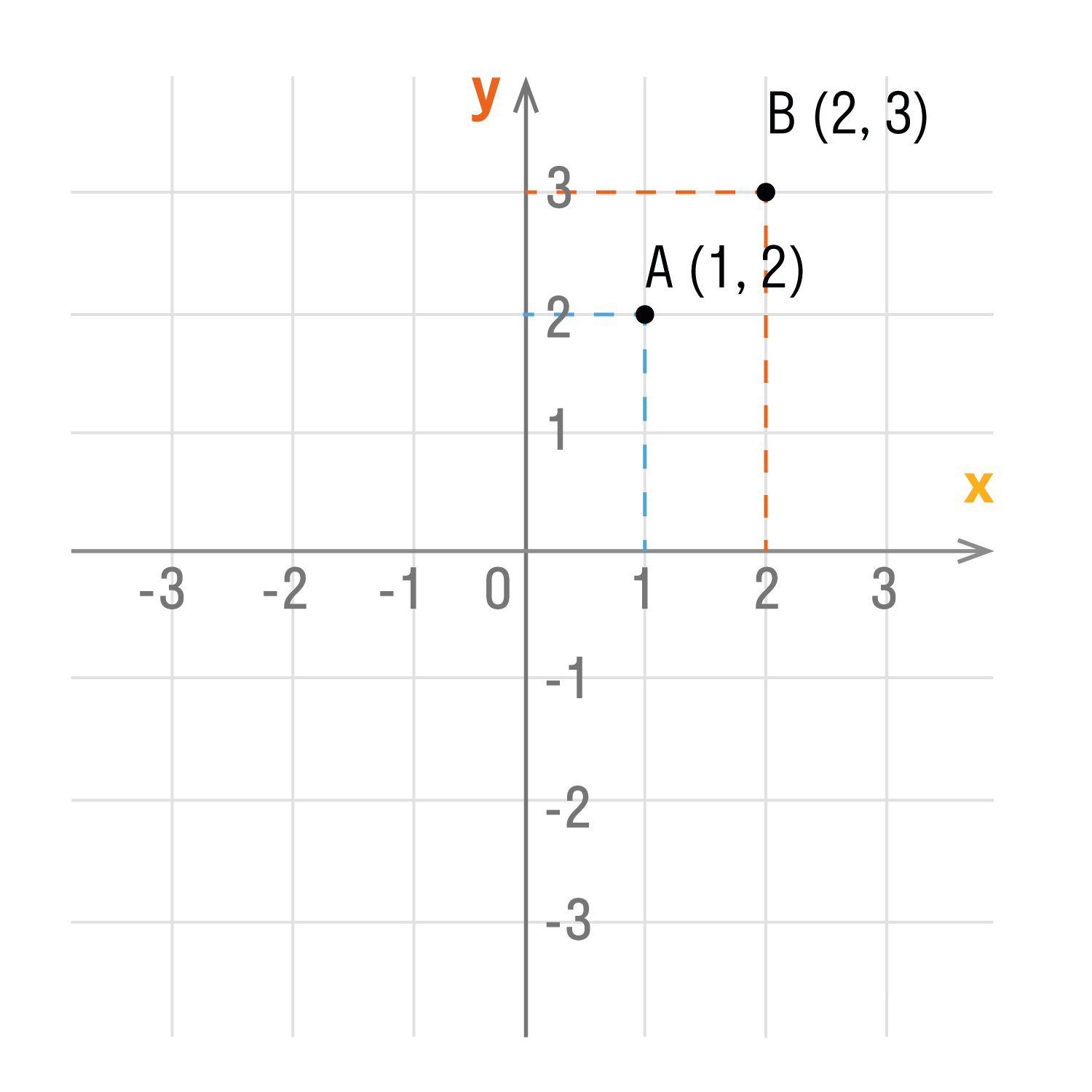
Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.

Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.

Смотрим на график и фиксируем: A (1; 2) и B (2; 3).

Особые случаи расположения точек

В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:

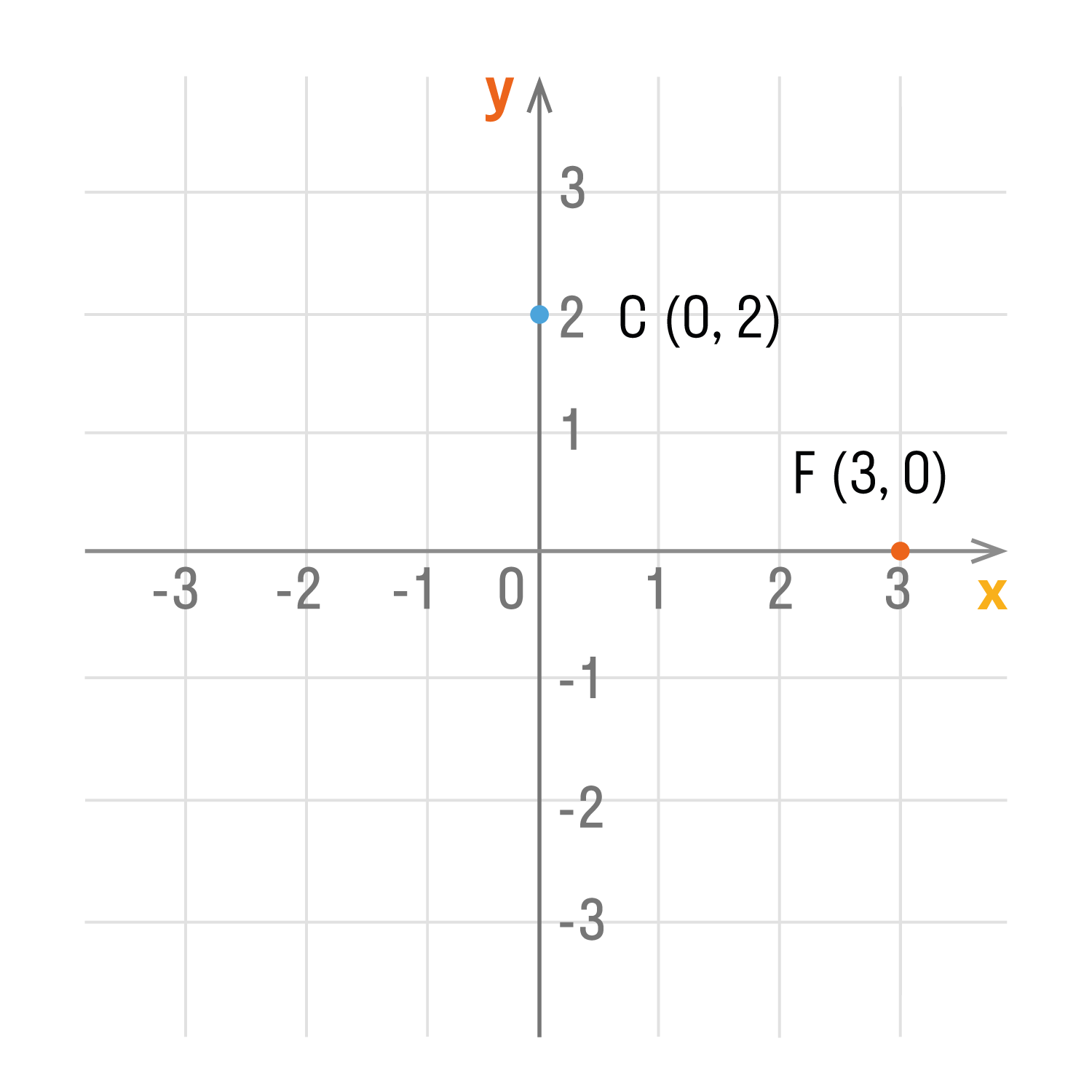
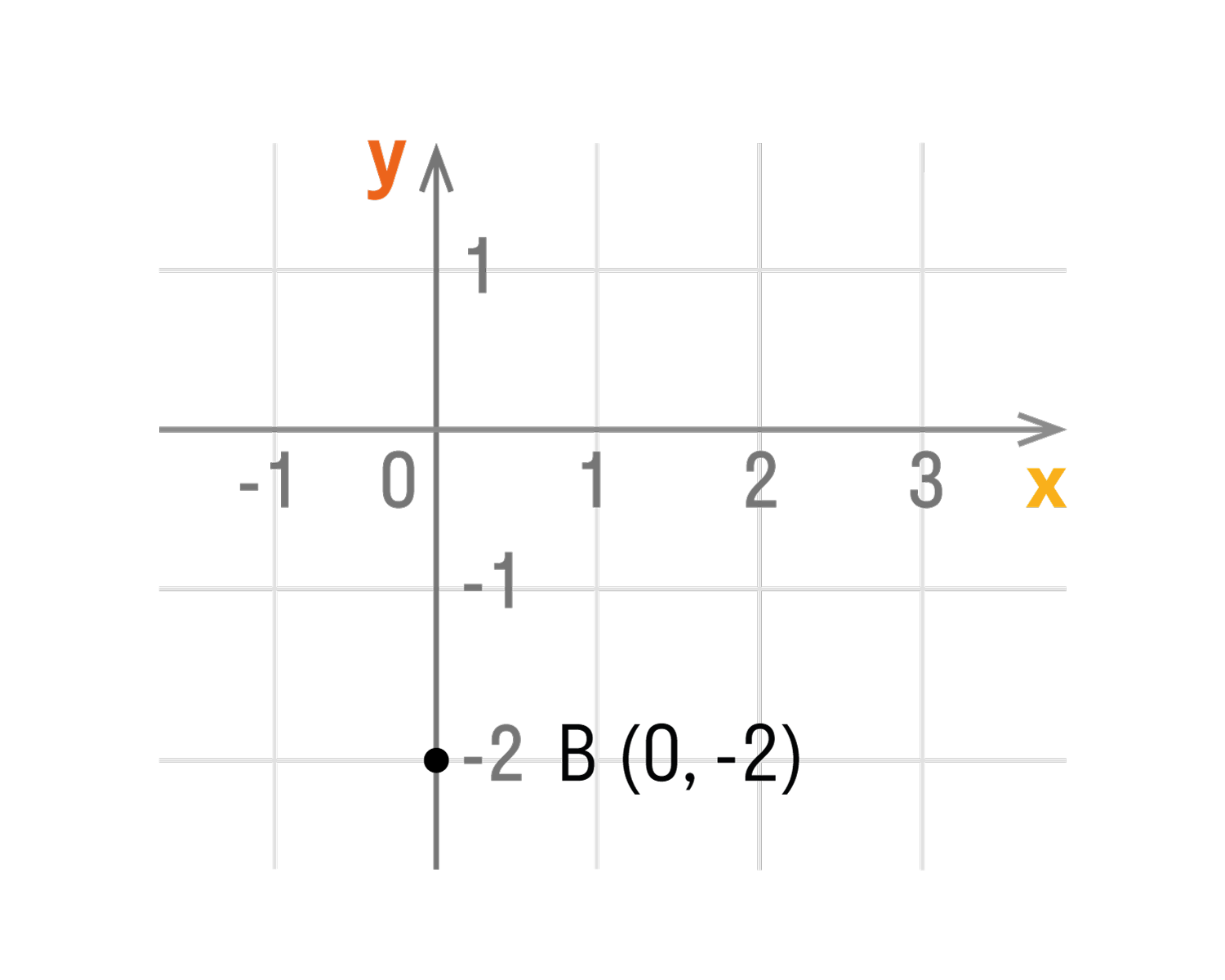
1. Если точка лежит на оси Oy, то ее абсцисса равна 0. Например,
   точка С (0, 2).
2. Если точка лежит на оси Ox, то ее ордината равна 0. Например,
   точка F (3, 0).
3. Начало координат — точка O. Ее координаты равны нулю: O (0,0).
   
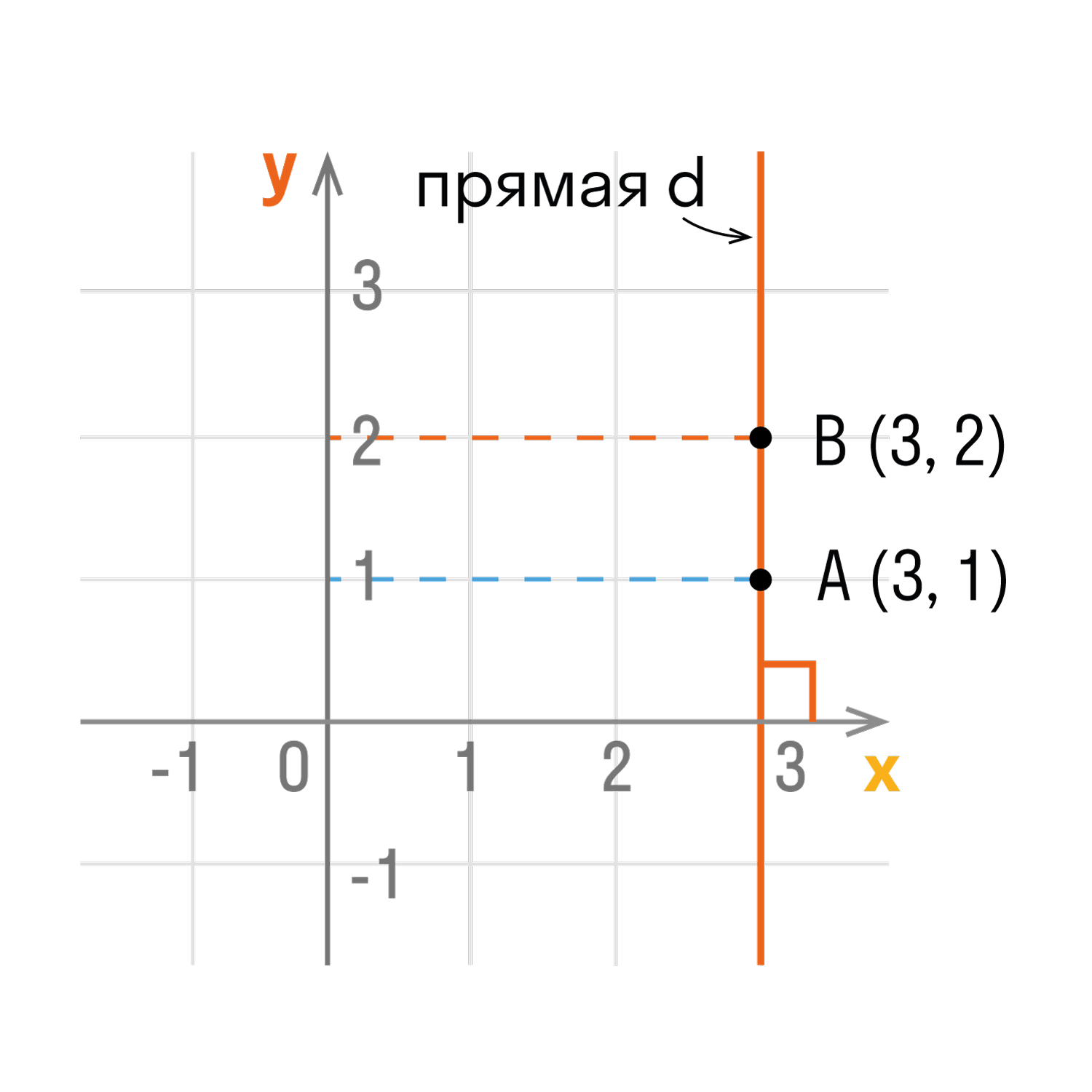
4. Точки любой прямой, которая перпендикулярна оси абсцисс, имеют одинаковые абсциссы.
   
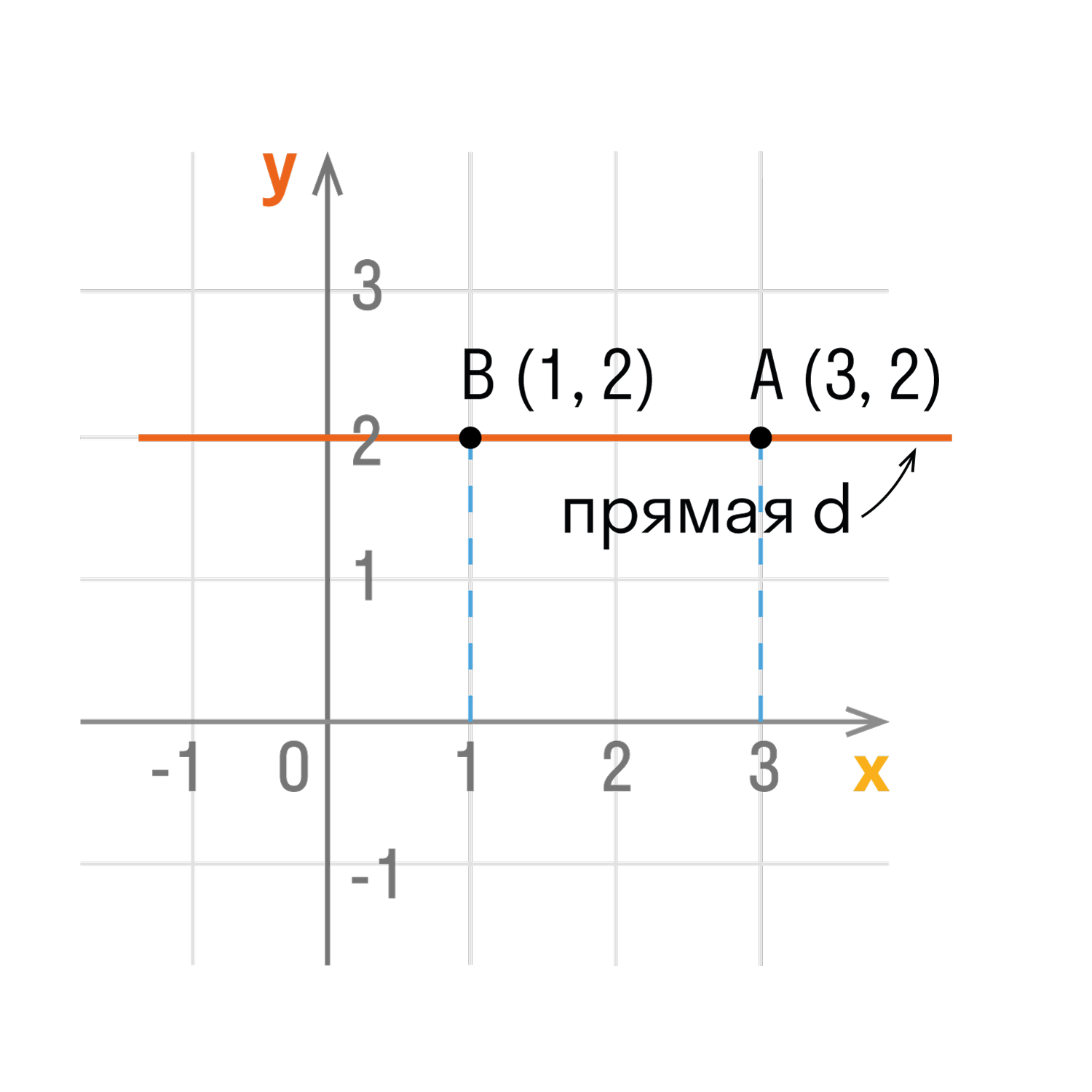
5. Точки любой прямой, которая перпендикулярна оси ординат, имеют одинаковые ординаты.
   
6. Если точка лежит на оси абсцисс, то ее координаты будут иметь вид: (x, 0).
   
7. Если точка лежит на оси ординат, то ее координаты будут иметь вид: (0, y).
   

Способы нахождения точки по её координатам

Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.

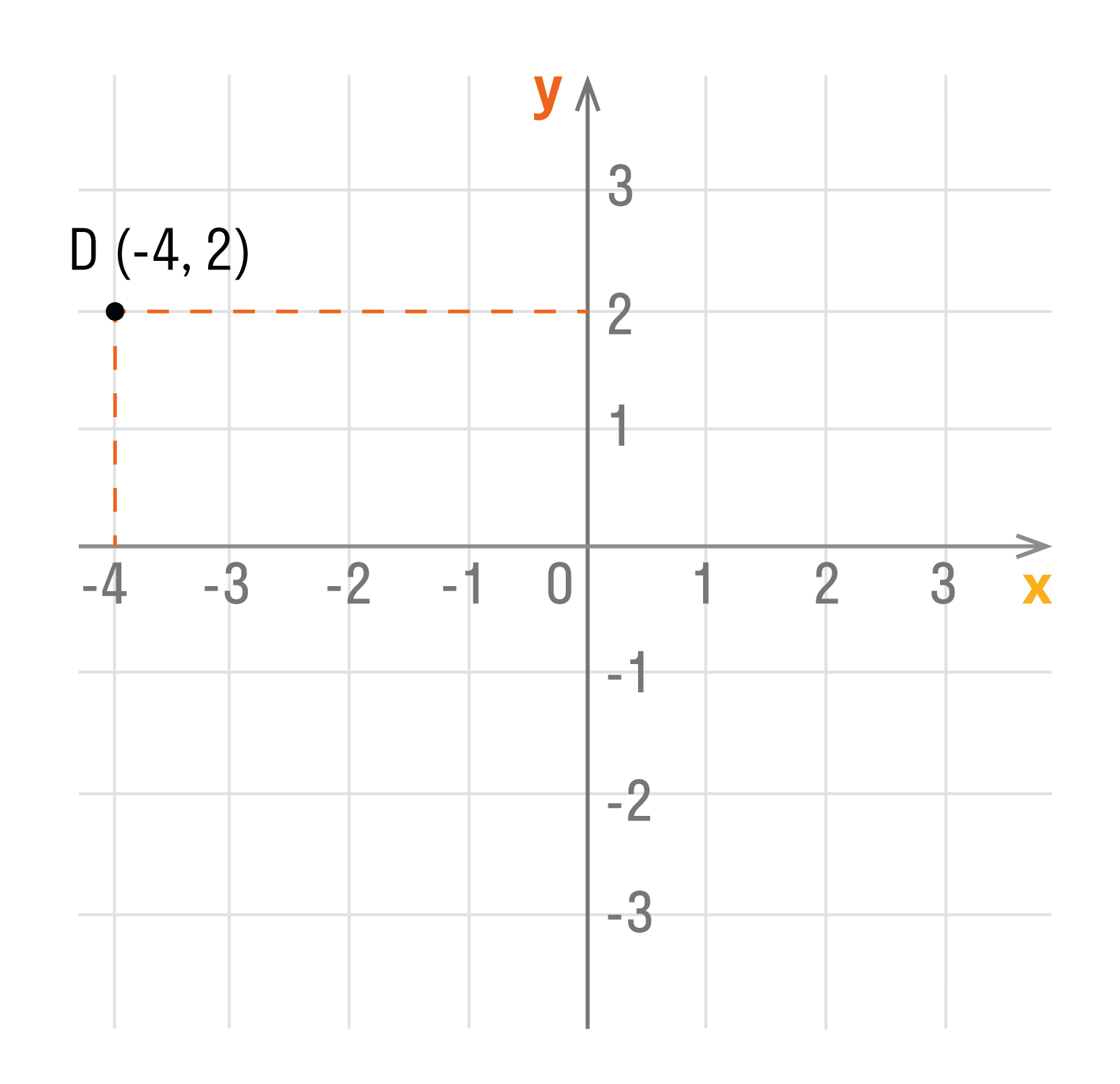
Способ первый. Как определить положение точки D по её координатам (-4, 2):

1. Отметить на оси Ox, точку с координатой -4, и провести через нее прямую перпендикулярную оси Ox.
2. Отметить на оси Oy, точку с координатой 2, и провести через нее прямую перпендикулярную оси Oy.
3. Точка пересечения перпендикуляров и есть искомая точка D. Ее абсцисса равна -4, а ордината — 2.
   

Способ второй. Как определить положение точки D (-4, 2):

1. Сместить прямую по оси Ox влево на 4 единицы, так как у нас
   перед 4 стоит знак минус.
2. Подняться из этой точки параллельно оси Oy вверх на 2 единицы, так как у нас перед 2 стоит знак плюс.
   

Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:

Источник