Эмпирическая функция распределения
Эмпирической (опытной) функцией распределения или функцией распределения выборки называют такую функцию, которая определяет для каждого значения x частоту событий X
Дана таблица функции распределения выборки. Требуется построить эмпирическую функцию распределения
| xi | 1 | 2 | 3 | 4 | 5 | 6 |
| ni | 4 | 10 | 6 | 8 | 7 | 5 |
Из таблицы n=40, т.е.
n=4+10+6+8+7+5=40
Вычислим функцию распределения выборки
Эмпирическая функция распределения имеет вид
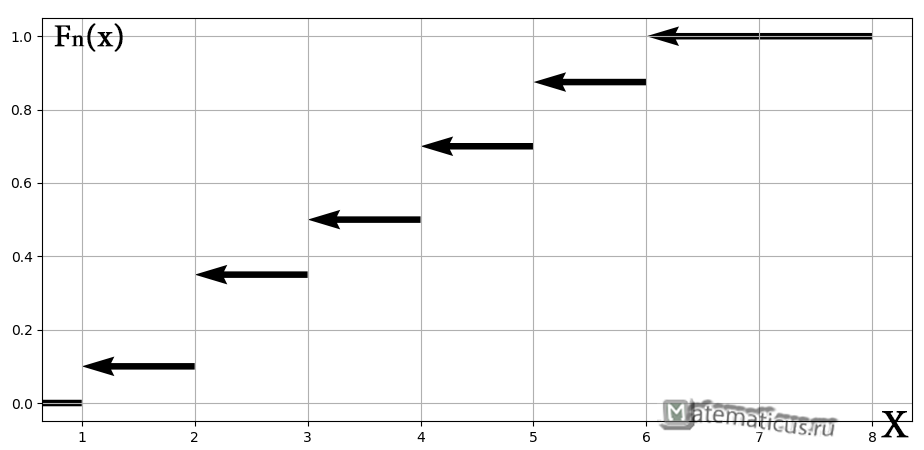
Построим график кусочно-постоянной эмпирической функции распределения
таким образом, по данным выборки можно приближенно построить функцию для неизвестной функции выборки.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.7 / 5. Количество оценок: 33
Оценок пока нет. Поставьте оценку первым.
2 комментария
У вас опечатка, где вы написали n=30, n=4+10+6+8+7+5=30 и F_30, так как n=40.
Исправили. Спасибо Вам большое за внимательность)
Источник
Способы выборки эмпирическая функция распределения
1. Задачи математической статистики.
3. Способы отбора.
4. Статистическое распределение выборки.
5. Эмпирическая функция распределения.
6. Полигон и гистограмма.
7. Числовые характеристики вариационного ряда.
8. Статистические оценки параметров распределения.
9. Интервальные оценки параметров распределения.
1. Задачи и методы математической статистики
Математическая статистика — это раздел математики, посвященный методам сбора, анализа и обработки результатов статистических данных наблюдений для научных и практических целей.
Пусть требуется изучить совокупность однородных объектов относительно некоторого качественного или количественного признака, характеризующего эти объекты. Например, если имеется партия деталей, то качественным признаком может служить стандартность детали, а количественным- контролируемый размер детали.
Иногда проводят сплошное исследование, т.е. обследуют каждый объект относительно нужного признака. На практике сплошное обследование применяется редко. Например, если совокупность содержит очень большое число объектов, то провести сплошное обследование физически невозможно. Если обследование объекта связано с его уничтожением или требует больших материальных затрат, то проводить сплошное обследование не имеет смысла. В таких случаях случайно отбирают из всей совокупности ограниченное число объектов (выборочную совокупность) и подвергают их изучению.
Основная задача математической статистики заключается в исследовании всей совокупности по выборочным данным в зависимости от поставленной цели, т.е. изучение вероятностных свойств совокупности: закона распределения, числовых характеристик и т.д. для принятия управленческих решений в условиях неопределенности.
Генеральная совокупность – это совокупность объектов, из которой производится выборка.
Выборочная совокупность (выборка) – это совокупность случайно отобранных объектов.
Объем совокупности – это число объектов этой совокупности. Объем генеральной совокупности обозначается N , выборочной – n .
Если из 1000 деталей отобрано для обследования 100 деталей, то объем генеральной совокупности N = 1000, а объем выборки n = 100.
При составлении выборки можно поступить двумя способами: после того, как объект отобран и над ним произведено наблюдение, он может быть возвращен либо не возвращен в генеральную совокупность. Т.о. выборки делятся на повторные и бесповторные.
Повторной называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность.
Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается.
На практике обычно пользуются бесповторным случайным отбором.
Для того, чтобы по данным выборки можно было достаточно уверенно судить об интересующем признаке генеральной совокупности, необходимо, чтобы объекты выборки правильно его представляли. Выборка должна правильно представлять пропорции генеральной совокупности. Выборка должна быть репрезентативной (представительной).
В силу закона больших чисел можно утверждать, что выборка будет репрезентативной, если ее осуществлять случайно.
Если объем генеральной совокупности достаточно велик, а выборка составляет лишь незначительную часть этой совокупности, то различие между повторной и бесповторной выборками стирается; в предельном случае, когда рассматривается бесконечная генеральная совокупность, а выборка имеет конечный объем, это различие исчезает.
В американском журнале «Литературное обозрение» с помощью статистических методов было проведено исследование прогнозов относительно исхода предстоящих выборов президента США в 1936 году. Претендентами на этот пост были Ф.Д. Рузвельт и А. М. Ландон. В качестве источника для генеральной совокупности исследуемых американцев были взяты справочники телефонных абонентов. Из них случайным образом были выбраны 4 миллиона адресов., по которым редакция журнала разослала открытки с просьбой высказать свое отношение к кандидатам на пост президента. Обработав результаты опроса, журнал опубликовал социологический прогноз о том, что на предстоящих выборах с большим перевесом победит Ландон. И … ошибся: победу одержал Рузвельт.
Этот пример можно рассматривать, как пример нерепрезентативной выборки. Дело в том, что в США в первой половине двадцатого века телефоны имела лишь зажиточная часть населения, которые поддерживали взгляды Ландона.
На практике применяются различные способы отбора, которые можно разделить на 2 вида:
1. Отбор не требует расчленения генеральной совокупности на части (а) простой случайный бесповторный; б) простой случайный повторный).
2. Отбор, при котором генеральная совокупность разбивается на части. (а) типичный отбор; б) механический отбор; в) серийный отбор).
Простым случайным называют такой отбор, при котором объекты извлекаются по одному из всей генеральной совокупности (случайно).
Типичным называют отбор, при котором объекты отбираются не из всей генеральной совокупности, а из каждой ее «типичной» части. Например, если деталь изготавливают на нескольких станках, то отбор производят не из всей совокупности деталей, произведенных всеми станками, а из продукции каждого станка в отдельности. Таким отбором пользуются тогда, когда обследуемый признак заметно колеблется в различных «типичных» частях генеральной совокупности.
Механическим называют отбор, при котором генеральную совокупность «механически» делят на столько групп, сколько объектов должно войти в выборку, а из каждой группы отбирают один объект. Например, если нужно отобрать 20 % изготовленных станком деталей, то отбирают каждую 5-ую деталь; если требуется отобрать 5 % деталей- каждую 20-ую и т.д. Иногда такой отбор может не обеспечивать репрезентативность выборки (если отбирают каждый 20-ый обтачиваемый валик, причем сразу же после отбора производится замена резца, то отобранными окажутся все валики, обточенные затупленными резцами).
Серийным называют отбор, при котором объекты отбирают из генеральной совокупности не по одному, а «сериями», которые подвергают сплошному обследованию. Например, если изделия изготавливаются большой группой станков-автоматов, то подвергают сплошному обследованию продукцию только нескольких станков.
На практике часто применяют комбинированный отбор, при котором сочетаются указанные выше способы.
4. Статистическое распределение выборки
Пусть из генеральной совокупности извлечена выборка, причем значение x1 –наблюдалось раз, x2-n2 раз,… xk — nk раз. n = n1+n2+. +nk– объем выборки. Наблюдаемые значения называются вариантами, а последовательность вариант, записанных в возрастающем порядке- вариационным рядом. Числа наблюдений называются частотами (абсолютными частотами), а их отношения к объему выборки — относительными частотами или статистическими вероятностями.
Если количество вариант велико или выборка производится из непрерывной генеральной совокупности, то вариационный ряд составляется не по отдельным точечным значениям, а по интервалам значений генеральной совокупности. Такой вариационный ряд называется интервальным. Длины интервалов при этом должны быть равны.
Статистическим распределением выборки называется перечень вариант и соответствующих им частот или относительных частот.
Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (суммы частот, попавших в этот интервал значений)
Точечный вариационный ряд частот может быть представлен таблицей:
Источник
Способы выборки эмпирическая функция распределения
рПУЛПМШЛХ ОЕЙЪЧЕУФОПЕ ТБУРТЕДЕМЕОЙЕ НПЦОП ПРЙУБФШ, ОБРТЙНЕТ, ЕЗП ЖХОЛГЙЕК ТБУРТЕДЕМЕОЙС , РПУФТПЙН РП ЧЩВПТЛЕ «ПГЕОЛХ» ДМС ЬФПК ЖХОЛГЙЙ.
ьНРЙТЙЮЕУЛПК ЖХОЛГЙЕК ТБУРТЕДЕМЕОЙС, РПУФТПЕООПК РП ЧЩВПТЛЕ ПВЯЕНБ , ОБЪЩЧБЕФУС УМХЮБКОБС ЖХОЛГЙС , РТЙ ЛБЦДПН ТБЧОБС
ОБЪЩЧБЕФУС ЙОДЙЛБФПТПН УПВЩФЙС . рТЙ ЛБЦДПН ЬФП УМХЮБКОБС ЧЕМЙЮЙОБ, ЙНЕАЭБС ТБУРТЕДЕМЕОЙЕ вЕТОХММЙ У РБТБНЕФТПН . РПЮЕНХ?
йОБЮЕ ЗПЧПТС, РТЙ МАВПН ЪОБЮЕОЙЕ , ТБЧОПЕ ЙУФЙООПК ЧЕТПСФОПУФЙ УМХЮБКОПК ЧЕМЙЮЙОЕ ВЩФШ НЕОШЫЕ , ПГЕОЙЧБЕФУС ДПМЕК ЬМЕНЕОФПЧ ЧЩВПТЛЙ, НЕОШЫЙИ .
еУМЙ ЬМЕНЕОФЩ ЧЩВПТЛЙ , , ХРПТСДПЮЙФШ РП ЧПЪТБУФБОЙА (ОБ ЛБЦДПН ЬМЕНЕОФБТОПН ЙУИПДЕ), РПМХЮЙФУС ОПЧЩК ОБВПТ УМХЮБКОЩИ ЧЕМЙЮЙО, ОБЪЩЧБЕНЩК ЧБТЙБГЙПООЩН ТСДПН :
ьМЕНЕОФ , , ОБЪЩЧБЕФУС -Н ЮМЕОПН ЧБТЙБГЙПООПЗП ТСДБ ЙМЙ -К РПТСДЛПЧПК УФБФЙУФЙЛПК .
чЩВПТЛБ:
чБТЙБГЙПООЩК ТСД:
ьНРЙТЙЮЕУЛБС ЖХОЛГЙС ТБУРТЕДЕМЕОЙС ЙНЕЕФ УЛБЮЛЙ Ч ФПЮЛБИ ЧЩВПТЛЙ, ЧЕМЙЮЙОБ УЛБЮЛБ Ч ФПЮЛЕ ТБЧОБ , ЗДЕ ЛПМЙЮЕУФЧП ЬМЕНЕОФПЧ ЧЩВПТЛЙ, УПЧРБДБАЭЙИ У .
нПЦОП РПУФТПЙФШ ЬНРЙТЙЮЕУЛХА ЖХОЛГЙА ТБУРТЕДЕМЕОЙС РП ЧБТЙБГЙПООПНХ ТСДХ:
дТХЗПК ИБТБЛФЕТЙУФЙЛПК ТБУРТЕДЕМЕОЙС СЧМСЕФУС ФБВМЙГБ (ДМС ДЙУЛТЕФОЩИ ТБУРТЕДЕМЕОЙК) ЙМЙ РМПФОПУФШ (ДМС БВУПМАФОП ОЕРТЕТЩЧОЩИ). ьНРЙТЙЮЕУЛЙН, ЙМЙ ЧЩВПТПЮОЩН БОБМПЗПН ФБВМЙГЩ ЙМЙ РМПФОПУФЙ СЧМСЕФУС ФБЛ ОБЪЩЧБЕНБС ЗЙУФПЗТБННБ .
зЙУФПЗТБННБ УФТПЙФУС РП ЗТХРРЙТПЧБООЩН ДБООЩН. рТЕДРПМБЗБЕНХА ПВМБУФШ ЪОБЮЕОЙК УМХЮБКОПК ЧЕМЙЮЙОЩ (ЙМЙ ПВМБУФШ ЧЩВПТПЮОЩИ ДБООЩИ) ДЕМСФ ОЕЪБЧЙУЙНП ПФ ЧЩВПТЛЙ ОБ ОЕЛПФПТПЕ ЛПМЙЮЕУФЧП ЙОФЕТЧБМПЧ (ОЕ ПВСЪБФЕМШОП ПДЙОБЛПЧЩИ). рХУФШ , , ЙОФЕТЧБМЩ ОБ РТСНПК, ОБЪЩЧБЕНЩЕ ЙОФЕТЧБМБНЙ ЗТХРРЙТПЧЛЙ . пВПЪОБЮЙН ДМС ЮЕТЕЪ ЮЙУМП ЬМЕНЕОФПЧ ЧЩВПТЛЙ, РПРБЧЫЙИ Ч ЙОФЕТЧБМ :
оБ ЛБЦДПН ЙЪ ЙОФЕТЧБМПЧ УФТПСФ РТСНПХЗПМШОЙЛ, РМПЭБДШ ЛПФПТПЗП РТПРПТГЙПОБМШОБ . пВЭБС РМПЭБДШ ЧУЕИ РТСНПХЗПМШОЙЛПЧ ДПМЦОБ ТБЧОСФШУС ЕДЙОЙГЕ. рХУФШ ДМЙОБ ЙОФЕТЧБМБ . чЩУПФБ РТСНПХЗПМШОЙЛБ ОБД ТБЧОБ
рПМХЮЕООБС ЖЙЗХТБ ОБЪЩЧБЕФУС ЗЙУФПЗТБННПК.
йНЕЕФУС ЧБТЙБГЙПООЩК ТСД (УН. РТЙНЕТ 1):
тБЪПВШЕН ПФТЕЪПЛ ОБ 4 ТБЧОЩИ ПФТЕЪЛБ. ч ПФТЕЪПЛ РПРБМЙ 4 ЬМЕНЕОФБ ЧЩВПТЛЙ, Ч 6, Ч 3, Й Ч ПФТЕЪПЛ РПРБМЙ 2 ЬМЕНЕОФБ ЧЩВПТЛЙ. уФТПЙН ЗЙУФПЗТБННХ (ТЙУ. 2). оБ ТЙУ. 3 ФПЦЕ ЗЙУФПЗТБННБ ДМС ФПК ЦЕ ЧЩВПТЛЙ, ОП РТЙ ТБЪВЙЕОЙЙ ПВМБУФЙ ОБ 5 ТБЧОЩИ ПФТЕЪЛПЧ.
| тЙУ. 2. рТЙНЕТ 2 | тЙУ. 3. рТЙНЕТ 2 | |
| ч ЛХТУЕ «ьЛПОПНЕФТЙЛБ» ХФЧЕТЦДБЕФУС, ЮФП ОБЙМХЮЫЙН ЮЙУМПН ЙОФЕТЧБМПЧ ЗТХРРЙТПЧЛЙ («ЖПТНХМБ уФЕТДЦЕУУБ») СЧМСЕФУС . ъДЕУШ ДЕУСФЙЮОЩК МПЗБТЙЖН, РПЬФПНХ , Ф.Е. РТЙ ХЧЕМЙЮЕОЙЙ ЧЩВПТЛЙ ЧДЧПЕ ЮЙУМП ЙОФЕТЧБМПЧ ЗТХРРЙТПЧЛЙ ХЧЕМЙЮЙЧБЕФУС ОБ 1. ъБНЕФЙН, ЮФП ЮЕН ВПМШЫЕ ЙОФЕТЧБМПЧ ЗТХРРЙТПЧЛЙ, ФЕН МХЮЫЕ. оП, ЕУМЙ ВТБФШ ЮЙУМП ЙОФЕТЧБМПЧ, УЛБЦЕН, РПТСДЛБ , ФП У ТПУФПН ЗЙУФПЗТБННБ ОЕ ВХДЕФ РТЙВМЙЦБФШУС Л РМПФОПУФЙ. уРТБЧЕДМЙЧП УМЕДХАЭЕЕ ХФЧЕТЦДЕОЙЕ: еУМЙ РМПФОПУФШ ТБУРТЕДЕМЕОЙС ЬМЕНЕОФПЧ ЧЩВПТЛЙ СЧМСЕФУС ОЕРТЕТЩЧОПК ЖХОЛГЙЕК, ФП РТЙ ФБЛ, ЮФП , ЙНЕЕФ НЕУФП РПФПЮЕЮОБС УИПДЙНПУФШ РП ЧЕТПСФОПУФЙ ЗЙУФПЗТБННЩ Л РМПФОПУФЙ. фБЛ ЮФП ЧЩВПТ МПЗБТЙЖНБ ТБЪХНЕО, ОП ОЕ СЧМСЕФУС ЕДЙОУФЧЕООП ЧПЪНПЦОЩН. Источник Статистическое распределение выборки. Эмпирическая функция распределенияРаздел второй Математическая статистика Глава 1. Выборочный метод Выборочная и генеральная совокупности. Типы выборок Под генеральной совокупностью понимают множество всех объектов некоторого наблюдения в совокупности с множеством всех значений этого наблюдения, соответствующих каждому объекту. Под выборкой объема n понимают множество из n объектов, реально подвергшихся наблюдению, в совокупности с n значениями наблюдения для каждого объекта. Например, генеральная совокупность – группа студентов, присутствующих на паре; выборка объема n – n студентов, опрошенных преподавателем, вместе с оценками, полученными ими. Основная задача статистики – получить обоснованные выводы о свойствах генеральной совокупности, анализируя, извлеченную из нее выборку. Для того чтобы по данным выборки можно было достаточно уверенно судить об интересующем признаке генеральной совокупности, необходимо, чтобы выборка была репрезентативной (представительной), то есть достаточно полно представлять изучаемые признаки генеральной совокупности. Условием обеспечения репрезентативности выборки является, согласно закону больших чисел, соблюдение случайности отбора, то есть все объекты имеют одинаковую вероятность попасть в выборку. Повторной называют выборку, при которой отобранный объект перед извлечением следующего возвращается в генеральную совокупность. Бесповторной называют выборку, при которой На практике чаще используется безповторная выборка. Статистическое распределение выборки. Эмпирическая функция распределения Пусть из генеральной совокупности извлечена выборка, причем значение признака х1наблюдалось п1 раз, х2 – п2 раз, и т.д., хk – пk раз и Статистическим распределением выборки (статистическим рядом) называют перечень вариант и соответствующихим частот или относительных частот. Записывается статистическое распределение в виде таблицы. Первая строка содержит варианты хi, а вторая – их частоты Статистическое распределение выборки является оценкой неизвестного распределения. При больших значениях Накопленной частотой Относительные накопленные частоты – это статистические аналоги значений функции распределения Эмпирической (статистической) функцией распределения выборки называется функция В отличие от эмпирической функции распределения выборки функцию распределения F(х) генеральной совокупности называют теоретической функцией распределения. Различие между эмпирической и теоретической функциями состоит в том, что теоретическая функция F(х)определяет вероятность события <Х Источник | ||

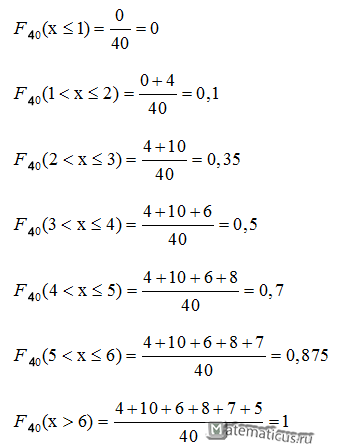

 – объему выборки. Наблюдаемые значения хi называют вариантами, а последовательность вариант, записанных в возрастающем порядке, – вариационным рядом. Операции расположения вариант по неубыванию называется ранжированием статистических данных. Числа наблюдений
– объему выборки. Наблюдаемые значения хi называют вариантами, а последовательность вариант, записанных в возрастающем порядке, – вариационным рядом. Операции расположения вариант по неубыванию называется ранжированием статистических данных. Числа наблюдений  называют частотами,а их отношения к объему выборки
называют частотами,а их отношения к объему выборки  – относительными частотами. Причем
– относительными частотами. Причем  .
. ).
).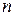 статистическое распределение мало отличается от истинного распределения.
статистическое распределение мало отличается от истинного распределения. называется число вариант выборки меньших данного числа х, а их отношения к объему выборки
называется число вариант выборки меньших данного числа х, а их отношения к объему выборки  – относительной накопленной частотой. Ясно, что
– относительной накопленной частотой. Ясно, что  , так как нет ни одной варианты, меньшей х1. Кроме того,
, так как нет ни одной варианты, меньшей х1. Кроме того, 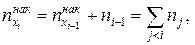
 .
. дискретной случайной величины.
дискретной случайной величины. , определяющая для каждого значения х относительную накопленную частоту, то есть
, определяющая для каждого значения х относительную накопленную частоту, то есть 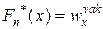 .
.


