Способы выбора стандартного состояния компонента раствора

§ 2. Выбор стандартного состояния

Для растворов разных типов удобно выбирать и различные состояния в качестве стандартных. Начнем с растворов, близких к совершенным.

Вообще стандартное состояние следует выбирать так, чтобы в условиях, когда поведение реального раствора становится таким же, как идеального, активность совпадала бы с концентрацией и сохранилась бы форма уравнений, характеризующих термодинамические свойства идеальных растворов.

Для совершенных растворов p_i = p

0

i

x_i или x_i = p_i/p

0

i

.

Сопоставление этого соотношения с уравнением (VI.2) показывает, что активность может совпадать с молярной долей в случае p

ст

i

Таким образом, для растворов, близких к совершенным, в качестве стандартного состояния принимается чистый компонент, и в этом случае

a_i = p_i/p

0

i

(VI.3)

Отсюда ясно, что активность компонента в растворах, близких к совершенным, всегда меньше единицы, и только для компонента, находящегося в чистом состоянии, a_i = 1. Из уравнения (VI.3) и из закона Рауля (x_i — p_i/p

0

i

) следует, что для совершенного раствора активность равна молярной доле. Если поведение раствора отклоняется от совершенного, то a_i ≠ x_i. Степень этого отклонения определяется величиной коэффициента

В случае совершенных растворов γ_i = 1 и a_i = x_i. Для реальных растворов коэффициент активности может быть как меньше единицы (отрицательные отклонения), так и больше (положительные отклонения). Если для реальных

растворов вместо молярной доли использовать активность, то закон Рауля сохраняет свою форму, т.е. p_i = p

0

a

a_i.

Из сказанного следует, что введение новой функции активности является формальным приемом, упрощающим термодинамические соотношения и позволяющим проводить расчеты равновесий с участием реальных растворов. Понятие активности само по себе не вскрывает механизма межчастичного взаимодействия в растворах, его недостаточно для полного описания системы, которое возможно лишь на основе молекулярно-статистических представлений. Однако измерения активности как для решения конкретных задач, так и для систематизации опытных данных, необходимы для развития теории растворов.

Измерения активности дают возможность оценить отклонения в поведении реальных растворов от идеальных. В современной литературе экспериментальные данные по равновесиям излагаются преимущественно в терминах активности.

В разбавленных растворах, как указывалось ранее, для растворителя выполняется закон Рауля: p₁ — p

0

1

x₁, а для растворенного вещества закон Генри: c_i = p_i/г_i.

В случае растворов, близких к разбавленным, для растворителя в качестве стандартного состояния целесообразно принять этот компонент в чистом состоянии. При этом, как и для растворов, близких к совершенным, закон Рауля для растворителя может быть распространен на концентрированные растворы при условии замены молярной доли активностью, т.е. p₁ = p

0

1

a₁.

Для растворенного вещества выбор стандартного состояния должен быть сделан таким образом, чтобы в растворе любой концентрации соблюдался закон Генри. Сопоставление уравнения р_i = p

ст

i

с уравнением c_i = p_i/г_i показывает, что для этого необходимо, чтобы р

ст

i

= г_i, т.е. давление пара растворенного вещества в стандартном состоянии должно быть численно равно величине коэффициента Генри (г). При этом

В разбавленном растворе a_i = с_i, а при любых более высоких концентрациях закон Генри сохраняется при за мене концентрации активностью. При рассмотрении таких растворов также вводится коэффициент активности, равный отношению a_i/c_i. В отличие от растворов, близких к совершенным, его принято обозначать буквой f_i, т.е. a_i/c_i = f_i.

По одному из определений следует, что активностью называется величина, подстановка которой вместо концентрации в термодинамические уравнения делает последние применимыми для реальных растворов. Оно, однако, справедливо лишь для уравнений, описывающих равновесие, но не для других термодинамических уравнений.

Источник

Стандартные состояния

Станд а ртные состо я ния, условно принятые термодинамические состояния индивидуальных веществ и компонентов растворов. Представление о стандартных состояниях введено в связи с тем, что простые термодинамические закономерности не описывают достаточно точно поведение реальных веществ, когда количественной характеристикой служит давление р или концентрация с. Термодинамические уравнения для идеальных газов и растворов можно применять к реальным системам, если вместо давления р использовать фугитивность f, а вместо концентрации с — активность а. Отсчёт а и f принято начинать для всех веществ в их стандартных состояниях.

Стандартное состояние газа при каждой температуре — это гипотетическое состояние идеального газа, когда f = р = 1 и газ обладает свойствами, присущими реальному газу при бесконечно малом давлении. Для жидких и кристаллических индивидуальных веществ в качестве стандартного состояния при каждой температуре принимается их состояние под нормальным давлением. В случае растворов за стандартное состояние для растворителя обычно принимают состояние чистого растворителя, а для растворённого вещества — его состояние в бесконечно разбавленном растворе, когда для него а = с (обычно с — мольная доля или молярность; см. Концентрация). Изменения термодинамических параметров — гиббсовой энергии, энтропии и др. — для какого-либо процесса, вычисляемые с помощью f или а, не зависят от выбора стандартного состояния при условии, что в данном расчёте оно неизменно для всех начальных и конечных состояний. К символам, обозначающим свойства вещества (характеристики процесса) в стандартном состоянии, добавляется знак градуса как верхний индекс (например, D Н°_обр — стандартная энтальпия образования какого-либо вещества).

Представления о стандартных состояниях широко используются в физической химии. При сравнении термодинамических функций (см. Термодинамика химическая) и проведении термохимических расчётов (например, на основе Гесса закона) необходимо, чтобы все тепловые эффекты реакций были отнесены к одинаковым условиям, т.к. они зависят от температуры (в меньшей степени от давления), а для реакций в растворах — от концентрации. В термохимии в качестве стандартного состояния принимают состояние веществ, в котором они находятся при 298,15 К и р = 1 атм (760 мм рт. ст.). Следует отметить, что возможность существования вещества в стандартном состоянии не обязательна; так, в расчётах может фигурировать теплота образования газообразной H₂O в стандартном состоянии, хотя подобное состояние, для водяного пара при р = 1 атм и 25 °С термодинамически невозможно.

Лит.: Карапетьянц М. Х., Химическая термодинамика, 3 изд., М., 1975.

Источник

Выбор стандартного состояния

Понятие об активности компонента

Рассмотренные выше разбавленные и совершенные растворы относятся к классу идеальных растворов. Уравнения, выведенные для описания этих растворов, не пригодны для термодинамического анализа реальных металлургических систем: сплавов, шлаков, штейнов и др. Особенностью таковых является наличие в них взаимодействия между частицами компонентов раствора. Именно наличие этого взаимодействия обуславливает отклонения в поведении компонентов раствора от поведения компонентов в идеальных растворах. Термодинамические уравнения, выведенные для идеальных растворов, позволяют на основе свойств компонентов предсказывать свойства раствора в целом и наоборот. Поэтому возникла задача найти такую характеристику раствор, которая могла бы связать свойства реальных растворов, и на основании которой можно было хотя бы приближённо предсказывать свойства реального раствора на основе известных свойств компонентов. Из общих соображений эта характеристика должна отвечать следующим требованиям:

— через неё должны легко выражаться термодинамические свойства раствора;

— в предельных случаях, когда реальный раствор становится идеальным, она должна совпадать с концентрацией;

— с помощью этой характеристики желательно сохранить форму уравнений, выражающих законы идеальных растворов.

Всем этим требованиям отвечает термодинамическая активность. Под термодинамической активностью понимают величину, после подстановки которой в уравнения для идеальных растворов вместо концентрации компонента, становится возможным использовать эти уравнения для термодинамического анализа реальных растворов.

Одним из основных термодинамических уравнений теории растворов является уравнение химического потенциала. Это уравнение имеет вид:

— для растворённого вещества разбавленного раствора

μ_i = μ + RTlnC₁; (10.1)

— для растворителя разбавленного раствора

μ₁ = μ + RTlnХ₁; (10.2)

— для любого компонента совершенного раствора

μ_i = μ + RTlnХ₁. (10.3)

С учётом определения термодинамической активности уравнение химического потенциала компонента реального раствора будет иметь вид:

μ_i = μ +RTln , (10.4)

где μ_i – химический потенциал i – го компонента реального раствора;

μ — стандартный потенциал i – го компонента реального раствора;

-термодинамическая активность i –го компонента реального раствора.

Из уравнения (10.1) видно, что если = 1, то μ_i = μ . Таким образом, в стандартном состоянии активность компонента реального раствора равна единице. Очевидно, что для компонентов идеальных растворов μ = μ .

Термодинамическая активность является безразмерной величиной и определяется давлением насыщенного пара компонента. Рассмотрим равновесие раствор – пар. Для условий равновесия справедливо:

μ_i = μ_i(газ) = μ + RTlnP_i (10.5)

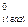
C другой стороны для стандартного состояния, как и для любого, можно записать:

μ = μ + RTlnP (10.6)

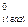
Вычитая из уравнения (10.5) уравнение (10.6), получим:

μ_i = μ + RTln (10.7)

Сравнение (10.7) и (10.4) даёт:

(10.8)

Таким образом, термодинамическая активность определяется как отношение давления пара компонента над реальным растворов к давлению пара этого компонента в стандартном состоянии.

Выбор стандартного состояния

Для расчёта активности компонента реального раствора помимо давления пара компонента над реальным раствором необходимо знать стандартное состояние этого компонента для определения давления его паров в этом состоянии. Обычно в качестве стандартного выбирается такое состояние компонента, при котором поведение реального раствора становится таким же, как и идеального. В таком состоянии активность компонента совпадает с его концентрацией.

Выберем стандартное состояние для компонентов реального раствора, близкого к совершенному раствору. Для любого компонента совершенного раствора справедлив закон Рауля:

Х_i = (10.9)

Для активности компонента реального раствора можно записать:

= (10.2)

Для стандартного состояния компонента реального раствора справедливо:

или = (10.3)

откуда видно, что

P = P (10.4)

Поскольку P представляет собой давление пара компонента над чистым жидким компонентом, то в качестве стандартного состояния для любого компонента реального раствора близкого к совершенному раствору принимается чистый компонент. Тогда активность компонента такого раствора будет выражаться уравнением:

, (10.5)

а закон Рауля для каждого компонента раствора уравнением:

P_i = _iP , (10.6)

где — активность i – го компонента раствора;

P_i – давление пара i – го компонента над реальным раствором;

P — давление пара i – го компонента над чистым жидким компонентом.

Рассуждая аналогичным образом, можно показать, что в качестве стандартного состояния для растворителя в реальном разбавленном растворе принимается чистый жидкий растворитель. Для него также справедливы уравнения (10.5) и (10.6).

Рассмотрим стандартное состояние для растворённого вещества реального разбавленного раствора. Для растворенного вещества идеального разбавленного раствора справедлив закон Генри:

Активность растворённого вещества в разбавленном растворе определяется уравнением:

= (10.8)

Для стандартного состояния растворённого вещества реального разбавленного раствора справедливо:

или Г_iР_i = (10.9)

Из сравнения видно, что

Р = (10.10)

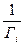
Уравнение (10.10) отвечает такому состоянию реального раствора при котором начинает соблюдаться закон Генри. Тогда закон Генри для растворенного вещества будет иметь вид:

= Г_iP_i (10.11)

Количественной мерой отклонения в поведении компонентов реального раствора от поведения компонентов в идеальных растворах служит коэффициент активности компонента. Для растворителя в реальном разбавленном растворе и любого компонента реального раствора , близкого к совершенному раствору, коэффициент активности выражается уравнением:

γ_i = , (10.12)

а для растворённого вещества реального разбавленного раствора уравнением:

γ_i = , (10.13)

где γ_i – коэффициент активности i – го компонента раствора.

Если γ_i > 1, то говорят о положительном отклонении в поведении компонента от законов идеальных растворов. Если γ_i

Источник