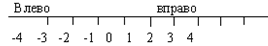Способы введения отрицательных чисел индуктивный

Методика введения понятия отрицательного числа

1. Вопросы, связанные с отрицательными числами являются одним из трудных вопросов для освоения учащимися.

История развития математики показывает, что отрицательные числа значительно труднее дались человеку, это связано с тем, отрицательные числа менее связаны с практической жизнью.

Отрицательные числа возникли в связи с необходимостью выполнения с известными числами. Математики древней Греции не признали отрицательных чисел, они не могли дать им конкретного толкования. Лишь работу Диофанта (3 в. н.э) встречаются преобразования, которые приводят к необходимости выполнения операций над отрицательными числами.

Отрицательные числа появляются лишь в зачаточной форме. Довольно широкое распределение они получили в работах индийских ученых. Положительные числа они называли настоящими, а отрицательные- не настоящими- ложными. Отрицательные числа рассматривали, как долг, а положительные числа как наличные деньги.

Первые правила сложения и вычитания принадлежат индийским ученым. И связаны с трактовкой этих чисел как имущество и долг.

Ученые долго не могли объяснить, дать трактовку произведения двух отрицательных чисел. Почему произведение 2-х долгов есть имущество. Такие ученые как Эйлер, Коми давали свое объяснение правилу произведения чисел, но они приводили к ошибочным результатам.

Немецкий ученый М. Штифель впервые в 1544 г. дал определение отрицательных чисел, как чисел меньших нуля.

Впервые математическую интерпретацию дал Рене Декарт в 1737 г. в книги «Аналитическая геометрия». Отрицательные числа он рассматривал как самостоятельное, расположенное на оси ОХ влево от начало координат. Однако он эти числа назвал ложными. Всеобщее признание отрицательные числа получили в первой половине 21 века, так отрицательные числа вошли в историю математики.

2. Различные приемы введения отрицательных чисел. В учебной литературе можно отметить 3 способа введения отрицательных чисел.

1) Рассматриваются случаи, когда вычисление на множестве положительных чисел ложно.

2) Рассматривают векторы расположенные на одной прямой, необходимость охарактеризовать не только их длину, но и направление приводит к понятию положительных и отрицательных чисел.

3) Введение отрицательных чисел посредством расположения изменяющихся величин в противоположных направлениях.

Методика введения отрицательного числа.

Прежде чем дать понятие об отрицательном числе необходимо показать на конкретных примерах, что известно уч-ся чисел недостаточно для характеристики положения точки на прямой к началу отсчета.

На достаточном количестве примеров надо показать неудобства понятия типа вправо или влево, вверх или вниз начертить числовую ось. Необходимо отложить начало отсчета и чтоб для определенности таких шкал, которые находятся вправо со знаком плюс, влево с противоположным знаком- минус.

В учебнике рассматривается достаточное число примеров, показывающих о целесообразности использования определенных знаков для обозначения направления противоположности движения. Для понятия введения отрицательного числа необходимо пользоваться демонстративным термометром и другими пособиями.

Знакомству с противоположными числами способствует изучение центра симметрии.

Понятие о противоположных числах связывается симметричными точками. В тоже время введение этого понятия основывается с геометрическим истолкованием положительных и отрицательных чисел.

В пункте противоположных чисел вводится определение целых чисел. Натуральные числа, противоположные числа, нуль- называют целыми числами. Модуль числа- понятие модуль числа дает от начала отсчета до точки соответствующему числу. Следует обратить внимание учащихся как мотивировать определение модуля числа.

В учебниках понятие модуля числа вводится путем рассмотрения примеров, поясняют как находить модуль числа. Поясняется, что модуль числа не может быть отрицательным ибо модуль числа это расстояние- обращается внимание, что для положительного числа модуль равен самому числу. Модуль отрицательного числа равен противоположному числу.

Соотношения равенства и неравенства между положительными и отрицательными числами вводится по определению, они не могут быть получены путем доказательства, причем очень важно показать учащимся целесообразность определения на конкретных примерах и геометрических образах.

Учащиеся должны на столько прочно усвоить расположение чисел на числовой прямой, чтобы это могло служить основным средством сравнения чисел. Иногда возникают трудности в сравнении отрицательных чисел, чтобы преодолеть их, необходимо рассмотреть их на числовой прямой.

Действия над отрицательными и положительными числами.

Основное, что надо учитывать учителю при рассмотрении этого материала – это действия сложения и вычитания над положительными и отрицательными числами вводится по определению, причем формулировки этих определений должны включать в себя ранее известные учащимся понятия об этих действиях. Вычитание и деление определяются как обратные сложению и умножению.

В учебнике отдельно дается определение действия сложения чисел с разными знаками, формулировки этих правил содержат указание на следующие действия. В учебнике большое время уделяется к тому как подойти к действию сложению. Основное внимание уделяется к рассмотрению конкретных задач, обращаясь при этом к координатной прямой.

Каким бы путем не вводилось правило сложение учащимся должно быть ясно, что ничто не доказывается при рассмотрении следующих примеров.

Примеры признаны лишь иллюстрировать целесообразность правил. Учащиеся должны овладеть навыками выполнения сложения 2-х отрицательных чисел с разными знаками, противоположных чисел, нуля с положительными и отрицательными числами.

Рассматривая свойства действий важно показать учащимся, что при установленных определениях действий сложения и вычитания чисел сохраняется все те законы которые имели место для положительных чисел.

Учащимся дается формулировка переместительного и сочетательного законов запись каждого из них с помощью букв.

Вычитание отрицательных чисел определяются как действие обратное сложению. Вычитание сводится к прибавлению противоположного числа.

Умножение положительных и отрицательных чисел представляет наибольшую трудность, трудность заключается в том, что учащейся испытывают потребность в доказательстве правил знаков при умножение, а учитель должен убедить учащихся, что такого доказательства нельзя искать или требовать, таким образом действие умножения вводится по определению, которое можно ввести по разному и по разному истолковать правило знаков. Сложения и умножения имеют много общего, однако трактовка правил умножения вызывает больше трудности.

Рассмотрим объяснения правил умножения является рассмотрение конкретных задач, решение которых требует вычисление по формуле а в, при различных а и в. недостатком этого метода является, то что они доказывают правило умножения.

Многие авторы придерживаются пути, когда в начале дается формулировка правил умножения, затем оно поясняется на примерах, задачах. Учащийся убеждаются на конкретном математическом в практичной целесообразности введенного определения. обычно в учебниках формулировки правил умножения чисел с разными знаками и правил умножения натуральных чисел представляет расписания рядов примеров.

При этом используется положение о том, что если изменить знак одного из множителей, то изменится знак произведения.

Правило формулируется удобным для использования вида. Необходимо обратить внимание учащихся на условия равенство произведения нулю.

Деление положительных, отрицательных чисел рассматривается как действие обратное умножению. Учащемуся сообщается, что деление положительных и отрицательных чисел имеет тот же смысл, что и деление положительных чисел. Важно обратить внимание на законы вычисления и умножения выражений.

Так же как и в случая сложения, правило сложения и умножения натуральных чисел может быть выведены из умножения чисел. Считая, что правило знаков для суммы известно.

В 6 классе в теме рациональные числа вводятся памяти отрицательные числа, которое может быть записано в виде дроби. Расписывается множество рациональных чисел можно сбить внимание, что когда выполнимо :, +, *, — на число не равное нулю.

При вычитании или выполни действий учащийся получают числа того же множества и это множество обладает свойством замкнутости по отношению к действиям первой и второй степени. Для сложения справедливы переместительный и сочетательный законы имеется нейтральный элемент, имеется противоположный элемент.

Для умножения справедливы первый распределительный и сочетательный закон, имеется нейтральный элемент 1, противоположный элемент ( ).

Практическое занятие №2

Тема: Изучение функции в ШКМ

Содержание практического занятия:

1. Методика введения понятия функции.

2. Методика изучения отдельных функций

3. Виды функций, изучаемых в основной школе

Литература: 3,[7], 16, [18]. Дополнительная литература I.2

Источник

27. Методика введения отрицательных чисел.

Первая методическая задача, возникающая при введении отрицательных чисел, состоит в том, чтобы убедить учащихся в необходимости введения новых чисел. Достигается это с помощью целесообразно подобранных задач. Например: Белка вылезла из дупла и бегает по стволу дерева вверх и вниз. Покажите на рисунке: 1) где будет находиться белка, если она удалена от дупла 3 м ; 2) где окажется белка, если она будет: а) выше дупла на 2 б) ниже дупла на З м; в) ниже дупла на 1,5 м; г) выше дупла 2,5 м. При решении этих задач устанавливается, что для того, чтобы определить местоположение белки на дереве, необходимо знать: расстояние, на которое она удалена дупла, и направление, в котором она переместилась (выше дупла, ниже дупла). Выясняется, что известных чисел недостаточно для того, чтобы охарактеризовать ими и расстояние, и направление. Необходимы новые числа. Рассмотренные выше задачи полезно представить более математизированной форме. для этого достаточно вместо дерева взять прямую, вместо дупла — некоторую фиксированную точку этой прямой, вместо белки произвольную точку прямой. Созданию наглядно-геометрической основы для введения новых чисел служит такая задача. Проведите прямую слева направо и отметьте на ней точку Изобразите на этой прямой точки А, В, С и К, если известно, точка А расположена правее О на б клеток, точка В — правее О 5,5 клетки, точка С — левее О на 2 клетки и точка К — левее О 7,5 клетки. В результате учащиеся будут подготовлены к восприятию понятия «координатная прямая». Учителю останется лишь ввести термины: «начало отсчета», положительное направление прямой, отрицательное направление прямой». Если положительное направление обозначать знаком + отрицательное — знаком -, то ясно, что положение точки А в предыдущей задаче определяется числом +6, положение точки В — числом +5,5, положение точки С — числом -2, положение точки К — числом -7,5, положение самой точки О — числом О. Числа +6, +5,5, 0 были известны ранее, числа —2, —7,5 — новые. Числа +6, +5,5, . называются положительными (их можно записывать и без знака ‘+), числа —2,—7,5. — отрицательными. С помощью положительных, отрицательных чисел и числа О можно полностью охарактеризовать положение точки на прямой. Важно, чтобы учащиеся осознали не только необходимость введения новых чисел, но и правильно понимали их смысл. В этих целях полезны упражнения на чтение и запись положительных и отрицательных чисел, на изображение их. точками на координатной прямой. Вот одно из них. Приведенные ниже предложения запишите короче, используя знаки +» и —»: 1) Температура воздуха в полночь была 4 градуса ниже нуля, а в полдень 10 градусов выше нуля; 2) уровень воды в порту во время прилива был на 1,9 м выше нулевой отметки, а во время отлива — на 1,9 м ниже нулевой отметки; 3) стрелка прибора отклонилась от нулевой отметки на 4,5 деления вправо; на 2,5 деления влево. Полезны задания и на обратный перевод (с математического языка на естественный): Посмотрим, как вводятся действия над положительными и отрицательными числами. Правила выполнения действий над положительными и отрицательными числами устанавливаются на основании решения содержательных задач (например, задач на определение температуры). Математические формулировки этих правил опираются на понятие модуля числа. Приведем методическую схему введения правила сложения положительных и отрицательных чисел (в основу ее положено индуктивное обобщение): 1) показать, что результат изменения температуры находится с помощью действия сложения; 2) па основании измерений температуры с помощью термометра выполнить следующие действия: +2++(+3)=+5, —2+(-3)=—5, —2+(+3)=+1, +2+(—3) =—1; З) ввести установку: каждое число определяется своим модулем и знаком; с помощью этой установки высказать догадки о том, как найти модуль суммы и ее знак (соответствующие записи полезно оформить в виде таблицы): +2+(+3)=+(+│2│+│+3│)=+5,—2+(—3)=—(‚ │—2│+│—3│)=-5, —2+(+З)= +(│+3│—│—2│)= + 1, +2+(—3)= —(│-3│—│—2│)=-1; 4) сформулировать правило сложения чисел с одинаковыми и разными знаками; 5) закрепить это правило письменными упражнениями с подробными записями, приведенными в п. 3; 6) осуществить переход к более сокращенным записям вычислений, сопроводив их полным устным комментарием; 7) на следующем уроке (в качестве повторения и закрепления правила) привести схему соответствующего алгоритма.

28. Методика изучения действий с целыми числами.

Сравнение ЦЧ: расстояние на координатной прямой от начала отсчета до точки, которая соответствует данному числу наз модулем этого числа или абсолютной увеличенной. Противоположные числа имеют равные модули и разные знаки. Модуль числа 0 равен 0. модуль не равного 0 числа яв-ся числом положительным, т.к. расстояние не может быть отрицательно. Модуль положительного числа равен самому числу, модуль отрицательного числа равен противоположному числу. Для 2 целых чисел больше то которое на координатной прямой расположено правее и меньше то которое расположено левее.

Следовательно для сравнения ЦЧ можно использовать следующие св-ва:

— любое отрицательное число 0

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Оставленные комментарии видны всем.

Для продолжения скачивания необходимо пройти капчу:

Источник

Формирование математических понятий в школьном курсе математики
статья по теме

Формирование у учащихся математических понятий – одна из важнейших задач преподавания математики. Овладение основами наук немыслимо без овладения системой понятий этих наук. В большей мере это относится к математике. Вся постановка преподавания должна способствовать образованию правильных понятий.

Скачать:

Вложение	Размер
формирование математических понятий	58.89 КБ

Предварительный просмотр:

ФОРМИРОВАНИЕ МАТЕМАТИЧЕСКИХ ПОНЯТИЙ В ШКОЛЬНОМ КУРСЕ МАТЕМАТИКИ

Токарева Инна Александровна

МБОУ гимназия №1, Г. Липецк

«Формирование у учащихся математических понятий – одна из важнейших задач преподавания математики. Овладение основами наук немыслимо без овладения системой понятий этих наук. В большей мере это относится к математике. Вся постановка преподавания должна способствовать образованию правильных понятий». [1]

Мышление есть активный процесс отражения объективного мира в сознании человека. Всякое явление, любой процесс представляет собой единство содержания и формы. Структуру отдельных мыслей и их особых сочетаний называют формами мышления . Основными формами мышления являются понятия, суждения, умозаключения. Понятия являются одной из главных составляющих содержания любого предмета, в том числе и предметов математического цикла. Полноценное изучение математических понятий систематизирует знания учащихся, способствует более глубокому освоению предмета. Первостепенная задача учителя математики при изучении любой темы – формирование понятийного аппарата темы.

Понятие — форма мышления, в которой отражены существенные (отличительные) свойства объектов изучения. Понятие считается правильным, если оно верно отражает реально существующие объекты.

Каждое понятие может быть рассмотрено по содержанию и объему. Содержание понятия раскрывается с помощью определения, объем — с помощью классификации. Посредством определения и классификации отдельные понятия организуются в систему взаимосвязанных понятий.

Содержание понятия — это множество всех существенных признаков данного понятия.

Объем понятия — множество объектов, к которым применимо данное понятие.

Например, понятие «треугольник» соединяет в себе класс всевозможных треугольников (объем этого понятия) и характеристическое свойство — наличие трех сторон, трех вершин, трех углов (содержание понятия).

Роль понятий при изучении математики сложна и многообразна. С одной стороны, на понятия мы опираемся в процессе доказательства, с другой – во всяком доказательстве мы раскрываем понятия, углубляем и уточняем знания о понятиях. Само определение понятий также основывается на уже известных понятиях. Поэтому столь важна формулировка определения понятия, которая может быть дана различными способами. Отсюда следует, что одна из основных целей методики преподавания математике – выявить наиболее рациональные способы, с помощью которых можно дать определение того или иного понятия. От этого зависит, насколько хорошо у учащихся сформируется представление о новом понятии.

Методика сообщения определений учащимся обладает известными особенностями, которые объясняются спецификой самих математических предложений, называемых определениями. Выделяют два пути введения определения математических понятий: абстрактно-дедуктивный и конкретно-индуктивный.

Введение понятий абстрактно-дедуктивным методом. При введении понятий органически связанных с уже известными учащимся понятиями можно применить абстрактно-дедуктивный метод. Особенность этого метода состоит в том, что каждое определение вводится сразу, в готовом виде, без предварительного разъяснения на конкретных примерах и образцах. Так, например, понятие квадратного уравнения можно ввести следующим образом:

1. Дать определение нового понятия (уравнение вида аx 2 –bx+c =0, где а≠ 0 называется квадратным), мотивируя обозначающий его термин (наибольший показатель степени неизвестного равен двум; уравнение содержит квадрат неизвестного).
2. Рассмотреть частные (и особые) случаи выражения этого понятия ( x 2 +px+q =0, ax 2 +c =0, ax 2 +bx =0, ax 2 =0), проведя своеобразную классификацию этого понятия. В данном случае классификация может быть такой:

Привести некоторые контр примеры этого понятия (спросить, например, учащихся, будет ли уравнение вида bx+с= 0 неполным квадратным уравнением).

1. Иллюстрировать введенное понятие конкретными примерами ( x 2 –7x+12 =0, 2 x 2 – 32 =0 и т.д.), всякий раз проверяя, удовлетворяет ли каждое из конкретных проявлений этого понятия его определению.
2. Привести конкретные примеры приложения этого понятия (например, известную формулу можно рассмотреть как квадратное уравнение ; использовать квадратное уравнение при решении текстовых задач).

Введение понятий конкретно-индуктивным методом. Сущность конкретно-индуктивного метода заключается в том, что на основе рассмотрения частных примеров учащиеся подготавливаются к самостоятельному формулированию определения.

Например, ознакомление учащихся с простыми и составным числами можно провести следующим способом:

1. На доске написать такие два ряда чисел:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, …

4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, …

1. Выявление и отбор существенных признаков данных понятий. Например, учитель может дать учащимся такое задание: найти все делители каждого из чисел, содержащихся в первом ряду, и найти все делители каждого из чисел, содержащихся во втором ряду.
2. Формулировка определения этих понятий; первичное определение, внесение поправок, вторичное определение (учащиеся).
3. Четкое определение (учитель); повторение определения (учащиеся).

Таким образом, пользуясь конкретно-индуктивным методом, учитель дает учащимся такие конкретные примеры, в которых на первый план выступают существенные признаки данного понятия, и привлекает учащихся к этим признакам.

Конкретно-индуктивный метод находит большое применение в младших классах; в старших классах чаще применяют абстрактно-дедуктивный метод.

Кроме данных двух методов введения математических понятий существует еще один: Учащиеся готовятся к сознательному восприятию, к пониманию нового определения, формулировка которого им сообщается затем в готовом виде. При осуществлении данного метода и конкретно-индуктивного используется эвристический метод, в классе создается проблемная ситуация, которая способствует самостоятельному «открытию» учащимися новых знаний.

В одних случаях можно составить такие упражнения, чтобы на их основе учащиеся легко и быстро сформулировали определение нового понятия. В других случаях этого добиваться не стоит, достаточно ограничиться подготовкой к восприятию нового определения. Например, приступая к изучению геометрической прогрессии, учитель предлагает следующие упражнения.

Выпишите несколько первых членов последовательности ( х n ) , у которой х 1 = 2, х n+1 =x n ∙ 3. Такая последовательность называется геометрической прогрессией. Попытайтесь сформулировать определение геометрической прогрессии.

Упражнение учащиеся выполняют свободно, опираясь на аналогию с уже известным им определением арифметической прогрессии. Когда же вводится понятие арифметической прогрессии, то путем дополнительных вопросов также можно добиться самостоятельного формулирования учащимися определения. Но здесь на аналогию они не опираются, так как с подобным определение встречаются впервые. Поэтому с целью экономии учебного времени лучше изменить упражнение, исключив из него требование о самостоятельном формулировании определения, например:

Выпишите несколько последовательных членом последовательности ( х n ), у которой х 1 = 4, х n+1 =x n + 3. Далее учитель говорит, что такая последовательность называется арифметической прогрессией, и сам сообщает ее определение.

Таким образом, метод ознакомления учащихся с новым определением выбираю в зависимости от характера изучаемого материала, наличие учебного времени, уровня развития учащихся и других факторов.

Учитывая, что упражнения являются основным средством формирования понятий в средней школе, сопоставим в виде схемы каждый этап формирования понятия и соответствующие ему виды упражнений:

Этапы формирования понятия

Упражнения, реализующие их

Мотивация введения понятия

Упражнения на применение изученных понятий и теорем.

Упражнения практического характера.

Выделение существенных свойств понятия

Упражнение на построение объектов, удовлетворяющих указанным свойствам.

Усвоение логической структуры определения понятия

Упражнения с моделями фигур.

Упражнения на распознавание объектов, принадлежащих объему понятия.

Упражнения на выделение следствий из определения понятия.

Упражнения на дополнение условий (распознавание и выведение следствий).

Упражнения на составление родословной понятия.

Установление связей изучаемого понятия с другими понятиями

Упражнения на применение понятия в различных ситуациях.

Упражнения на систематизацию понятий.

Итак, формирование понятия осуществляется в несколько этапов:

1. мотивация (подчеркивается важность изучения понятия, активизируется целенаправленная деятельность школьников, возбуждается интерес к изучению понятия с помощью привлечения средств нематематического содержания, выполнения специальных упражнений, объясняющих необходимость развития математической теории);

2. выявление существенных свойств понятия (выполнение упражнений, где выделяются существенные свойства изучаемого понятия);

3. формулировка определения понятия (выполнение действий на распознавание объектов, принадлежащих понятию, конструирование объектов, относящихся к объему понятия).

1. Никитин В.В., Рупасов К.А. Определения математических понятий в курсе средней школы: Пособие для учителей. – М.: УЧПЕДГИЗ, 1963.
2. Груденов Я.И. Изучение определений, аксиом, теорем: Пособие для учителей. – М.: Просвещение, 1981.
3. Саранцев Г.И. Формирование математических понятий в средней школе.//Математика в школе. 1998 — №6 – с.27.

Источник