Способы введения математических понятий

Формирование математических понятий в школьном курсе математики
статья по теме

Формирование у учащихся математических понятий – одна из важнейших задач преподавания математики. Овладение основами наук немыслимо без овладения системой понятий этих наук. В большей мере это относится к математике. Вся постановка преподавания должна способствовать образованию правильных понятий.

Скачать:

Вложение	Размер
формирование математических понятий	58.89 КБ

Предварительный просмотр:

ФОРМИРОВАНИЕ МАТЕМАТИЧЕСКИХ ПОНЯТИЙ В ШКОЛЬНОМ КУРСЕ МАТЕМАТИКИ

Токарева Инна Александровна

МБОУ гимназия №1, Г. Липецк

«Формирование у учащихся математических понятий – одна из важнейших задач преподавания математики. Овладение основами наук немыслимо без овладения системой понятий этих наук. В большей мере это относится к математике. Вся постановка преподавания должна способствовать образованию правильных понятий». [1]

Мышление есть активный процесс отражения объективного мира в сознании человека. Всякое явление, любой процесс представляет собой единство содержания и формы. Структуру отдельных мыслей и их особых сочетаний называют формами мышления . Основными формами мышления являются понятия, суждения, умозаключения. Понятия являются одной из главных составляющих содержания любого предмета, в том числе и предметов математического цикла. Полноценное изучение математических понятий систематизирует знания учащихся, способствует более глубокому освоению предмета. Первостепенная задача учителя математики при изучении любой темы – формирование понятийного аппарата темы.

Понятие — форма мышления, в которой отражены существенные (отличительные) свойства объектов изучения. Понятие считается правильным, если оно верно отражает реально существующие объекты.

Каждое понятие может быть рассмотрено по содержанию и объему. Содержание понятия раскрывается с помощью определения, объем — с помощью классификации. Посредством определения и классификации отдельные понятия организуются в систему взаимосвязанных понятий.

Содержание понятия — это множество всех существенных признаков данного понятия.

Объем понятия — множество объектов, к которым применимо данное понятие.

Например, понятие «треугольник» соединяет в себе класс всевозможных треугольников (объем этого понятия) и характеристическое свойство — наличие трех сторон, трех вершин, трех углов (содержание понятия).

Роль понятий при изучении математики сложна и многообразна. С одной стороны, на понятия мы опираемся в процессе доказательства, с другой – во всяком доказательстве мы раскрываем понятия, углубляем и уточняем знания о понятиях. Само определение понятий также основывается на уже известных понятиях. Поэтому столь важна формулировка определения понятия, которая может быть дана различными способами. Отсюда следует, что одна из основных целей методики преподавания математике – выявить наиболее рациональные способы, с помощью которых можно дать определение того или иного понятия. От этого зависит, насколько хорошо у учащихся сформируется представление о новом понятии.

Методика сообщения определений учащимся обладает известными особенностями, которые объясняются спецификой самих математических предложений, называемых определениями. Выделяют два пути введения определения математических понятий: абстрактно-дедуктивный и конкретно-индуктивный.

Введение понятий абстрактно-дедуктивным методом. При введении понятий органически связанных с уже известными учащимся понятиями можно применить абстрактно-дедуктивный метод. Особенность этого метода состоит в том, что каждое определение вводится сразу, в готовом виде, без предварительного разъяснения на конкретных примерах и образцах. Так, например, понятие квадратного уравнения можно ввести следующим образом:

1. Дать определение нового понятия (уравнение вида аx 2 –bx+c =0, где а≠ 0 называется квадратным), мотивируя обозначающий его термин (наибольший показатель степени неизвестного равен двум; уравнение содержит квадрат неизвестного).
2. Рассмотреть частные (и особые) случаи выражения этого понятия ( x 2 +px+q =0, ax 2 +c =0, ax 2 +bx =0, ax 2 =0), проведя своеобразную классификацию этого понятия. В данном случае классификация может быть такой:

Привести некоторые контр примеры этого понятия (спросить, например, учащихся, будет ли уравнение вида bx+с= 0 неполным квадратным уравнением).

1. Иллюстрировать введенное понятие конкретными примерами ( x 2 –7x+12 =0, 2 x 2 – 32 =0 и т.д.), всякий раз проверяя, удовлетворяет ли каждое из конкретных проявлений этого понятия его определению.
2. Привести конкретные примеры приложения этого понятия (например, известную формулу можно рассмотреть как квадратное уравнение ; использовать квадратное уравнение при решении текстовых задач).

Введение понятий конкретно-индуктивным методом. Сущность конкретно-индуктивного метода заключается в том, что на основе рассмотрения частных примеров учащиеся подготавливаются к самостоятельному формулированию определения.

Например, ознакомление учащихся с простыми и составным числами можно провести следующим способом:

1. На доске написать такие два ряда чисел:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, …

4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, …

1. Выявление и отбор существенных признаков данных понятий. Например, учитель может дать учащимся такое задание: найти все делители каждого из чисел, содержащихся в первом ряду, и найти все делители каждого из чисел, содержащихся во втором ряду.
2. Формулировка определения этих понятий; первичное определение, внесение поправок, вторичное определение (учащиеся).
3. Четкое определение (учитель); повторение определения (учащиеся).

Таким образом, пользуясь конкретно-индуктивным методом, учитель дает учащимся такие конкретные примеры, в которых на первый план выступают существенные признаки данного понятия, и привлекает учащихся к этим признакам.

Конкретно-индуктивный метод находит большое применение в младших классах; в старших классах чаще применяют абстрактно-дедуктивный метод.

Кроме данных двух методов введения математических понятий существует еще один: Учащиеся готовятся к сознательному восприятию, к пониманию нового определения, формулировка которого им сообщается затем в готовом виде. При осуществлении данного метода и конкретно-индуктивного используется эвристический метод, в классе создается проблемная ситуация, которая способствует самостоятельному «открытию» учащимися новых знаний.

В одних случаях можно составить такие упражнения, чтобы на их основе учащиеся легко и быстро сформулировали определение нового понятия. В других случаях этого добиваться не стоит, достаточно ограничиться подготовкой к восприятию нового определения. Например, приступая к изучению геометрической прогрессии, учитель предлагает следующие упражнения.

Выпишите несколько первых членов последовательности ( х n ) , у которой х 1 = 2, х n+1 =x n ∙ 3. Такая последовательность называется геометрической прогрессией. Попытайтесь сформулировать определение геометрической прогрессии.

Упражнение учащиеся выполняют свободно, опираясь на аналогию с уже известным им определением арифметической прогрессии. Когда же вводится понятие арифметической прогрессии, то путем дополнительных вопросов также можно добиться самостоятельного формулирования учащимися определения. Но здесь на аналогию они не опираются, так как с подобным определение встречаются впервые. Поэтому с целью экономии учебного времени лучше изменить упражнение, исключив из него требование о самостоятельном формулировании определения, например:

Выпишите несколько последовательных членом последовательности ( х n ), у которой х 1 = 4, х n+1 =x n + 3. Далее учитель говорит, что такая последовательность называется арифметической прогрессией, и сам сообщает ее определение.

Таким образом, метод ознакомления учащихся с новым определением выбираю в зависимости от характера изучаемого материала, наличие учебного времени, уровня развития учащихся и других факторов.

Учитывая, что упражнения являются основным средством формирования понятий в средней школе, сопоставим в виде схемы каждый этап формирования понятия и соответствующие ему виды упражнений:

Этапы формирования понятия

Упражнения, реализующие их

Мотивация введения понятия

Упражнения на применение изученных понятий и теорем.

Упражнения практического характера.

Выделение существенных свойств понятия

Упражнение на построение объектов, удовлетворяющих указанным свойствам.

Усвоение логической структуры определения понятия

Упражнения с моделями фигур.

Упражнения на распознавание объектов, принадлежащих объему понятия.

Упражнения на выделение следствий из определения понятия.

Упражнения на дополнение условий (распознавание и выведение следствий).

Упражнения на составление родословной понятия.

Установление связей изучаемого понятия с другими понятиями

Упражнения на применение понятия в различных ситуациях.

Упражнения на систематизацию понятий.

Итак, формирование понятия осуществляется в несколько этапов:

1. мотивация (подчеркивается важность изучения понятия, активизируется целенаправленная деятельность школьников, возбуждается интерес к изучению понятия с помощью привлечения средств нематематического содержания, выполнения специальных упражнений, объясняющих необходимость развития математической теории);

2. выявление существенных свойств понятия (выполнение упражнений, где выделяются существенные свойства изучаемого понятия);

3. формулировка определения понятия (выполнение действий на распознавание объектов, принадлежащих понятию, конструирование объектов, относящихся к объему понятия).

1. Никитин В.В., Рупасов К.А. Определения математических понятий в курсе средней школы: Пособие для учителей. – М.: УЧПЕДГИЗ, 1963.
2. Груденов Я.И. Изучение определений, аксиом, теорем: Пособие для учителей. – М.: Просвещение, 1981.
3. Саранцев Г.И. Формирование математических понятий в средней школе.//Математика в школе. 1998 — №6 – с.27.

Источник

Методы и приемы введения математических понятий в начальном курсе математики

Дата публикации: 13.07.2020 2020-07-13

Статья просмотрена: 698 раз

Библиографическое описание:

Склянная, Т. Н. Методы и приемы введения математических понятий в начальном курсе математики / Т. Н. Склянная. — Текст : непосредственный // Молодой ученый. — 2020. — № 28 (318). — С. 104-107. — URL: https://moluch.ru/archive/318/72610/ (дата обращения: 18.11.2021).

В статье автор анализирует виды определения математических понятий, методы и приемы их осознанного усвоения младшими школьниками (на примере УМК «Школа России»).

Ключевые слова: понятие, явные определения, неявные определения, младший школьник, начальный курс математики, ломаная линия, математическая запись, начальная школа, понятийный аппарат, изучение математики

Общеизвестно, что «первая встреча» с любой наукой начинается со знакомства с ее понятийным аппаратом. Отрасль научного знания может считаться сложившейся, если устоялся её терминологический аппарат, когда входящие в него термины связывают «иерархические отношения» и «взаимообусловленные связи».

С самого рождения ребенок познает мир, узнает предметы / объекты окружающей действительности, где особое место занимает речевое развитие. Вместе с тем, специально организованным и целенаправленным этот процесс становится как правило, на первой школьной ступени образования. С началом школьного обучения ребенок осваивает новый для него языковый стиль — учебно-научный. Признаками его освоения выступает использование в речи достаточно большого количества терминов и слов с абстрактным значением, ее высокая «информационная насыщенность».

«Научить детей пользоваться терминами» — это значит научить их правильно и точно выражать свои мысли в процессе освоения программного материала, что, в свою очередь, выступает показателем освоения школьной дисциплины в целом. Уместность и правильность употребления научных терминов являются показателями усвоения школьниками соответствующих понятий.

«Присвоение» обучающимися категориально-понятийного аппарата любого школьного предмета — процесс длительный, выстраивающийся по определенным этапам. Состоит данный процесс из двух компонентов: введение термина и формулирование его определения. Наибольший интерес, с нашей точки зрения, вызывает исследование данного вопроса при изучении математики.

Начальный курс математики представлен тремя разделами: алгебры и геометрии, которые имеют статус пропедевтических курсов, арифметики — основы математического образования младших школьников. Каждый из разделов представлен определенным понятийным аппаратом: алгебраический — «равенство», «неравенство», «числовое выражение», «переменная» и др.; геометрический — «точка», «прямая», «отрезок», «многоугольник», «геометрическая фигура», «геометрическое тело», «положение на плоскости / в простанстве» и др., арифметический — «число», «цифра», «разрядный состав числа», «арифметическое действие», «сложение», «компоненты и результат действия», «вычислительный прием», «алгоритм выполнения действия», «распределительное свойство умножения, относительно сложения» и др.

Важной составляющей процесса осознанного освоения любой темы является, прежде всего, овладение обучающимися категориально-понятийного аппарата. Следовательно, изучение новой темы начинается с формирования представлений о понятиях, раскрывающих сущность научной информации по данному вопросу.

Понятие, согласно логике — «форма (вид) мысли, или как мысленное образование, есть результат обобщения предметов некоторого вида и мысленное выделение соответствующего класса (множества) по определенной совокупности общих для предметов этого класса — и в совокупности отличительных для них признаков» [1, с.182]; «общее имя, имеющее относительно ясное и устойчивое содержание и сравнительно четко очерченный объем» [2, с. 272].

В начальном курсе математики представлены различные виды определения понятий. Например, построение определения математического понятия через род и видовое отличие — явное определение (прямоугольник — это четырехугольник, у которого все углы прямые»; «цифра — это знак для записи числа» и др.), неявные (остенсивные и контекстуальные) определения (остенсивные: предъявление объекта / понятия: «в математике принято…», «это …»; например: «в математике принято числа при сложении называть слагаемое, слагаемое, сумма (значение суммы)», «это равенство», «это неравенство», «это числовое выражение», «это многоугольник» и др.; контекстуальные: «решить уравнение — значит найти неизвестное число», «луч — часть прямой, ограниченная с одной стороны») и некоторые другие.

Однако по различным программам некоторые понятия определяются по разному. Например, по программе М. И. Моро понятия «равенство» и «неравенство» вводятся остенсивно — предъявляются обучающимся и «получают» название — термин, по программе И. И. Аргинской — «через явное определение»: «Математическая запись, содержащая знак равно, называется равенством», аналогично — неравенство: «Математическая запись, содержащая знаки называется неравенством».

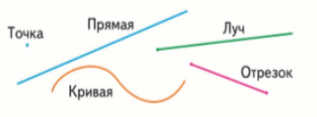
Знакомство с точкой, кривой и прямой линиями — пример остенсивного определения. (М.1. Ч.1. с. 40)

Учащимся предлагается рассмотреть изображенные на странице геометрические фигуры, сообщается название фигур. Затем читается текст на странице учебника.

Примером контекстуального определения является введение понятия «ломаная линия» (М.1, Ч.1 с. 42.). На уроке учащимся предлагается рисунок садового участка, дорожки которого выступают зрительными образами ломаной линии. Дети путем перегибания проволоки по «дорожкам» участка получают модель ломаной линии. Учитель сообщает, что такие линии называются ломаными. Затем открывается учебник и учащиеся читают текст, поясняющий «определяющие особенности» данной линии: «Ломаные линии составлены из отрезков. Эти отрезки — звенья ломаной. У ломаной линии конец одного отрезка — начало другого, кроме концов ломаной. Никакие два соседние звена не лежат на одной прямой. Концы каждого звена — вершины ломаной».

Понятие «задача» также вводится посредством «контекстуального определения». На подготовительном этапе у учащихся на интуитивном уровне формируется представление о том, что задача — это математический рассказ, описывающий реальную жизненную ситуацию, и в котором о чем-то спрашивается. На этапе введения младшим школьникам предлагается текст задачи и сообщается, что такой текст в математике называется задачей. В задаче есть известное — условие и неизвестное — вопрос.

Согласно методике, практически каждое геометрическое понятие на уроках математики в начальной школе вводится наглядно, через наблюдение объекта (объектов) или оперирование им (ими). Например, введение понятия «прямоугольник». Для этого учащимся предлагается проанализировать многоугольники: сравнить, выявить общее и различие.

− Какие фигуры на доске?

− Каким одним словом можно назвать данные фигуры?

− Найдите четырехугольники, у которых все углы прямые.

− Четырехугольники, у которых все углы прямые, называются прямоугольниками.

− Откройте учебник на странице 14 (М.2, Ч.2.). Прочитаем определение в рамочке.

Введение данного понятия — это пример определения понятия «через род и видовой отличие» − явное определение. Такое введение понятия «прямоугольник» раскрывает родственные связи между данным понятием и понятием «четырехугольник». Аналогично вводится понятие «квадрат».

Такая последовательность изучения различных видов многоугольников формирует у младших школьников умение определять место каждого в данном ряду; соотносить новую фигуру с уже знакомой, а значит, осознанно выстраивать определение каждой последующей фигуры; позволяет учащимся выстроить «иерархическую лестницу» между понятиями: многоугольник, четырехугольник, прямоугольник, квадрат.

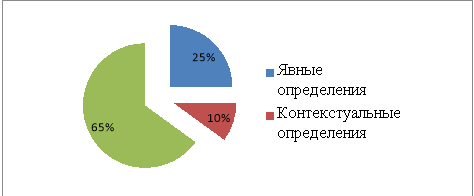
Таким образом, анализ методов и приемов введения понятий начального курса математики позволяет сделать вывод о наличии различных видов определений, где выбор каждого из них во многом определяется сложностью самого математического понятия, психолого-педагогическими и возрастными особенностями ребенка младшего школьного возраста, его готовностью к изучению каждого конкретного понятия. Процентное соотношение явных и неявных определений понятий различно у разных авторов. Так, анализ видов определений геометрических понятий, представленных в программе М.И. Моро, и их соотношение между собой можно отразить в диаграмме (рис.2) .

Рис. 2. Виды геометрических определений

Как показывает педагогическая практика, знания, умения и опыт, которые получают младшие школьники в процессе такой работы, достаточно активно, и, что самое главное, успешно используются в построении рассуждений при определении понятий не только при изучении математики, но и других учебных предметов начальной школы.

1. Войшвилло Е.К Логика: Учеб. для студ. высш. учеб. заведений. / Е. К. Войшвилло, М. Г. Дегтярев — М.: Изд-во ВЛАДОС-ПРЕСС, 2001.
2. Ивин А. А. Словарь по логике / И. И. Ивин, А. Л. Никифоров — М.: Гуманит. изд. центр ВЛАДОС, 1997.
3. Моро М. И. Математика. 1 класс. Учеб. для общеобразоват. Организаций. В 2 ч. Ч.1 / М. И. Моро, С. И. Волкова, С. В. Степанова. М.: Просвещение, 2015.
4. Моро М. И. Математика. 2 класс. Учеб. для общеобразоват. Организаций. В 2 ч. Ч.1 / М. И. Моро, С. И. Волкова, С. В. Степанова. М.: Просвещение, 2015.

Источник