Математические понятия. Методика введения математических понятий и пути их формирования.



Понятие – один из главных составляющих содержания любого предмета, в том числе и предметов математического цикла. Первостепенная задача учителя математики при изучении любой темы формирование понятийного аппарата темы.
Понятие – форма мышления, в которой отражены существенные (отличительные) свойства объектов изучения.
Содержание понятия – это множество всех существенных признаков данного понятия. Раскрывается с помощью определения.
Объем понятия — множество объектов, к которым применимо данное понятие. Раскрывается с помощью классификации. Например: понятие треугольник соединяет в себе класс всевозможных треугольников (объем понятия). Характеристическое свойство – наличие трех сторон, трех вершин, трех углов (содержание понятия).
Характеристические (существенные свойства) – это такие свойства, каждое из которых необходимо, а не вместо достаточного для характеристики объекта принадлежащих понятию.
Понятие: родовое и видовое. Например: Ромб – это параллелограмм, две смежные стороны, которых равны. Родовое понятие – понятие параллелограмма, видовое отличие – две смежные стороны равны.
В отношении объемов различают виды понятий: равнозначимые (совпадают), пересекающиеся, находящие (частично-пересекающиеся) в отношении включения.
Определение понятия – это предложение, в котором раскрываются содержание понятия, т.е. совокупность условий, необходимых и достаточных для выделения класса объектов принадлежащих определяемому понятию.
1.явные – содержат прямое указание на существенные признаки определяемого понятия; определяемое и определяющие в них выражены четко и однозначно. Например: «Прямоугольник есть параллелограмм с прямым углом».
2.неявные – не содержат четкого и однозначного определяющего элемента, в них содержание определяемого может быть установлено через некоторый контекст. Н-р: «Фигура, образованная двумя прямыми, выходящими из одной точки, называются углом».
3.дескрипции – определения мат.объектов путем указания их свойств. Например: «То число, которое будучи умножено на длину диаметра дает длину окружности – дескрипция числа пи».
4.номинальные – с их помощью вводят новый термин символ выражение, как сокращенное для более сложных выражений из ранее введенных терминов или символов, или уточняется значения уже введенного термина символа.
5.реальные – с помошью реальных определений фиксируются характеристические свойства самих определяемых объектов (пятиугольник, есть плоская геометрическая фигура, ограничивающаяся 5-ю сторонами). Одно и то же определение можно представить как номинальное и как реальное (пятиугольником, называется плоская геометрическая фигура, ограниченная 5-ю сторонами).
6.контекстуальные – (часто применяются в начальных классах) – такие определения нового неизвестного термина, понятия, которые выясняются из смысла прочитанного, сводятся к указанию содержащих его контекста.
7.индуктивные – определения, которые позволяют из сходных объектов (теории) путем применения к ним конкретных операций получить новые объекты. Н-р: определение натурального числа.
8.аксиоматические – определения исходных понятий , которые даются посредством исходных понятий некоторой теории через её аксиому. Например: точка, плоскость и расстояние.
9.определение через род и видовые отличия – определения, которые можно рассматривать как частный вид номинальных определений, которые выделяются из предметов ву некоторой области, которые при этом явно упоминаются в определении (род) путем указания характеристического свойства определяемого (видовое отличие).
10.генетические — определения, в которых описываются и указываются способ его происхождения, образования, возникновения и построения. Например: «Шар – это геометрическое тело, образованное вращение полуокружности вокруг диаметра: «Сферой называется поверхность, полученная, вращением полуокружности, вокруг своего диаметра»».
11.определение через абстракцию – определения, связанные с выделением объекта через установление между ними отношений равенства, равнозначности тождества. Например: «Натуральное число n – это характеристика эквивалентных конечных множеств, состоящих из n элементов».

12.остенсивные – определения значений слов путей непосредственного показа, демонстрации предметов.
13.вербальные понятия – это понятия в которых значение неизвестных выражение определяется через выражение с известным значением.
Условие корректности определений: 1.Отсутствие прочного круга и связанного с ним возможности исключения нововведенных терминов. Пример: Решение уравнений – это то число, которое является его решением (такого не должно быть).
2. отсутствие омонимии: каждый термин встречается не более одного раза в качестве определяемого.
Формирование понятия: Формирование понятия – сложный психологический процесс, который осуществляется и протекает по схеме: ощущение -> восприятие-> представление -> понятие.
Этапы формирования понятия:
1. Мотивация (подчеркивается важность изучения понятия, возбуждается интерес к изучению понятия)
2. Выявление существенных свойств понятия (выполнение упражнений, где выделяются существенные свойства изучаемого понятия).
3.Формулировка определений понятия (выполнение действий на распознавание объектов, принадлежащих понятию).
Методы формирования понятия:
1.Конкретно-индуктивный (учитель сам вводит понятие) – в младших классах.
2.Абстрактно- дедуктивный (частично –дедуктивный метод).
Классификация понятий – выявление объема понятий, т.е. разделение множества объектов, составляющих объём родового понятия, на виды. Это разделение основано на сходстве объектов одного вида и отличии их от объектов других видов.
Условия классификации понятий: 1. Классификация проводится по определённому признаку, остающемуся неизменным в процессе классификации.
2. Понятия, получающиеся в результате классификации – взаимно независимые.
3. Сумма объемов понятий, получающихся при классификации, равняется объему исходного понятия.
Пример: Четырехугольник(трапеция и параллелограмм(прямоугольник(квадрат) и ромб(квадрат))) .
Источник
Методы и приемы введения математических понятий в начальном курсе математики
Дата публикации: 13.07.2020 2020-07-13
Статья просмотрена: 698 раз
Библиографическое описание:
Склянная, Т. Н. Методы и приемы введения математических понятий в начальном курсе математики / Т. Н. Склянная. — Текст : непосредственный // Молодой ученый. — 2020. — № 28 (318). — С. 104-107. — URL: https://moluch.ru/archive/318/72610/ (дата обращения: 18.11.2021).
В статье автор анализирует виды определения математических понятий, методы и приемы их осознанного усвоения младшими школьниками (на примере УМК «Школа России»).
Ключевые слова: понятие, явные определения, неявные определения, младший школьник, начальный курс математики, ломаная линия, математическая запись, начальная школа, понятийный аппарат, изучение математики
Общеизвестно, что «первая встреча» с любой наукой начинается со знакомства с ее понятийным аппаратом. Отрасль научного знания может считаться сложившейся, если устоялся её терминологический аппарат, когда входящие в него термины связывают «иерархические отношения» и «взаимообусловленные связи».
С самого рождения ребенок познает мир, узнает предметы / объекты окружающей действительности, где особое место занимает речевое развитие. Вместе с тем, специально организованным и целенаправленным этот процесс становится как правило, на первой школьной ступени образования. С началом школьного обучения ребенок осваивает новый для него языковый стиль — учебно-научный. Признаками его освоения выступает использование в речи достаточно большого количества терминов и слов с абстрактным значением, ее высокая «информационная насыщенность».
«Научить детей пользоваться терминами» — это значит научить их правильно и точно выражать свои мысли в процессе освоения программного материала, что, в свою очередь, выступает показателем освоения школьной дисциплины в целом. Уместность и правильность употребления научных терминов являются показателями усвоения школьниками соответствующих понятий.
«Присвоение» обучающимися категориально-понятийного аппарата любого школьного предмета — процесс длительный, выстраивающийся по определенным этапам. Состоит данный процесс из двух компонентов: введение термина и формулирование его определения. Наибольший интерес, с нашей точки зрения, вызывает исследование данного вопроса при изучении математики.
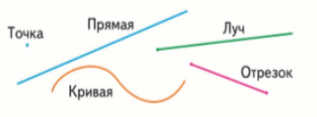
Начальный курс математики представлен тремя разделами: алгебры и геометрии, которые имеют статус пропедевтических курсов, арифметики — основы математического образования младших школьников. Каждый из разделов представлен определенным понятийным аппаратом: алгебраический — «равенство», «неравенство», «числовое выражение», «переменная» и др.; геометрический — «точка», «прямая», «отрезок», «многоугольник», «геометрическая фигура», «геометрическое тело», «положение на плоскости / в простанстве» и др., арифметический — «число», «цифра», «разрядный состав числа», «арифметическое действие», «сложение», «компоненты и результат действия», «вычислительный прием», «алгоритм выполнения действия», «распределительное свойство умножения, относительно сложения» и др.
Важной составляющей процесса осознанного освоения любой темы является, прежде всего, овладение обучающимися категориально-понятийного аппарата. Следовательно, изучение новой темы начинается с формирования представлений о понятиях, раскрывающих сущность научной информации по данному вопросу.
Понятие, согласно логике — «форма (вид) мысли, или как мысленное образование, есть результат обобщения предметов некоторого вида и мысленное выделение соответствующего класса (множества) по определенной совокупности общих для предметов этого класса — и в совокупности отличительных для них признаков» [1, с.182]; «общее имя, имеющее относительно ясное и устойчивое содержание и сравнительно четко очерченный объем» [2, с. 272].
В начальном курсе математики представлены различные виды определения понятий. Например, построение определения математического понятия через род и видовое отличие — явное определение (прямоугольник — это четырехугольник, у которого все углы прямые»; «цифра — это знак для записи числа» и др.), неявные (остенсивные и контекстуальные) определения (остенсивные: предъявление объекта / понятия: «в математике принято…», «это …»; например: «в математике принято числа при сложении называть слагаемое, слагаемое, сумма (значение суммы)», «это равенство», «это неравенство», «это числовое выражение», «это многоугольник» и др.; контекстуальные: «решить уравнение — значит найти неизвестное число», «луч — часть прямой, ограниченная с одной стороны») и некоторые другие.
Однако по различным программам некоторые понятия определяются по разному. Например, по программе М. И. Моро понятия «равенство» и «неравенство» вводятся остенсивно — предъявляются обучающимся и «получают» название — термин, по программе И. И. Аргинской — «через явное определение»: «Математическая запись, содержащая знак равно, называется равенством», аналогично — неравенство: «Математическая запись, содержащая знаки называется неравенством».
Знакомство с точкой, кривой и прямой линиями — пример остенсивного определения. (М.1. Ч.1. с. 40)
Учащимся предлагается рассмотреть изображенные на странице геометрические фигуры, сообщается название фигур. Затем читается текст на странице учебника.
Примером контекстуального определения является введение понятия «ломаная линия» (М.1, Ч.1 с. 42.). На уроке учащимся предлагается рисунок садового участка, дорожки которого выступают зрительными образами ломаной линии. Дети путем перегибания проволоки по «дорожкам» участка получают модель ломаной линии. Учитель сообщает, что такие линии называются ломаными. Затем открывается учебник и учащиеся читают текст, поясняющий «определяющие особенности» данной линии: «Ломаные линии составлены из отрезков. Эти отрезки — звенья ломаной. У ломаной линии конец одного отрезка — начало другого, кроме концов ломаной. Никакие два соседние звена не лежат на одной прямой. Концы каждого звена — вершины ломаной».
Понятие «задача» также вводится посредством «контекстуального определения». На подготовительном этапе у учащихся на интуитивном уровне формируется представление о том, что задача — это математический рассказ, описывающий реальную жизненную ситуацию, и в котором о чем-то спрашивается. На этапе введения младшим школьникам предлагается текст задачи и сообщается, что такой текст в математике называется задачей. В задаче есть известное — условие и неизвестное — вопрос.
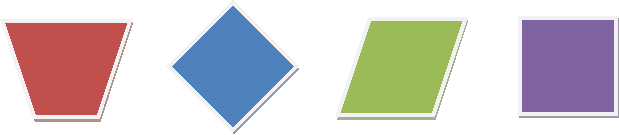
Согласно методике, практически каждое геометрическое понятие на уроках математики в начальной школе вводится наглядно, через наблюдение объекта (объектов) или оперирование им (ими). Например, введение понятия «прямоугольник». Для этого учащимся предлагается проанализировать многоугольники: сравнить, выявить общее и различие.
− Какие фигуры на доске?
− Каким одним словом можно назвать данные фигуры?
− Найдите четырехугольники, у которых все углы прямые.
− Четырехугольники, у которых все углы прямые, называются прямоугольниками.
− Откройте учебник на странице 14 (М.2, Ч.2.). Прочитаем определение в рамочке.
Введение данного понятия — это пример определения понятия «через род и видовой отличие» − явное определение. Такое введение понятия «прямоугольник» раскрывает родственные связи между данным понятием и понятием «четырехугольник». Аналогично вводится понятие «квадрат».
Такая последовательность изучения различных видов многоугольников формирует у младших школьников умение определять место каждого в данном ряду; соотносить новую фигуру с уже знакомой, а значит, осознанно выстраивать определение каждой последующей фигуры; позволяет учащимся выстроить «иерархическую лестницу» между понятиями: многоугольник, четырехугольник, прямоугольник, квадрат.
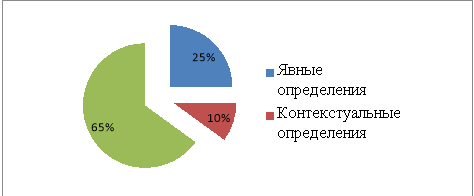
Таким образом, анализ методов и приемов введения понятий начального курса математики позволяет сделать вывод о наличии различных видов определений, где выбор каждого из них во многом определяется сложностью самого математического понятия, психолого-педагогическими и возрастными особенностями ребенка младшего школьного возраста, его готовностью к изучению каждого конкретного понятия. Процентное соотношение явных и неявных определений понятий различно у разных авторов. Так, анализ видов определений геометрических понятий, представленных в программе М.И. Моро, и их соотношение между собой можно отразить в диаграмме (рис.2) .
Рис. 2. Виды геометрических определений
Как показывает педагогическая практика, знания, умения и опыт, которые получают младшие школьники в процессе такой работы, достаточно активно, и, что самое главное, успешно используются в построении рассуждений при определении понятий не только при изучении математики, но и других учебных предметов начальной школы.
- Войшвилло Е.К Логика: Учеб. для студ. высш. учеб. заведений. / Е. К. Войшвилло, М. Г. Дегтярев — М.: Изд-во ВЛАДОС-ПРЕСС, 2001.
- Ивин А. А. Словарь по логике / И. И. Ивин, А. Л. Никифоров — М.: Гуманит. изд. центр ВЛАДОС, 1997.
- Моро М. И. Математика. 1 класс. Учеб. для общеобразоват. Организаций. В 2 ч. Ч.1 / М. И. Моро, С. И. Волкова, С. В. Степанова. М.: Просвещение, 2015.
- Моро М. И. Математика. 2 класс. Учеб. для общеобразоват. Организаций. В 2 ч. Ч.1 / М. И. Моро, С. И. Волкова, С. В. Степанова. М.: Просвещение, 2015.
Источник