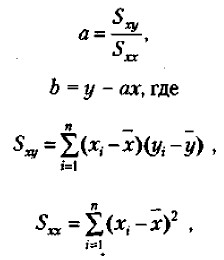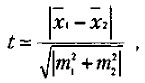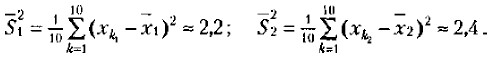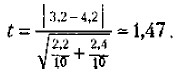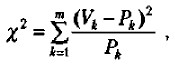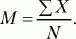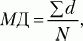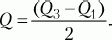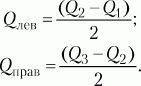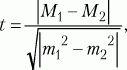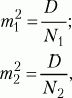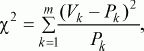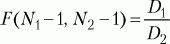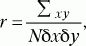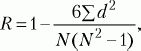Методы вторичной статистической обработки результатов эксперимента
С помощью вторичных методов статистический обработки экспериментальных данных непосредственно проверяются, доказываются или опровергаются гипотезы, связанные с экспериментом. Эти методы, как правило, сложнее, чем методы первичной статистической обработки, и требуют от исследователя хорошей подготовки в области элементарной математики и статистики.
Обсуждаемую группу методов можно разделить на несколько подгрупп: 1. Регрессионное исчисление. 2. Методы сравнения между собой двух или нескольких элементарных статистик (средних, дисперсий и т.п.), относящихся к разным выборкам. 3. Методы установления статистических взаимосвязей между переменными, например их корреляции друг с другом. 4. Методы выявления внутренней статистической структуры эмпирических данных (например, факторный анализ). Рассмотрим каждую из выделенных подгрупп методов вторичной статистической обработки на примерах.
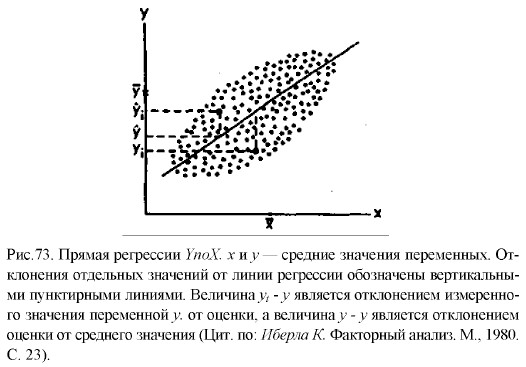
Регрессионное исчисление — это метод математической статистики, позволяющий свести частные, разрозненные данные к некоторому линейному графику, приблизительно отражающему их внутреннюю взаимосвязь, и получить возможность по значению одной из переменных приблизительно оценивать вероятное значение другой переменной.
Воспользуемся для графического представления взаимосвязанных значений двух переменных х и у точками на графике (рис. 73). Поставим перед собой задачу: заменить точки на графике линией прямой регрессии, наилучшим образом представляющей взаимосвязь, существующую между данными переменными. Иными словами, задача заключается в том, чтобы через скопление точек, имеющихся на этом графике, провести прямую линию, пользуясь которой по значению одной из переменных, х или у, можно приблизительно судить о значении другой переменной. Для того чтобы решить эту задачу, необходимо правильно найти коэффициенты а и b в уравнении искомой прямой:
Это уравнение представляет прямую на графике и называется уравнением прямой регрессии.
Формулы для подсчета коэффициентов а и b являются следующими:
где х., у1 — частные значения переменных X и Y, которым соответствуют точки на графике;
х, у — средние значения тех же самых переменных; n — число первичных значений или точек на графике.
Для сравнения выборочных средних величин, принадлежащих к двум совокупностям данных, и для решения вопроса о том, отличаются ли средние значения статистически достоверно друг от друга, нередко используют t-критерий Стъюдента. Его основная формула выглядит следующим образом:
где x1 — среднее значение переменной по одной выборке данных;
х2 — среднее значение переменной по другой выборке данных;
m1 и m2 — интегрированные показатели отклонений частных значений из двух сравниваемых выборок от соответствующих им средних величин.
m1, и m2 в свою очередь вычисляются по следующим формулам:
где 

n1, — число частных значений переменной в первой выборке;
n2 — число частных значений переменной по второй выборке.
После того как при помощи приведенной выше формулы вычислен показатель t, по таблице 32 для заданного числа степеней свободы, равного n1 + n2 — 2, и избранной вероятности допустимой ошибки 1 находят нужное табличное значение t и сравнивают с ними вычисленное значение t.
1 Степени свободы и вероятность допустимой ошибки — специальные математико-статистические термины, содержание которых мы здесь не будем рассматривать.
Если вычисленное значение t больше или равно табличному, то делают вывод о том, что сравниваемые средние значения из двух выборок действительно статистически достоверно различаются с вероятностью допустимой ошибки, меньшей или равной избранной. Рассмотрим процедуру вычисления t-критерия Стъюдента и определения на его основе разницы в средних величинах на конкретном примере. Допустим, что имеются следующие две выборки экспериментальных данных: 2, 4, 5, 3, 2, 1, 3, 2, 6, 4, и 4, 5, 6, 4, 4, 3, 5, 2, 2, 7.
Средние значения по этим двум выборкам соответственно равны 3,2 и 4,2. Кажется, что они существенно друг от друга отличаются. Но так ли это и насколько статистически достоверны эти различия? На данный вопрос может точно ответить только статистический анализ с использованием описанного статистического критерия. Воспользуемся этим критерием.
Определим сначала выборочные дисперсии для двух сравниваемых выборок значений:
Поставим найденные значения дисперсий в формулу для подсчета m a t к вычислим показатель t
Сравним его значение с табличным для числа степеней свободы 10 + 10 — 2 = 18. Зададим вероятность допустимой ошибки, равной 0,05, и убедимся в том, что для данного числа степеней свободы и заданной вероятности допустимой ошибки значение t должно быть не меньше чем 2,10. У нас же этот показатель оказался равным 1,47, т.е. меньше табличного. Следовательно, гипотеза о том, что выборочные средние, равные в нашем случае 3,2 и 4,2, статистически достоверно отличаются друг от друга, не подтвердилась, хотя на первый взгляд казалось, что такие различия существуют.
Вероятность допустимой ошибки, равная и меньшая чем 0,05, считается достаточной для научно убедительных выводов. Чем меньше эта вероятность, тем точнее и убедительнее делаемые выводы. Например, избрав вероятность допустимой ошибки, равную 0,05, мы обеспечиваем точность расчетов 95% и допускаем ошибку, не превышающую 5%, а выбор вероятности допустимой ошибки 0,001 гарантирует точность расчетов, превышающую 99,99%, или ошибку, меньшую чем 0,01%.
Описанная методика сравнения средних величин по критерию Стъюдента в практике применяется тогда, когда необходимо, например, установить, удался или не удался эксперимент, оказал или не оказал он влияние на уровень развития того психологического качества, для изменения которого предназначался. Допустим, что в некотором учебном заведении вводится новая экспериментальная программа или методика обучения, рассчитанная на то, чтобы улучшить знания учащихся, повысить уровень их интеллектуального развития. В этом случае выясняется причинно-следственная связь между независимой переменной — программой или методикой и зависимой переменной — знаниями или уровнем интеллектуального развития. Соответствующая гипотеза гласит: «Введение новой учебной программы или методики обучения должно будет существенно улучшить знания или повысить уровень интеллектуального развития учащихся».
Предположим, что данный эксперимент проводится по схеме, предполагающей оценки зависимой переменной в начале и в конце эксперимента. Получив такие оценки и вычислив средние по всей изученной выборке испытуемых, мы можем воспользоваться критерием Стъюдента для точного установления наличия или отсутствия статистически достоверных различий между средними до и после эксперимента. Если окажется, что они действительно достоверно различаются, то можно будет сделать определенный вывод о том, что эксперимент удался. В противном случае нет убедительных оснований для такого вывода даже в том случае, если сами средние величины в начале и в конце эксперимента по своим абсолютным значениям различны.
Иногда в процессе проведения эксперимента возникает специальная задача сравнения не абсолютных средних значений некоторых величин до и после эксперимента, а частотных, например процентных, распределений данных. Допустим, что для экспериментального исследования была взята выборка из 100 учащихся и с ними проведен формирующий эксперимент. Предположим также, что до эксперимента 30 человек успевали на «удовлетворительно», 30 — на «хорошо», а остальные 40 — на «отлично». После эксперимента ситуация изменилась. Теперь на «удовлетворительно» успевают только 10 учащихся, на «хорошо» — 45 учащихся и на «отлично» — остальные 45 учащихся. Можно ли, опираясь на эти данные, утверждать, что формирующий эксперимент, направленный на улучшение успеваемости, удался? Для ответа на данный вопрос можно воспользоваться статистикой, называемой х 2 -критерий («хи-квадрат критерий»). Его формула выглядит следующим образом:
где Рк — частоты результатов наблюдений до эксперимента;
Vk — частоты результатов наблюдений, сделанных после эксперимента;
m — общее число групп, на которые разделились результаты наблюдений.
Воспользуемся приведенным выше примером для того, чтобы показать, как работает хи-квадрат критерий. В данном примере переменная Рк принимает следующие значения: 30%, 30%, 40%, а переменная Vk—такие значения: 10%, 45%, 45%.
Источник
Способы вторичной статистической обработки результатов исследования
7.1. Общее представление об обработке данных
Обработка данных психологических исследований – отдельный раздел экспериментальной психологии, тесно связанный с математической статистикой и логикой. Обработка данных направлена на решение следующих задач:
• упорядочивание полученного материала;
• обнаружение и ликвидация ошибок, недочетов, пробелов в сведениях;
• выявление скрытых от непосредственного восприятия тенденций, закономерностей и связей;
• обнаружение новых фактов, которые не ожидались и не были замечены в ходе эмпирического процесса;
• выяснение уровня достоверности, надежности и точности собранных данных и получение на их базе научно обоснованных результатов.
Различают количественную и качественную обработку данных. Количественная обработка – это работа с измеренными характеристиками изучаемого объекта, его «объективированными» свойствами. Качественная обработка представляет собой способ проникновения в сущность объекта путем выявления его неизмеряемых свойств.
Количественная обработка направлена в основном на формальное, внешнее изучение объекта, качественная – преимущественно на содержательное, внутреннее его изучение. В количественном исследовании доминирует аналитическая составляющая познания, что отражено и в названиях количественных методов обработки эмпирического материала: корреляционный анализ, факторный анализ и т. д. Реализуется количественная обработка с помощью математико-статистических методов.
В качественной обработке преобладают синтетические способы познания. Обобщение проводится на следующем этапе исследовательского процесса – интерпретационном. При качественной обработке данных главное заключается в соответствующем представлении сведений об изучаемом явлении, обеспечивающем дальнейшее его теоретическое изучение. Обычно результатом качественной обработки является интегрированное представление о множестве свойств объекта или множестве объектов в форме классификаций и типологий. Качественная обработка в значительной мере апеллирует к методам логики.
Противопоставление друг другу качественной и количественной обработки довольно условно. Количественный анализ без последующей качественной обработки бессмыслен, так как сам по себе не приводит к приращению знаний, а качественное изучение объекта без базовых количественных данных в научном познании невозможно. Без количественных данных научное познание – чисто умозрительная процедура.
Единство количественной и качественной обработки наглядно представлено во многих методах обработки данных: факторном и таксономическом анализе, шкалировании, классификации и др. Наиболее распространены такие приемы количественной обработки, как классификация, типологизация, систематизация, периодизация, казуистика.
Качественная обработка естественным образом выливается в описание и объяснение изучаемых явлений, что составляет уже следующий уровень их изучения, осуществляемый на стадии интерпретации результатов. Количественная же обработка полностью относится к этапу обработки данных.
7.2. Первичная статистическая обработка данных
Все методы количественной обработки принято подразделять на первичные и вторичные.
Первичная статистическая обработка нацелена на упорядочивание информации об объекте и предмете изучения. На этой стадии «сырые» сведения группируются по тем или иным критериям, заносятся в сводные таблицы. Первично обработанные данные, представленные в удобной форме, дают исследователю в первом приближении понятие о характере всей совокупности данных в целом: об их однородности – неоднородности, компактности – разбросанности, четкости – размытости и т. д. Эта информация хорошо считывается с наглядных форм представления данных и дает сведения об их распределении.
В ходе применения первичных методов статистической обработки получаются показатели, непосредственно связанные с производимыми в исследовании измерениями.
К основным методам первичной статистической обработки относятся: вычисление мер центральной тенденции и мер разброса (изменчивости) данных.
Первичный статистический анализ всей совокупности полученных в исследовании данных дает возможность охарактеризовать ее в предельно сжатом виде и ответить на два главных вопроса: 1) какое значение наиболее характерно для выборки; 2) велик ли разброс данных относительно этого характерного значения, т. е. какова «размытость» данных. Для решения первого вопроса вычисляются меры центральной тенденции, для решения второго – меры изменчивости (или разброса). Эти статистические показатели используются в отношении количественных данных, представленных в порядковой, интервальной или пропорциональной шкале.
Меры центральной тенденции – это величины, вокруг которых группируются остальные данные. Данные величины являются как бы обобщающими всю выборку показателями, что, во-первых, позволяет судить по ним обо всей выборке, а во-вторых, дает возможность сравнивать разные выборки, разные серии между собой. К мерам центральной тенденции в обработке результатов психологических исследований относятся: выборочное среднее, медиана, мода.
Выборочное среднее (М) – это результат деления суммы всех значений (X) на их количество (N).
Медиана (Me) – это значение, выше и ниже которого количество отличающихся значений одинаково, т. е. это центральное значение в последовательном ряду данных. Медиана не обязательно должна совпадать с конкретным значением. Совпадение происходит в случае нечетного числа значений (ответов), несовпадение – при четном их числе. В последнем случае медиана вычисляется как среднее арифметическое двух центральных значений в упорядоченном ряду.
Мода (Мо) – это значение, наиболее часто встречающееся в выборке, т. е. значение с наибольшей частотой. Если все значения в группе встречаются одинаково часто, то считается, что моды нет. Если два соседних значения имеют одинаковую частоту и больше частоты любого другого значения, мода есть среднее этих двух значений. Если то же самое относится к двум несмежным значениям, то существует две моды, а группа оценок является бимодальной.
Обычно выборочное среднее применяется при стремлении к наибольшей точности в определении центральной тенденции. Медиана вычисляется в том случае, когда в серии есть «нетипичные» данные, резко влияющие на среднее. Мода используется в ситуациях, когда не нужна высокая точность, но важна быстрота определения меры центральной тенденции.
Вычисление всех трех показателей производится также для оценки распределения данных. При нормальном распределении значения выборочного среднего, медианы и моды одинаковы или очень близки.
Меры разброса (изменчивости) – это статистические показатели, характеризующие различия между отдельными значениями выборки. Они позволяют судить о степени однородности полученного множества, его компактности, а косвенно и о надежности полученных данных и вытекающих из них результатов. Наиболее используемые в психологических исследованиях показатели: среднее отклонение, дисперсия, стандартное отклонение.
Размах (Р) – это интервал между максимальным и минимальным значениями признака. Определяется легко и быстро, но чувствителен к случайностям, особенно при малом числе данных.
Среднее отклонение (МД) – это среднеарифметическое разницы (по абсолютной величине) между каждым значением в выборке и ее средним.
где d = |Х – М |, М – среднее выборки, X – конкретное значение, N – число значений.
Множество всех конкретных отклонений от среднего характеризует изменчивость данных, но если не взять их по абсолютной величине, то их сумма будет равна нулю и мы не получим информации об их изменчивости. Среднее отклонение показывает степень скученности данных вокруг выборочного среднего. Кстати, иногда при определении этой характеристики выборки вместо среднего (М) берут иные меры центральной тенденции – моду или медиану.
Дисперсия (D) характеризует отклонения от средней величины в данной выборке. Вычисление дисперсии позляет избежать нулевой суммы конкретных разниц (d = Х – М) не через их абсолютные величины, а через их возведение в квадрат:
где d = |Х – М|, М – среднее выборки, X – конкретное значение, N – число значений.
Стандартное отклонение (б). Из-за возведения в квадрат отдельных отклонений d при вычислении дисперсии полученная величина оказывается далекой от первоначальных отклонений и потому не дает о них наглядного представления. Чтобы этого избежать и получить характеристику, сопоставимую со средним отклонением, проделывают обратную математическую операцию – из дисперсии извлекают квадратный корень. Его положительное значение и принимается за меру изменчивости, именуемую среднеквадратическим, или стандартным, отклонением:
где d = |Х– М|, М – среднее выборки, X– конкретное значение, N – число значений.
МД, D и ? применимы для интервальных и пропорционных данных. Для порядковых данных в качестве меры изменчивости обычно берут полуквартильное отклонение (Q), именуемое еще полуквартильным коэффициентом. Вычисляется этот показатель следующим образом. Вся область распределения данных делится на четыре равные части. Если отсчитывать наблюдения начиная от минимальной величины на измерительной шкале, то первая четверть шкалы называется первым квартилем, а точка, отделяющая его от остальной части шкалы, обозначается символом Qv Вторые 25 % распределения – второй квартиль, а соответствующая точка на шкале – Q2. Между третьей и четвертой четвертями распределения расположена точка Q3. Полуквартильный коэффициент определяется как половина интервала между первым и третьим квартилями:
При симметричном распределении точка Q2 совпадет с медианой (а следовательно, и со средним), и тогда можно вычислить коэффициент Q для характеристики разброса данных относительно середины распределения. При несимметричном распределении этого недостаточно. Тогда дополнительно вычисляют коэффициенты для левого и правого участков:
7.3. Вторичная статистическая обработка данных
К вторичным относят такие методы статистической обработки, с помощью которых на базе первичных данных выявляют скрытые в них статистические закономерности. Вторичные методы можно подразделить на способы оценки значимости различий и способы установления статистических взаимосвязей.
Способы оценки значимости различий. Для сравнения выборочных средних величин, принадлежащих к двум совокупностям данных, и для решения вопроса о том, отличаются ли средние значения статистически достоверно друг от друга, используют t-критерий Стьюдента. Его формула выглядит следующим образом:
где М1, М2 – выборочные средние значения сравниваемых выборок, m1, m2 – интегрированные показатели отклонений частных значений из двух сравниваемых выборок, вычисляются по следующим формулам:
где D1, D2 – дисперсии первой и второй выборок, N1, N2 – число значений в первой и второй выборках.
После вычисления значения показателя t по таблице критических значений (см. Статистическое приложение 1), заданного числа степеней свободы (N1 + N2 – 2) и избранной вероятности допустимой ошибки (0,05, 0,01, 0,02, 001 и т.д.) находят табличное значение t. Если вычисленное значение t больше или равно табличному, делают вывод о том, что сравниваемые средние значения двух выборок статистически достоверно различаются с вероятностью допустимой ошибки, меньшей или равной избранной.
Если в процессе исследования встает задача сравнить неабсолютные средние величины, частотные распределения данных, то используется ?2критерий (см. Приложение 2). Его формула выглядит следующим образом:
где Pk – частоты распределения в первом замере, Vk – частоты распределения во втором замере, m – общее число групп, на которые разделились результаты замеров.
После вычисления значения показателя ?2по таблице критических значений (см. Статистическое приложение 2), заданного числа степеней свободы (m – 1) и избранной вероятности допустимой ошибки (0,05, 0,0 ?2t больше или равно табличному) делают вывод о том, что сравниваемые распределения данных в двух выборках статистически достоверно различаются с вероятностью допустимой ошибки, меньшей или равной избранной.
Для сравнения дисперсий двух выборок используется F-критерий Фишера. Его формула выглядит следующим образом:
где D1, D2 – дисперсии первой и второй выборок, N1, N2 – число значений в первой и второй выборках.
После вычисления значения показателя F по таблице критических значений (см. Статистическое приложение 3), заданного числа степеней свободы (N1 – 1, N2 – 1) находится Fкр. Если вычисленное значение F больше или равно табличному, делают вывод о том, что различие дисперсий в двух выборках статистически достоверно.
Способы установления статистических взаимосвязей. Предыдущие показатели характеризуют совокупность данных по какому-либо одному признаку. Этот изменяющийся признак называют переменной величиной или просто переменной. Меры связи выявляют соотношения между двумя переменными или между двумя выборками. Эти связи, или корреляции, определяют через вычисление коэффициентов корреляции. Однако наличие корреляции не означает, что между переменными существует причинная (или функциональная) связь. Функциональная зависимость – это частный случай корреляции. Даже если связь причинна, корреляционные показатели не могут указать, какая из двух переменных является причиной, а какая – следствием. Кроме того, любая обнаруженная в психологических исследованиях связь, как правило, существует благодаря и другим переменным, а не только двум рассматриваемым. К тому же взаимосвязи психологических признаков столь сложны, что их обусловленность одной причиной вряд ли состоятельна, они детерминированы множеством причин.
По тесноте связи можно выделить следующие виды корреляции: полная, высокая, выраженная, частичная; отсутствие корреляции. Эти виды корреляций определяют в зависимости от значения коэффициента корреляции.
При полной корреляции его абсолютные значения равны или очень близки к 1. В этом случае устанавливается обязательная взаимозависимость между переменными. Здесь вероятна функциональная зависимость.
Высокая корреляция устанавливается при абсолютном значении коэффициента 0,8–0,9. Выраженная корреляция считается при абсолютном значении коэффициента 0,6–0,7. Частичная корреляция существует при абсолютном значении коэффициента 0,4–0,5.
Абсолютные значения коэффициента корреляции менее 0,4 свидетельствуют об очень слабой корреляционной связи и, как правило, в расчет не принимаются. Отсутствие корреляции констатируется при значении коэффициента 0.
Кроме того, в психологии при оценке тесноты связи используют так называемую «частную» классификацию корреляционных связей. Она ориентирована не на абсолютную величину коэффициентов корреляции, а на уровень значимости этой величины при определенном объеме выборки. Эта классификация применяется при статистической оценке гипотез. При данном подходе предполагается, что чем больше выборка, тем меньшее значение коэффициента корреляции может быть принято для признания достоверности связей, а для малых выборок даже абсолютно большое значение коэффициента может оказаться недостоверным.[86]
По направленности выделяют следующие виды корреляционных связей: положительная (прямая) и отрицательная (обратная). Положительная (прямая) корреляционная связь регистрируется при коэффициенте со знаком «плюс»: при увеличении значения одной переменной наблюдается увеличение другой. Отрицательная (обратная) корреляция имеет место при значении коэффициента со знаком «минус». Это означает обратную зависимость: увеличение значения одной переменной влечет за собой уменьшение другой.
По форме различают следующие виды корреляционных связей: прямолинейную и криволинейную. При прямолинейной связи равномерным изменениям одной переменной соответствуют равномерные изменения другой. Если говорить не только о корреляциях, но и о функциональных зависимостях, то такие формы зависимости называют пропорциональными. В психологии строго прямолинейные связи – явление редкое. При криволинейной связи равномерное изменение одного признака сочетается с неравномерным изменением другого. Эта ситуация для психологии типична.
Коэффициент линейной корреляции по К. Пирсону (r) вычисляется c помощью следующей формулы:
где х – отклонение отдельного значения X от среднего выборки (Мх), у – отклонение отдельного значения Y от среднего выборки (Му), Ьх – стандартное отклонение для X, ?y – стандартное отклонение для Y, N – число пар значений Xи Y.
Оценка значимости коэффициента корреляции проводится по таблице (см. Статистическое приложение 4).
При сравнении порядковых данных применяется коэффициент ранговой корреляции по Ч. Спирмену (R):
где d – разность рангов (порядковых мест) двух величин, N – число сравниваемых пар величин двух переменных (X и Y).
Оценка значимости коэффициента корреляции проводится по таблице (см. Статистическое приложение 5).
Внедрение в научные исследования автоматизированных средств обработки данных позволяет быстро и точно определять любые количественные характеристики любых массивов данных. Разработаны различные программы для компьютеров, по которым можно проводить соответствующий статистический анализ практически любых выборок. Из массы статистических приемов в психологии наибольшее распространение получили следующие: 1) комплексное вычисление статистик; 2) корреляционный анализ; 3) дисперсионный анализ; 4) регрессионный анализ; 5) факторный анализ; 6) таксономический (кластерный) анализ; 7) шкалирование. Познакомиться с характеристиками этих методов можно в специальной литературе («Статистические методы в педагогике и психологии» Стенли Дж., Гласа Дж. (М., 1976), «Математическая психология» Г.В. Суходольского (СПб., 1997), «Математические методы психологического исследования» А.Д. Наследова (СПб., 2005) и др.).
Источник