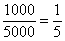Способы вторичной группировки данных
3.5 чФПТЙЮОБС ЗТХРРЙТПЧЛБ
ч УМХЮБЕ ЛПЗДБ ТБОЕЕ РПУФТПЕООБС ЗТХРРЙТПЧЛБ ОЕ УППФЧЕФУФЧХЕФ ГЕМСН ЙУУМЕДПЧБОЙС Й УПЧТЕНЕООПНХ ИБТБЛФЕТХ ТБУРТЕДЕМЕОЙС ЕДЙОЙГ УПЧПЛХРОПУФЙ , РТПЧПДСФ ЧФПТЙЮОХА ЗТХРРЙТПЧЛХ .
пОБ РТЕДУФБЧМСЕФ УПВПК РТПГЕУУ РЕТЕЗТХРРЙТПЧЛЙ ДБООЩИ ДМС МХЮЫЕК ИБТБЛФЕТЙУФЙЛЙ ЙЪХЮБЕНПЗП СЧМЕОЙС ,РТЙ РТПЧЕДЕОЙЙ УТБЧОЙФЕМШОПЗП БОБМЙЪБ. уХФШ ДБООПЗП НЕФПДБ ЪБЛМАЮБЕФУС Ч РЕТЕЗТХРРЙТПЧЛЕ ЕДЙОЙГ ПВЯЕЛФБ ВЕЪ ПВТБЭЕОЙС Л РЕТЧЙЮОЩН ДБООЩН. оБ ПУОПЧЕ ТБОЕЕ РТПЧЕДЕООЩИ ЗТХРРЙТПЧПЛ ПВТБЪХАФ ОПЧЩЕ ЗТХРРЩ ЪБ УЮЕФ ПВЯЕДЙОЕОЙС РЕТЧПОБЮБМШОЩИ ЙОФЕТЧБМПЧ ЙМЙ ЪБ УЮЕФ ДПМЕЧПК РЕТЕЗТХРРЙТПЧЛЙ У ПРТЕДЕМЕООПК ДПМЕК ЕДЙОЙГ УПЧПЛХРОПУФЙ.
тБУУНПФТЙН НЕФПДЙЛХ РТПЧЕДЕОЙС ЧФПТЙЮОПК ЗТХРРЙТПЧЛЙ ОБ РТЙНЕТЕ ТБУРТЕДЕМЕОЙС ТБВПЮЙИ УФТПЙФЕМШОПК ПТЗБОЙЪБГЙЙ РП ТБЪНЕТХ ЪБТБВПФОПК РМБФЩ.
рЕТЧЩН ОБЙВПМЕЕ РТПУФЩН УРПУПВПН РПУФТПЕОЙС ЧФПТЙЮОПК ЗТХРРЙТПЧЛЙ СЧМСЕФУС ПВЯЕДЙОЕОЙЕ РЕТЧПОБЮБМШОЩИ ЙОФЕТЧБМПЧ (ХЛТХРОЕОЙЕ ЙОФЕТЧБМПЧ). тБУУНПФТЙН ЬФП ОБ РТЙНЕТЕ ДЧХИ РПУМЕДХАЭЙИ ФБВМЙГ (3.12 Й 3.13).
тБУРТЕДЕМЕОЙЕ ТБВПЮЙИ РП ЪБТБВПФОПК РМБФЕ
| вТЙЗБДБ N 1 | вТЙЗБДБ N 2 | ||
| ъБТБВПФБООБС РМБФБ, ТХВ. | юЙУМП ТБВПЮЙИ, ЮЕМ. | ъБТБВПФБООБС РМБФБ, ТХВ. | юЙУМП ТБВПЮЙИ, ЮЕМ. |
| ДП 500 ПФ 500 ДП 1000 ПФ 1000 ДП 1500 ПФ 1500 ДП 2000 ПФ 2000 ДП 2500 ПФ 2500 ДП 3000 ПФ 3000 ДП 3500 ПФ 3500 ДП 4000 | 1 4 7 8 6 3 1 1 | ДП 600 ПФ 600 ДП 1000 ПФ 1000 ДП 2000 ПФ 2000 ДП 3000 ПФ 3000 ДП 4000 ПФ 4500 ДП 5000 | 2 3 5 12 8 2 |
рП ЮЙУМХ ЗТХРР Й ЧЕМЙЮЙОЕ ЙОФЕТЧБМПЧ ТБУРТЕДЕМЕОЙЕ ТБВПЮЙИ ДЧХИ ВТЙЗБД ТБЪМЙЮОПЕ. юФПВЩ УДЕМБФШ ДБООЩЕ УПРПУФБЧЙНЩНЙ РТПЙЪЧЕДЕН ЧФПТЙЮОХА ЗТХРРЙТПЧЛХ ПВТБЪПЧБЧ Ч ЛБЦДПК ВТЙЗБДЕ ФТЙ ЗТХРРЩ У ЪБТБВПФОПК РМБФПК ТБВПЮЙИ:
ДП 2000 ТХВ.
ПФ 2000 ТХВ. ДП 4000 ТХВ.
ПФ 4000 ТХВ. Й ЧЩЫЕ.
чФПТЙЮОБС ЗТХРРЙТПЧЛБ, РТПЧЕДЕООБС РП НЕФПДХ ПВЯЕДЙОЕОЙС ЙОФЕТЧБМПЧ РТЙНЕФ УМЕДХАЭЙК ЧЙД:
зТХРРЙТПЧЛБ ТБВПЮЙИ УФТПЙФЕМШОПК ПТЗБОЙЪБГЙЙ
РП ЪБТБВПФОПК РМБФЕ
| N ЗТ. | зТХРРЩ ТБВПЮЙИ У ЪБТБВПФОПК РМБФПК, ТХВ. | чУЕЗП ТБВПЮЙИ, ЮЕМ. | ч ФПН ЮЙУМЕ | |
| ВТЙЗБДБ N 1 | ВТЙЗБДБ N 2 | |||
| 1 | ДП 2000 | 30 | 20 | 10 |
| 2 | ПФ 2000 ДП 4000 | 31 | 11 | 20 |
| 3 | ПФ 4000 Й ЧЩЫЕ | 2 | — | 2 |
| йфпзп | 63 | 31 | 32 | |
йЪ ФБВМЙГЩ УМЕДХЕФ, ЮФП ЮЙУМЕООПУФШ ТБВПЮЙИ У ОЙЪЛПК ЪБТБВПФОПК РМБФПК ВПМШЫЕ Ч РЕТЧПК ВТЙЗБДЕ, Б У ЧЩУПЛПК ЪБТБВПФОПК РМБФПК ЧП ЧФПТПК ВТЙЗБДЕ.
вПМЕЕ УМПЦОЩН СЧМСЕФУС УРПУПВ ДПМЕЧПК РЕТЕЗТХРРЙТПЧЛЙ (ФБВМ. 3.14.)
тБУРТЕДЕМЕОЙЕ ТБВПЮЙИ УФТПЙФЕМШОПК ПТЗБОЙЪБГЙЙ РП ЪБТБВПФОПК РМБФЕ
| зТХРРЩ ТБВПЮЙИ РП ЪБТБВПФОПК РМБФЕ, ТХВ. | юЙУМП ТБВПЮЙИ, ЮЕМ. |
| ДП 600 ПФ 600 ДП 1200 ПФ 1200 ДП 2000 ПФ 2000 ДП 3200 ПФ 3200 ДП 4600 ПФ 4600 Й ВПМЕЕ | 12 18 25 36 6 3 |
| йфпзп | 100 |
рТПЙЪЧЕДЕН РЕТЕЗТХРРЙТПЧЛХ ДБООЩИ ПВТБЪПЧБЧ ОПЧЩЕ ЗТХРРЩ У ЙОФЕТЧБМБНЙ: ДП 1000, 1000-1200, 2000-3000, 3000-4000, ПФ 4000 Й ЧЩЫЕ.
ч РЕТЧХА ОПЧХА ЗТХРРХ ЧПКДЕФ РПМОПУФША РЕТЧБС ЗТХРРБ Й ЮБУФШ ЧФПТПК ЗТХРРЩ. юФПВЩ ПВТБЪПЧБФШ ЗТХРРХ ДП 1000 ТХВ., ОЕПВИПДЙНП ПФ ЙОФЕТЧБМБ ЧФПТПК ЗТХРРЩ ЧЪСФШ 400 ТХВ. чЕМЙЮЙОБ ЙОФЕТЧБМБ ЬФПК ЗТХРРЩ УПУФБЧМСЕФ 600 ТХВ. уМЕДПЧБФЕМШОП, ОЕПВИПДЙНП ЧЪСФШ ПФ ОЕЕ 4/6 (400/600) ЮБУФЕК. бОБМПЗЙЮОХА ЮБУФШ ОБДП ЧЪСФШ Й ПФ ЮЙУМЕООПУФЙ ТБВПФБАЭЙИ, Ф.Е. 18ћ4/6=11,8(12) ЮЕМ. фПЗДБ Ч РЕТЧПК ЗТХРРЕ ВХДЕФ ТБВПФБАЭЙИ 12+12=24 ЮЕМПЧЕЛБ Й Ф.Д.
ч ТЕЪХМШФБФЕ РПМХЮЙН ФБВМЙГХ У НЕОШЫЙН ЛПМЙЮЕУФЧПН ЗТХРР, ТБУУЮЙФБООХА УРПУПВПН ДПМЕЧПК РЕТЕЗТХРРЙТПЧЛЙ.
тБУРТЕДЕМЕОЙЕ ТБВПЮЙИ РП ЪБТБВПФОПК РМБФЕ
| зТХРРЩ ТБВПЮЙИ РП ЪБТБВПФОПК РМБФЕ, ТХВ. | юЙУМП ТБВПЮЙИ, ЮЕМ. |
| ДП 1000 ПФ 1000 ДП 2000 ПФ 2000 ДП 3000 ПФ 3000 ДП 4000 ПФ 4000 Й ЧЩЫЕ | 24 32 30 10 4 |
| йфпзп | 100 |
йЪ ФБВМЙГЩ УМЕДХЕФ, ЮФП ВПМШЫЙОУФЧП ТБВПЮЙИ РПМХЮБАФ ОЕЧЩУПЛХА ЪБТБВПФОХА РМБФХ Ч ТБЪНЕТЕ ДП 3000 ТХВМЕК.
Источник
Способы вторичной группировки данных
Тема3: Сводка и группировка статистических материалов.
3.1 Содержание и задача сводки. Этапы сводки.
3.2 Статистические группировки. Виды группировок.
3.3 Группировочные признаки и их выбор. Определение числа групп и величины интервала.
3.4 Вторичная группировка.
3.5 Ряды распределения. Их виды.
3.6 Статистические таблицы.
3.1 Содержание и задача сводки. Этапы сводки.
В результате статистического наблюдения получают материал, характеризующий отдельные единицы совокупности. Эти единицы обладают многочисленными признаками, поэтому невозможно использовать материал наблюдения для обобщающей характеристики статистической совокупности. Возникает необходимость специальной обработки статистических данных, т.е. сводки материалов наблюдения.
Сводка представляет собой комплекс последовательных действий по обобщению конкретных единичных данных, образующих совокупность в целях выявления типических черт и закономерностей, присущих изучаемому явлению в целом.
Задачи сводки:
1) Охарактеризовать исследуемую совокупность с помощью систем статистических показателей;
2) Выявить и измерить таким путем его существенные черты и особенности.
Эта задача решается на 3 этапах:
1этап. Осуществляется систематизация материалов, собранных при наблюдении.
2этап. Уточняется предусмотренная планом система показателей, с помощью которых количественно характеризуются свойства и особенности изучаемого предмета.
3этап. Проводятся расчеты, а затем рассчитанные показатели для наглядности представляются в таблицах, статистических рядах, графиках. К ним даются пояснения (делается анализ представленных данных).
3.2 Статистические группировки. Виды группировок.
Чаще всего простые итоговые данные сводки не удовлетворяют исследователя, т.к. дают лишь общее представление об изучаемом объекте. Поэтому далее проводят группировку полученных данных по отдельным признакам.
Группировка – это разделение множества единиц совокупности на однородные группы по определенным, существенным для них, признакам.
Как самостоятельный метод исследования она позволяет решить три основные задачи:
1) выделить социально-экономические типы; 2) изучить структуру однотипной совокупности; 3) обнаружить существенные связи и зависимость между признаками.
В соответствии с этими задачами группировки подразделяются на 3 вида: типологические, структурные и аналитичекие.
1) Типологические группировки – это разделение исследуемой совокупности на социально-экономические типы, однородные группы единиц в соответствии с правилами научного группировки. Например, группировка стран по их общественно-полическому устройству.
2) Структурные группировки — это разделение однородной совокупности единиц на группы, характеризующие её структуру по определенным признакам. Например, перепись населения.
3) Аналитические группировки – позволяют установить и изучить связь между результативными и факторными признаками единиц однотипной совокупности.
Результативные признаки – это признаки, зависимые от других признаков ОПП=ЧР ГВ
Факторные признаки – это признаки, оказывающие влияние на другие признаки (численность рабочих, среднегодовая выработка).
Кроме того по степени сложности изучаемого массового явления и от задач анализа группировки могут производиться по одному признаку (простые группировки) или по нескольким признакам (комбинированные).
3.3 Группировочные признаки и их выбор. Определение числа групп и величины интервала.
Одним из важных элементов проведения статистических группировок является выбор группировочного признака. Группировочные признаки м.б. количественные (зарплата, возраст) и атрибутивные (т.е. не имеющие количественной меры – национальность, пол, профессии). Кроме того, по экономическому содержанию различают результативный и факторный признаки.
Результативные признаки – это признаки, зависимые от других признаков.
Факторные признаки – это признаки, оказывающие влияние на другие признаки.
При выборе группировочного признака и проведении статистических группировок необходимо руководствоваться следующими указаниями:
1) В основу типологической группировки д.б. положены наиболее существенные признаки.
2) При выделении социально-экономических типов нельзя ограничиваться только одним признаком. Необходимо брать целый комплекс существенных признаков.
3) Приёмы и способы группировки д. изменяться применительно к особенностям общественных явлений, к конкретным историческим условиям их развития.
После того, как выбран группировочный признак, определяется число групп во всей совокупности и величина интервала к каждой группе. На практике для определения числа групп используют графический и аналитический методы.
Рассмотрим аналитический метод, согласно которому число групп определяется по формуле Стерджесса:
n=1+3,322lgN
n – число групп
N – число единиц совокупности
h=(Xmax—Xmin)/n – величина интервала
Интервалы м.б. закрытые (имеют и нижние и верхние границы) открытые. Они применяются Толькой для первой и последней группировок.
Интервалы м.б. равными (ширина интервала во всех группах одна и та же) и неравные (разная ширина).
3.4 Вторичная группировка.
Группировка данных, полученных в результате статистического наблюдения — это первичная группировка. Вторичная группировка – это перегруппировка ранее сгруппированных данных. Необходимость вторичной группировки возникает в следующих случаях:
1) когда ранее проведенная группировка не удовлетворяет целям исследования в отношении числа групп;
2) для сравнения данных, относящихся к различным периодам времени или к разным территориям;
3) если первичная группировка была произведена по разным группировочным признакам или по разным интервалам.
Существует два способа проведения вторичной группировки:
1. объединение мелких групп в более крупные;
2. выделение определенной доли единиц совокупности.
3.5 Ряды распределения. Их виды.
Первичная обработка и систематизация материалов статистического наблюдения приводит к образованию упорядоченных рядов цифр.
Ряд цифровых показателей, представляющей распределение единиц совокупности по одному признаку в определенной последовательности называется рядом распределения. Ряды распределения, построенные по атрибутивному признаку, называются атрибутивными рядами распределения.
Ряды распределения, построенные по количественному признаку (варьирующему) называются вариационными рядами распределения.
Числовые значения количественного признака в вариационном ряду распределения называются вариантами и располагаются в определенной последовательности.
Варианты могут выражаться целыми числами и дробными, положительными и отрицательными, абсолютными и относительными. Пример, прибыль (+), убыток (-), % относит.
В вариационных рядах и в целом по всей совокупности выделяются три основных элемента:
1) вариант — это признак, по которому производиться группировка (х)
2) частота — это число которое показывает как часто встречается вариант в данном ряду распределения (f)
3) частость — это частоты, выраженные в виде относительных величин (% в долях едииц)
Вариационные ряды подразделяются на дискретные и интервальные.
В дискретных вариационных рядах значение вариантов отличается друг от друга на определенную величину. Варианты дискретного ряда выражаются целыми числами. Например, число членов семьи.
Источник
14. Группировка данных. Виды группировок.
Перегруппировка
Эта статья условно открывает вторую часть курса Математической статистики, и начнём мы с простенького материала, который вполне бы мог войти в 1-й урок, но оказался там немного не в тему, поскольку сам открывает большую тему 🙂
Рассмотрим некоторую статистическую совокупность, например, множество студентов ВУЗа. Очевидно, это множество можно исследовать как единое целое – подсчитать общее количество студентов, вычислить их средний возраст, среднюю успеваемость и др. характеристики. Благо, статистических данных – море. Но всё это общие характеристики. Во многих случаях совокупность целесообразно разделить на группы, то есть выполнить группировку.
Группировка – это разделение статистической совокупности (не важно, генеральной или выборочной) на группы по одному или бОльшему количеству признаков.
И разделить её можно по-разному. Во-первых, выделить качественно однородные группы. Например, разделить студентов ВУЗа на лиц М и Ж пола. Такая группировка называется типологической. Или, как вы любите говорить, «типа логической» 🙂 Кстати, студенты уже по факту разделены на факультеты – и это тоже пример типологической группировки, но уже по другому признаку.
Итак, типологическая группировка – это разделение неоднородной статистической совокупности на качественно однородные группы.
Само собой полученные группы исследуются по отдельности и сравниваются – как между собой, так и с общими показателями. При этом проводится структурная группировка – это разделение качественно однородной совокупности по какому-либо вариационному признаку. По росту, весу, уровню IQ, скорости движения, периоду полураспада и так далее. Признаков – тьма.
Да будет свет! – в качестве простейшего условного примера рассмотрим среднюю успеваемость студентов ВУЗа: 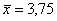
Гораздо интереснее провести типологическую группировку, например, разделить всех студентов на «физиков» и «лириков», и подсчитать групповые средние: 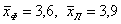
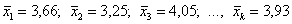
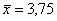
Довольно часто грань между типологической и структурной группировкой стирается. Приведу избитый, но показательный пример с банками. Все банки можно разделить на мелкие, средние и крупные (типологическая группировка). Но с другой стороны, эти категории основаны на количественном показателе, мелкие – меньше одного литра, средние – от одного до трёх, и крупные – больше трёх литров. То есть, это одновременно и структурная группировка.
Следует отметить, что при кажущейся простоте провести подобную группировку бывает не так-то просто. Трудность состоит в том, чтобы грамотно выделить различные категории (типы), и для этого, порой, исследуют целый комплекс показателей. Эксперты Центробанки гарантируют 🙂
Кроме того, существуют и другие виды группировок, в частности, аналитическая группировка и комбинационная группировка. Но о них позже, после практической разминки.
Ранее мы уже неоднократно проводили группировку данных, давайте вспомним пару примеров:
По результатам выборочного исследования рабочих цеха были установлены их квалификационные разряды: 4, 5, 6, 4, 4, 2, 3, 5, 4, 4, 5, 2, 3, 3, 4, 5, 5, 2, 3, 6, 5, 4, 6, 4, 3.
…
В этой задаче была проведена структурная группировка рабочих цеха по их разряду и получен дискретный вариационный ряд: 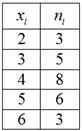
где 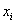
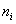
По результатам исследования цены некоторого товара в различных торговых точках города, получены следующие данные (в некоторых денежных единицах): 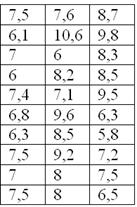
…
В этом примере мы тоже провели структурную группировку (товаров по их цене) и получили интервальный вариационный ряд: 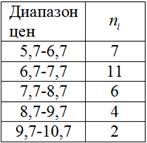
где 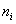
И сейчас мы продолжим группировать данные. Студентам чаще всего предлагают провести структурную и аналитическую группировку; разберём их по порядку. Затем потренируемся в комбинационной группировке, ну а группировку типологическую я оставлю за кадром, полагаю, разделить совокупность на кошек и собак ни у кого не вызовет трудностей.
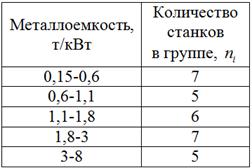
Суровая задача местного Политеха для студентов около- и машиностроительных специальностей:
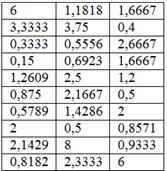
В результате выборочного исследования 30 станков рассчитаны их относительные показатели металлоёмкости (т/кВт):
а) вычислить общую среднюю;
б) выполнить структурную равноинтервальную группировку;
в) выполнить структурную равнонаполненную группировку;
г) выбрать наиболее удачную группировку и вычислить выборочные средние; результаты оформить в виде групповой таблицы;
д) по выбранной группировке построить интервальный вариационный ряд;
е) сделать выводы.
Но прежде немного о содержании. Согласно автору методички, относительная металлоемкость – это частное от деления веса станка на мощность его двигателя (тонн на киловатт). Разделили, например, 5 тонн на 2 кВт и получили 2,5 тонны на один кВт. Эти значения и представлены в таблице. Правильность и достоверность перечисленных фактов в который раз оставлю на совести автора, да и, в конце концов, нам требуется обработать числа, а уж что это такое – не особо важно, хоть объём талии пчёлок. …И всё-таки математика немного шизофреническая наука 🙂
Решение:
Ну, с пунктом а) справится даже неподготовленный человек. Очевидно, что для нахождения общей средней нужно просуммировать все значения и разделить полученный результат на объём выборки:
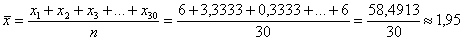
Эти и другие вычисления легко выполняются в Экселе, и чуть ниже будет ролик о том, как быстро выполнить все пункты задания. Ибо на калькуляторе щёлкать 30 слагаемых муторно (хотя, вариант вполне рабочий).
б) Выполним структурную равноинтервальную группировку. Пугаться не нужно, это задание уже было – нам нужно построить обычный интервальный вариационный ряд с равными интервалами, и я кратко повторю алгоритм.
В условии ничего не сказано о количестве интервалов, и поэтому для определения их оптимального количества используем формулу Стерджеса:
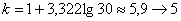
Найдём минимальное 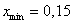
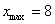
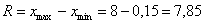
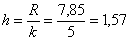
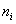
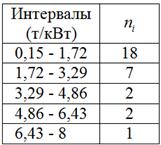
Контроль: 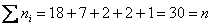
И уже сейчас мы видим, что построенный вариационный ряд не слишком хорош – по той причине, что в трёх последних интервалах слишком мало станков, и считать по ним средние значения и другие показатели не вполне корректно.
Во избежание этого недостатка используют разные методы, и один из них состоит в том, что использовать:
в) равнонаполненную группировку. Это разбиение совокупности на группы с одинаковым (или примерно одинаковым) количеством объектов, станков в данном случае. Но интервалы здесь получатся разной длины.
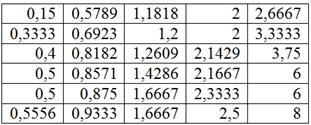
Отсортируем числа по возрастанию и выделим 5 групп по 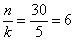
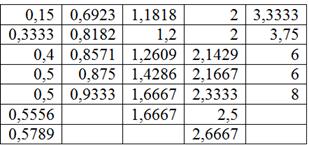
Формально всё выглядит тип-топ (и можно оставить так), но некоторые значения логичнее перенести в соседние группы. Так, значение 0,5789 (верхняя строка) явно ближе к 1-й группе, а значение 2,6667 – к предпоследней группе; туда их и перенесём:
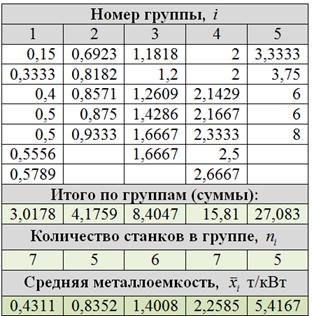
г) Очевидно, что равнонаполненная группировка более удачна, с ней и работаем. По каждой группе подсчитаем суммы, количество станков и выборочные средние. Результаты представим в виде групповой таблицы:
И на всякий пожарный примеры расчёта групповых средних:
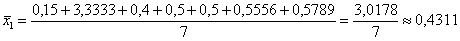
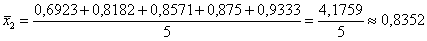
и так далее. Вычисления удобно проводить опять же в Экселе (см. ролик ниже).
Да, кстати, не забываем предварительно проконтролировать объём выборки: 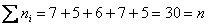
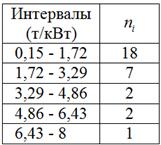
д) Построим интервальный вариационный ряд по равнонаполненной группировке. Границы интервалов можно брать как средние арифметические «стыковых» значений, например: 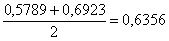
Полученный интервальный ряд имеет разную длину интервалов, но для него точно так же можно построить гистограмму, полигон и эмпирическую функцию распределения, а также рассчитать различные характеристики. Правда, с модой проблема будет и для её нахождения таки лучше использовать равноинтервальную группировку (пункт б).
Теперь смотрим ролик по быстрому и эффективному выполнению задания:

Выражаясь научно, мы выполнили статистическую сводку. Статистическая сводка – это комплекс действий по обработке статистических данных с целью анализа спастической совокупности. Причём, в пункте а) была простая статическая сводка (подсчёт общих показателей), которая переросла в сводку сложную, включающую в себя группировку данных, расчёт групповых характеристик и сведение результатов в групповую таблицу.
е) Я не случайно выделил этот пункт. Довольно часто в заданиях подобного типа требуется сделать краткие выводы – в них нужно отразить основные результаты выполненных действий и особенности исследуемой совокупности.
И мы сделаем простенькие выводы. Сказать здесь можно следующее. В результате исследования рассчитана средняя металлоёмкость 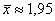
Несколько строчек вполне достаточно, даже многовато получилось.
Следующее задание для самостоятельного решения:
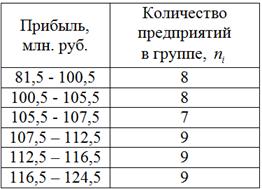
По результатам выборочного исследования 50 предприятий получены данные об их квартальной прибыли (числа в экселевском файле), млн. руб. Требуется: 1) вычислить среднюю прибыль, 2) провести равнонаполненную группировку и вычислить групповые средние, 3) построить соответствующий вариационный ряд, 4) сделать выводы.
Вообще, здесь удобно разбить выборку на 5 интервалов (и такой вариант вполне себе неплох), но от греха подальше лучше использовать формулу Стерджеса, что я и сделал в образце решения, который, как обычно, находится внизу страницы. Ваш вариант решения может немного отличаться от моей версии.
Теперь вернёмся к пункту «бэ» Примера 55, где была выполнена не слишком удачная равноинтервальная группировка, скопирую табличку сверху:
Как вы помните, от «куцых» интервалов мы избавились, выполнив равнонаполненную группировку. Но есть и другой метод «лечения», который называется перегруппировкой.
Перегруппировка – это вторичная группировка, которая состоит в преобразовании уже построенного вариационного ряда. И одним из инструментов перегруппировки является укрупнение интервалов. В данном случае можно просто объединить три последних интервала, и, коль скоро, нам известны первичные (исходные) данные, то заодно подкорректируем границы всех интервалов до удобных значений: 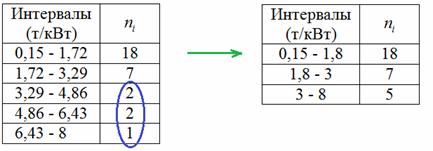
Не так, конечно, получилось подробно, как в равнонаполненной группировке, но тоже вполне наглядно. При желании, к слову, первый интервал легко измельчить, получив нечто близкое или даже совпадающее с этой группировкой. Благо, исходные числа в нашем распоряжении.
Но что делать, если первичные данные не известны?
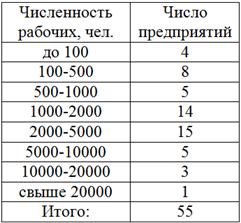
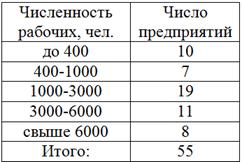
Перегруппируйте следующие данные о численности работающих на 55 предприятиях, образовав следующие группы: до 400, 400-1000, 1000-3000, 3000-6000, свыше 6000:
В этой задаче мы не знаем исходные варианты (конкретную численность рабочих по предприятиям), но решение есть! Для удобства оформлю его по пунктам, ВНИМАТЕЛЬНО вникайте в суть:
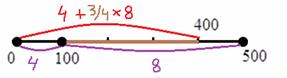
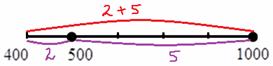
1) Выделим новый промежуток «до 400» (красный цвет на рисунке ниже). В него, понятно, войдёт интервал «до 100» (4 предприятия) и часть интервала «100-500», а именно часть 100-400, выделенная коричневым цветом:
Теперь длину коричневой части 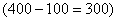
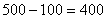
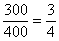
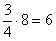
Итого в промежутке «до 400» оказывается 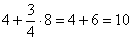
…вроде всё просто, а объяснить было довольно сложно 🙂 Соответственно, на кусок «400-500» останется 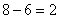
2) Выделим новый промежуток «400-1000». В него войдёт оставшийся старый «кусок» «400-500» с двумя предприятиями и старый интервал «500-1000» с 5 предприятиями:
Итого на промежутке «400-1000» оказалось 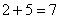
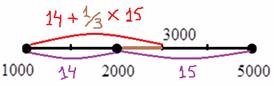
3) Выделим новый промежуток «1000-3000». В него полностью войдёт старый интервал «1000-2000» с 14 предприятиями и одна треть интервала с «2000-5000» с 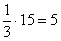
Нужную долю (одну треть) мы нашли как отношение длины коричневого интервала 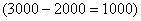
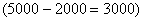
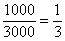
Таким образом, в промежуток «1000-3000» вошло 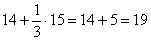
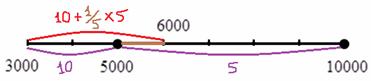
4) В новый промежуток «3000-6000» входят две трети старого интервала «2000-5000» (см. рис. выше), что составляет 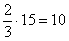
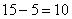
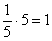
Одна пятая найдена как отношение длины коричневого интервала «5000-6000» к длине интервала «5000-10000»:
Таким образом, в промежуток «3000-6000» вошло 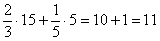
5) И, наконец, в последний новый промежуток «свыше 6000» входят четыре пятых старого интервала «5000-10000» (см. рис. выше) или 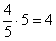
Итого: 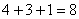
Перегруппировка завершена, новый вариационный ряд построен:
И обязательно проконтролируем объем выборки, мало ли что-то потерялось или мы где-то обсчитались: 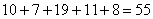
Следует отметить, что метод выделения долей, строго говоря, не точен, и если в нашем распоряжении есть первичные данные, то, конечно же, ориентируемся на них – в результате с высокой вероятностью получатся немного другие частоты по группам. Но для выборочной совокупности годится и долевая перегруппировка, поскольку от выборки к выборке мы всё равно будем получать разные значения и строить похожие, но всё же разные вариационные ряды.
Перегруппировка часто применятся для того чтобы сопоставить «родственные» совокупности с разными интервалами:
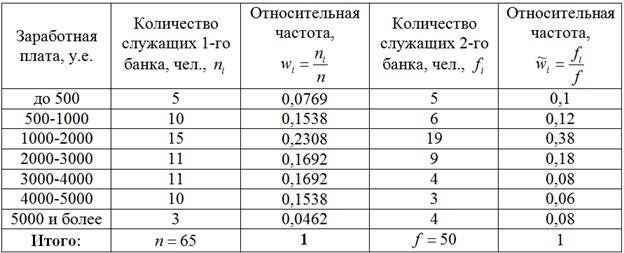
По результатам выборочного исследования двух банок банков получены данные о заработной плате их служащих: 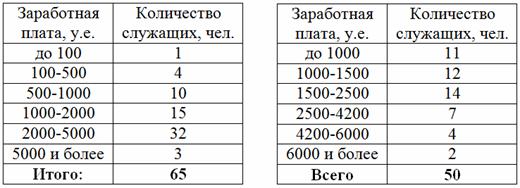
Сравнить уровень заработной платы банков, выделив интервалы: до 500, 500-1000,
1000-2000, 2000-3000, 3000-4000, 4000-5000, свыше 5000, и рассчитав относительные частоты по каждому банку. Результаты представить в виде общей таблицы, сделать выводы.
Для удобства я заготовил для вас Эксель-шаблон, не ленимся! Если трудно, то можно использовать рисунки с разметкой интервалов (по образцу предыдущего примера), в образце я ограничился аналитическим решением.
И я жду вас на следующем уроке, который посвящён дисперсиям, коль скоро, были средние, то где-то рядом нас поджидают и дисперсии.
Решения и ответы:
Пример 56. Решение:
1) вычислим среднюю квартальную прибыль предприятий:
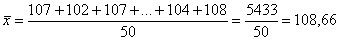
2) Проведём равнонаполненную группировку с равным или примерно равным количеством предприятий в каждой группе.
Оптимальное количество интервалов определим по формуле Стерджеса:
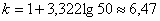
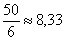
Упорядочим совокупность по возрастанию и выделим в ней следующие группы; в групповой таблице вычислим суммы и групповые средние: 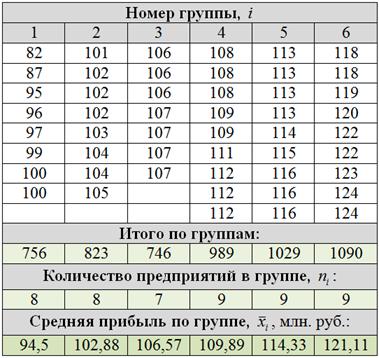
Промежуточный контроль: 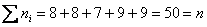
3) Построим интервальный вариационный ряд:
4) Средняя прибыль предприятий за квартал составила 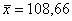
З.Ы. Возможно, вы заметили что-то ещё! 😉
Пример 58. Решение: 1) выполним перегруппировку по 1-му банку:
– В новый промежуток «до 500» войдут интервалы «до 100» и «100-500»:
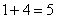
– Новые промежутки «500-1000, 1000-2000» совпадают со старыми интервалами.
– Новые промежутки «2000-3000, 3000-4000, 4000-5000» полностью входят в старый интервал «2000-5000». Делим частоту этого интервала на 3:
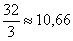
В промежутки «2000-3000, 3000-4000» относим по 11 человек, а в промежуток «4000-5000» – 10 человек (предполагая то, что людей с бОльшей заработной платой – меньше)
– Новый промежуток «5000 и более» совпадает со старым интервалом.
2) Выполним перегруппировку второго вариационного ряда:
– Старый интервал «до 1000» разобьём на два новых равных промежутка, при этом в промежуток «до 500» отнесём 5 человек, а в промежуток «500-1000» – 6 человек (предполагая, что людей с более низкой з/п – чуть меньше)
– В новый промежуток «1000-2000» входит интервал «1000-1500» и половина интервала «1500-2500», в людях это составит:
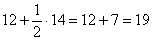
– В новый промежуток «2000-3000» входит половина интервала «1500-2500» и 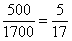
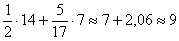
– В новый промежуток «3000-4000» входит 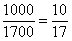
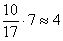
– В новый промежуток «4000-5000» входит 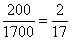
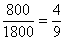
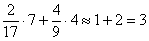
– И в новый промежуток «свыше 5000» входит 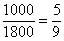
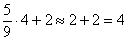
Результаты сведём в единую таблицу, при этом рассчитаем относительные частоты по каждому банку:
Краткие выводы: Для обоих банков характерна зарплата от 1000 до 2000 у.е., однако в 1-м банке чуть более высокий уровень заработной платы – значительное количество сотрудников получает более 2000 у.е. Но, скорее всего, основная их масса имеет з/п в диапазоне 2000-3000, здесь требуется дополнительное исследование первичных данных, поскольку формальное разбиение интервала «2000-5000» на три равных интервала не очень удачно.
З.Ы. Возможно, вы заметили что-то ещё! 😉
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5
Источник