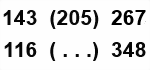Дидактическая игра по закреплению количества и счета «Пропущенное число»
марина
Дидактическая игра по закреплению количества и счета «Пропущенное число»
Дидактическая игра направлена на решение задач по фэмп. Ведущим видом деятельности в дошколном возрасте является- игра,поэтому обучение детей происходит непосредственно через игровую деятельность. Предлагаю вашему вниманию игру,которая предназначена для детей старшего дошкольного возраста.
Цель : упражнять детей в счете,найти пропущенное число.
Задачи : закрепление понятия «соседи числа«,уметь соотносить количество предметов с числом,развивать мышление и внимание.
Материал : карточки с изображением предметов от 1 до 10,набор карточек с изображением разного количества предметов
Данная игру можно использовать в непосредственно образовательной деятельности, в самостоятельной деятельности детей, так и в совместной деятельности воспитателя с детьми.
Ход игры
Ребенку дается карточка с изображением предметов справа и слева,в середине остается пустое место для карточки с правильным ответом. Затем ребенку предлагается посчитать количесвто предметов,соотнести с числом и определить какое же число пропущено в середине,также ребенку дается набор карточек с определенным количеством предметов для того чтобы он мог посчитать количество предметов и выбрать карточку с правильным ответом.
Дидактическая игра «Чем питаются животные» по закреплению знаний о том, чем питаются разные домашние и дикие животные Зайка завтракал на грядке, Как же овощи здесь сладки! Уплетал зайчишка ловко И капустку, и морковку. (Людмила Громова) Ежик по лесу гулял,.
Дидактическая игра «Накорми Китайца» для развития мелкой моторики, закрепления счета и цвета Предлагаю вашему вниманию авторскую дидактическую игру «Накорми Китайца» Назначение: предназначена для детей старшего дошкольного возраста.
Тренировка счета в пределах 10. Дидактическая игра «Пингвины» Дидактическая игра «Пингвины» Изготовлена для занятия по математике. Выполнена из бумаги и цветного картона. Цель игры: тренировка счета.
Дидактическая игра на определение количества звуков в словах «Построим пирамиду» Дидактическая игра «Построим пирамиду» Цель. Упражнять детей в определении количества звуков в словах. Игровой материал: 1. Рисунок пирамиды.
Дидактические игры на закрепление количества и счета Дидактические игры – Игры на закрепления количества и счета «ПРЯТКИ» Назвать цепочку чисел, пропуская несколько из них. Задача детей назвать.
Интеллектуальная игра по закреплению знаний о зимующих птицах «Что? Где? Когда?» Цель: Закреплять и расширять знания детей о зимующих птицах: об их внешнем виде, о питании, повадках. Задачи: -Учить отгадывать загадки.
Итоговое занятие по закреплению порядкового и количественного счета у детей ЦЕЛЬ: обобщение и закрепление полученных знаний ЗАДАЧИ: Образовательные: • Совершенствовать навыки счета у детей в пределах 10, закреплять.
Конспект урока математики в 1 классе по закреплению изученного материала «Прибавить и вычесть число 3» по УМК «Школа России» Цель: создать условия для закрепления знаний учащихся по теме : «Прибавить и вычесть число 3»; развивать навыки счета; совершенствовать.
Сценарий выпускного праздника в ДОУ для малого количества выпускников «В поисках волшебных пятерок» «В поисках волшебных пятерок» Сценарий выпускного праздника для малого количества выпускников Ход праздника: Праздник начинается с объявления.
Занятие по закреплению счета «Лесная школа» Воспитатель старшей группы МКДОУ «Детский сад № 12 г. Беслан» Атаева Людмила Геогриевна Виды детской деятельности: игровая, коммуникативная,.
Источник
Узнать ещё
Знание — сила. Познавательная информация
Вставить пропущенные числа
Вставить пропущенные числа в заданиях тестов iq может быть предложено в рисунках, где числа расположены в круге.
Как и в других заданиях из iq тестов, тест круги с цифрами требует установить числовую закономерность, связывающую данные цифры или числа. В числовой цепочке могут быть одна или сразу несколько закономерностей . IQ тесты с кругами могут задавать связь для чисел, стоящих рядом, либо через одно-два числа при движении по часовой стрелки или в обратном направлении, а также для чисел, стоящие напротив.
Рассмотрим конкретные примеры.
Вставить пропущенные числа.
Найти закономерность и заменить ? числами
1) В данном задании необходимо найти и вставить сразу два пропущенных числа. Эти неизвестные числа в круге находятся друг напротив друга, поэтому, скорее всего, они объединены некоторой закономерностью. С другой стороны, должна быть и другая закономерность, чтобы найти одно из чисел связки. Таким образом, будем искать две закономерности.
Ответ и решение скрыты под спойлером. Однако не торопитесь их прочесть, попробуйте найти неизвестные числа самостоятельно.
Каждое следующее число вверху между ?? получено увеличением на 3, а число напротив — увеличением в 3 раза.
Найти закономерность и заменить ? числами
2)В этом задании также неизвестны сразу два числа. Но они стоят в круге рядом, поэтому закономерность связывает, скорее всего, либо подряд идущие числа, либо числа через одно.
Две закономерности связывают числа через одно. В первой каждое следующее число увеличивается в 2 раза, во второй — в 5 раз.
Вставить пропущенные числа
3) Снова ищем сразу два числа. Неизвестные числа стоят рядом, поэтому закономерность может быть для чисел, идущих подряд. С другой стороны, числа стоят на окружности. Может быть зависимость не только между числами, стоящими рядом или через одно, но и между числами, стоящими друг напротив друга.
Начиная с верхней единицы по часовой стрелке через одно стоят квадраты натуральных чисел в порядке возрастания: 1,4,9,16. Начиная с 64 по часовой стрелке через одно стоят кубы натуральных чисел в порядке убывания: 64, 27, 8, 1.
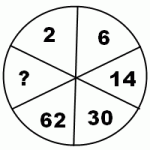
Вставить пропущенное число
4) Здесь неизвестное число всего одно. Соответственно, закономерность может связывать какие угодно числа: стоящие подряд, через одно, напротив друг друга или иная.
2·2+2=6. 6·2+2=14, 14·2+2=30, 30·2+2=62, 62·2+2=126.
Источник
Вставьте пропущенное число
Как правило, задания с числами в тестах IQ звучат так: «Вставьте пропущенное число» или «Вставьте пропущенные числа».
При схожести формулировки задачи могут существенно отличаться по уровню сложности и даже по оформлению. Как их решать?
Рассмотрим примеры числовых заданий из тестов на IQ.
1) Вставьте пропущенное число:
7; 12; 17; 22; ?
2) Найдите пропущенные числа:
3; 15; 5; 12; 7; 9; ? ?
3) Какое число пропущено?
4) Вставьте число, пропущенное в скобках:
5) Какие числа пропущены?
6) Найдите пропущенное число:
7) Определите, какое число пропущено:
8) Определить пропущенное число:
9) Найти пропущенное число:
10) Вставить пропущенное число:
Разумеется, вариантов заданий IQ тестов, в которых требуется вставить пропущенное число, намного больше.
Наша задача — при внешней непохожести IQ задач попытаться выработать системный подход к их решению.
Попробуйте определить пропущенные числа. Ответы и решения можно посмотреть под спойлером.
Каждое последующее число получаем прибавлением 5.
Числа, стоящие на нечетных местах, последовательно увеличиваем на 2.
Числа, стоящие на нечетных местах, последовательно уменьшаем на 3.
3∙2=6; 5∙2=10; следовательно, 9∙2=18.
Число в скобках — среднее арифметическое чисел вне скобок:
5) Вверху — 54, внизу — 16.
Числа в верхней строчке получаем последовательным умножением на 3, в нижней — последовательным делением на 2.
Чтобы получить числа 2-го столбца, числа первого столбца удваиваем и прибавляем числа третьего столбца:
4∙2+7=15; 10∙2+3=23; 9∙2+8=26.
Число в центре круга находим так: из суммы чисел, стоящих по вертикали, вычитаем сумму чисел по горизонтали:
Число в треугольнике в два раза больше суммы чисел вне треугольника:
Сумму чисел, стоящих у наклонных отрезков, делим на число, стоящее вверху вертикальной линии:
10) 180.
Числа второго круга в три раза меньше чисел первого круга:
18:3=6; 24:3=8; 60:3=20.
Числа третьего круга в три раза больше чисел первого круга:
18∙3=54; 24∙3=72; 60∙3=180.
Далее — поэтапное рассмотрение различных заданий с числами из тестов IQ.
Источник
Алгоритм нахождения пропущенного числа в выражениях в несколько действий. Начальная школа.
Методист Костанайского педагогического колледжа
Буртылева Зоя Александровна. 11.12.16.
Алгоритм нахождения пропущенного числа в начальной школе.
Мой педагогический стаж 35 лет. Из них 34 года я проработала учителем начальных классов. Педагогический опыт достаточно большой. За время работы мною найдены такие приёмы организации учебной деятельности, благодаря которым основные понятия программного материала как по русскому языку, так и по математике легко воспринимаются и усваиваются учащимися с различным уровнем обученности.
Совсем недавно я стала работать методистом по практике в Костанайском педагогическом колледже. Достаточно часто во время подготовки и проведении зачётных уроков, я сталкиваюсь с тем, что студенты нацеливают свою работу только на то, чтобы выполнить задание — решить задачу, уравнение, найти значение выражения; просклонять имя существительное, разобрать слово по составу и т. д. Но не понимают, что очень важно научить детей анализировать задание и найти способ его выполнения. А как это важно!
И сегодня мне хочется поделиться своими находками с будущими выпускниками педагогического колледжа и молодыми учителями начальной школы, не имеющими большого опыта. Быть может кто-то уже использует эти находки в своей работе, тогда я буду рада пообщаться со своими единомышленниками.
Итак, достаточно часто в учебники по математике включают задания со звёздочкой вида:
. — 5 = 4, . + 4 = 9, 9 — . = 6.
Подобные задания основываются на знании состава чисел и, казалось бы, сильных затруднений не вызывают у учащихся. Мы рассуждаем следующим образом:
От какого числа нужно отнять 5, чтобы получилось 4?
Ребята вспоминают состав числа 9. 9 — это 5 и 4.
От 9 отнимаем 5, остаётся 4.
Значит пропущенное число — 4.
Но вот задания усложняются и появляются задания вида:
10 — . + 3 + 4 — 6 +5 = 7
Как быть ученику? Подбирать до бесконечности, пока не подойдёт одно из чисел?
Задумываясь над подобным заданием, для себя я установила некую связь между предыдущими и последующим действиями.
Я предлагаю вникнуть в процесс анализа следующего выражения: 10 — . + 3= 4. Начнем с последнего действия.
То, что закрашено красным цветом, закрываем и представляем как один компонент — неизвестное число (неизвестный компонент -слагаемое). Задаём детям вопрос: к какому числу (слагаемому) нужно +3, чтобы стало 4? Конечно же к 1 (выделим жёлтым цветом). Значит в той части, которая закрашена красным цветом ( 10-. ) должно в результате получится 1 .
10-. =1 Нужно от 10 отнять 9, чтобы получилось число 1. Вот и пришли к искомому числу.
Проверим — 10 — 9 + 3= 4. Всё верно.
Рассмотрим более сложное выражение: 10 — . + 3 + 4 — 6 +5 = 7
Анализ и рассуждение начнём снова с конца.
10 — … + 3 + 4 – 6 + 5 = 7
Снова закрываем всю запись до последнего действия. Рассуждаем так: к какому числу нужно прибавить 5, чтобы получилось 7? Отвечаем: к 2.
Надписываем над предпоследним действием число 2.
10 — … + 3 + 4 – 6 + 5 = 7
Продвигаемся в своём рассуждении дальше.
10 — … + 3 + 4 – 6 + 5 = 7
Что закрашено красным цветом- неизвестное число (или неизвестное уменьшаемое). От какого числа нужно отнять 6, чтобы получилось 2? От 8. Надписываем над предпоследним действием.
10 — … + 3 + 4 – 6 + 5 = 7
К какому числу (слагаемому) нужно прибавить 4, чтобы получилось 8? К 4.
Надписываем над предпоследним действием 4. (выделено жёлтым цветом)
Идём дальше. К какому числу нужно прибавить 3, чтобы в ответе получилось 4? К 1. Значит над первым действием надписываем число 1 (выделено жёлтым цветом).
Вот и завершающий этап. Сколько нужно отнять от 10, чтобы получить 1? Конечно же 9. Вставляем в пустую клетку число 9.
И проверяем всё выражение.
10 – 9 + 3 + 4 – 6 + 5 = 7
Пропущенное число найдено. Так можно вести рассуждение с любыми числами — от однозначного до многозначных. Попробуйте. Действует.
1123095 — . + 347820 — 56208 + 3456= 935501
У меня получился ответ: 182662
Подводя итог, мне хочется сказать, учите детей рассуждать и устанавливать связи и ваши ученики порадуют вас новыми успехами и открытиями. Удачи!
Источник
