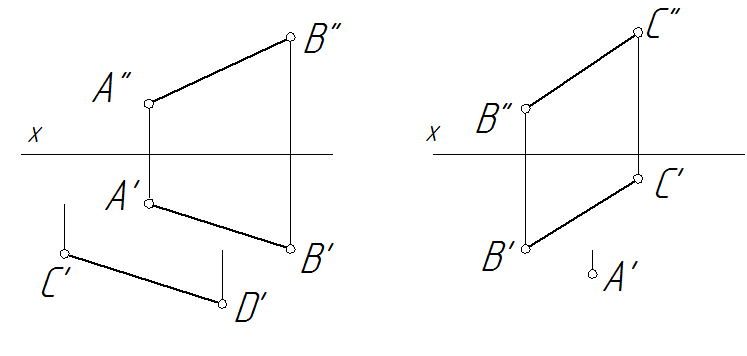
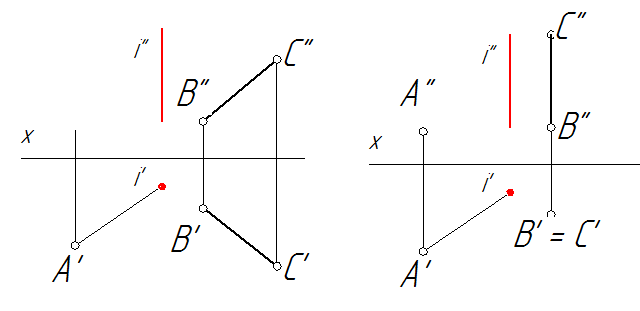
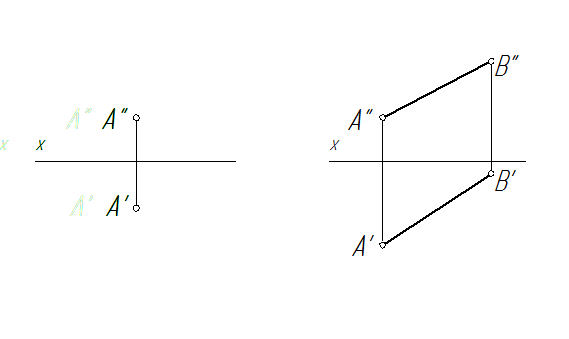Способы вращения вокруг оси параллельной плоскости проекций
Контрольные задания по теме: Рабочая тетрадь задача 50
Трудоемкость и точность графического решения задач часто зависит не только от сложности задач, но и от того, какое положение занимают геометрические фигуры по отношению к плоскостям проекций. Наиболее выгодными являются положения, параллельные плоскостям проекций или перпендикулярные им.
Переход от общего положения геометрической фигуры к частному можно осуществить двумя путями:
а) перемещением в пространстве проецируемой фигуры так, чтобы она заняла частное положение относительно плоскостей проекций, которые при этом не меняют своего положения;
б) выбором новой плоскости проекций, по отношению к которой фигура, не имеющая своего положения в пространстве, окажется в частном положении. Первый путь лежит в основе способа плоскопараллельного перемещения, а второй — в основе способа замены плоскостей проекций.
Существует несколько способов плоскопараллельного перемещения:
1. Способ параллельного перемещения. При этом плоскости, по которым двигаются точки фигуры, параллельны плоскости проекций. Траектория — произвольная плоская линия;
2. Способ вращения вокруг оси, перпендикулярной к плоскости проекций. Траектории перемещаемых точек — дуги окружностей, центры которых находятся на оси вращения;
3. Способ вращения вокруг оси параллельной плоскости проекций (вокруг линии уровня).
Это частный случай параллельного перемещения. За траекторию движения точки принимается не произвольная линия, а дуга окружности, центр которой находится на оси вращения, а радиус равен расстоянию между осью вращения и данной точкой.
При вращении точки вокруг оси перпендикулярной, П 2 , фронтальная проекция точки перемещается по окружности, а горизонтальная — по прямой, перпендикулярной оси вращения. Если же точка вращается вокруг оси, перпендикулярной П 1 , то в горизонтальной плоскости траекторией ее движения будет окружность, а во фронтальной – прямая, перпендикулярная оси вращения. На рисунке 32 показано построение новых проекций точек при помощи способа вращения. На рисунке 32 а – вращение вокруг фронтально-проецирующей оси, на рисунке 32 б – вокруг горизонтально-проецирующей оси.
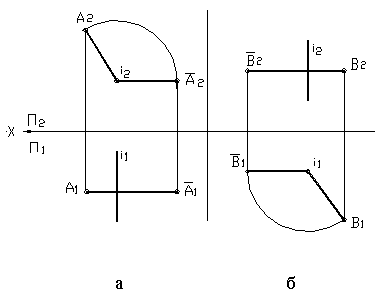
Рисунок 32
Этим способом удобно находить натуральные величины отрезков и фигур, занимающих проецирующее положение.
На рисунке 33 показан пример определения натуральной величины треугольника АВС, плоскость которого перпендикулярна П 2 . За ось вращения необходимо взять фронтально-проецирующую прямую, проходящую через точку, принадлежащую этой плоскости. В данном случае выбрана точка А — вершина треугольника. Плоскость треугольника вращается во фронтальной плоскости вокруг оси до положения, параллельного горизонтальной плоскости. Во фронтальной плоскости точки С и В перемещаются по окружностям, радиус которых равен расстоянию от оси вращения до фронтальных проекций точек. В горизонтальной плоскости траектории движения точек – прямые, перпендикулярные оси. Полученная проекция треугольника А´В´С´, является его натуральной величиной.
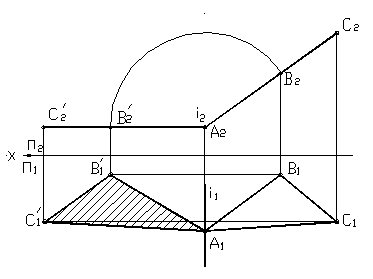
Рисунок 33
Способ вращения наиболее часто применяется при определении натуральных величин сечений поверхностей плоскостями частного положения.
Сущность этого способа состоит в том, что положение фигуры в пространстве не меняется, а вводится новая система плоскостей проекций. Новая плоскость проекции выбирается перпендикулярно к одной из старых. При этом, проецируемая фигура по отношению к новой плоскости занимает частное положение, обеспечивая наиболее удобное решение задачи. Если замена одной плоскости не обеспечивает требуемый результат, то новую плоскость заменяют еще раз.
На рисунке 34 показано построение проекции точки А в новой системе плоскостей проекций при замене плоскости П 1 на П 4 . Плоскость П 4 перпендикулярна П 2 . Проекция точки А1 заменяется на А 4 . По линии связи откладывается расстояние от заменяемой проекции точки до новой оси.
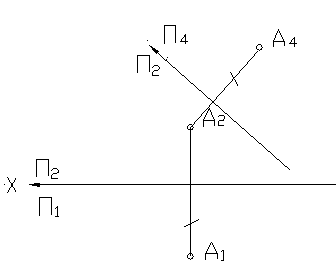
Рисунок 34
На рисунке 35 дан пример определения натуральной величины отрезка общего положения. Новая плоскость П 4 выбирается параллельно одной из проекций отрезка. При этом проекция отрезка на эту плоскость будет являться его натуральной величиной.
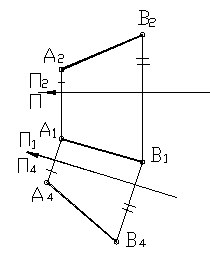
Рисунок 35
В некоторых случаях требуется замена двух плоскостей проекции. Например, при определении расстояния от точки до прямой. При этом прямую необходимо спроецировать в точку. На рисунке 36 отрезок общего положения переведен в проецирующее положение по отношению к плоскости П5.
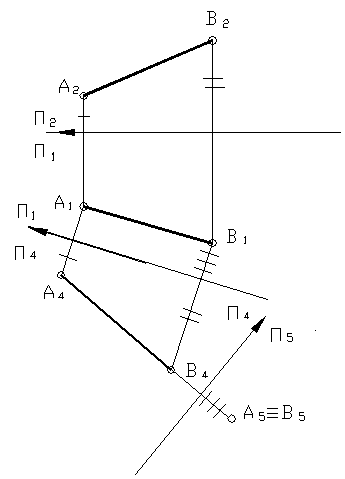
Рисунок 36
1. Назовите, какие вы знаете способы преобразования чертежа. Для чего они применяются?
2. Какие задачи можно решать при помощи способа вращения вокруг проецирующей оси?
3. По каким линиям перемещаются проекции точки при вращении вокруг горизонтально проецирующей оси?
4. Можно ли определить натуральную величину фигуры общего положения способом вращения вокруг проецирующей оси?
5. В чем суть способа замены плоскостей проекций?
6. Как построить проекцию точки в новой системе плоскостей проекций? Этапы построения.
7. Сколько замен нужно осуществить, чтобы перевести отрезок общего положения в проецирующее положение?
8. Как нужно выбрать новую плоскость, для того, чтобы сделать плоскость общего положения проецирующей?
© ФГБОУ ВПО Красноярский государственный аграрный университет
Источник
Способ вращения вокруг оси, параллельной плоскости проекций.
Способ вращения вокруг оси, параллельной плоскости проекций особенно широко применяется при решении четвертой задачи на преобразование чертежа, т.е. при преобразовании плоскости общего положения в плоскость уровня. При таком преобразовании все фигуры, лежащие в плоскости, будут проецироваться в натуральную величину. Особое преимущество настоящего способа преобразования перед ранее рассмотренными, состоит в том, что он наиболее рационален, т.к. этот способ переводит плоскость общего положения в плоскость уровня, минуя предварительный ее перевод в плоскость проецирующую, что было необходимо во всех предыдущих способах.
По этой причине задачи на определение истинных величин фигур и углов решаются преимущественно этим, способом.
Вращением около горизонтали, т. е. прямой, параллельной плоскости p1, найдем натуральную величину основания пирамиды — треугольника АВС.
1.Построив в плоскости треугольника горизонталь h(C1), принимаем ее за ось вращения.
Горизонтальные проекции окружностей, по которым будут перемещаться вершины А и В представляют собой прямые, перпендикулярные к оси вращения.(рис.12.1)
2.Находим повернутое положение вершин треугольника.
Новое положение вершины В — точку В1 / , предварительно найдя способом прямоугольного треугольника натуральное значение радиуса вращения этой точки,
R = ОВ = O / В о.(рис.12.2)
Вершина треугольника С, как лежащая на оси вращения, останется неподвижной.
Повернутое положение вершины А найдем из двух следующих условий.
а)Горизонтальная проекция окружности, как отмечалось выше, по которой будет перемещаться вершина А, представляет собой прямую, перпендикулярную к оси вращения.
б) Сторона AB в повернутом положении, как и до поворота, будет проходить через точку 1. Точка 1 в процессе поворота остается неподвижной, т.к. она лежит на оси вращения. Проводим прямую через точки В ′ 1, 1 ′ .
Пересечение прямых, найденных из этих двух условий, дает нам новую горизонтальную проекцию повернутой вершины А — точку А ′ 1.(рис.12.3)
Соединяя вершины А ′ 1,В ′ 1,C ′ получаем новую горизонтальную проекцию треугольника АBС, плоскость которого параллельна плоскости p1 . Следовательно треугольник А ′ 1 В ′ 1C ′ представляет собой натуральную величину заданного треугольника:
[DA1 / B1 / C / ] 
Задача №4. Определить истинную величину ребра SC (в мм) и уголего наклона к плоскости основания пирамиды (в градусах).
Источник
Способ вращения вокруг оси, параллельной плоскости проекций.
Способ вращения вокруг оси, параллельной плоскости проекций особенно широко применяется при решении четвертой задачи на преобразование чертежа, т.е. при преобразовании плоскости общего положения в плоскость уровня. При таком преобразовании все фигуры, лежащие в плоскости, будут проецироваться в натуральную величину. Особое преимущество настоящего способа преобразования перед ранее рассмотренными, состоит в том, что он наиболее рационален, т.к. этот способ переводит плоскость общего положения в плоскость уровня, минуя предварительный ее перевод в плоскость проецирующую, что было необходимо во всех предыдущих способах.
По этой причине задачи на определение истинных величин фигур и углов решаются преимущественно этим, способом.
Вращением около горизонтали, т. е. прямой, параллельной плоскости p1, найдем натуральную величину основания пирамиды — треугольника АВС.
1.Построив в плоскости треугольника горизонталь h(C1), принимаем ее за ось вращения.
Горизонтальные проекции окружностей, по которым будут перемещаться вершины А и В представляют собой прямые, перпендикулярные к оси вращения.(рис.12.1)
2.Находим повернутое положение вершин треугольника.
Новое положение вершины В — точку В1 / , предварительно найдя способом прямоугольного треугольника натуральное значение радиуса вращения этой точки,
R = ОВ = O / В о.(рис.12.2)
Вершина треугольника С, как лежащая на оси вращения, останется неподвижной.
Повернутое положение вершины А найдем из двух следующих условий.
а)Горизонтальная проекция окружности, как отмечалось выше, по которой будет перемещаться вершина А, представляет собой прямую, перпендикулярную к оси вращения.
б) Сторона AB в повернутом положении, как и до поворота, будет проходить через точку 1. Точка 1 в процессе поворота остается неподвижной, т.к. она лежит на оси вращения. Проводим прямую через точки В ′ 1, 1 ′ .
Пересечение прямых, найденных из этих двух условий, дает нам новую горизонтальную проекцию повернутой вершины А — точку А ′ 1.(рис.12.3)
Соединяя вершины А ′ 1,В ′ 1,C ′ получаем новую горизонтальную проекцию треугольника АBС, плоскость которого параллельна плоскости p1 . Следовательно треугольник А ′ 1 В ′ 1C ′ представляет собой натуральную величину заданного треугольника:
[DA1 / B1 / C / ] 
Задача №4. Определить истинную величину ребра SC (в мм) и уголего наклона к плоскости основания пирамиды (в градусах).
Способ вращения вокруг оси, перпендикулярной к плоскости проекций.
Это преобразование является частным случаем способа плоскопараллельногоперемещения.
Повернем реберo пирамиды вокруг проецирующей оси i, проходящей через вершину S, до положения, параллельного плоскости проекций. Тогда на эту плоскость ребро спроецируется без искажения. Одновременно определится и угол его наклона к основанию пирамиды.
1. Перемещаем треугольник АВС параллельно одной из плоскостей проекций так, чтобы после преобразования он занял проецирующее положение (см. задачу №1).
2.Располагаем вырожденную фронтальную проекцию DA2B2C2 –отрезок [A2 // B2 // C2 // ]параллельно оси х:
При этом не изменится величина его фронтальной проекции:
[A2 // B2 // C2 // ] 
Горизонтальные проекции точек перемещаются в новое положение по прямым параллельным оси х. По линиям связи строим горизонтальную проекцию DA2B2C2 (ΔA2 / B2 C2 / ), которая конгруэнтна основанию пирамиды: [DA2 / B2 / C2 / ] 
3.Перемещаем вершину пирамиды из положения S1 в положение S2. Строим проекции ребра SC: [S2 // C2 // ] 
4. Через вершину С2 пирамиды проводим ось вращения, перпендикулярную пл. p1: i2 
3. Повернем ребро [S2 C2] вокруг этой оси до положения, параллельного пл.p2: [S3 C2]// p2
На чертеже его горизонтальную проекцию располагаем параллельно оси х, т.е. [S / 3 C / 2]// х;
На фронтальную плоскость проекции p2 ребро [S3 C2] и угол его наклона к основанию пирамиды проецируется без искажения (рис.13).
Измеряем величину искомых параметров и указываем их на чертеже.
Варианты заданий
| Номер варианта | Координаты точек | ||||||||||
| S | A | B | C | ||||||||
| X | Y | Z | X | Y | Z | X | Y | Z | X | Y | Z |
Рис. 14 Компоновка и исполнение листов.
Обозначения и символы
Обозначения геометрических фигур
| Обозначения | Содержание |
| А,В,…,1,2,… | Точки |
| a,b,… l, m,… | Линии, произвольно расположены в пространстве |
| h f | Линии уровня: горизонталь фронталь |
| [AB] | Отрезок прямой, ограниченной точками А и В |
 | Поверхности (в том числе плоскости) |
 ABC ABC  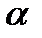 | Угол с вершинной в точке В |
ABC  … … | Угловая величина (градусная мера) угла АВС, угла 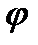 |
| Обозначения прямого угла | |
   | Расстояние между геометрическими фигурами: между точками А и В между точкой А и поверхностью 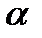 между линиями a и b между линиями a и b |
| p1 | горизонтальная плоскость проекции |
| p2 | фронтальная плоскость проекции |
| p3, p4,… | Профильная и другие дополнительные плоскости проекций |
| x,y,z | Оси проекций: x-ось абсцисс, y-ось ординат, z-ось аппликат |
| A / ,B / ,…,1 / ,2 / ,… A // ,B // ,…1 // ,2 // | Проекции точек: горизонтальные фронтальные |
| a / ,b / ,…,l / , a // b // …,l // ,… | Проекции линий: горизонтальные фронтальные |
  | Проекции поверхностей (в том числе плоскостей): горизонтальные фронтальные |
| hоa foa | Следы плоскостей (поверхностей): горизонтальные фронтальные |
| aπ1, bπ1, ….. aπ2, bπ2, ….. | Следы прямых линий: горизонтальные фронтальные |
Символы, обозначающие отношения между геометрическими фигурами.
| Обозначение | Содержание | Пример записи |
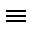 | тождественны |  |
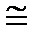 | конгруэнтны |  |
 | подобны |  |
 | параллельны | a // b |
 | перпендикулярны | a  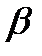 |
 | скрещиваются | C  b b |
 | касательные | t   |
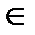 | принадлежит, является элементом | A 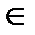 a a |
 | включает, содержит | b  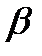 |
 | объединение | A  B=[AB] B=[AB] |
| ∩ | пересечение | M=L∩  |
 | эквивалентность | A 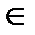 L L  a a  A A 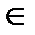 a a |
 | логическое следствие |   a a    m m  a a |
| ^ | Знак, соответствующий союзу «и» | (h  a)^(h//p1) a)^(h//p1) |
Задачи для самостоятельного решения.
1.Определить расстояние от произвольной точки А, принадлежащей плоскости π1 до прямой ВС, лежащей в плоскости π2 .
2.Вращением вокруг заданной оси совместить точку А с плоскостью α (рис.15).
3.Определить угол между произвольными отрезками АВ и СD (рис.16).
4. В плоскости треугольника АВС провести прямую, параллельную стороне АВ и на расстоянии 10мм от последней (рис. 17).
5.Определить угол между осью х и прямой АВ (рис.18).
6.Найти геометрическое место точек, равноудаленных от сторон угла АВС (рис19).
7.Дана прямая АВ и горизонтальная проекция прямой CD. Построить фронтальную проекцию прямой CD , если известно, что прямые параллельны и расстояние между ними равно 15мм (рис.20).
8.Дана прямая ВС и горизонтальная проекция точки А. Определить недостающую проекцию точки А, если известно, что расстояние от точки до прямой равно 20мм (рис.21).
9.Определить фронтальную проекцию точки А, зная, что при вращении около заданной оси точка окажется на прямой ВС (рис.22).
10.Повернуть точку А вокруг заданной оси так, чтобы в новом положении она оказалась на расстоянии 25мм от прямой ВС (рис.23).
11.Повернуть прямую АВ вокруг оси, перпендикулярной к плоскости проекций π1 так, чтобы в новом положении она прошла через заданную точку С (рис.24).
12.Способом вращения определить истинную величину шестиугольника ABCDEF (рис.25).
13.Заменить плоскость π2 так, чтобы точка А была удалена от новой плоскости π4 на 30мм (рис.26).
14. Заменить одну из плоскостей так, чтобы в новой системе плоскостей отрезок стал фронталью (рис.27).
Вопросы для самопроверки.
1. Сформулируйте условия принадлежности прямой и точки к плоскости. Запишите эти условия с помощью символов.
2. Какие линии плоскости называются главными? Укажите характерные особенности проекций этих линий на эпюре Монжа.
3. Сформулируйте условия перпендикулярности прямой и плоскости.
4. Как направляются на чертеже проекции прямой, перпендикулярной к плоскости?
5. Как проецируется прямой угол, одна сторона которого параллельна плоскости проекций, а другая ей перпендикулярна?
6. Как используется свойство проекций прямого угла при построении на чертеже прямой, перпендикулярной к плоскости?
7. Какие плоскости называются проецирующими? В чем состоит отличительная особенность их ортогональных проекций?
8. Как изображают на чертеже фронтально — или горизонтально-проецирующую плоскость, проведенную через прямую общего положения?
9. Как найти точку встречи прямой с плоскостью, когда они занимают общее положение? Запишите символически алгоритмы решения этой задачи.
10.Как определить натуральную величину отрезка прямой общего положения?
11.Сформулируйте условие параллельности двух плоскостей: прямой и плоскости.
12.Как построить плоскость, перпендикулярную к заданной прямой?
13.Как построить линию пересечения двух плоскостей общего положения? Запишите символически алгоритм решения этой задачи.
14.В чем состоит метод конкурирующих точек для определения видимости на эпюре?
15.Сформулируйте условие перпендикулярности двух плоскостей.
16.Какова цель преобразования чертежа?
17.Какие способы преобразования чертежа Вам известны?
18.В чем принципиальное различие рассмотренных способов преобразования чертежа?
19.Назовите основные задачи, решаемые преобразованием чертежа.
20.Назовите метрические задачи, решаемые одним преобразованием.
21. Назовите метрические задачи для решения которых требуется два преобразования. Какова последовательность их выполнения?
22.Назовите основные свойства преобразования чертежа способом плоскопараллельного перемещения.
23.Назовите закономерности преобразования чертежа способом вращения вокруг проецирующей прямой.
24.В чем разница способа вращения вокруг проецирующей прямой и плоскопараллельного перемещения?
25.В каких случаях удобно применять способ вращения вокруг линии уровня?
1. Фролов С.А. Начертательная геометрия. М.: «Машиностроение»,1983.
2. Фролов С.А. Сборник задач по начертательной геометрии. М.: «Машиностроение», 1980.
3. Гордон В.О., Семенов — Огиевский М.А. Курс начертательной геометрии. М.: Высш. шк.,2002.
4. Гордон В.О., Иванов Ю.Б., Солнцева Т.Е. Сборник задач по курсу начертательной геометрии. М.: Высш. шк., 2000.
Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Источник