Способы увеличения константы скорости уравнение аррениуса
ФИЗИЧЕСКАЯ И КОЛЛОИДНАЯ ХИМИЯ
Конспект лекций для студентов биофака ЮФУ (РГУ)
2.1 СКОРОСТЬ ХИМИЧЕСКОЙ РЕАКЦИИ
2.1.9 Влияние температуры на константу скорости реакции
Константа скорости реакции есть функция от температуры; повышение температуры, как правило, увеличивает константу скорости. Первая попытка учесть влияние температуры была сделана Я. Г. Вант-Гоффом, который сформулировал следующее эмпирическое правило:
При повышении температуры на каждые 10 градусов константа скорости элементарной химической реакции увеличивается в 2 – 4 раза.
Величина, показывающая, во сколько раз увеличивается константа скорости при повышении температуры на 10 градусов, есть температурный коэффициент константы скорости реакции γ . Математически правило Вант-Гоффа можно записать следующим образом:
(II.29)
(II.30)
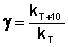
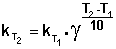
Однако правило Вант-Гоффа применимо лишь в узком температурном интервале, поскольку температурный коэффициент скорости реакции γ сам является функцией от температуры; при очень высоких и очень низких температурах γ становится равным единице (т.е. скорость химической реакции перестает зависеть от температуры).
2.1.10 Уравнение Аррениуса
Очевидно, что взаимодействие частиц осуществляется при их столкновениях; однако число столкновений молекул очень велико и, если бы каждое столкновение приводило к химическому взаимодействию частиц, все реакции протекали бы практически мгновенно. С. Аррениус постулировал, что столкновения молекул будут эффективны (т.е. будут приводить к реакции) только в том случае, если сталкивающиеся молекулы обладают некоторым запасом энергии – энергией активации.
Энергия активации есть минимальная энергия, которой должны обладать молекулы, чтобы их столкновение могло привести к химическому взаимодействию.
Рассмотрим путь некоторой элементарной реакции
Поскольку химическое взаимодействие частиц связано с разрывом старых химических связей и образованием новых, считается, что всякая элементарная реакция проходит через образование некоторого неустойчивого промежуточного соединения, называемого активированным комплексом:
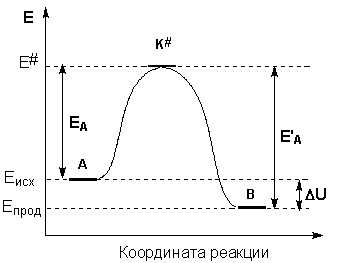
Образование активированного комплекса всегда требует затраты некоторого количества энергии, что вызвано, во-первых, отталкиванием электронных оболочек и атомных ядер при сближении частиц и, во-вторых, необходимостью построения определенной пространственной конфигурации атомов в активированном комплексе и перераспределения электронной плотности. Таким образом, по пути из начального состояния в конечное система должна преодолеть своего рода энергетический барьер. Энергия активации реакции приближённо равна превышению средней энергии активированного комплекса над средним уровнем энергии реагентов. Очевидно, что если прямая реакция является экзотермической, то энергия активации обратной реакции Е’А выше, нежели энергия активации прямой реакции EA. Энергии активации прямой и обратной реакции связаны друг с другом через изменение внутренней энергии в ходе реакции. Вышесказанное можно проиллюстрировать с помощью энергетической диаграммы химической реакции (рис. 2.5).
Рис. 2.5 Энергетическая диаграмма химической реакции.
Eисх – средняя энергия частиц исходных веществ,
Eпрод – средняя энергия частиц продуктов реакции
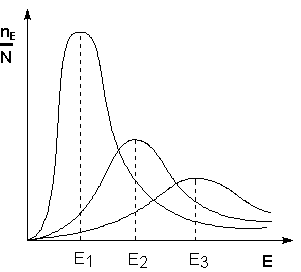
Поскольку температура есть мера средней кинетической энергии частиц, повышение температуры приводит к увеличению доли частиц, энергия которых равна или больше энергии активации, что приводит к увеличению константы скорости реакции (рис.2.6):
Рис. 2.6 Распределение частиц по энергии
Здесь nЕ/N – доля частиц, обладающих энергией E;
Ei — средняя энергия частиц при температуре Ti (T1 уравнения Аррениуса . Согласно уравнению изобары Вант-Гоффа,
(II.31)
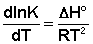
Поскольку константа равновесия есть отношение констант скоростей прямой и обратной реакции, можно переписать выражение (II.31) следующим образом:
(II.32)
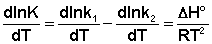
Представив изменение энтальпии реакции ΔHº в виде разности двух величин E1 и E2, получаем:
(II.33)
(II.34)
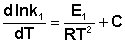
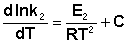
Здесь С – некоторая константа. Постулировав, что С = 0, получаем уравнение Аррениуса, где EA – энергия активации :
(II.35)
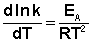
После неопределенного интегрирования выражения (II.35) получим уравнение Аррениуса в интегральной форме:
(II.36)
(II.37)
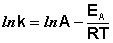
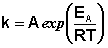
Рис. 2.7 Зависимость логарифма константы скорости химической
реакции от обратной температуры.
Здесь A – постоянная интегрирования. Из уравнения (II.37) нетрудно показать физический смысл предэкспоненциального множителя A, который равен константе скорости реакции при температуре, стремящейся к бесконечности. Как видно из выражения (II.36), логарифм константы скорости линейно зависит от обратной температуры (рис.2.7); величину энергии активации EA и логарифм предэкспоненциального множителя A можно определить графически (тангенс угла наклона прямой к оси абсцисс и отрезок, отсекаемый прямой на оси ординат).
(II.38)
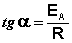
Зная энергию активации реакции и константу скорости при какой-либо температуре T1, по уравнению Аррениуса можно рассчитать величину константы скорости при любой температуре T2:
(II.39)
Copyright © С. И. Левченков, 1996 — 2005.
Источник
Уравнение Аррениуса
В 1889 г. шведский ученый Сванте Аррениус на основании экспериментов вывел уравнение, которое названо его именем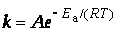 
где k – константа скорости реакции; А – предэкспоненциальный множитель; е – основание натурального логарифма; Еа – постоянная, называемая энергией активации, определяемая природой реакции. Значения Еа для химических реакций лежат в пределах 40 – 400 кДж/ моль.
После логарифмирования уравнение имеет вид
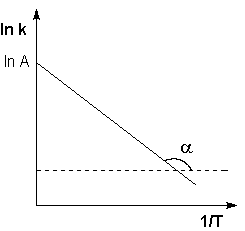
Если представить графическую зависимость lnk = f(1/T), то она имеет вид (рис 17).
Здесь tgα = -Еа/R и Еа = — Rtgα. Отрезок, отсекаемый на оси ординат равен lnА.
Итак, константа скорости реакции (и скорость) возрастает с увеличением температуры по экспоненциальному закону. В соответствии с уравнением Аррениуса константа скорости реакции уменьшается с ростом энергии активации. Уравнение Аррениуса позволяет рассчитывать константы скорости (и скорости) при различных температурах.
Энергия активации
Аррениус предположил, что реагировать между собой могут только те молекулы, которые находятся в активной форме, образующиеся из обычных молекул. Такие молекулы были названы активными, а энергия, необходимая для перевода обычных молекул в активное состояние, энергией активации.
В самом деле, в ходе химической реакции разрушаются одни и возникают другие молекулы, происходит изменение химических связей, т.е. перераспределение электронной плотности. Если бы старые связи в ходе реакции сразу полностью разрушались, то на это потребовалось бы большое количество энергии, и реакция протекала крайне медленно. Как показали исследования, в ходе реакции система проходит через переходное состояние, через образование активированного комплекса. Например, ход реакции
АВ + DC = AD + BC В активированном комплексе старые связи еще не разорваны, но уже ослаблены, новые связи наметились, но еще не образовались. Время существования его не велико (10‾ 14 – 10‾ 11 с). При распаде комплекса образуются либо продукты реакции, либо исходные вещества. Для образования переходного комплекса необходима энергия. Система в переходном состоянии имеет более высокую энергию, чем в исходном и конечном состояниях. Энергия, необходимая для перехода вещества в состояние активированного комплекса, называется энергией активации. Образование активированного комплекса определяется энергией молекул. Молекула, энергия которой достаточна для образования активированного комплекса, называется активной. Доля таких молекул зависит от температуры. При высоких температурах доля активных молекул, энергия которых равна или выше энергии активации, велика и, соответственно, растет доля молекул способных к активным столкновениям с образованием активированного комплекса, т.е. реакции идут быстро. Чем выше энергия активации, тем меньше доля частиц, способных к активному взаимодействию. Экзотермические реакции протекают с меньшей энергией активации, чем эндотермические (рис.18). Высокая энергия активации (высокий энергетический барьер) является причиной того, что многие химические реакции при невысоких температурах не протекают, хотя термодинамически возможны (ΔG
Дата добавления: 2016-01-16 ; просмотров: 1049 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник
Калькулятор уравнения Аррениуса
(Единицы для постоянной Аррениуса и константы скорости одинаковы и зависят от скорости реакции. )
Что такое уравнение Аррениуса?
Уравнение Аррениуса — это формула, которая описывает, как скорость реакции изменяется в зависимости от температуры или константы скорости. Если мы посмотрим на уравнение, которое использует этот калькулятор уравнения Аррениуса, мы можем попытаться понять, как оно работает:
k = A * e (-Ea / (R * T))
k = константа скорости, с единицами, которые зависят от порядка реакции, n, в общем виде M1-n * s-1;
A = предэкспоненциальный фактор, иногда называемый константой Аррениуса, в тех же единицах, что и константа скорости;
e ≈ 2,72 = число Эйлера (показатель степени);
Ea = энергия активации реакции, Дж * моль-1;
R = универсальная газовая постоянная, равная 8,314 Дж * К-1 * моль-1; а также
T = температура, в К.
Указанный выше n — это порядок рассматриваемой реакции.
Что означает энергия активации Eₐ?
Теперь, как уравнение Аррениуса работает для определения константы скорости? Что ж, мы начнем с R * T. Умножая эти два значения вместе, мы получаем энергию молекул в системе в Дж * моль-1 при температуре T.
Затем мы можем разделить Ea на это число, что дает нам безразмерное число, представляющее количество столкновений, которые происходят с достаточной энергией, чтобы преодолеть требования к энергии активации (если мы не принимаем во внимание ориентацию). Это число обратно пропорционально количеству успешных столкновений. Таким образом, чем он ниже, тем больше удачных столкновений. Например, для заданного времени t значение Ea / (R * T) = 0,5 означает, что происходит вдвое больше успешных столкновений, чем если бы Ea / (R * T) = 1, что, в свою очередь, имеет вдвое больше количество успешных коллизий, чем Ea / (R * T) = 2.
Как вы, возможно, знаете, два простых способа увеличения константы скорости реакции — это либо увеличить энергию в системе и, следовательно, увеличить количество успешных столкновений (за счет увеличения температуры T), либо предоставить молекулам катализатор, который обеспечивает альтернативный путь реакции, который имеет более низкую энергию активации (более низкий Ea). Чтобы сделать это справедливым для Ea / (R * T) и, следовательно, удалить его обратно пропорциональный характер, мы умножаем его на -1, получая -Ea / (R * T).
Что такое уравнение Аррениуса — e, A и k?
По мере увеличения температуры реакции количество успешных столкновений также увеличивается экспоненциально, поэтому мы увеличиваем экспоненциальную функцию e на -Ea / RT, получая e (-Ea / RT). Это представляет собой вероятность того, что любое данное столкновение приведет к успешной реакции.
Теперь, как мы упоминали выше, даже если две молекулы сталкиваются с достаточной энергией, они все равно могут не реагировать; они могут не иметь правильной ориентации относительно друг друга, так что конструктивного орбитального перекрытия не происходит. Следовательно, часть всех столкновений является безуспешной, что представлено как A. Мы умножаем это число на e (-Ea / RT), получая A * e (-Ea / RT), частоту, с которой столкновение приведет к успешной реакции. , или константа скорости, k.
Уравнение Аррениуса kB
Возможно, вы заметили, что приведенное выше объяснение уравнения Аррениуса касается вещества на основе на моль, но что, если вы хотите найти одну из переменных на основе расчета на молекулу? Что ж, в этом случае изменение довольно простое; вы замените универсальную газовую постоянную R на постоянную Больцмана kB и сделайте единицы энергии активации J * молекула-1:
k = A * e (-Ea / (кБ * T))
k = константа скорости, с единицами, которые зависят от порядка реакции, n, в общем виде M1-n * s-1;
A = предэкспоненциальный фактор, иногда называемый константой Аррениуса, в тех же единицах, что и константа скорости;
e ≈ 2,72 = число Эйлера (показатель степени);
Ea = энергия активации реакции, Дж * молекула-1;
kB = постоянная Больцмана, равная 1,380649 × 10−23 Дж * K-1; а также
T = температура, в К.
Калькулятор уравнения Аррениуса также позволяет выполнять вычисления с использованием этой формы, выбирая параметр для каждой молекулы в самом верхнем поле.
Уравнение Аррениуса ln и график уравнения Аррениуса
Что замечательно в уравнении Аррениуса, так это то, что, решив его однажды, вы можете найти константу скорости реакции при любой температуре. Сложность в том, что экспоненциальная функция — не очень приятная графическая форма для работы. Итак, если вам нужен график уравнения Аррениуса, вы, скорее всего, будете использовать форму ln уравнения Аррениуса:
ln (k) = -Ea / R * 1 / T + ln (A)
Это имеет поразительное сходство с уравнением для прямой линии y = mx + c, где
у = ln (k);
m = -Ea / R;
х = 1 / Т; а также
с = ln (A).
Этот калькулятор уравнения Аррениуса также позволяет вам создать свой собственный график уравнения Аррениуса! Все, что вам нужно сделать, это выбрать Да рядом с графиком Аррениуса? поле в нижней части инструмента после заполнения основной части калькулятора. Вы также можете изменить диапазон 1 / T и шаги между точками в расширенном режиме. Эта функция работает как в обычном экспоненциальном режиме, так и в режиме уравнения Аррениуса ln, а также для каждой молекулы.
Вот пример уравнения Аррениуса.
2NO2 (г) → 2NO (г) + O2 (г)
При 320 ° C NO2 разлагается с константой скорости 0,5 М * с-1. Экспериментально установлено, что энергия активации этой реакции составляет 115 кДж * моль-1. Что такое предэкспоненциальный множитель?
Первым делом вам нужно преобразовать единицы, чтобы вы могли использовать их в уравнении Аррениуса.
преобразование температуры: 320 ° C + 273,15 = 593,15 K; а также
преобразование энергии: 115 кДж * моль-1 * 1000 = 115000 Дж * моль-1.
Теперь, когда вы это сделали, вам нужно изменить уравнение Аррениуса, чтобы найти A.
Источник
