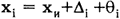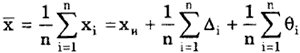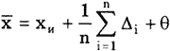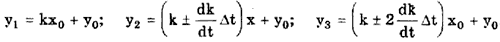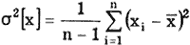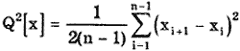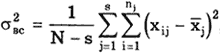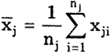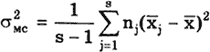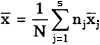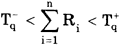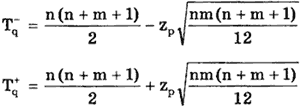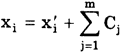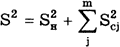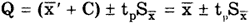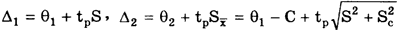Способы устранения погрешностей метрология

Методы повышения точности измерений

Анализ причин появления погрешностей измерений, выбор способов их обнаружения и уменьшения являются основными этапами процесса измерений. Погрешности измерений, принято делить на систематические и случайные. В процессе измерений систематические и случайные погрешности проявляются совместно и образуют нестационарный случайный процесс. Деление погрешностей на систематические и случайные является удобным приемом для их анализа и разработки методов уменьшения их влияния на результат измерения.

Рассмотрим способы обнаружения и исключения систематических погрешностей, поскольку они зависят от выбора метода измерений и его осуществелния.

По характеру изменения систематические погрешности делятся:

• постоянные – погрешности, связанные с неточной градуировкой шкалы прибора, отклонением размера меры от номинального значения, неточным выбором моделей объектов.
• переменные
  – периодические – погрешность изменяющаяся по периодическому закону, например погрешность отсчета при определении времени по башенным часам, если смотреть на стрелку снизу, температурная погрешность от изменения температуры в течение суток и т.п.
  – прогрессирующие – погрешности монотонно изменяющиеся (увеличивающиеся или уменьшающиеся) в общем случае по сложному, обычно неизвестному закону. Прогрессирующие погрешности во многих случаях обусловлены старением элементов средств измерений и могут быть скорректированы при его периодической поверке.

По причине возникновения погрешности измерений разделяются на три основные группы:

• методические – погрешности обусловленные неадекватностью принимаемых моделей реальным объектам, несовершенством методов измерений, упрощением зависимостей, положенных в основу измерений, неопределенностью объекта измерения;
• инструментальные – погрешности обусловленные прежде всего особенностями используемых в средствах измерений принципов и методов измерений, а также схемным, конструктивным и технологическим несовершенством средств измерений.
• взаимодейтствия – обусловлены взаимным влиянием средства измерений, объекта исследования и экспериментатора. Погрешности из-за взаимного влияния средства и объекта измерений обычно принято относить к методическим погрешностям, а погрешности, связанные с действиями экспериментатора, называются личными погрешностями. Однако такая классификация недостаточно полно отражает суть рассматриваемых погрешностей.

Выявление и устранение причин возникновения погрешностей – наиболее распространенный способ уменьшения всех видов систематических погрешностей. Примерами такого способа являются: термостатирование отдельных узлов или прибора в целом, а также проведение измерений в термостатированных помещениях для исключения температурной погрешности, применение экранов, фильтров и специальных цепей (например, эквипотенциальных цепей) для устранения погрешностей из-за влияния электромагнитных полей, наводок и токов утечек, применение стабилизированных источников питания.

Для уменьшения прогрессирующей погрешности из-за старения элементов средств измерений, параметры таких элементов стабилизируют путем искусственного и естественного старения. Кроме этого систематические погрешности можно уменьшить рациональным расположением средств измерений по отношению друг к другу, к источнику влияющих воздействий и к объекту исследования. Например магнитоэлектрические приборы должны быть удалены друг от друга, оси катушек индуктивности, должны быть расположены под углом 90°, выводы термопары должны располагаться по изотермическим линиям объекта.

Многие систематические погрешности, являющиеся не изменяющимися во времени функциями влияющих величин или обусловленные стабильными физическими эффектами, могут быть теоретически рассчитаны и устранены введением поправок или использованием специальных корректирующих цепей.

Другим радикальным способом устранения систематических погрешностей является поверки средств измерений в рабочих условиях с целью определения поправок к результатам измерения. Это дает возможность учесть все систематические погрешности без выяснения причин их возникновения. Степень коррекции систематических погрешностей в этом случае, естественно, зависит от метрологических характеристик используемых эталонных приборов и случайных погрешностей поверяемых приборов.

Фактически поверка средств измерений перед их использованием и введение поправок адекватна применению средств измерений более высоких классов точности при условии, что случайные погрешности средств измерений малы по сравнению с систематическими, а сами систематические погрешности медленно изменяются во времени.

Метод инвертирования широко используется для устранения ряда постоянных и медленно изменяющихся систематических погрешностей. Этот метод и ряд его разновидностей (метод исключения погрешности по знаку, коммутационного инвертирования, структурной модуляции, двукратных измерений, инвертирования функции преобразования и др.) основаны на выделении алгебраической суммы чесного числа сигналов измерительной информации, которые вследствие инвертирования отличаются направлением информативного сигнала, опорного сигнала или знаком погрешности.

Метод модуляции – метод близкий к методу инвертирования, в котором производится периодическое инвертирование входного сигнала и подавление помехи, имеющей однонаправленное действие.

Метод исключения погрешности по знаку — вариант метода инвертирования, который часто применяется для исключения известных по природе погрешностей, источники которых имеют направленное действие, например погрешностей из-за влияния постоянных магнитных полей, ТЭДС и др.

Метод замещения (метод разновременного сравнения) является наиболее универсальным методом, который дает возможность устранить большинство систематических погрешностей. Измерения осуществляются в два приема. Сначала по отсчетному устройству прибора делают отсчет измеряемой величины, затем, сохраняя все условия эксперимента неизменными, вместо измеряемой величины на вход прибора подают известную величину, значение которой с помощью регулируемой меры (калибратором) устанавливают таким образом, чтобы показание прибора было таким же, как при включении измеряемой величины.

Метод равномерного компарирования является разновидностью метода замещения, он используется при измерениях таких величин, которые нельзя с высокой точностью воспроизводить с помощью регулируемых мер или других технических средств. Обычно это величины, изменяющиеся с высокой частотой или по сложному закону. В качестве известных регулируемых величин при этом используются величины такого же рода, как измеряемые, но отличаютщиеся от них спектральным составом (обычно постоянные во времени и в пространстве) и создающие такой же, как и измеряемая величина, сигнал на выходе компарирующего преобразователя.

Метод эталонных сигналов заключается в том, что на вход средств измерений периодически вместо измеряемой величины подаются эталонные сигналы такого же рода, что и измеряемая величина. Разность между реальной градуировочной характеристикой используется для коррекции чувствительности или для автоматического введения поправки в результат измерения. При этом, как и при методе замещения, устраняются все систематические погрешности, но только в тех точках диапазона измерений, которые соответствуют эталонным сигналам. Метод широко используется в современных точных цифровых приборах и в информационно-измерительных системах. Примером использования этого метода является периодическая подстройка рабочего тока в компенсаторах и цифровых вольтметрах постоянного тока при помощи нормального элемента.

Тестовый метод – при использовании данного метода значение измеряемой величины определяется по результатам нескольких наблюдений, при которых в одном случае входным сигналом средства измерений является сама измеряемая величина Х, а в других – так называемые тесты, являющиеся функциями измеряемой величины.

Метод вспомагательных измерений используется для исключения погрешностей из-за влияющих величин и неинформативных параметров входного сигнала. Для реальзации этого метода одновременно с измеряемой величиной Х с помощью вспомогательных измерительных устройств производится измерение каждой из влияющих величин и вычисление с помощью вычислительного устройства, а также формул и алгоритмов поправок к результатам измерения.

Метод симметричных наблюдений заключается в проведении многократных наблюдений через равные промежутки времени и усреднении результатов наблюдений, симметрично расположенных относительно среднего наблюдения. Обычно этот метод применяется для исключения прогрессирующих погрешностей, изменяющихся по линейному закону. Так, при измерении сопротивления резистора путем сравнения напряжения на измеряемом и эталонном резисторах, включенных последовательно и питаемых от общего аккумулятора, может возникнуть погрешность вследствие разряда источника питания.
Для исключения этой погрешности проводят три измерения падения напряжения:

• на эталонном резисторе U01 = I·R0;
• через равные промежутки времени на измеряемом резисторе UX = (I — ΔI1)·RX;
• снова на эталонном резисторе U02 = (I — ΔI2)·R0.
• Если ток изменяется во времени по линейному закону, то ΔI2 = 2ΔI1; I — ΔI1 = (U01 + U02) / (2R0) и RX = R0·2·UX / (U01 + U02).

Метод симметричных наблюдений можно также использовать для устранения других видов погрешностей, например систематических погрешностей из-за влияющих величин, изменяющихся по периодическому закону. В этом случае симметричные наблюдения проводят через половину периода, когда погрешность имеет разные знаки, но одинаковые значения. Таким образом, например, можно исключить погрешность из-за наличия четных гармоник при измерении амплитудного значения напряжения при искаженной форме кривой.

Источник

Погрешности измерений и способы их устранения

Погрешность измерений или погрешность результата измерения Δ — это отклонение результата измерения X_i от истинного значения величины X_ист:

За истинное значение, которое точно неизвестно, принимается номинальный размер, среднее арифметическое ряда многократных измерений или величина, полученная более точными СИ.

Точность измерений характеризуется погрешностью измерений, которая должна стремиться к нулю.

По форме представления (нормирования) погрешности разделяются на абсолютные, относительные и приведенные.

По характеру изменения результата при повторных измерениях погрешности разделяются на систематические, случайные и промахи (грубые).

По причине возникновения погрешности разделяются на объективные и субъективные. Используя комплект измерительный К540 удается избежать больших погрешностей при измерении тока.

Основные составляющие суммарной систематической погрешности измерений:
— погрешности средств измерения (инструментальные);
— методические погрешности, обусловленные несовершенством метода измерения и построения математических зависимостей;
— погрешности установочных мер;
— погрешности, зависящие от измерительного усилия;
— температурные погрешности;
— субъективные погрешности;
— погрешность базирования.

Применяются четыре способа исключения систематических погрешностей:
1. Ликвидация источников погрешностей до начала измерения (профилактика измерений).
2. В процессе измерений (экспериментальное исключение).
3. По окончанию измерений путем добавления поправок (вычислением).
4. Перевод не исключенных систематических погрешностей в разряд случайных и выполнение многократных измерений.

После выполнения измерений в результат может быть введена поправка, равная известной систематической погрешности по величине, но обратная ей по знаку:

где X_д — действительное значение измеряемой величины, X_i — результат измерения, q — поправка.

Источник

Способы обнаружения и устранения систематических погрешностей

Результаты наблюдений, полученные при наличии систематической погрешности, называются неисправленными. При проведении измерений стараются в максимальной степени исключить или учесть влияние систематических погрешностей.

Это может быть достигнуто следующими путями:

— устранением источников погрешностей до начала измерений. В большинстве областей измерений известны главные источники систематических погрешностей и разработаны методы, исключающие их возникновение или устраняющие их влияние на результат измерения. В связи с этим в практике измерений стараются устранить систематические погрешности не путем обработки экспериментальных данных, а применением СИ, реализующих соответствующие методы измерений;

— определением поправок и внесением их в результат измерения;

— оценкой границ неисключенных систематических погрешностей.

Постоянная систематическая погрешность не может быть найдена методами совместной обработки результатов измерений. Однако она не искажает ни показатели точности измерений, характеризующие случайную погрешность, ни результат нахождения переменной составляющей систематической погрешности. Действительно, результат одного измерения

где x_и — истинное значение измеряемой величины; _i — i-я случайная погрешность; _i — i-я систематическая погрешность. После устранения результатов многократных измерении получаем среднее арифметическое значение измеряемой величины

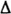
Если систематическая погрешность постоянна во всех измерениях, т.е. _i= ,то

Таким образом, постоянная систематическая погрешность не устраняется при многократных измерениях.

Постоянные систематические погрешности могут быть обнаружены лишь путем сравнения результатов измерений с другими, полученными с помощью более высокоточных методов и средств. Иногда эти погрешности могут быть устранены специальными приемами проведения процесса измерений. Эти методы рассмотрены ниже.

Наличие существенной переменной систематической погрешности искажает оценки характеристик случайной погрешности и аппроксимацию ее распределения. Поэтому она должна обязательно выявляться и исключаться из результатов измерений.

Для устранения постоянных систематических погрешностей применяют следующие методы:

— Метод замещения, представляющий собой разновидность метода сравнения, когда сравнение осуществляется заменой измеряемой величины известной величиной, причем так, что при этом в состоянии и действии всех используемых средств измерений не происходит никаких изменений. Этот метод дает наиболее полное решение задачи. Для его реализации необходимо иметь регулируемую меру, величина которой однородна измеряемой. Например, взвешивание по методу Борда, измерение сопротивления посредством моста постоянного тока и мер сопротивления.

— Метод противопоставления, являющийся разновидностью метода сравнения, при котором измерение выполняется дважды и проводится так, чтобы в обоих случаях причина постоянной погрешности оказывала разные, но известные по закономерности воздействия на результаты наблюдений. Например, способ взвешивания Гаусса.

— Метод компенсации погрешности по знаку (метод изменения знака систематической погрешности), предусматривающий измерение с двумя наблюдениями, выполняемыми так, чтобы постоянная систематическая погрешность входила в результат каждого из них с разными знаками.

— Метод рандомизации — наиболее универсальный способ исключения неизвестных постоянных систематических погрешностей. Суть его состоит в том, что одна и та же величина измеряется различными методами (приборами). Систематические погрешности каждого из них для всей совокупности являются разными случайными величинами. -Вследствие этого при увеличении числа используемых методов (приборов) систематические погрешности взаимно компенсируются.

Для устранения переменных и монотонно изменяющихся систематических погрешностей применяют следующие приемы и методы.

— Анализ знаков неисправленных случайных погрешностей.

Если знаки неисправленных случайных погрешностей чередуются с какой-либо закономерностью, то наблюдается переменная систематическая погрешность. Если последовательность знаков «+» у случайных погрешностей сменяется последовательностью знаков «-» или наоборот, то присутствует монотонно изменяющаяся систематическая погрешность. Если группы знаков «+» и «-» у случайных погрешностей чередуются, то присутствует периодическая систематическая погрешность.

— Графический метод.

Он является одним из наиболее простых способов обнаружения переменной систематической погрешности в ряду результатов наблюдений и заключается в построении графика последовательности неисправленных значений результатов наблюдений. На графике через построенные точки проводят плавную кривую, которая выражает тенденцию результата измерения, если она существует. Если тенденция не прослеживается, то переменную систематическую погрешность считают практически отсутствующей.

— Метод симметричных наблюдений.

Рассмотрим сущность этого метода на примере измерительного преобразователя, передаточная функция которого имеет вид y = kx + y₀ , где х, у — входная и выходная величины преобразователя; k — коэффициент, погрешность которого изменяется во времени по линейному закону; у₀ — постоянная.
Для устранения систематической погрешности трижды измеряется выходная величина у через равные промежутки времени At. При первом и третьем измерениях на вход преобразователя подается сигнал х0 от образцовой меры. В результате измерений получается система уравнений:

Ее решение позволяет получить значение х, свободное от переменной систематической погрешности, обусловленной изменением коэффициента k:

Специальные статистические методы. К ним относятся способ последовательных разностей, дисперсионный анализ, и др. Рассмотрим подробнее некоторые из них.

Способ последовательных разностей (критерий Аббе).

Применяется для обнаружения изменяющейся во времени систематической погрешности и состоит в следующем. Дисперсию результатов наблюдений можно оценить двумя способами: обычным

и вычислением суммы квадратов последовательных (в порядке проведения измерений) разностей ( x_i+1 — x_i) 2

Если в процессе измерений происходило смещение центра группирования результатов наблюдений, т.е. имела место переменная систематическая погрешность, то 2 [x] дает преувеличенную оценку дисперсии результатов наблюдений. Это объясняется тем, что на 2 [x] влияют вариации . В то же время изменения центра группирования весьма мало сказываются на значениях последовательных разностей d _i = x _i+1-x _i, поэтому смещения почти не отразятся на значении Q 2 [x].

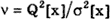
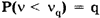
Отношение является критерием для обнаружения систематических смещений центра группирования результатов наблюдений. Критическая область для этого критерия (критерия Аббе) определяется как , где q = 1-Р — уровень значимости, Р — доверительная вероятность. Значения v_q для различных уровней значимости q и числа наблюдений n приведены в таблице. Если полученное значение критерия Аббе меньше при заданных q и n, то гипотеза о постоянстве центра группирования результатов наблюдений отвергается, т.е. обнаруживается переменная систематическая погрешность результатов измерений.

n	vq при q, равном	n	vq при q, равном
0.001	0.01	0.05	0.001	0.01	0.05
0.295	0.313	0.390	0.295	0.431	0.578
0.208	0.269	0.410	0.311	0.447	0.591
0.182	0.281	0.445	0.327	0.461	0.603
0.185	0.307	0.468	0.341	0.474	0.614
0.202	0.331	0.491	0.355	0.487	0.624
0.221	0.354	0.512	0.368	0.499	0.633
0.241	0.376	0.531	0.381	0.510	0.642
0.260	0.396	0.548	0.393	0.520	0.650
0.278	0.414	0.564

Дисперсионный анализ (критерий Фишера).

В практике измерений часто бывает необходимо выяснить наличие систематической погрешности результатов наблюдений, обусловленной влиянием какого-либо постоянно действующего фактора, или определить, вызывают ли изменения этого фактора систематическое смещение результатов измерений. В данном случае проводят многократные измерения, состоящие из достаточного числа серий, каждая из которых соответствует определенным (пусть неизвестным, но различным) значениям влияющего фактора. Влияющими факторами, по которым производится объединение результатов наблюдений по сериям, могут быть внешние условия (температура, давление и т.д.), временная последовательность проведения измерений и т.п.

После проведения N измерений их разбивают на s серий (s > 3) по n_j результатов наблюдений ( sn_j = N ) в каждой серии и затем устанавливают, имеется или отсутствует систематическое расхождение между результатами наблюдений в различных сериях. При этом должно быть установлено, что результаты в сериях распределены нормально. Рассеяние результатов наблюдений в пределах каждой серии отражает только случайные влияния, характеризует лишь случайные погрешности измерений в пределах этой серии. Характеристикой совокупности случайных внутрисерийных погрешностей будет средняя сумма дисперсий результатов наблюдений, вычисленных раздельно для каждой серии, т.е.

где x_ji — результат i-го измерения в j-й серии.
Внутрисерийная дисперсия 2 _BC характеризует случайные погрешности измерений, так как только случайные влияния обусловливают те различия (отклонения результатов наблюдений), на которых она основана. В то же время рассеяние _j различных серий обусловливается не только случайными погрешностями измерений, но и систематическими различиями (если они существуют) между результатами наблюдений, сгруппированными по сериям. Следовательно, усредненная межсерийная дисперсия

где , выражает силу действия фактора, вызывающего систематические различия между сериями.

Таким образом, 2 _BC /( 2 _BC + 2 _MC) характеризует долю дисперсии всех результатов наблюдений, обусловленную наличием случайных погрешностей измерений, а 2 _MC /( 2 _BC + 2 _MC) — долю дисперсии, обусловленную межсерийными различиями результатов наблюдений. Первую из них называют коэффициентом ошибки, вторую — показателем дифференциации. Чем больше отношение показателя дифференциации к коэффициенту ошибки, тем сильнее действие фактора, по которому группировались серии, и тем больше систематическое различие между ними.

Критерием оценки наличия систематических погрешностей в данном случае является дисперсионный критерий Фишера F = 2 _MC 2 _BC. Критическая область для критерия Фишера соответствует P (F>F_q) = q.

Значения F_q для различных уровней значимости q, числа измерений N и числа серий s приведены в приложении 1, где k₂ = N-s , k₁ = s-1. Если полученное значение критерия Фишера больше F_q (при заданных q, N и s), то гипотеза об отсутствии систематических смещений результатов наблюдений по сериям отвергается, т.е. обнаруживается систематическая погрешность, вызываемая тем фактором, по которому группировались результаты наблюдений.

Из всех рассмотренных способов обнаружения систематических погрешностей дисперсионный анализ является наиболее эффективным и достоверным, так как позволяет не только установить факт наличия погрешности, но и дает возможность проанализировать источники ее возникновения.

Если закон распределения результатов измерений неизвестен, то для обнаружения систематической погрешности применяют статистический критерий Вилкоксона.

Из двух групп результатов измерений x₁, x₂. x_n и y₁, y₂. y_m , n> = m> = 5 , составляется вариационный ряд, в котором все n + m значений x₁, x₂. x_n и y₁, y₂. y_m располагают в порядке их возрастания и приписывают им ранги — порядковые номера членов вариационного ряда. Различие средних значений каждого из рядов можно считать допустимым, если выполняется неравенство

где R_i — ранг (номер) члена x_i, равный его номеру в вариационном ряду T — _q и T + _q — нижнее и верхнее критические значения для выбранного уровня значимости q.

При mm>15 они рассчитываются по формулам:

где z_p — квантиль нормированной функции Лапласа.

Таблица. Критические значения T_q — и T_q + при q=0.05 и 0,01

n	m	q=0.05	q=0.01
Tq —	Tq +	Tq —	Tq +

Исключение систематических погрешностей путем введения поправок.

В ряде случаев систематические погрешности могут быть вычислены и исключены из результата измерения. Для этого используются поправки. Поправка C_j — величина, одноименная измеряемой, которая вводится в результат измерения x_i = x_i ‘ + _j + C_j с целью исключения составляющих систематической погрешности _j. При C_j = —_j j-я составляющая систематической погрешности полностью устраняется из результата измерения. Поправки определяются экспериментально или в результате специальных теоретических исследований. Они задаются в виде таблиц, графиков или формул.

Введением одной поправки устраняется влияние только одной составляющей систематической погрешности. Для устранения всех составляющих в результат измерения приходится вводить множество поправок. При этом вследствие ограниченной точности определения поправок случайные погрешности результата измерения накапливаются и его дисперсия увеличивается. Так как поправка известна с определенной точностью, то она характеризуется статистически — средним значением поправки С и СКО S_c. При исправлении результата x_i ‘ путем введения поправок C_j , где j = l, 2. m, по формуле

дисперсия исправленного результата

где S_н 2 — оценка дисперсии неисправленного результата; S_cj 2 — оценка дисперсии j-й поправки. Как видно, с одной стороны, уточняется результат измерения, а с другой — увеличивается разброс за счет роста дисперсии. Следовательно, необходимо найти оптимум.
Пусть при измерении постоянной величины Q получено значение Q = ‘ t _pS ,где — оценка среднего арифметического неисправленного результата измерений; t_p — коэффициент Стьюдента.

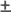
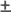
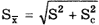
После введения поправки C t_pS_c результат измерения

где .
Максимальные доверительные значения погрешности результата измерения до и после введения поправки равны соответственно

Поправку имеет смысл вводить до тех пор, пока 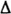₁ 0.5S_c 2 /S 2 . Из этого неравенства видно, что если оценка среднего квадратического отклонения поправки S_c стремится к нулю, то поправку имеет смысл вводить всегда. В практических расчетах погрешность результата обычно выражается не более чем двумя значащими цифрами, поэтому поправка, если она меньше пяти единиц младшего разряда, следующего за последним десятичным разрядом погрешности результата, все равно будет потеряна при округлении и вводить ее не имеет смысла.

Источник