Способы устранения автокорреляции случайных возмущений авторегрессионное преобразование
4.4. Автокорреляция возмущений: определение, диагностика и процедуры устранения
Рассмотрим линейную регрессию
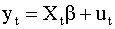 |
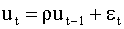 |
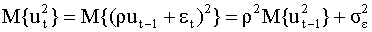 |
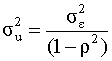 |
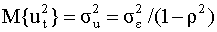 |
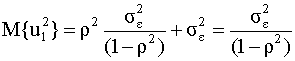 |
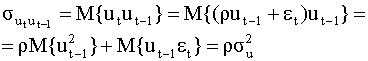 |
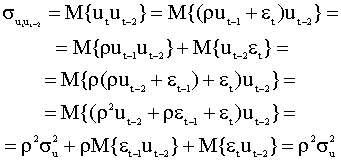 |
В общем случае точно также можно показать, что
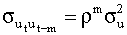 |
Таким образом, ковариационная матрица 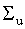
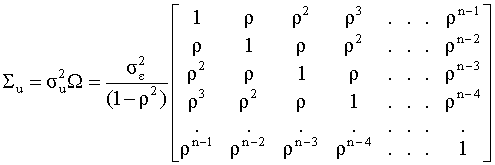 |
Эта матрица отличается от диагональной, поэтому для оценивания модели с автокорреляцией возмущений необходимо использовать обобщенный метод наименьших квадратов. Очевидно, что элементы матрицы 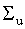
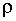
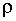
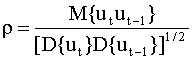 |
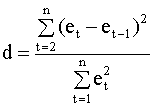 |
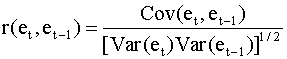 |
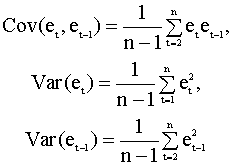 |
Для выборки достаточно большого размера можно записать приближенное соотношение
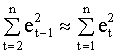 |
учитывая которое, выборочный коэффициент корреляции ( 4.38 ) можно представить так
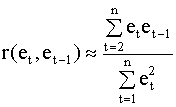 |
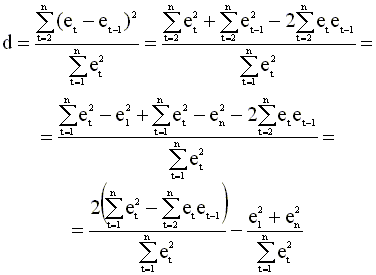 |
Последнее слагаемое в полученном выражении близко к нулю и им можно пренебречь (при достаточно большом n). Тогда окончательно (учитывая ( 4.39 )) получаем
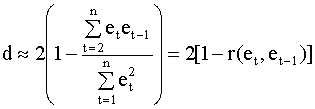 |
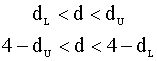 |
4) . Интерпретируем результаты тестирования.
Следует помнить, что корректное применение d — теста требует выполнения предпосылки о некоррелированности регрессоров и возмущений модели. Поэтому его нельзя применять, если, например, в модели присутствуют лаговые (запаздывающие) значения регрессанда в качестве регрессоров (подобные модели часто используются для описания авторегрессионных временных рядов, см. гл. 5 ).
Наличие зон неопределенности существенно снижает эффективность практического использования d — теста. Ошибочное принятие гипотезы H0 приводит к существенному искажению результатов и потере свойств оценок. В тоже время, отклонение нулевой гипотезы, хотя она и верна, приведет лишь к необходимости проведения незначительных дополнительных вычислений, связанных с оценкой параметра авторегрессии 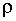
В таблице 4.2 приведены данные о годовых доходностях акций компаний A и B (источник: Л.О. Бабешко, 2001, с. 63, [ 4 ]).
Таблица 4.2 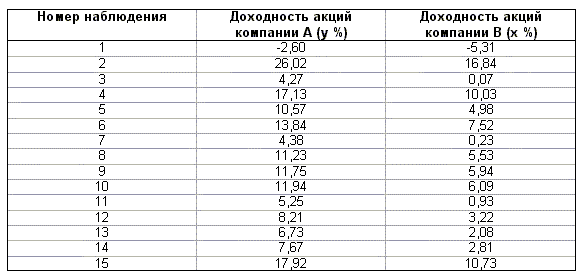
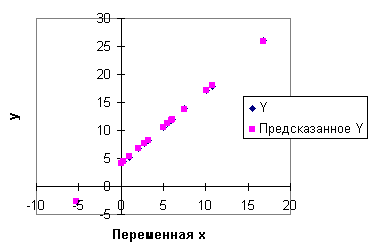
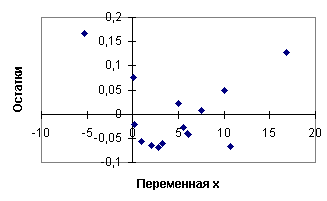
Используя данные таблицы 4.2 построим линейную регрессионную модель для изучения влияния изменения доходности акций компании — лидера B на доходность акций компании A и исследуем остатки полученной модели на автокорреляцию, применяя процедуру Дарбина — Уотсона. Спецификация модели имеет вид
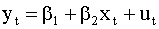 |
где yt — доходность акций компании A, xt — доходность акций компании B. Применение метода наименьших квадратов для оценки коэффициентов модели позволяет получить следующую эмпирическую функцию регрессии:
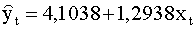 |
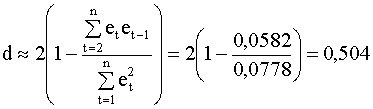 |
Для количества наблюдений n = 15, количества регрессоров k = 2 и уровня значимости 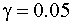
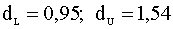
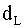
Определите для данной модели коэффициент детерминации, стандартные отклонения и доверительные интервалы для коэффициентов.
Оценка авторегрессионного параметра и процедуры устранения автокорреляции
Предположим сначала, что значение параметра авторегрессии 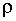
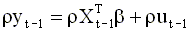 |
Учитывая уравнение авторегрессии ( 4.30 ), получим
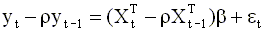 |
При t = 1 обе части уравнения ( 4.29 ) умножим на множитель 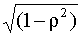
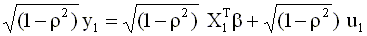 |
Введем новые переменные:
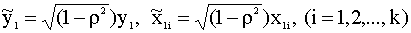 |
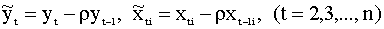 |
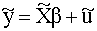 |
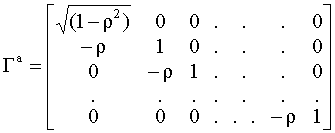 |
В преобразованной модели ( 4.44 ) возмущения удовлетворяют свойству гомоскедастичности. Действительно, компоненты вектора возмущений 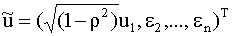
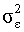
При практической реализации описанного метода, для простоты часто ограничиваются только преобразованием вида ( 4.43 ), опуская первое наблюдение ( 4.42 ).
К сожалению, при построении эконометрических моделей реальных социально-экономических процессов параметр авторегрессии, как правило, неизвестен и подлежит оцениванию. Существует множество различных процедур оценивания регрессионных моделей с одновременным оцениванием параметра авторегрессии возмущений. Рассмотрим некоторые из них.
Итерационная процедура Кохрейна-Оркатта
При подтверждении гипотезы о существовании автокорреляции первого порядка, процедура оценивания параметров регрессии с использованием преобразованной модели может быть проведена по следующей итерационной схеме.
1) Оцениваем обычным методом наименьших квадратов вектор коэффициентов исходной (не преобразованной) модели по формуле ( 3.15 ). Вычисляем вектор остатков e.
2) Оцениваем авторегрессионный параметр 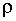
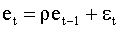
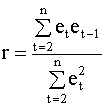 |
Заметим, что данная оценка совпадает с выборочным коэффициентом корреляции ( 4.39 ).
3) Строим преобразованную модель, используя вместо параметра 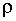
4) Вычисляем новый вектор остатков e = y — Xb. Повторяем процедуру, начиная с пункта 2). Итерационный процесс заканчивается, когда два последовательных значения оценок r параметра 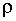
Для вычисления оценки r можно использовать соотношение ( 4.40 ), из которого получаем: 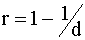
Итерационная процедура Хилдрета-Лу
1) Выбираем последовательно значения коэффициента 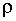
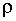
2) Для каждого значения 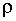
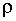
Данную процедуру можно проводить в несколько этапов — сначала определить «грубое» значение 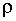
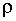
Преобразованную модель ( 4.44 ) можно записать в виде
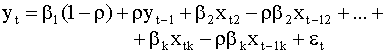 |

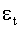 — последовательность некоррелированных случайных величин с характеристиками: математическим ожиданием
— последовательность некоррелированных случайных величин с характеристиками: математическим ожиданием 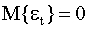 , и постоянной дисперсией
, и постоянной дисперсией 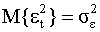 . Начальное значение u0 имеет нулевое математическое ожидание и не зависит от
. Начальное значение u0 имеет нулевое математическое ожидание и не зависит от 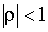 , которое является необходимым условием стационарности процесса.
, которое является необходимым условием стационарности процесса.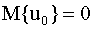 , получим
, получим 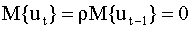 для любого t=1,2,…,n. Далее, поскольку
для любого t=1,2,…,n. Далее, поскольку 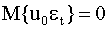 , а случайные величины
, а случайные величины 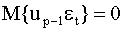 для всех p=1,2,…,t-1, в силу рекуррентной зависимости ( 4.30 ) ( задание : покажите, что это действительно так). Учитывая это, получим выражение для дисперсии
для всех p=1,2,…,t-1, в силу рекуррентной зависимости ( 4.30 ) ( задание : покажите, что это действительно так). Учитывая это, получим выражение для дисперсии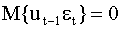 . Аналогично получим
. Аналогично получим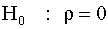 — автокорреляция отсутствует, против альтернативы
— автокорреляция отсутствует, против альтернативы 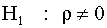 — возмущения автокоррелированы (или в двух других версиях:
— возмущения автокоррелированы (или в двух других версиях: 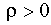 — существует положительная корреляция,
— существует положительная корреляция, 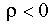 — существует отрицательная корреляция).
— существует отрицательная корреляция).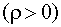 , то величина
, то величина 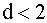 . При высокой положительной корреляции коэффициент корреляции r будет близок к единице, а d — статистика — к нулю. При отрицательной корреляции
. При высокой положительной корреляции коэффициент корреляции r будет близок к единице, а d — статистика — к нулю. При отрицательной корреляции 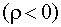 значение
значение 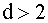 , а поскольку
, а поскольку 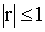 , то для d — статистики выполняются неравенства
, то для d — статистики выполняются неравенства 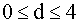 .
.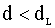 , то существует положительная корреляция, гипотеза H0 отвергается;
, то существует положительная корреляция, гипотеза H0 отвергается;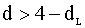 , то существует отрицательная корреляция, гипотеза H0 отвергается;
, то существует отрицательная корреляция, гипотеза H0 отвергается;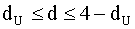 , то корреляция отсутствует, гипотеза H0 не отвергается;
, то корреляция отсутствует, гипотеза H0 не отвергается;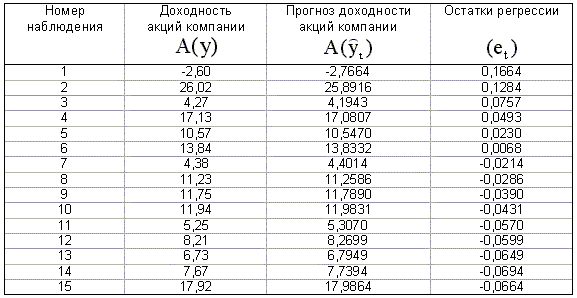
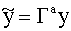 , матрица
, матрица 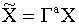 , вектор возмущений
, вектор возмущений 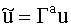 , матрица преобразования
, матрица преобразования 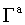 имеет следующую структуру
имеет следующую структуру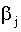 , j=2,3,…,k, исходной модели, k-1 параметр вида
, j=2,3,…,k, исходной модели, k-1 параметр вида 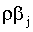 , параметр вида
, параметр вида 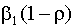 и параметр
и параметр 


