Способы устного счета деление

Эффективные способы быстрого счета в уме

Многие спрашивают, как научиться быстро считать в уме, чтобы это выглядело незаметно и неглупо. Ведь современные технологии позволяют меньше пользоваться своей памятью и умственными способностями. Но иногда нет под рукой данных технологий и порой легче и быстрее посчитать что-то в уме. Многие люди начали считать на калькуляторе или телефоне даже элементарные вещи, что также не очень хорошо. Умение считать в уме остается полезным навыком и для современного человека, несмотря на то, что он владеет всевозможными устройствами, способными считать за него. Возможность обходиться без специальных девайсов и в нужный момент оперативно решить поставленную арифметическую задачу – это не единственное применение данного навыка. Помимо утилитарного назначения, приемы устного счета позволят научиться организовывать себя в различных жизненных ситуациях. Кроме того, умение считать в уме, несомненно, положительно скажется на имидже ваших интеллектуальных способностей и выделит вас среди окружающих «гуманитариев».

Способы быстрого счета

Существует определенный набор простейших арифметических правил и закономерностей, которые не только нужно знать для устного счета, но и постоянно держать в голове, чтобы в нужный момент оперативно применить самый эффективный алгоритм. Для этого необходимо довести их использование до автоматизма, закрепить в машинальной памяти, чтобы от решения самых простых примеров успешно перейти к более сложным арифметическим действиям. Вот основные алгоритмы, которые нужно знать, помнить и применять мгновенно, автоматически:

Вычитание 7, 8, 9

Чтобы вычесть 9 из любого числа, нужно вычесть из него 10 и прибавить 1. Чтобы вычесть 8 из любого числа, нужно вычесть из него 10 и прибавить 2. Чтобы вычесть 7 из любого числа, нужно вычесть из него 10 и прибавить 3. Если обычно вы считаете по-другому, то для лучшего результата вам нужно привыкнуть к этому новому способу.

Умножение на 9

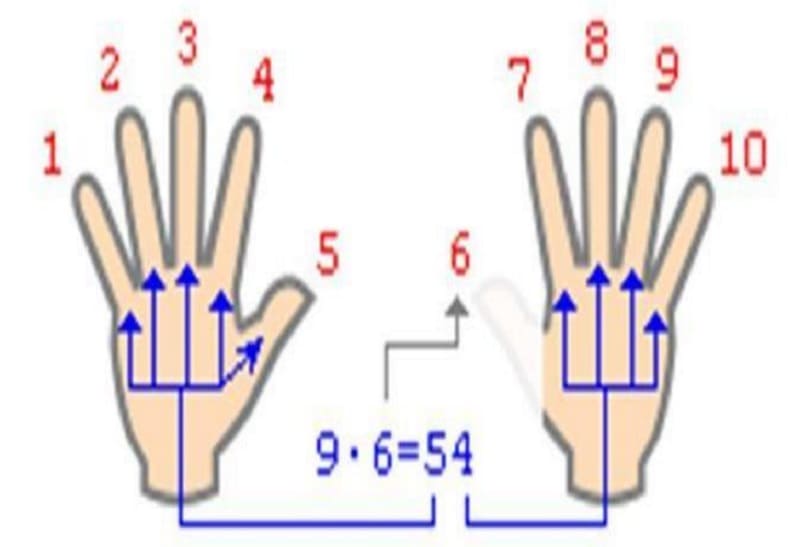
Быстро умножить любое число на 9 можно при помощи пальцев рук.

Деление и умножение на 4 и 8

Деление (или умножение) на 4 и на 8 являются двукратным или трехкратным делением (или умножением) на 2. Производить эти операции удобно последовательно.

Например, 46*4=46*2*2 =92*2= 184.

Умножение на 5

Умножать на 5 очень просто. Умножение на 5, и деление на 2 – это практически одно и то же. Так 88*5=440, а 88/2=44, поэтому всегда умножайте на 5, поделив число на 2 и умножив его на 10.

Умножение на 25

Умножение на 25 соответствует делению на 4 (с последующим умножением на 100). Так 120*25 = 120/4*100=30*100=3000.

Умножение на однозначные числа

Чтобы быстро считать в уме, полезно уметь умножать двузначные и трехзначные числа на однозначные. Для этого нужно умножать двух- или трехзначное число поразрядно.

Например, умножим 83*7.

Для этого сначала умножим 8 на 7 (и допишем ноль, так как 8 — разряд десятков), и прибавим к этому числу произведение 3 и 7. Таким образом, 83*7=80*7 +3*7= 560+21=581.

Возьмем более сложный пример: 236*3.

Итак, умножаем сложное число на 3 по разрядно: 200*3+30*3+6*3=600+90+18=708.

Определение диапазонов

Чтобы не запутаться в алгоритмах и по ошибке не выдать совсем неверный ответ, важно уметь строить примерный диапазон ответов. Так умножение однозначных чисел друг на друга может дать результат не более 90 (9*9=81), двузначных — не более 10 000 (99*99=9801), трехзначных не более — 1 000 000 (999*999=998001).

Раскладка на десятки и единицы

Способ заключается в разбиении обоих множителей на десятки и единицы с последующим перемножением получившихся четырех чисел. Этот метод достаточно прост, но требует умения удерживать в памяти одновременно до трех чисел и при этом параллельно производить арифметические действия.

63*85 = (60+3)*(80+5) = 60*80 + 60*5 +3*80 +3*5=4800+300+240+15=5355

Проще такие примеры решаются в 3 действия:

1. Сначала умножаются десятки друг на друга.
2. Потом складываются 2 произведения единиц на десятки.
3. Затем прибавляется произведение единиц.

Схематично это можно описать так:

— Первое действие: 60*80 = 4800 — запоминаем
— Второе действие: 60*5+3*80 = 540 – запоминаем
— Третье действие: (4800+540)+3*5= 5355 – ответ

Для максимально быстрого эффекта потребуется хорошее знание таблицы умножения чисел до 10, умение складывать числа (до трехзначных), а также способность быстро переключать внимание с одного действия на другое, держа предыдущий результат в уме. Последний навык удобно тренировать путем визуализации совершаемых арифметических операций, когда вы должны представлять себе картинку вашего решения, а также промежуточные результаты.

Мысленная визуализация умножения в столбик

56*67 – посчитаем в столбик. Наверное, счет столбиком содержит максимальное количество действий и требует постоянно держать в уме вспомогательные числа.

Но его можно упростить:
Первое действие: 56*7 = 350+42=392
Второе действие: 56*6=300+36=336 (ну или 392-56)
Третье действие: 336*10+392=3360+392=3 752

Частные методики умножения двузначных чисел до 30

Преимуществом трех способов умножения двузначных для устного счета состоит в том, что они универсальны для любых чисел и при хорошем навыке устного счета, они могут позволить вам достаточно быстро прийти к правильному ответу. Однако эффективность умножения некоторых двузначных чисел в уме может быть выше за счет меньшего количества действий при использовании специальных алгоритмов.

Умножение на 11

Чтобы умножить любое двузначное число на 11, нужно между первой и второй цифрой умножаемого числа вписать сумму первой и второй цифры.

Например: 23*11, пишем 2 и 3, а между ними ставим сумму (2+3). Или короче, что 23*11= 2 (2+3) 3 = 253.

Если сумма чисел в центре дает результат больше 10, тогда добавляем единицу к первой цифре, а вместо второй цифры пишем сумму цифр умножаемого числа минус 10.

Например: 29*11 = 2 (2+9) 9 = 2 (11) 9 = 319.
Быстро умножать на 11 устно можно не только двузначные числа, но и любые другие числа.

Например: 324 * 11=3(3+2)(2+4)4=3564

Квадрат суммы, квадрат разности

Для того чтобы возвести в квадрат двузначное число, можно воспользоваться формулами квадрата суммы или квадрата разности. Например:

23²= (20+3)2 = 202 + 2*3*20 + 32 = 400+120+9 = 529

69² = (70-1)2 = 702 – 70*2*1 + 12 = 4 900-140+1 = 4 761

Возведение в квадрат чисел, заканчивающихся на 5.Чтобы возвести в квадрат числа, заканчивающиеся на 5. Алгоритм прост. Число до последней пятерки, умножаем на это же число плюс единица. К оставшемуся числу дописываем 25.

25² = (2*(2+1)) 25 = 625

85² = (8*(8+1)) 25 = 7 225

Это верно и для более сложных примеров:

155² = (15*(15+1)) 25 = (15*16)25 = 24 025

Методика умножения чисел до 20 очень проста:

16*18 = (16+8)*10+6*8 = 288

Доказать правильность этого метода просто: 16*18 = (10+6)*(10+8) = 10*10+10*6+10*8+6*8 = 10*(10+6+8) +6*8. Последнее выражение и является демонстрацией описанного выше метода. По сути, этот метод является частным способом использования опорных чисел . В данном случае опорным числом является 10. В последнем выражении доказательства видно, что именно на 10 мы умножаем скобку. Но в качестве опорного числа можно использовать и любые другие числа, из которых наиболее удобными являются 20, 25, 50, 100…

Опорное число

Посмотрите на суть этого метода на примере умножения 15 и 18. Здесь удобно использовать опорное число 10. 15 больше десяти на 5, а 18 больше десяти на 8.

Для того, чтобы узнать их произведение, нужно совершить следующие операции:

15*18

1. К любому из множителей прибавить число, на которое второй множитель больше опорного. То есть прибавить 8 к 15, или 5 к 18. В первом и втором случае получается одно и то же: 23.
2. Затем 23 умножаем на опорное число, то есть на 10. Ответ: 230
3. К 230 прибавляем произведение 5*8. Ответ: 270.

Опорное число при умножении чисел до 100.Наиболее популярной методикой умножения больших чисел в уме является прием использования, так называемого, опорного числа
Опорное число при умножении – это число, к которому близко находятся оба множителя и на которое удобно умножать. При умножении чисел до 100 опорными числами удобно использовать все числа кратные 10, а особенно 10, 20, 50 и 100.
Методика использования опорного числа зависит от того, являются ли множители больше или меньше опорного числа. Тут возможны три случая. Покажем, все 3 методики на примерах.
Оба числа меньше опорного (под опорным). Допустим, мы хотим умножить 48 на 47.
Эти числа находятся достаточно близко к числу 50, а следовательно удобно использовать 50 в качестве опорного числа.
Чтобы умножить 48 на 47, используя опорное число 50, нужно:

47*48

1. Из 47 вычесть столько, сколько не хватает 48 до 50, то есть 2. Получается 45 (или
из 48 вычесть 3 – это всегда одно и то же)
2. Дальше 45 умножаем на 50 = 2250
3. Затем прибавляем 2*3 к этому результату – 2 256

50 (опорное число)

Если числа меньше опорного, то из первого множителя вычитаем разность между опорным числом и вторым множителем. Если числа больше опорного, то к первому множителю прибавляем разность опорного числа и второго множителя .

Одно число под опорным, а другое над.Третий случай использования опорного числа – когда одно число больше опорного, а другое меньше. Такие примеры решаются не сложнее, чем предыдущие. Меньший множитель увеличиваем на разность между вторым множителем и опорным числом, результат умножаем на опорное число и вычитаем произведение разностей опорного числа и множителей. Или больший множитель уменьшаем на разность между вторым множителем и опорным числом, результат умножаем на опорное число и вычитаем произведение разностей опорного числа и множителей.

(52-5)*50-5*2=47*50-10=2340 или (45+2)*50-5*2=47*50-10=2340

При умножении двузначных чисел из разных десятков в качестве опорного числа удобнее
брать круглое число , которое больше большего множителя.

27*89

Таким образом, с помощью использования одного опорного числа можно умножать большую комбинацию двузначных чисел. Описанные выше методики можно разделить на универсальные (подходящие для любых чисел) и частные (удобные для конкретных случаев).

В крайнем случае, можно воспользоваться «крестьянским» счетом. Чтобы умножить одно число на другое, допустим 21*75, нам нужно записать числа в две колонки. Первое число левой колонки 21, первое число правого столбика 75. Затем числа стоящие в левой колонке делить на 2 и отбрасывать остаток, пока не получим единицу, а числа в правой колонке умножаем на 2. Все строчки, имеющие четные числа в левой колонке вычеркиваем, а оставшиеся числа в правой колонке складываем, у нас получается точный результат.

21*75

Чтобы научиться быстро считать в уме, нужна практика, нет волшебных методик, чтобы с первого раза начать быстро считать в голове, необходимо постоянно тренировать свой мозг и заставлять его быстро работать и считать.

Заключение

Как и все способы вычислений, данные методы быстрого счета имеют свои достоинства и недостатки:

ПЛЮСЫ:

1.С помощью различных методов быстрых вычислений даже самый малообразованный человек может считать.
2. Способы быстрого счета могут помочь избавиться от сложного действия, путем замены его на несколько более простых.
3.Способы быстрого счета полезны в ситуациях, когда нельзя воспользоваться умножением в столбик.
4.Способы быстрого счета позволяют сократить время вычислений.
5.Устный счет развивает умственную деятельность, что помогает быстрее ориентироваться в сложных жизненных ситуациях.
6. Техника устного счета делает процесс вычислений более увлекательным и интересным.

МИНУСЫ:

1.Зачастую, решать пример, пользуясь способами быстрого счета, оказывается дольше, чем просто перемножать в столбик, так как приходится выполнять большее количество действий, каждое из которых проще первоначального.
2.Бывают ситуации, когда человек от волнения или еще чего-то забывает способы быстрого счета или вовсе — путается в них; в таких случаях ответ получается неправильным, а способы являются фактически бесполезными.
3.Не для всех случаев разработаны способы быстрого счета .
4.Вычисляя с использованием техники быстрого счета, нужно держать множество ответов в голове, в чем можно запутаться и прийти к ошибочному результату.

Несомненно, практика играет важнейшую роль в развитии любых способностей. Но навык устного счета не опирается на один лишь опыт. Это доказывают люди, которые способны считать в уме сложные примеры. Например, такие люди могут умножать и делить трехзначные числа, совершать арифметические операции, которые не каждый человек и в столбик сможет посчитать. Что же необходимо знать и уметь обычному человеку, чтобы овладеть такой феноменальной способностью? На сегодняшний день существуют различные методики, помогающие научиться быстро считать в уме.

Изучив многие подходы к обучению навыку считать устно, можно выделить 3 основных составляющих данного навыка:

1. Способности. Способность концентрировать внимание и умение удерживать в краткосрочной памяти несколько вещей одновременно. Предрасположенность к математике и логическому мышлению.

2. Алгоритмы. Знание специальных алгоритмов и умение оперативно подобрать нужный, максимально эффективный алгоритм в каждой конкретной ситуации.

3. Тренировка и опыт, значение которых для любого навыка никто не отменял. Постоянные тренировки и постепенное усложнение решаемых задач и упражнения позволят вам улучшить скорость и качество устного счета. Нужно отметить, что третий фактор имеет ключевое значение. Не обладая необходимым опытом, вы не сможете удивить окружающих быстрым счетом, даже если вы знаете самый удобный алгоритм. Однако не стоит недооценивать важность первых двух составляющих, поскольку имея в своем арсенале способности и набор нужных алгоритмов, вы сможете удивить даже самого опытного «счетовода», при условии, что вы тренировались одинаковое время.

Источник

Способы устного счета деление

Устный счет – гимнастика для ума. Способы сложения, вычитания, умножения, деления, для производства которых, достаточно устного счета. Мотивацией для выбора темы послужило умения быстро и чётко находить результат математических действий. Говорят, если хотите уметь решать задачи, то должны начать их решать. Научиться считать быстро, считать в уме можно только при большом желании и систематической тренировке в решении задач.

Приёмы устного счёта известны давно. Великолепные способности к устному счёту таких блестящих математиков, как Гаусс, фон Нейман, Эйлер или Валлис, у многих вызывают настоящий восторг. Об этом много написано. Мы хотим рассказать и показать некоторые известные вычислительные секреты. И тогда перед вами откроется совсем другая математика. Живая, полезная и понятная.

Для того чтобы понять, какую роль в нашей жизни играют цифры, поставьте простой эксперимент. Попробуйте некоторое время обойтись без них. Без цифр, без вычислений, без измерений… Вы окажетесь в странном мире, где почувствуете себя абсолютно беспомощным, связанным по рукам и ногам. Как успеть на встречу вовремя? Отличить один автобус от другого? Позвонить по телефону? Купить хлеб, колбасу, чай? Сварить суп или картошку? Без чисел, а значит, без счета жизнь невозможна. Но как тяжело иногда дается эта наука! Попробуйте быстро перемножить 65 на 23? Не получается? Рука сама тянется за мобильником с калькулятором. А, между тем, полуграмотные русские крестьяне 200 лет назад спокойно делали это, пользуясь лишь первым столбиком таблицы умножения — умножением на два. Не верите? А зря. Это — реальность.

«Компьютер» каменного века

Даже не зная чисел, люди уже пытались считать. Если нашим предкам, обитавшим в пещерах и носившим шкуры, нужно было поменяться чем-либо с соседним племенем, они поступали просто: расчищали площадку и выкладывали, например, наконечник стрелы. Рядом ложилась рыба или горсть орехов. И так до тех пор, пока не заканчивался один из обменных товаров, или глава «торговой миссии» не решал, что уже хватит. Примитивно, но по-своему очень удобно: и не запутаешься, и не обманут.

С освоением скотоводства задачи усложнились. Большое стадо нужно было как-то считать, чтобы знать, все ли козы или коровы на месте. «Счетной машиной» неграмотных, но умных пастухов стала долбленая тыква с камешками. Как только животное покидало загон, пастух клал в тыкву камешек. Вечером стадо возвращалось, и пастух вынимал по камешку с каждым входившим в загон животным. Если тыква пустела, он знал, что со стадом все в порядке. Если оставались камешки — шел искать потерю.

Когда появились цифры, дело пошло веселее. Хотя еще долго у наших предков в ходу было лишь три числительных: «один», «пара» и «много».

Можно ли считать быстрее компьютера? Обогнать устройство, выполняющее сотни миллионов операций в секунду? Невозможно… Но тот, кто говорит так, жестоко лукавит, или просто кое-что умышленно упускает из вида. Компьютер — это лишь набор микросхем в пластике, он не считает сам по себе.

Поставим вопрос по-другому: может ли человек, считая в уме, обогнать того, кто выполняет вычисления на компьютере? И здесь ответ — да. Ведь, чтобы получить ответ от «черного чемоданчика», данные в него необходимо сначала ввести. Это будет делать человек при помощи пальцев или голосом. А все эти действия имеют ограничения по времени. Непреодолимые ограничения. Сама природа поставила их человеческому телу. Всему — кроме одного органа. Мозга!

Калькулятор умеет выполнять лишь две операции: сложение и вычитание. Умножение для него — это множественное сложение, а деление — множественное вычитание.

Наш мозг поступает по-другому. Класс, где учился будущий король математики, Карл Гаусс, как-то получил задание: сложить все числа от 1 до 100. Карл написал на своей доске абсолютно правильный ответ, как только учитель закончил объяснять задание. Он не стал прилежно складывать числа по порядку, как поступил бы любой уважающий себя компьютер. Он применил открытую им самим формулу: 101 х 50 = 5050. И это далеко не единственный прием, ускоряющий вычисления в уме.

Данная тема является одной из самых актуальных. Выработка навыков устного счёта занимает особое место в школе и является одной из главных задач обучения математике на этом этапе. Именно в первые годы обучения закладываются основные приёмы устных вычислений, которые активизируют мыслительную деятельность учеников, развивают память, речь, способность воспринимать на слух сказанное, повышают внимание и быстроту реакции.

Объект исследования: Математика.

Предмет исследования: Устный счет

Узнать о способах и приемах устного счета.

Составить историческую справку по данной теме

Рассмотреть все возможные элементы и приемы устного счета.

Доказать, что эти приемы действительно помогают.

В жизни существует много различных способов и приемов устного счета.

У́стный счёт — математические вычисления, осуществляемые человеком без помощи дополнительных устройств (компьютер, калькулятор, счёты и т. п.) и приспособлений (ручка, карандаш, бумага и т. п.).

Процесс устного счёта можно рассматривать как технологию счёта, объединяющую представления и навыки человека о числах, математические алгоритмы арифметики.

Имеются три вида технологии устного счёта, которые используют различные физические возможности человека:

счёт «на пальцах»;

аудиомоторная технология счёта;

визуальная технология счёта.

Характерной особенностью аудиомоторного устного счёта является сопровождение каждого действия и каждого числа словесной фразой типа «дважды два — четыре». Традиционная система счёта является именно аудиомоторной технологией. Недостатками аудиомоторного способа ведения расчётов являются:

отсутствие в запоминаемой фразе взаимосвязей с соседними результатами,

невозможность выделить во фразах о таблице умножения отдельно десятки и единицы произведения без повторения всей фразы;

невозможность обратить фразу вспять от ответа к множителям, что важно для выполнения деления с остатком;

медленная скорость воспроизведения словесной фразы.

Супервычислители, демонстрируя высокие скорости мышления, используют свои визуальные способности и отличную зрительную память. Люди, которые владеют скоростными вычислениями, не используют слов в процессе решения арифметического примера в уме. Они демонстрируют реальность визуальной технологии устного счёта, лишённой главного недостатка — замедленной скорости выполнения элементарных действий с числами.

Приемы устного счета

Чтобы умножить любое число от 1 до 9 на 9, посмотрите на руки. Загните палец, который соответствует умножаемому числу (например, 9х3 – загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9х3 – это 2), затем посчитайте после загнутого пальца (в нашем случае это 7).

Умножение чисел от 10 до 20.

Можно очень просто умножать такие числа!

К одному из чисел надо прибавить количество единиц другого, умножить на 10 и прибавить произведение единиц чисел.

Умножение на 11.

Все мы знаем, что при умножении на 10 к числу добавляется 0, а знаете ли вы, что существует такой же простой способ умножения двузначного числа на 11? Вот он:

Чтобы двузначное число, сумма цифр которого не превышает 10, умножить на 11, надо цифры этого числа раздвинуть и поставить между ними сумму этих цифр.

Вычитание из 1000.

(Представьте, что вы пришли в магазин с крупной купюрой)

Чтобы выполнить вычитание из 1000 и быстро рассчитать сдачу, можете пользоваться этим простым правилом:

— Отнимите от 9 все цифры, кроме последней.

— А последнюю цифру отнимите от 10!

Быстрое возведение в квадрат.

Этот прием поможет быстро возвести в квадрат двузначное число, которое заканчивается на 5. Умножьте первую цифру саму на себя +1, а в конце допишите 25. Вот и все!

Пример: 252= (2 ∙ (2+1)) добавляем 25

2 ∙ 3 = 6. В ответе получаем 625

Умножение на 101.

Для умножения двузначного числа на 101 надо просто записать число два раза. 34 х 101 = 3434.

Для умножения числа на 4 нужно два раза умножить его на 2. Для деления — дважды разделить на 2.

Умножать на 5 удобнее так: сначала умножить на 10, а потом разделить на 2 посередине сумму (N+A).

При умножении на 1,5 умножаемое нужно разделить пополам и прибавить к умножаемому, например 48×1,5= 48/2+48=72. Можно применить при умножении на 15 48×1,5×10 = 720.

Большинство приемов быстрого счета похоже на фокусы. Много остроумных и, главное, быстрых приемов помогают возводить число в степень, извлекать квадратный корень. Знаменитые «30 приемов Перельмана» для математически мыслящих людей будут покруче шоу Коперфильда, потому что они еще и ПОНИМАЮТ что происходит, и как оно происходит. Ну а остальные могут просто наслаждаться красивым фокусом. Например, нужно перемножить 45 на 37. Напишем числа на листе и разделим их вертикальной чертой. Левое число делим на 2, отбрасывая остаток, пока не получим единицу. Правое — умножаем до тех пор, пока число строчек в столбике не сравняется. Затем вычеркиваем из ПРАВОГО столбика все те числа, напротив которых в ЛЕВОМ столбике получился четный результат. Оставшиеся числа из правого столбика складываем. Получится 1665. Перемножьте числа привычным способом. Ответ сойдется.

1.2 Соревнования по устному счёту

В настоящее время в прибалтийских странах, Словении и Украине проводятся соревнования по устному счёту среди школьников под названием Пранглимине (эст. Pranglimine ). Начиная с 2004 года проводятся международные соревнования среди школьников и взрослых. В 2016 году соревнования прошли в Мурска-Собота (Словения).

Начиная с 2004 года, один раз в два года проводится Мировой чемпионат по вычислениям в уме. Соревнования проводятся по решению таких задач, как сложение десяти 10-значных чисел (по правилам 2016 года даётся 7 минут на это задание), умножение двух 8-значных чисел за 10 минут, расчёт дня недели по григорианскому календарю по заданной дате с 1600 по 2100 годы (1 минута), корень квадратный из 6-значного числа за 10 минут (результат должен быть представлен с точностью до 8 знаков после запятой). Также определяется победитель в категории «Лучший универсальный счётчик» по итогам решения шести неизвестных «задач с сюрпризом». К заявке на участие прикладываются результаты в интеллектуальных видах спорта и результат в программах Memoriad, подтверждёные кем-то (например, учителем математики). Ограничения по возрасту нет, не делается также различий между полами. Участник начинает выполнение каждого задания с команды «Нейроны готовсь, пошли» (Neurons: On the ready, go). Чемпионат в 2018 году прошёл 28—30 сентября 2018 года в Научном центре Phæno в Вольфсбурге, Германия по таким правилам.

Memoriad (MEntal math + meMORy + olimpIAD) — международная олимпиада по устному счёту, запоминанию и скорочтению, проводится раз в 4 года (совпадает по годам с летними Олимпийскими играми). Среди заданий по устному счёту: умножение 5-, 8- и 20-значных чисел, деление 10-значных чисел на 5-значные, извлечение квадратного корня из 6-, 8- и 10-значного числа, сложение 250 двухзначных чисел с показом каждого числа 0,6 секунды. Среди других заданий: запоминание бинарных чисел, десятичных чисел за определённое время (от 1 минуты до 1 часа).

1.3 Устный счёт в искусстве

В России хорошо известна картина русского художника Николая Богданова-Бельского « Устный счёт в народной школе С. А. Рачинского » (рис.7), написанная в 1895 году. Приведённая на доске задача, над которой размышляют ученики, требует достаточно высоких навыков устного счёта и смекалки.

Феномен быстрого счёта больного аутизмом раскрывается в фильме « Человек дождя » (рис. 5) Барри Левинсона и в фильме « Пи » (рис. 3) Даррена Аронофски . Барри Левинсон (рис. 4) ( англ. Barry Levinson; род. 6 апреля 1942 ) — американский кинорежиссёр, сценарист и продюсер. Лауреат премии «Оскар» 1989 года .

Да́ррен Ароно́фски ( англ. Darren Aronofsky; род. 12 февраля 1969 , Бруклин , Нью-Йорк , США ) — американский кинорежиссёр , сценарист и продюсер (рис. 6).

Приемы быстрого счета способны здорово облегчить жизнь и ребенку в школе, и маме в магазине или на кухне, и папе на производстве или в офисе. Самый простой способ тренировки и, одновременно, разминки мозга: устный счет вслух (обязательно!) через число до ста и обратно. Утром, стоя под душем, или готовя завтрак, посчитайте: 2.. 4.. 6.. 100. 98.. 96. Можно считать через три, через восемь — главное, делать это вслух. Всего через пару недель регулярных занятий вы удивитесь, насколько ПРОЩЕ станет обращаться с числами. Знания математики нужны всем – и ученикам, и учителям. Способ устного выполнения математических действий влияет на качество (наличие или отсутствие ошибок при вычислении). Также способ выполнения влияет на время проведения расчетов: знание определенных трюков для быстрого вычисления, конечно же, сокращает время выполнения задания.

Источник