Способы упрощения логических выражений
Тема 3. Основы математической логики 1. Логические выражения и логические операции.
2. Построение таблиц истинности и логических функций.
3. Законы логики и преобразование логических выражений.
Лабораторная работа № 3. Основы математической логики.
3. Законы логики и правила преобразования логических выражений
Закон двойного отрицания (двойное отрицание исключает отрицание):
А =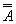 
.
Переместительный (коммутативный) закон:
для логического сложения: А Ú B = B Ú A;
Результат операции над высказываниями не зависит от того, в каком порядке берутся эти высказывания.
Сочетательный (ассоциативный) закон:
для логического сложения: (А Ú B) Ú C = A Ú (B Ú C);
для логического умножения:(A & B) & C = A & (B & C).
При одинаковых знаках скобки можно ставить произвольно или вообще опускать.
Распределительный (дистрибутивный) закон:
для логического умножения:(A & B) Ú C = (A Ú C) & (B Ú C).
Закон определяет правило выноса общего высказывания за скобку.
Закон общей инверсии (законы де Моргана):
для логического сложения: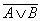 
= 
& 
;
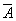
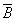
для логического умножения: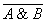 
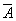
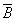
= Ú
Закон идемпотентности (от латинских слов idem — тот же самый и potens — сильный; дословно — равносильный):
для логического сложения: А Ú A = A;
для логического умножения:A & A = A.
Закон означает отсутствие показателей степени.
для логического умножения:A & 1 = A, A & 0 = 0.
A & 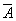= 0.
Невозможно, чтобы противоречащие высказывания были одновременно истинными.
A Ú 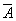= 1.
Из двух противоречащих высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.
для логического умножения:A & (A Ú B) = A.
Знание законов логики позволяет проверять правильность рассуждений и доказательств. Основываясь на законах, можно выполнять упрощение сложных логических выражений. Такой процесс замены сложной логической функции более простой, но равносильной ей, называется минимизацией функции.
Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т.п.), другие — основаны на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, де Моргана и др.).
Нарушения законов логики приводят к логическим ошибкам и вытекающим из них противоречиям.
Пример 1. Упростить формулу (А Ú В) & (А Ú С).
A Ú B & A Ú B & C = A & (1 Ú B) Ú B & C = A Ú B & C.
Таким образом, мы доказали закон дистрибутивности.
Всякую формулу можно преобразовать так, что в ней не будет отрицаний сложных высказываний — все отрицания будут применяться только к простым высказываниям.
Пример 2. Упростить выражения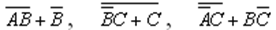 
так, чтобы в полученных формулах не содержалось отрицания сложных высказываний.
Решение:
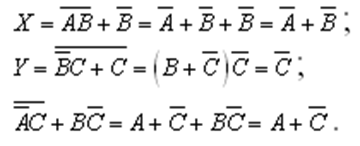
Источник
Урок 11
Упрощение логических выражений
§21. Упрощение логических выражений
Содержание урока
Законы алгебры логики
Законы алгебры логики
Для упрощения логических выражений используют законы алгебры логики. Они формулируются для базовых логических операций — «НЕ», «И» и «ИЛИ».
Закон двойного отрицания означает, что операция «НЕ» обратима: если применить ее два раза, логическое значение не изменится. Закон исключённого третьего основан на том, что в классической (двузначной) логике любое логическое выражение либо истинно, либо ложно («третьего не дано»). Поэтому если А = 1, то А = 0 (и наоборот), так что произведение этих величин всегда равно нулю, а сумма — единице.
Операции с константами и закон повторения легко проверяются по таблицам истинности операций «И» и «ИЛИ». Переместительный и сочетательный законы выглядят вполне привычно, так же, как и в арифметике. Почти везде «работает» аналогия с алгеброй чисел, нужно только помнить, что в логике 1 + 1 = 1, а не 2.
Распределительный закон для операции «ИЛИ» — это обычное раскрытие скобок. А вот для операции «И» мы видим незнакомое выражение, в алгебре чисел это равенство неверно. Доказательство можно начать с правой части, раскрыв скобки:
(А + В) • (А + С) = А • А + А • С + В • А + В • С.
Дальше используем закон повторения (А • А = А) и заметим, что
А + А • С = А • (1 + С) = А • 1 = А.
Аналогично доказываем, что А + В • А = А • (1 + В) = А, таким образом,
(А + В) • (А + С) = А + В • С.
Равенство доказано. Попутно мы доказали также и закон поглощения для операции «И» (для операции «ИЛИ» вы можете сделать это самостоятельно). Отметим, что из распределительного закона следует полезное тождество:
А + А • В = (А + А ) • (А + В) = А + В.
Правила, позволяющие раскрывать отрицание сложных выражений, названы в честь шотландского математика и логика Огастеса (Августа) де Моргана. Обратите внимание, что при этом не просто «общее» отрицание переходит на отдельные выражения, но и операция «И» заменяется на «ИЛИ» (и наоборот). Доказать законы де Моргана можно с помощью таблиц истинности.
Теперь с помощью приведённых законов алгебры логики упростим полученное ранее логическое выражение для объединения областей 3 и 4 на диаграмме с тремя переменными (§ 20, рис. 3.15):
(А • В • C ) + А • В • C = (А + А ) • В • C = В • C .
Здесь мы сначала вынесли общий множитель двух слагаемых за скобки, а затем применили закон исключённого третьего.
В общем случае можно рекомендовать такую последовательность действий.
1. Заменить все «небазовые» операции (исключающее ИЛИ, импликацию, эквивалентность и др.) на их выражения через базовые операции «НЕ», «И» и «ИЛИ».
2. Раскрыть отрицания сложных выражений по законам де Моргана так, чтобы операции отрицания остались только у отдельных переменных.
3. Используя вынесение общих множителей за скобки, раскрытие скобок и другие законы алгебры логики, упростить выражение.
(А + B ) • ( А + B ) • ( А + С)=(А + B ) • А • B • ( А + C = (А • А + B • А ) • B • ( А + С) = B • А • B • ( А + С) = А • B • B • ( А + С) = B • А • ( А + С) = B • ( А .
Здесь последовательно использованы закон де Моргана, распределительный закон, закон исключённого третьего, переместительный закон, закон повторения, снова переместительный закон и закон поглощения.
Следующая страница 
Логические уравнения
Cкачать материалы урока
Источник
Упрощение логических выражений
Основная образовательная задача урока – научить учащихся умению упрощать логические выражения, правильно определять порядок выполнения операций в логическом выражении, устанавливать связи между различными частями сложных логических выражений, умение выбирать лучший вариант решения.
Под упрощением формулы, не содержащей операций импликации и эквиваленции, понимают равносильное преобразование, приводящее к формуле, которая либо содержит по сравнению с исходной меньшее число операций конъюнкции и дизъюнкции и не содержит отрицаний неэлементарных формул, либо содержит меньшее число вхождений переменных.
Обозначим: X – логическое высказывание, 
– инверсия, & – конъюнкция, 
– дизъюнкция, 
– импликация, 
– эквиваленция.
Применение основных законов логики для упрощения логических выражений.
Представленные примеры демонстрируют основные приемы упрощения логических выражений.
Упростить логическое выражение:
1) 
Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций:
Воспользуемся распределительным законом и вынесем за скобки общий множитель, затем операцией переменной с ее инверсией.
Воспользуемся распределительным законом и вынесем за скобки общий множитель, затем операцией переменной с ее инверсией, затем операцией с константами.
2) 
Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций. В выражении присутствуют два выражения в скобках, соединенных дизъюнкцией. Сначала преобразуем выражения в скобках.
В первой скобке воспользуемся распределительным законом, во второй скобке – раскроем инверсию по правилу де Моргана и избавимся от инверсии по закону двойного отрицания.
Воспользуемся операцией переменной с ее инверсией.
3) 
Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций. В выражении присутствуют два выражения в скобках, соединенных конъюнкцией. Сначала преобразуем выражения в скобках.
Раскроем инверсию по правилу де Моргана, избавимся от инверсии по закону двойного отрицания.
Воспользуемся переместительным законом и поменяем порядок логических сомножителей.
Применим закон склеивания 
Воспользуемся распределительным законом, затем операцией переменной с ее инверсией, затем операцией с константами.
4) 
Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций.
В выражении присутствует импликация. Сначала преобразуем импликацию 
.
Воспользуемся правилом де Моргана, затем законом двойного отрицания, затем раскроем скобки.
Применим закон идемпотенции и перегруппируем логические слагаемые.
Воспользуемся распределительным законом и вынесем за скобки общий логический множитель.
Воспользуемся операцией с константами.
5) 
Рассмотрим 3 способа упрощения этого логического выражения.
1 способ. Перепишем выражение с помощью более привычных операций умножения и сложения.
Воспользуемся распределительным законом и раскроем скобки, затем операцией переменной с ее инверсией и законом идемпотенции.
Воспользуемся распределительным законом и раскроем скобки, затем операцией переменной с ее инверсией.
Воспользуемся законом идемпотенции.
2 способ. Перепишем выражение с помощью более привычных операций умножения и сложения.
Воспользуемся законом склеивания 
Воспользуемся операцией переменной с ее инверсией.
3 способ. Перепишем выражение с помощью более привычных операций умножения и сложения.
Повторим второй сомножитель 
, что разрешено законом идемпотенции.
Сгруппируем два первых и два последних сомножителя.
Воспользуемся законом склеивания 
6) 
Рассмотрим 2 способа упрощения этого логического выражения.
1 способ. Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций.
Воспользуемся распределительным законом и вынесем общий логический множитель за скобки.
2 способ. Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций.
Введем вспомогательный логический сомножитель 
Сгруппируем 1 и 4, 2 и 3 логические слагаемые. Вынесем общие логические множители за скобки.
Воспользуемся операцией с константами и операцией переменной с ее инверсией.
Получили два логических выражения:
Теперь построим таблицы истинности и посмотрим, правильно ли упрощено логическое выражение
| X | Y | Z |  |  |  |  |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 |
| X | Y | Z |  |  |  |  |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| X | Y | Z |  |  |  |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 | 1 |
| X | Y | Z |  |  |  |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 |
Как видно из сравнения таблиц истинности формулы являются равносильными.
Источник
