Способы упрощения логических функций
Тема 3. Основы математической логики 1. Логические выражения и логические операции.
2. Построение таблиц истинности и логических функций.
3. Законы логики и преобразование логических выражений.
Лабораторная работа № 3. Основы математической логики.
3. Законы логики и правила преобразования логических выражений
Закон двойного отрицания (двойное отрицание исключает отрицание):
А =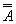 
.
Переместительный (коммутативный) закон:
для логического сложения: А Ú B = B Ú A;
Результат операции над высказываниями не зависит от того, в каком порядке берутся эти высказывания.
Сочетательный (ассоциативный) закон:
для логического сложения: (А Ú B) Ú C = A Ú (B Ú C);
для логического умножения:(A & B) & C = A & (B & C).
При одинаковых знаках скобки можно ставить произвольно или вообще опускать.
Распределительный (дистрибутивный) закон:
для логического умножения:(A & B) Ú C = (A Ú C) & (B Ú C).
Закон определяет правило выноса общего высказывания за скобку.
Закон общей инверсии (законы де Моргана):
для логического сложения: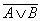 
= 
& 
;
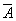
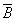
для логического умножения: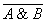 
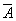
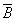
= Ú
Закон идемпотентности (от латинских слов idem — тот же самый и potens — сильный; дословно — равносильный):
для логического сложения: А Ú A = A;
для логического умножения:A & A = A.
Закон означает отсутствие показателей степени.
для логического умножения:A & 1 = A, A & 0 = 0.
A & = 0.
Невозможно, чтобы противоречащие высказывания были одновременно истинными.
A Ú 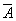= 1.
Из двух противоречащих высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.
для логического умножения:A & (A Ú B) = A.
Знание законов логики позволяет проверять правильность рассуждений и доказательств. Основываясь на законах, можно выполнять упрощение сложных логических выражений. Такой процесс замены сложной логической функции более простой, но равносильной ей, называется минимизацией функции.
Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т.п.), другие — основаны на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, де Моргана и др.).
Нарушения законов логики приводят к логическим ошибкам и вытекающим из них противоречиям.
Пример 1. Упростить формулу (А Ú В) & (А Ú С).
A Ú B & A Ú B & C = A & (1 Ú B) Ú B & C = A Ú B & C.
Таким образом, мы доказали закон дистрибутивности.
Всякую формулу можно преобразовать так, что в ней не будет отрицаний сложных высказываний — все отрицания будут применяться только к простым высказываниям.
Пример 2. Упростить выражения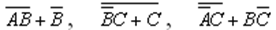 
так, чтобы в полученных формулах не содержалось отрицания сложных высказываний.
Решение:
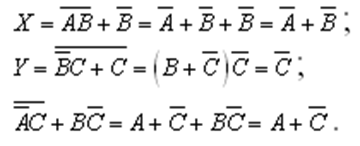
Источник
Минимизация логических функций
Минимизация логических функций
Преобразование логических функций с целью упрощения их аналитического представления называются минимизацией.
Понятие «упрощение» требует определенных договоренностей, что под этим будет пониматься. Упрощение можно рассматривать с точки зрения числа переменных в получаемоq эквивалентной функции, уменьшения количества отрицаний в результирующем выражении, более простой схемотехнической реализации при переводе получающейся ФАЛ на уровень интегральных микросхем и так далее.
Мы будем считать, что дизъюнктивная или конъюнктивная нормальная форма являются минимальными, если они содержат наименьшее суммарное число переменных среди всех ДНФ или КНФ, эквивалентных ей. При этом количество отрицаний над переменными учитывать не будем.
Методы минимизации можно разделить на несколько типов:
- Метод непосредственных преобразований логических функций.
- Метод неопределенных коэффициентов.
Аналитические методы (метод Квайна1 1 Квайн, Уиллард Ван Орман — американский философ, логик и математик , метод Квайна – Мак-Класки).
Рассмотрим их более подробно. Рассмотрение будем проводить на основе дизъюнктивных нормальных форм. Для КНФ теоретические рассуждения будут аналогичными.
В то же время, иллюстрировать соответствующие положения будем как на примерах дизъюнктивны, так и конъюнктивных форм.
Если некоторая логическая функция 
равна нулю на тех же наборах, на которых равняется нулю другая функция f, то говорят, что функция входит в функцию f. Другими словами, функция входит в функцию f тогда, когда она накрывает нулями все нули функции f, а единицы функции f могут быть накрыты как нулями, так и единицами функции .
Очевидно, что ФАЛ «Константа ноль» входит во все функции, а в ФАЛ «Константу единица» входят все функции.
Функцию , входящую в данную функцию f, называют ее импликантой.
Простыми (первичными) импликантами (имплицентами для КНФ) логической функции f называют такие элементарные произведения или элементарные суммы (для имплицент), которые сами входят в данную функцию, но никакая собственная частьэтих произведений (сумм) не входит в функцию f.
Собственной частью называют произведение, полученное путем исключения из данного произведения одного или нескольких сомножителей.
Примеры этих определений показаны в Табл. 3.1.
Источник
Упрощение логических выражений
Основная образовательная задача урока – научить учащихся умению упрощать логические выражения, правильно определять порядок выполнения операций в логическом выражении, устанавливать связи между различными частями сложных логических выражений, умение выбирать лучший вариант решения.
Под упрощением формулы, не содержащей операций импликации и эквиваленции, понимают равносильное преобразование, приводящее к формуле, которая либо содержит по сравнению с исходной меньшее число операций конъюнкции и дизъюнкции и не содержит отрицаний неэлементарных формул, либо содержит меньшее число вхождений переменных.
Обозначим: X – логическое высказывание, 
– инверсия, & – конъюнкция, 
– дизъюнкция, 
– импликация, 
– эквиваленция.
Применение основных законов логики для упрощения логических выражений.
Представленные примеры демонстрируют основные приемы упрощения логических выражений.
Упростить логическое выражение:
1) 
Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций:
Воспользуемся распределительным законом и вынесем за скобки общий множитель, затем операцией переменной с ее инверсией.
Воспользуемся распределительным законом и вынесем за скобки общий множитель, затем операцией переменной с ее инверсией, затем операцией с константами.
2) 
Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций. В выражении присутствуют два выражения в скобках, соединенных дизъюнкцией. Сначала преобразуем выражения в скобках.
В первой скобке воспользуемся распределительным законом, во второй скобке – раскроем инверсию по правилу де Моргана и избавимся от инверсии по закону двойного отрицания.
Воспользуемся операцией переменной с ее инверсией.
3) 
Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций. В выражении присутствуют два выражения в скобках, соединенных конъюнкцией. Сначала преобразуем выражения в скобках.
Раскроем инверсию по правилу де Моргана, избавимся от инверсии по закону двойного отрицания.
Воспользуемся переместительным законом и поменяем порядок логических сомножителей.
Применим закон склеивания 
Воспользуемся распределительным законом, затем операцией переменной с ее инверсией, затем операцией с константами.
4) 
Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций.
В выражении присутствует импликация. Сначала преобразуем импликацию 
.
Воспользуемся правилом де Моргана, затем законом двойного отрицания, затем раскроем скобки.
Применим закон идемпотенции и перегруппируем логические слагаемые.
Воспользуемся распределительным законом и вынесем за скобки общий логический множитель.
Воспользуемся операцией с константами.
5) 
Рассмотрим 3 способа упрощения этого логического выражения.
1 способ. Перепишем выражение с помощью более привычных операций умножения и сложения.
Воспользуемся распределительным законом и раскроем скобки, затем операцией переменной с ее инверсией и законом идемпотенции.
Воспользуемся распределительным законом и раскроем скобки, затем операцией переменной с ее инверсией.
Воспользуемся законом идемпотенции.
2 способ. Перепишем выражение с помощью более привычных операций умножения и сложения.
Воспользуемся законом склеивания 
Воспользуемся операцией переменной с ее инверсией.
3 способ. Перепишем выражение с помощью более привычных операций умножения и сложения.
Повторим второй сомножитель 
, что разрешено законом идемпотенции.
Сгруппируем два первых и два последних сомножителя.
Воспользуемся законом склеивания 
6) 
Рассмотрим 2 способа упрощения этого логического выражения.
1 способ. Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций.
Воспользуемся распределительным законом и вынесем общий логический множитель за скобки.
2 способ. Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций.
Введем вспомогательный логический сомножитель 
Сгруппируем 1 и 4, 2 и 3 логические слагаемые. Вынесем общие логические множители за скобки.
Воспользуемся операцией с константами и операцией переменной с ее инверсией.
Получили два логических выражения:
Теперь построим таблицы истинности и посмотрим, правильно ли упрощено логическое выражение
| X | Y | Z |  |  |  |  |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 |
| X | Y | Z |  |  |  |  |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| X | Y | Z |  |  |  |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 | 1 |
| X | Y | Z |  |  |  |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 |
Как видно из сравнения таблиц истинности формулы являются равносильными.
Источник
