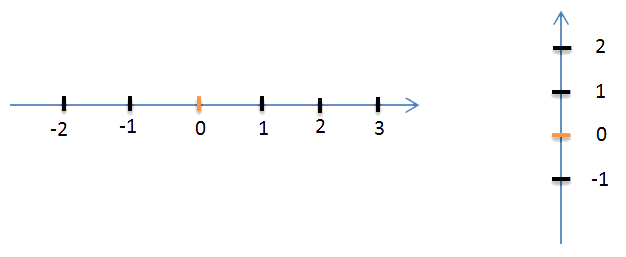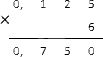Способы умножения с минусом

умножение отрицательных

Как умножать отрицательные числа!? Сколько вариантво существует умножения отрицательных. Разберем все варианты. и последним — умножим отрицательные на калькуляторе.

Умножить отрицательные в отличии от некоторых других действий с отрицательными, например сложение и вычитание существует только два варианта:

Об умножении отрицательных чисел.

Правила умножения отрицательных чисел.

Для умножения отрицательных чисел существует только два пункта в правилах «умножения отрицательных чисел» :

1.1.) Если два множителя отрицательные .

Первый пункт правил умножения звучит так : «если два множителя отрицательные, то при умножении минус на минус дает плюс, т.е. умножение двух отрицательных чисел равно умножению этих же чисел без минуса.»

1.2.) Если у множителей противоположные знаки.

Противоположные знаки у множителей — это означает, что только один множитель отрицательный.

Второй пункт правил умножения звучит так : «если из двух множителей только один отрицательный, то при умножении, минус на плюс, дает минус, т.е. у произведения знак будет отрицательным.»

Умножить отрицательные числа.

Пример умножения двух отрицательных чисел

У нас два отрицательных числа и мы их должны умножить :

У множителей два минуса, а как мы знаем из правил, минус на минус дает плюс. Значит, убираем у наших множителей два минуса.

(-12) * (-15) = 12 * 15 = 180

Умножить отрицательное и положительное число.

Рассмотрим пример умножения отрицательных чисел по второму пункту правил.

Для этого нам понадобятся цифры :

Как мы знаем из правил, в случае, если отрицательное число только одно, то результат умножения будет отрицательным:

12 * (-15) = -(12*15) = -180

Умножить отрицательные числа на калькуляторе.

Мы уже умножали два отрицательных числа, теперь сделаем умножение отрицательных чисел на калькуляторе!

Набираем первый множитель 12.

Меняем знак на отрицательный, кнопкой плюс/минус -«±».

Набираем второй множитель : 15.

Меняем знак на отрицательный, кнопкой плюс/минус : «±».

Получаем результат умножения двух отрицательных чисел.

Умножить отрицательное и положительное число на калькуляторе.

Нам осталось разобрать умножение отрицательных на калькуляторе если одно из множителей отрицательное.

Набираем первый множитель 12.

Меняем знак на отрицательный, кнопкой плюс/минус -«±».

Набираем второй множитель : 15.

Получаем результат умножения двух отрицательных чисел, где лишь один из множителей отрицательный.

Источник

Способы умножения

Все знают, как умножать в столбик, немного меньше людей знают об умножении линиями, но есть и другие интересные способы.

Умножение чисел — это очень простая операция, фактически, то же самое, что и суммирование. Конечно, пока сами числа не большие.

2х3=2+2+2 (три раза по два) или 24х6=24+24+24+24+24+24 (шесть раз по 24)

То есть, знать таблицу умножения вовсе не обязательно? Да, но с ней удобнее. Например, в случае умножения чисел 235х4596, число 4596 придется сложить 235 раз! Или наоборот, 235 сложить 4596 раз…

Слово «сложить» употреблено не зря. Вот простой способ в этом убедится. Нужно взять листок бумаги сложить его 5 раз в одном направлении, а потом 3 раза в другом. Получится действие 5х3. Считаем получившиеся от сгибания прямоугольники — их 15. Это то же самое, если бы мы взяли 3 полоски ткани (или чего угодно) длинной 5 и сложили вместе.

Как ни крути, а получается — 15!

Необычные способы умножения

В школе нас учат использовать два инструмента: таблицу Пифагора (считается что таблицу умножения придумал именно этот греческий математик) и умножению «в столбик». Это действительно самые эффективные инструменты? Кроме них есть еще несколько интересных способов умножать числа. Может, какой-то из них будет проще и учить таблицу не придется?

По-крестьянски

Использовался для определения площади земельного участка. Например, имеем поле длинной 6 и шириной 5.

Чтобы узнать, сколько будет 6х5 делаем следующее: левое число делим на 2, а правое умножаем на 2, пока от левого числа не останется единица.

2/2= 1 | 10*2=20

4х5=20, все правильно, так же как и 1х20=20

Что происходит при таком способе? Мы разделяем прямоугольник пополам, пока его ширина не станет равняться единице. Делить на два не сложно.

Вот только что будет, если одна из сторон не будет делиться на 2? Будет долгий и не такой уж простой процесс.

6/2=3 | 2*2=4 → 12

3/2=1,5 | 4*2=8 → 12

1,5/2=0,75 | 8*2=16 → 12

Если в левой части четное число — эту строку не считаем, если значение меньше единицы — тоже отбрасываем, остается вторая и третья строка, а это 8+4=12. А если представить, что умножит нужно 173 на 735? Нет, такой способ умножения не самый легкий и простой.

Можно делить/умножать и на 3, но тогда нужно знать таблицу умножения «на три», тогда уж и 5 и 7 и… Да, удобнее выучить ее всю. Также, если будет необходимо перемножить большие числа, процесс будет очень длинным.

Восточный способ

То ли китайский, то ли японский способ умножения, при помощи линий, он же «графический». Его суть состоит в том, что цифры первого числа изображаются в виде параллельных линий, а второго — перпендикулярных им. Количество пересечений и является результатом умножения. То есть, здесь знать таблицу умножения не нужно, достаточно уметь суммировать. Например, так:

2 х 3 и даже 15 х 12

Японский или китайский метод, суть не меняется

Как работает умножение линиями?

Первое число (фиолетовым цветом на картинке) рисуется так: Снизу вверх, слева на право, сначала тысячи, потом сотни, десятки, единицы. Второе число (голубым цветом на картинке) рисуется наоборот: сверху-вниз.

В первом примере все просто 2 и 3. Две линии пересекают 3 другие, получается 6 точек. Во втором, сначала рисуем 15 — единицу (один десяток), потом пять линий изображающих 5 (пять единиц). Потом (12) перпендикулярно ей вторую единицу и 2 линии.

Далее нужно посчитать пересечения, но уже в обратном направлении. Начинать справа. В примере это 10, 7 и 1. Результат складывается в столбик:

Если сравнить с традиционным «столбиком», сперва может показаться, что японско-китайский метод проще…

А что делать, если нужно умножить 10 на 12? Как изобразить «ноль» линией? Никак, он участия не принимает, можно нарисовать его пунктиром и пересечение не считать, все просто…

Но вот уже случае 853х951 рисовать и считать точки придется очень много. Старый-добрый столбик опять окажется удобнее. Каждый сам может попробовать перемножить 9878 и 8794 «японским методом» и засечь необходимое время.

Японский метод с нулем

Эта методика не универсальна, совсем не подходит, когда числа достаточно большие, зато ее очень просто объяснить маленьким детям, которые еще не знают таблицу умножения.

Жалюзи

Встречается еще и название «решетки» и индийский метод умножения. Поверить в индийское происхождение проще всего, если вспомнить, кто вообще придумывал эту вашу математику в древности. Итак, чтобы умножить два числа, нужно построить матрицу (если угодно — таблицу, мы же пытаемся быть проще).

Умножаем 45 на 82

Так как в каждом числе по 2 цифры, таблица будет 2х2. Каждую ячейку нежно перечеркнуть по диагонали. Далее записываем слева-на-право, и сверху-вниз цифры 4, 5, 8, 2 напротив каждой ячейки. Начинаем умножать цифры находящиеся напротив друг-друга. 4 на 8, 5 на 8, 4 на 2 и 5 на 2.

Ну вот опять нужна таблица умножения, иначе придется долго складывать числа.

Результаты записываются в ячейки хитрым способом, десятки над диагональю, а единицы — под ней. Но, если значение меньше 10 (то есть это одна, а не две цифры), то вместо десятки верху пишется «ноль», как при умножении 4х5. Но можно оставить поле пустым.

Теперь, чтобы узнать результат, нужно посчитать сумму в каждой диагонали, как показано на картинке. Сверху-вниз:

3

0+2+4=6

8+1=9

0

В результате получаем 3690.

Тоже достаточно просто, только с небольшими значениями, для умножения трехзначных чисел придется рисовать таблицу размером 3х3=9 ячеек.

Какой метод умножения лучше?

Если перепробовать все способы умножения чисел, становится очевидно, что все представленные альтернативные методы умножения — это все варианты знакомого «столбика». Также операции разбиваются на более мелкие: сначала умножение, потом — суммирование.

Только в так называемом китайском/японском способе умножение как таковое не используется (вместо него пересечение линий) и в этом варианте действительно можно обойтись без таблицы умножения, но придется много рисовать, что повышает вероятность совершить ошибку при пересчете точек пересечения.

Есть мнение, что популярность умножения в столбик вызвана именно компактностью записи. Так на умножение требуется меньше бумаги, меньше чернил (да, чернила раньше использовались и тоже стоили денег) и соответственно времени.

Знать нетрадиционные методики интересно и даже полезно, но школьная таблица умножения, все же быстрее, а если вы знаете как умножать в столбик — это удобнее, чем любой другой способ. Если, конечно, не считать калькулятор.

Источник

Умножение отрицательных чисел

Используя понятие модуля числа, сформулируем правила умножения положительных и отрицательных чисел.

Умножение чисел с одинаковыми знаками

Первый случай, который может вам встретиться — это умножение чисел с одинаковыми знаками.

Чтобы умножить два числа с одинаковыми знаками надо:

• перемножить модули чисел;
• перед полученным произведением поставить знак « + » (при записи ответа знак «плюс» перед первым числом слева можно опускать).

Примеры умножения отрицательных и положительных чисел.

Умножение чисел с разными знаками

Второй возможный случай — это умножение чисел с разными знаками.

Чтобы умножить два числа с разными знаками, надо:

• перемножить модули чисел;
• перед полученным произведением поставить знак « − ».

Примеры умножения отрицательных и положительных чисел.

Правила знаков для умножения

Запомнить правило знаков для умножения очень просто. Данное правило совпадает с правилом раскрытия скобок.

Минус на минус даёт плюс,

Плюс на минус даёт минус.

В «длинных» примерах, в которых есть только действие умножение, знак произведения можно определять по количеству отрицательных множителей.

При чётном числе отрицательных множителей результат будет положительным, а при нечётном количестве — отрицательным.

В примере пять отрицательных множителей. Значит, знак результата будет «минус».

Теперь вычислим произведение модулей, не обращая внимание на знаки.

Конечный результат умножения исходных чисел будет:

Умножение на ноль и единицу

Если среди множителей есть число ноль или положительная единица, то умножение выполняется по известным правилам.

Особую роль при умножении рациональных чисел играет отрицательная единица « −1 ».

При умножении на « −1 » число меняется на противоположное.

В буквенном выражении это свойство можно записать:

При совместном выполнении сложения, вычитания и умножения рациональных чисел сохраняется порядок действий, установленный для положительных чисел и нуля.

Пример умножения отрицательных и положительных чисел.

Источник

Как умножать отрицательные числа

О чем эта статья:

Основные определения

Вспомним, как отличить положительное число от отрицательного, что такое умножение и какие у него свойства.

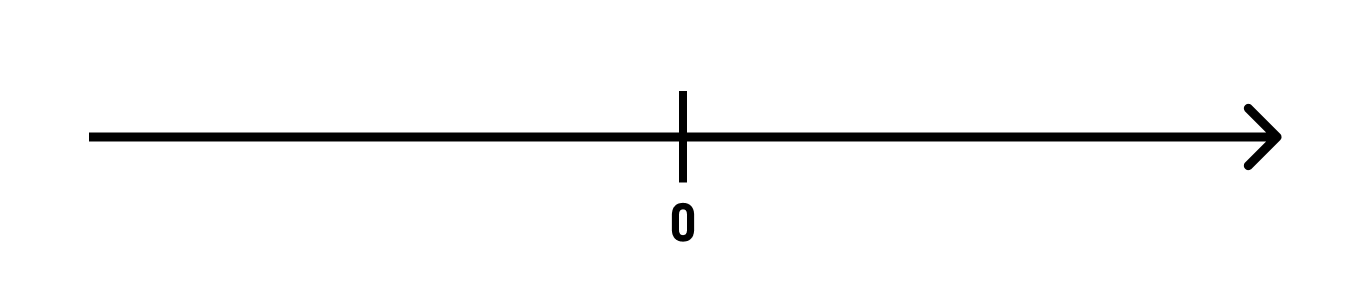
Начнем с того, что проведем прямую и отметим на ней начало отсчета — точку нуль (0). А теперь укажем направление движения по прямой вправо от начала координат. В этом нам поможет красивая стрелка:

Два главных определения:

Положительные числа — это точки координатной прямой, которые лежат правее начала отсчета (нуля). Иногда рядом с ними ставят знак плюс — «+», но чаще всего положительные числа никак не обозначают. То есть «+1» и «1» — это одно и тоже число.

Отрицательные числа — это точки координатной прямой, которые лежат левее начала отсчета (нуля). Их всегда обозначают знаком минус — «-».

Нуль (0) — ни положительное, ни отрицательное число. Вот это ему повезло!

Числовую ось можно расположить как горизонтально (стрелка вверх), так и вертикально (стрелка вправо).

Если стрелка направлена вверх, то в верхней части от начала отсчета всегда расположены положительные числа, а в нижней — отрицательные. Смотрите:

Прямая, на которой отмечена начальная точка, положительное направление и единичный отрезок, называется координатной или числовой осью.

Умножение — арифметическое действие в котором участвуют два аргумента. Один множимый, второй множитель. Результат их умножения называется произведением.

1. От перестановки множителей местами произведение не меняется.
   a * b = b * a
2. Результат произведения трёх и более множителей не изменится, если любую группу заменить произведением.
   a * b * c = (a * b) * c = a * (b * c)

Вычислять можно в уме, при помощи таблицы умножения или в столбик. Продвинутые школьники могут использовать онлайн-калькулятор.

Умножение отрицательных чисел

Правило умножения отрицательных чисел: чтобы умножить два отрицательных числа, нужно перемножить их модули. Это значит, что для любых отрицательных чисел -a, -b верно равенство:

А вот как умножить два числа с разными знаками:

• перемножить модули этих чисел
• перед полученным числом поставить знак минус

А теперь упростим правила. Сформулируем их в легкой форме с минимумом слов, чтобы проще запомнить:

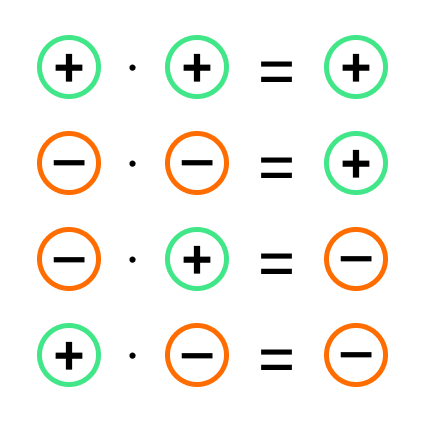
• «—» — при умножении минус на минус ответ будет положительным
  или минус на минус дает плюс
• «-+» — при умножении минуса на плюс ответ будет отрицательным
  или минус на плюс дает минус
• «+-» — при умножении плюса на минус ответ будет отрицательным
  или плюс на минус дает минус
• «++» — при умножении плюса на плюс ответ будет положительным
  или плюс на плюс дает плюс.

Примеры умножения отрицательных чисел

Пример 1. Вычислить: (-2)∗(-2) и (-3)∗(-7)

Вспомним правило: отрицательное число умножить на отрицательное — получается ответ со знаком плюс. Считаем:

Пример 2. Вычислить: (-11)∗11 и (-20)∗2

Вспомним правило: отрицательное число умножить на положительное — получается ответ со знаком минус. Считаем:

Пример 3. Вычислить произведение: 5∗(-5) и 12∗(-8)

Вспомним правило: умножение положительного на отрицательное число дает отрицательный результат. Считаем:

Пример 4. Вычислить произведение: (-0,125 ) * (-6)

1. Используем правило умножения отрицательных чисел:
   (-0,125 ) * (-6) = 0,125 * 6.
2. Выполним умножение десятичной дроби на натуральное число столбиком:
   

Источник