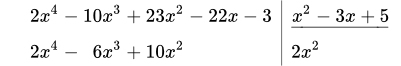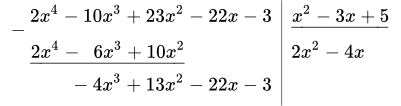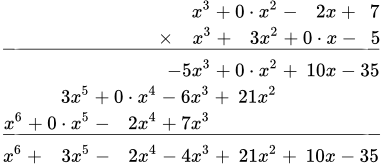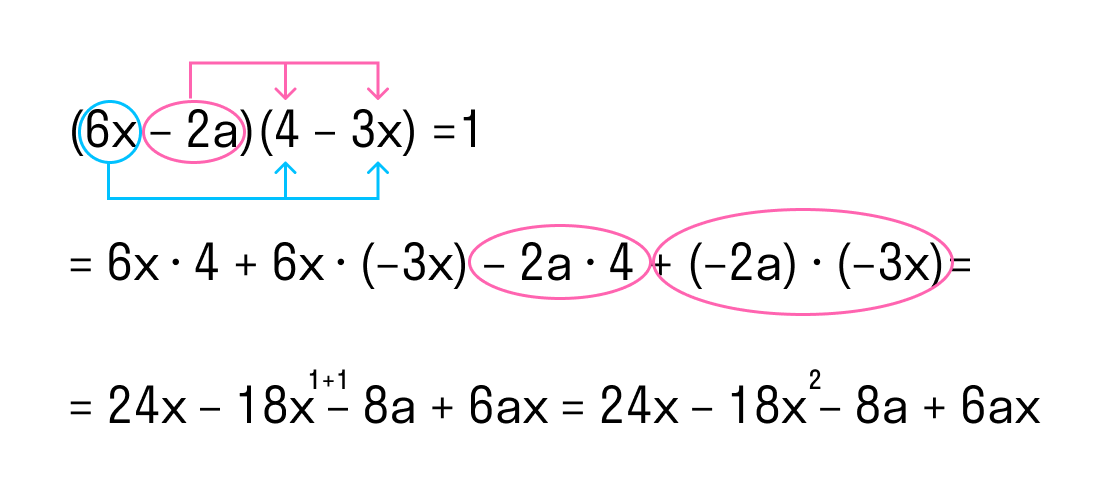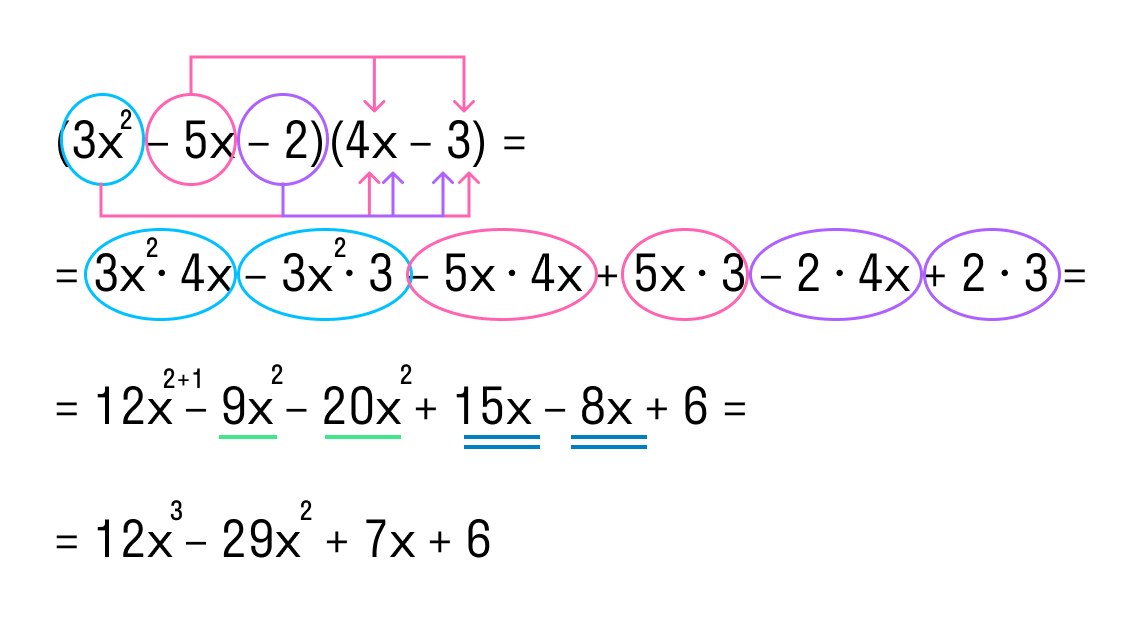Способы умножения многочленов столбиком

Деление и умножение многочленов уголком и столбиком

Теорема

Пусть P_k ( x ) , Q_n ( x ) – многочлены от переменной x степеней k и n , соответственно, причем k ≥ n . Тогда многочлен P_k ( x ) можно представить единственным способом в следующем виде:
(1) P_k ( x ) = S_k–n ( x ) Q_n ( x ) + U_{n– 1} ( x ) ,
где S_k–n ( x ) – многочлен степени k–n , U_{n– 1} ( x ) – многочлен степени не выше n– 1 , или нуль.

Доказательство

По определению многочлена:
;
;
;
,
где p_i , q_i – известные коэффициенты, s_i , u_i – неизвестные коэффициенты.

Введем обозначение:
.
Подставим в (1) :
;
(2) .
Первый член в правой части – это многочлен степени k . Сумма второго и третьего членов – это многочлен степени не выше k – 1 . Приравняем коэффициенты при x k :
p_k = s_k-n q_n .
Отсюда s_k-n = p_k / q_n .

Преобразуем уравнение (2):
.
Введем обозначение: .
Поскольку s_k-n = p_k / q_n , то коэффициент при x k равен нулю. Поэтому – это многочлен степени не выше k – 1 , . Тогда предыдущее уравнение можно переписать в виде:
(3) .

Это уравнение имеет тот же вид, что и уравнение (1), только значение k стало на 1 меньше. Повторяя эту процедуру k–n раз, получаем уравнение:
,
из которого определяем коэффициенты многочлена U_{n– 1} ( x ) .

Итак, мы определили все неизвестные коэффициенты s_i , u_l . Причем s_k–n ≠ 0 . Лемма доказана.

Деление многочленов

Разделив обе части уравнения (1) на Q_n ( x ) , получим:
(4) .
По аналогии с десятичными числами, S_k–n ( x ) называется целой частью дроби или частным, U_{n– 1} ( x ) – остатком от деления. Дробь многочленов, у которой степень многочлена в числителе меньше степени многочлена в знаменателе называется правильной дробью. Дробь многочленов, у которой степень многочлена в числителе больше или равна степени многочлена в знаменателе называется неправильной дробью.

Уравнение (4) показывает, что любую неправильную дробь многочленов можно упростить, представив ее в виде суммы целой части и правильной дроби.

Деление многочленов уголком

По своей сути, целые десятичные числа являются многочленами, у которых переменная равна числу 10 . Например, возьмем число 265847. Его можно представить в виде:
.
То есть это многочлен пятой степени от 10 . Цифры 2, 6, 5, 8, 4, 7 являются коэффициентами разложения числа по степеням числа 10.

Поэтому к многочленам можно применить правило деления уголком (иногда его называют делением в столбик), применяемое к делению чисел. Единственное отличие заключается в том, что, при делении многочленов, не нужно переводить числа больше девяти в старшие разряды. Рассмотрим процесс деления многочленов уголком на конкретных примерах.

Пример деления многочленов уголком

Выделить целую часть дроби и найти остаток от деления:
.

Здесь в числителе стоит многочлен четвертой степени. В знаменателе – многочлен второй степени. Поскольку 4 ≥ 2 , то дробь неправильная. Выделим целую часть, разделив многочлены уголком (в столбик):

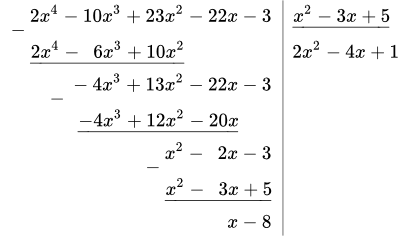
Приведем подробное описание процесса деления. Исходные многочлены записываем в левый и правый столбики. Под многочленом знаменателя, в правом столбике, проводим горизонтальную черту (уголок). Ниже этой черты, под уголком, будет целая часть дроби.

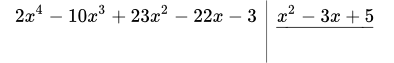
1.1 Находим первый член целой части (под уголком). Для этого разделим старший член числителя на старший член знаменателя: .

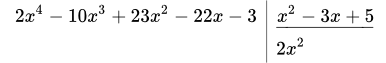
1.2 Умножаем 2 x 2 на x 2 – 3 x + 5 :
. Результат записываем в левый столбик:

1.3 Берем разность многочленов в левом столбике:

.

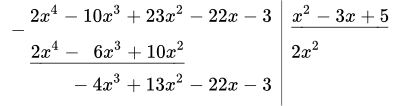
Итак, мы получили промежуточный результат:
.

Дробь в правой части неправильная, поскольку степень многочлена в числителе ( 3 ) больше или равна степени многочлена в знаменателе ( 2 ). Повторяем вычисления. Только теперь числитель дроби находится в последней строке левого столбика.
2.1 Разделим старший член числителя на старший член знаменателя: ;

2.2 Умножаем на знаменатель: ;

2.3 И вычитаем из последней строки левого столбика: ;

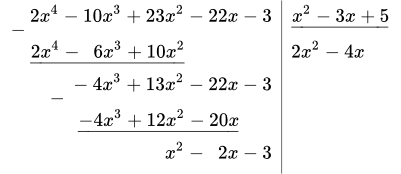
Промежуточный результат:
.

Снова повторяем вычисления, поскольку в правой части стоит неправильная дробь.
3.1 ;
3.2 ;
3.3 ;

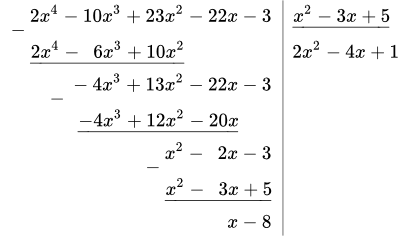
Итак, мы получили:
.
Степень многочлена в числителе правой дроби меньше степени многочлена знаменателя, 1 . Поэтому дробь – правильная.

;
2 x 2 – 4 x + 1 – это целая часть;
x – 8 – остаток от деления.

Пример 2

Выделить целую часть дроби и найти остаток от деления:
.

Выполняем те же действия, что и в предыдущем примере:

Здесь остаток от деления равен нулю:
.

Умножение многочленов столбиком

Также можно умножать многочлены столбиком, аналогично умножению целых чисел. Рассмотрим конкретные примеры.

Пример умножения многочленов столбиком

Найти произведение многочленов:
.

Умножаем многочлены столбиком.

1 Записываем исходные многочлены друг под другом в столбик и проводим черту.

2.1 Умножаем младший член второго многочлена на первый многочлен:
.
Результат записываем в столбик.

2.2 Умножаем следующий член второго многочлена на первый многочлен:
.
Результат записываем в столбик, выравнивая степени x .

2.3 Умножаем следующий (старший) член второго многочлена на первый многочлен:
.
Результат записываем в столбик, выравнивая степени x .

3 После того, как все члены второго многочлена умножили на первый, проводим черту и складываем члены с одинаковыми степенями x :
;
;
;
.

Заметим, что можно было записывать только коэффициенты, а степени переменной x можно было опустить. Тогда умножение столбиком многочленов будет выглядеть так:

Пример 2

Найти произведение многочленов столбиком:
.

При умножении многочленов столбиком важно записывать одинаковые степени переменной x друг под другом. Если некоторые степени x пропущены, то их следует записывать явно, умножив на нуль, либо оставлять пробелы.

В этом примере некоторые степени пропущены. Поэтому запишем их явно, умноженными на нуль:
.
Умножаем многочлены столбиком.

1 Записываем исходные многочлены друг под другом в столбик и проводим черту.

2.1 Умножаем младший член второго многочлена на первый многочлен:
.
Результат записываем в столбик.

2.2 Следующий член второго многочлена равен нулю. Поэтому его произведение на первый многочлен также равно нулю. Нулевую строку можно не записывать.

2.3 Умножаем следующий член второго многочлена на первый многочлен:
.
Результат записываем в столбик, выравнивая степени x .

2.3 Умножаем следующий (старший) член второго многочлена на первый многочлен:
.
Результат записываем в столбик, выравнивая степени x .

3 После того, как все члены второго многочлена умножили на первый, проводим черту и складываем члены с одинаковыми степенями x :
.

Автор: Олег Одинцов . Опубликовано: 21-05-2015

Источник

Умножение многочлена на многочлен

Что такое многочлен?

Многочленом называется алгебраическое выражение, представляющее сумму нескольких одночленов. В свою очередь, одночлены, составляющие многочлен, называются членами многочлена.

Примеры многочленов: a – 3b 2 + c; 2x + 6y; 6 – 3ac

Любой многочлен состоит из нескольких одночленов.

Так, например, многочлен 2a 2 b + 4ac – 6xy + 8 состоит из следующих одночленов:

• 2a 2 b — первый одночлен;
• 4ac — второй одночлен;
• 6xy — третий одночлен;
• 8 — четвертый одночлен.

По правилу знаков любой многочлен можно представить как сумму одночленов:

2a 2 b + 4ac – 6xy + 8 = 2a 2 b + 4ac + (-6xy) + 8

Любой знак, будь то минус или плюс, стоящий слева от одночлена, относится к его числовому коэффициенту. Соответственно, минус относится к коэффициенту 6 (то есть -6).

Как умножить многочлен на многочлен?

Для операции умножения многочлена на многочлен необходимо:

1. каждый одночлен первого многочлена умножить на каждый одночлен второго многочлена;
2. сложить полученные произведения.

Рассмотрим правило на конкретном примере.

Следует произвести умножение многочленов: (6y – 2b) * (4 – 3y).

Для этого последовательно умножим первый одночлен 6y, находящийся в первой скобке, на многочлены во второй скобке. После этого сделаем то же самое и со вторым одночленом -2b из первой скобки. При раскрытии скобок и решении примера важно помнить и соблюдать правило знаков:

(6y – 2b) * (4 – 3y) = 6y * 4 + 6y * (-3y) – 2b * 4 + (-2b) * (-3y) = 24y – 18y 1+1 – 8b + 6by = 24y – 18y 2 – 8b + 6by

Результатом умножения многочлена на многочлен так же всегда будет многочлен.

Примеры перемножения многочленов:

• (x – y) (-x – 2) = x · (-x) – 2x + xy + 2y = −x 2 – 2x + xy + 2y

• (x 2 + xy + y 2 )(x − y) = x 2 x − x 2 · y + xy · x − xy · y + y 2 · x − y 2 · y = x 2 + 1− x 2 y + x 1 + 1y − xy 1 + 1 + y 2 x − y 2 + 1= x 3 − x 2 y + x 2 y − xy 2 + xy 2 − y 3 = x 3 − y 3

Если требуется перемножить более двух многочленов? Какие правила следует помнить при выполнении этой операции?

Умножение более двух многочленов

Для операции перемножения более двух многочленов необходимо:

1. перемножить первые два многочлена между собой, записать получившийся результат в скобки;
2. умножить полученный новый многочлен на следующий многочлен;
3. выполнять предыдущие действия последовательно согласно количеству многочленов.

Рассмотрим правило на конкретном примере.

Следует произвести умножение трех многочленов:

(a – 2) (3a + 1) (4a – 3)

1. Умножаем первый многочлен на второй, полученный результат записываем в скобки:

(a – 2) (3a + 1) (4a – 3) = (a · 3a + a · 1 – 2 · 3a – 2 · 1) ( 4a − 3) =

= (3a 1+1 + a – 6a – 2) (4a – 3) = (3a 2 – 5a – 2) (4a – 3)

1. Перемножаем полученный многочлен с третьим многочленом. В конце операции приводим подобные одночлены.

(3a 2 – 5a – 2) (4a – 3) = 3a 2 · 4a – 3a 2 · 3 – 5a · 4a + 5a · 3 – 2 · 4a + 2 · 3 =

= 12a 2+1 – 9a 2 – 20a 2 + 15a – 8a + 6 =

= 12a 3 – 29a 2 + 7a + 6

Подробнее с этой темой вы сможете ознакомиться в учебнике Алгебра. 7 класс.

Источник

Умножение многочлена на многочлен

О чем эта статья:

Определение многочлена

Прежде чем мы расскажем, как умножить один многочлен на другой многочлен, разберемся в основных понятиях.

Одночлен — это произведение чисел, переменных и степеней.

Многочлен— алгебраическое выражение, которое представляет из себя сумму или разность нескольких одночленов.

Стандартный вид многочлена — представление многочлена в виде суммы одночленов стандартного вида, среди которых нет подобных одночленов.

Как привести многочлен к стандартному виду:

1. Привести к стандартному виду все одночлены, которые входят в многочлен.
2. Привести подобные члены.

Вспомним, как умножать многочлен на одночлен, двучлен на двучлен, трехчлен на трехчлен:

Правило умножения двучленов:

(a + b) * (c + d) = ac + ad + bc + bd.

Правило умножения двучлена на трехчлен:

(a + b + c) * (x + y) = ax + bx + cx + ay + by + cy.

Правило перемножения трехчленов:

(a + b + c) 2 = a 2 + b 2 + c 2 + 2ab + 2ac + 2bc.

Эти правила можно описать так: чтобы умножить один многочлен на другой, нужно каждый член первого умножить на каждый член второго многочлена. Затем полученные произведения сложить и привести результат к многочлену стандартного вида, если это возможно.

Правило умножения многочлена на многочлен

Рассмотрим пример, а после решения сформулируем правило умножения многочлена на многочлен:

• Возьмем два многочлена (a + b) и (c + d) и выполним их умножение.
• Сначала составим их произведение: (a + b)(c + d).
• Теперь обозначим (c + d) как x. После этой замены произведение примет вид: (a + b)x.
• Выполним умножение многочлена на одночлен: (a + b)x = ax + bx.
• Проведем обратную замену x на (c + d):
  a(c + d) + b(c + d). Преобразуем: ac + ad + bc + bd.
• Как изменилось произведение исходных многочленов:
  (a + b)(c + d) = ac + ad + bc + bd.
  Как раз так и выглядит формула умножения многочлена на многочлен.

Правило умножения многочлена на многочлен

Чтобы умножить многочлен на многочлен, надо каждый член первого многочлена умножить на каждый член второго многочлена и все полученные произведения сложить.

Алгоритм умножения многочлена на многочлен:

1. Первый член первого многочлена умножить на каждый член второго многочлена. Второй член первого многочлена умножить на каждый член второго многочлена. И так далее.
2. Сложить полученные произведения.
3. Преобразовать полученную сумму в многочлен стандартного вида.

Рассмотрим пример умножения многочлена на многочлен:
(6x – 2a) * (4 – 3x).

• Умножим последовательно первый одночлен 6x из первой скобки на оба одночлена второй скобки.
• Уумножим второй одночлен −2a первой скобки на оба одночлена второй скобки.

Ответ: (6x – 2a) * (4 – 3x) = 24x – 18x 2 – 8a + 6ax.

Рассмотрим пример умножения трех многочленов:
(x – 2) * (3x + 1) * (4x – 3).

• Умножим первый многочлен на второй. Результат запишем в скобках.
  
• Перемножим получившийся многочлен и третий многочлен. Приведем подобные одночлены.
  

Ответ: (x – 2) * (3x + 1) * (4x – 3) = 12x 3 – 29x 2 + 7x + 6.

Теперь мы знаем все из темы умножения многочлена на многочлен. Осталось отточить на практике новый навык и ловить хорошие и отличные отметки на контрольных.

Примеры умножения многочлена на многочлен

Рассмотрим еще несколько примеров, чтобы закрепить пройденный материал.

Пример 1. Выполнить умножение многочленов:
2 − 3x и x 2 − 7x + 1.

Запишем произведение: (2 − 3x)(x 2 − 7x + 1).

Составим сумму произведений каждого члена многочлена (2 − 3x) на каждый член многочлена (x 2 − 7x + 1). Для этого первый член первого многочлена «2» умножим на каждый член второго многочлена: 2x 2 , 2(−7x) и 2*1.

Теперь второй член первого многочлена «−3x» умножим на каждый член второго многочлена: −3xx 2 , −3x(−7x) и −3x*1.

Из полученных выражений составим сумму: 2x 2 + 2(−7x) + 2*1 − 3xx 2 − 3x(−7x) − 3x*1.

Чтобы убедиться, что мы все сделали правильно, посчитаем количество членов в полученной сумме. Их шесть. Так и должно быть, так как исходные многочлены состоят из 2 и 3 членов: 2 * 3 = 6.

Осталось полученную сумму преобразовать в многочлен стандартного вида:

2x 2 + 2(−7x) + 2*1 − 3xx 2 − 3x(−7x) − 3x*1 = 2x 2 − 14 x + 2 − 3x 3 + 21x 2 − 3x = (2x 2 + 21x 2 ) + (−14x − 3x) + 2 − 3x 3 = 23x 2 − 17x + 2 − 3x 3 .

Получается, что (2 − 3x)(x 2 − 7x + 1) = 23x 2 − 17x + 2 − 3x 3 .

Ответ: (2 − 3x)(x 2 − 7x + 1) = 23x 2 − 17x + 2 − 3x 3 .

Пример 2. Найти произведение трех многочленов:
x 2 + xy − 1, x + y и 2y − 3.

Запишем их произведение: (x 2 + xy − 1)(x + y)(2y − 3).

Умножим первые два многочлена:

(x 2 + xy − 1)(x + y) = x 2 x + x 2 y + xyx + xyy − 1x − 1y = x 3 + 2x 2 y + xy 2 − x − y.

Таким образом: (x 2 + xy − 1)(x + y)(2y − 3) = (x 3 + 2x 2 y + xy 2 − x − y)(2y − 3).

Снова выполним умножение двух многочленов:

(x 3 + 2x 2 y + xy 2 − x − y)(2y − 3) = x 3 2y + x 3 (−3) + 2x 2 y 2 y + 2x 2 y(−3) + xy 2 2y + xy 2 (−3) − x 2 y − x(−3) − y 2 y − y(−3) = 2x 3 y − 3x 3 + 4x 2 y 2 − 6x 2 y + 2xy 3 − 3xy 2 − 2xy + 3x − 2y 2 + 3y.

Ответ: (x 2 + xy − 1)(x + y)(2y − 3) = 2x 3 y − 3x 3 + 4x 2 y 2 − 6x 2 y + 2xy 3 − 3xy 2 − 2xy + 3x − 2y 2 + 3y.

Источник