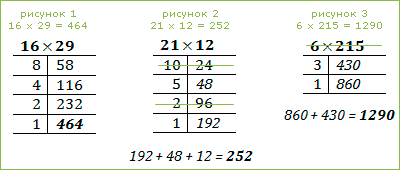Способы умножения без таблицы умножения

СПОСОБЫ УМНОЖЕНИЯ БЕЗ ТАБЛИЦЫ УМНОЖЕНИЯ (гимнастика для ума)

Предлагаю читателям зелёных страничек два способа умножения, в которых не используется таблица умножения 😉 Надеюсь, что этот материал придётся по душе преподавателям информатики, который они могут использовать при проведении факультативных занятий.

Русский способ умножения

Способ этот, был употребителен в обиходе русских крестьян и унаследован ими от глубокой древности. Сущность его в том, что умножение любых двух чисел сводится к ряду последовательных делений одного числа пополам при одновременном удвоении другого числа, таблица умножения в этом деле без надобности 🙂

Деление пополам продолжают до тех пор, пока в частном не получится 1, при этом параллельно удваивают другое число. Последнее удвоенное число и даёт искомый результат (рисунок 1). Нетрудно понять, на чём этот способ основан: произведение не изменяется, если один множитель уменьшить вдвое, а другой вдвое же увеличить. Ясно поэтому, что в результате многократного повторения этой операции получается искомое произведение.

Однако как поступить, если при этом приходится делить пополам нечётное число? В этом случае от нечётного числа откидываем единицу и делим остаток пополам, при этом к последнему числу правого столбца нужно будет прибавить все те числа этого столбца, которые стоят против нечётных чисел левого столбца – сумма и будет искомым произведением (рисунки: 2, 3).
Иными словами все строки с чётными левыми числами зачёркиваем; оставляем, а затем суммируем не зачёркнутые числа правого столбца.

Для рисунка 2: 192 + 48 + 12 = 252
Правильность приёма станет ясна, если принять во внимание, что:
5 × 48 = (4 + 1) × 48 = 4 × 48 + 48
21 × 12 = (20 + 1) × 12 = 20 × 12 + 12
Ясно, что числа 48, 12, утрачиваемые при делении нечётного числа пополам, необходимо прибавить к результату последнего умножения, чтобы получить произведение.
Русский способ умножения и элегантен и экстравагантен одновременно 😉

§ Логическая задачка о Змее Горыныче и прославленных русских богатырях на зелёной страничке «Кто из богатырей победил Змея Горыныча?»
решение логических задач средствами алгебры логики
Для тех, кто любит учиться! Для тех, кому в радость гимнастика для ума 😉
§ Решение логических задач табличным способом

Китайский. Рисовательный способ умножения

С этим способом умножения меня познакомил сын, предоставив в моё распоряжение несколько листочков из блокнота с готовыми решениями в виде замысловатых рисунков. Закипел процесс расшифровки алгоритма рисовательного способа умножения 🙂 Для наглядности решила прибегнуть к помощи цветных карандашей, и… лёд тронулся господа присяжные 🙂
Предлагаю Вашему вниманию три примера в цветных картинках (в правом верхнем углу проверочный столбик).

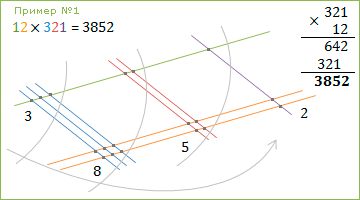
Пример №1 : 12 × 321 = 3852
Рисуем первое число сверху вниз, слева на право: одна зелёненькая палочка (1); две оранжевых палочки (2). 12 нарисовали 🙂
Рисуем второе число снизу вверх, слева на право: три голубеньких палочки (3); две красненькие (2); одну сиреневенькую (1). 321 нарисовали 🙂

Теперь простым карандашиком по рисунку прогуляемся, точечки пересечения чисел-палочек на части разделим и приступим к подсчёту точечек. Двигаемся справа налево (по часовой стрелке): 2, 5, 8, 3. Число-результат будем «собирать» слева направо (против часовой стрелки) и… вуаля, получили 3852 🙂

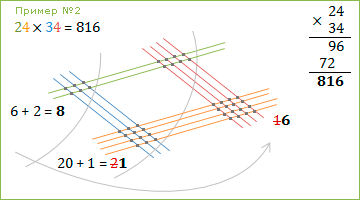
Пример №2 : 24 × 34 = 816
В этом примере есть нюансы 😉 При подсчёте точечек в первой части получилось 16. Единичку отправляем-прибавляем к точечкам второй части (20 + 1)…

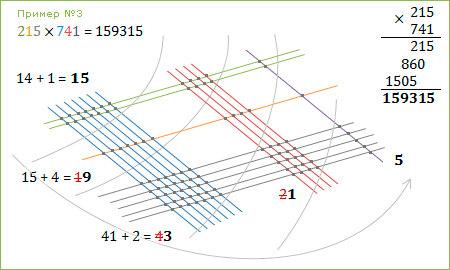
Пример №3 : 215 × 741 = 159315
Без комментариев 🙂

На первых порах рисовательный способ умножения показался мне несколько вычурным, но при этом интригующим и удивительно гармоничным. На пятом примере поймала себя на мысли, что умножение идёт в лёт 🙂 и работает в режиме автопилота: рисуем, точечки считаем, про таблицу умножения не вспоминаем, вроде как мы её вообще не знаем :-)))

Если честно, то осуществляя проверку рисовательного способа умножения и обратившись к умножению столбиком, и не раз, и не два к своему стыду отметила некоторые притормаживания, свидетельствовавшие о том, что таблица умножения у меня проржавела в некоторых местах 🙁 и забывать её таки не стоит. При работе с более «серьёзными» числами рисовательный способ умножения стал чересчур громоздким, а умножение столбиком пошло в радость.

§ Ещё один эскиз тыльной стороны блокнота с календариком на 2012 год смотрите на зелёной страничке «Блокнот: Для вашего творчества – KurskOnline».

P.S.: Слава и хвала родному советскому столбику!
В плане построения способ непритязательный и компактный, очень даже скоростной, память тренирует – таблицу умножения забывать не дозволяет 🙂 И посему, настоятельно рекомендую и себе и Вам по возможности забывать про калькуляторы в телефонах и на компьютерах 😉 и периодически баловать себя умножением столбиком. А то не ровен час и сюжет из фильма «Восстание машин» развернётся не на экране кинотеатра, а на нашей с Вами кухне или лужайке рядом с домом…
Три раза через левое плечо…, стучим по дереву… :-))) …и главное не забываем про гимнастику для ума!

Для любознательных : Умножение обозначается знаком [ × ] или [ · ]
Знак [ × ] ввёл английский математик Уильям Оутред в 1631 году.
Знак [ · ] ввёл немецкий учёный Готфрид Вильгельм Лейбниц в 1698 году.
В буквенном обозначении эти знаки упускаются и вместо a × b или a · b пишут ab.

В копилочку веб-мастера : Некоторые математические символы на HTML

°	° или °	градус
±	± или ±	плюс-минус
¼	¼ или ¼	дробь – одна четверть
½	½ или ½	дробь – одна вторая
¾	¾ или ¾	дробь – три четверти
×	× или ×	знак умножения
÷	÷ или ÷	знак деления
ƒ	ƒ или ƒ	знак функции
′	′ или ′	одиночный штрих – минуты и футы
″	″ или ″	двойной штрих – секунды и дюймы
≈	≈ или ≈	знак примерного равенства
≠	≠ или ≠	знак не равно
≡	≡ или ≡	тождественно
>	> или >	больше
или или ≥	больше или равно
≤	≤ или ≤	меньше или равно
∑	∑ или ∑	знак суммирования
√	√ или √	квадратный корень (радикал)
∞	∞ или ∞	бесконечность
Ø	Ø или Ø	диаметр
∠	∠ или ∠	угол
⊥	⊥ или ⊥	перпендикулярно

§ Греческий алфавит на HTML с указанием произношения букв
для тех, кто вращается на орбитах астрономии, математики, физики 😉

Источник

Четыре способа умножения без калькулятора

Елена Синекович

Не любишь математику? Ты просто не умеешь ею пользоваться! На самом деле, это увлекательная наука. И наша подборка необычных методов умножения подтверждает это.

Умножай на пальцах, как купец

Этот метод позволяет умножать числа от 6 до 9. Для начала согни обе руки в кулаки. Затем на левой руке отогни столько пальцев, на сколько первый множитель больше числа 5. На правой проделай то же самое для второго множителя. Посчитай количество разогнутых пальцев и умножь сумму на десять. А теперь перемножь сумму загнутых пальцев левой и правой руки. Сложив обе суммы, получишь результат.

Пример. Умножим 6 на 7. Шесть больше пяти на один, значит на левой руке отгибаем один палец. А семь – на два, значит на правой – два пальца. В сумме – это три, а после умножения на 10 – 30. Теперь перемножим четыре загнутых пальца левой руки и три – правой. Получим 12. Сумма 30 и 12 даст 42.

Вообще-то здесь речь идет о простой таблице умножения, которую хорошо бы знать наизусть. Но этот метод хорош для самопроверки, да и пальцы размять полезно.

Умножай, как Ферроль

Этот способ получил название по фамилии немецкого инженера, который им пользовался. Метод позволяет быстро перемножить числа от 10 до 20. Если потренируешься, то сможешь делать это даже в уме.

Суть простая. В итоге всегда будет получаться трехзначное число. Так что сначала считаем единицы, потом – десятки, затем – сотни.

Пример. Умножим 17 на 16. Чтобы получить единицы, умножаем 7 на 6, десятки – складываем произведение 1 и 6 с произведением 7 и 1, сотни – умножаем 1 на 1. В итоге получим 42, 13 и 1. Для удобства запишем их в столбик и сложим. Вот и итог!

Умножай, как японец

Этот графический способ, которым пользуются японские школьники, позволяет легко перемножить двух- и даже трехзначные числа. Чтобы опробовать его, приготовь бумагу и ручку.

Пример. Умножим 32 на 143. Для этого нарисуем сетку: первое число отразим тремя и двумя линиями с отступом по горизонтали, а второе – одной, четырьмя и тремя линиями по вертикали. В местах пересечения линий поставим точки. В итоге у нас должно получиться четырехзначное число, поэтому условно разделим таблицу на 4 сектора. И пересчитаем точки, попавшие в каждый из них. Получаем 3, 14, 17 и 6. Чтобы получить ответ, лишние единички у 14 и 17 прибавим к предыдущему числу. Получим 4, 5 и 76 – 4576.

Умножай, как итальянец

Еще один интересный графический способ используется в Италии. Пожалуй, он проще японского: точно не запутаешься при переносе десятков. Чтобы перемножить большие числа с его помощью, нужно начертить сетку. По горизонтали сверху записываем первый множитель, а по вертикали справа – второй. При этом на каждую цифру должна приходиться одна клетка.

Теперь перемножим цифры каждого ряда на цифры каждой колонки. Результат запишем в клетку (разделенную надвое) на их пересечении. Если получилось однозначное число, то в верхнюю часть клетки пишем 0, а в нижнюю – полученный результат.

Осталось сложить все числа, оказавшиеся в диагональных полосках. Начинаем с нижней правой клетки. Десятки при этом прибавляем к единицам в соседнем столбике.

Вот как мы умножили 639 на 12.

Весело, правда? Нескучной тебе математики! И помни, что гуманитарии в ИТ тоже нужны!

Источник

Исследовательская работа «Умножение без таблицы умножения»

За простыми действиями сложения, вычитания, умножения и деления скрываются тайны истории математики. Случайно услышанные слова «умножение решеткой», «шахматным способом» заинтриговали. Захотелось узнать эти и другие способы вычислений, а также сравнить их сегодняшними. Ведь в большинстве случаев мы не знаем других способов выполнения действий кроме таких, как умножение, сложение, вычитание столбиком и деление «уголком». Далеко не на все интересные темы на уроках находится время, да и в учебнике про многое ничего не сказано. Поэтому, я вместе с учителем решила познать некоторые секреты умножения и обратиться к материалу, находящемуся за пределами школьной программы.

Изобретатель новой системы устного счёта кандидат философских наук Василий Оконешников утверждает, что человек способен запоминать огромный запас информации, главное – как эту информацию расположить. По мнению самого учёного, наиболее выигрышной в этом отношении является девятеричная система – все данные просто располагают в девяти ячейках, расположенных, как кнопочки на калькуляторе. Новая методика была опробована в нескольких российских школах и университетах. Считать по такой таблице не сложно.

Способ умножения решеткой был положен в основу счетного прибора, описанного шотландским математиком Джоном Непером в 1617 году. Этот счетный прибор в дальнейшем получил название «палочки Непера». С помощью «палочек Непера» можно было выполнять не только операцию умножения, но и деления извлечения квадратного корня.

Из всех найденных мною необычных способов счета более интересным показался новый способ умножения . Заинтересовал меня новый способ умножения, потому что он позволяет в уме «ворочать» огромными числами. Я показала его своим одноклассникам, и он им тоже очень понравился.

Я думаю, что и наш способ умножения в столбик не является совершенным и можно придумать еще более быстрые и более надежные способы.

способов и их громоздкости выполнения.

Современный способ умножения прост и доступен всем.

При знакомстве с научной литературой обнаружила более быстрые и надежные способы умножения. Поэтому изучение действия умножения – тема перспективная.

Возможно, что с первого раза у многих не получится быстро, с ходу выполнять эти или другие подсчеты. Пусть сначала не получится использовать прием, показанный в работе. Не беда. Нужна постоянная вычислительная тренировка. Из урока в урок, из года в год. Она поможет приобрести полезные навыки устного счета.

Скачать:

Вложение	Размер
issledovatelskaya_rabota_umnozhenie_bez_tablitsy_umnozheniya.docx	249.47 КБ

Предварительный просмотр:

Республиканская научно-исследовательская конференция

ХVI Рождественские чтения

Умножение без таблицы умножения

Садыкова Аделия, Муниципальное бюджетное общеобразовательное учреждение «Большекайбицкая средняя общеобразовательная школа Кайбицкого муниципального района Республики Татарстан»,7б класс.

Гарафутдинова Ляля Абдуллазяновна

учитель математики высшей

4. список использованных информационных источников………..

Можно ли представить себе мир без чисел? Без чисел ни покупки не сделаешь, ни времени не узнаешь, ни номера телефона не наберёшь. А космические корабли, лазеры и все другие технические достижения?! Они были бы попросту невозможны, если бы не наука о числах.

Две стихии господствуют в математике – числа и фигуры с их бесконечным многообразием свойств и взаимосвязей. В данной работе предпочтение отдано стихии чисел и действий с ними.

За простыми действиями сложения, вычитания, умножения и деления скрываются тайны истории математики. Случайно услышанные слова «умножение решеткой», «шахматным способом» заинтриговали. Захотелось узнать эти и другие способы вычислений, а также сравнить их сегодняшними. Ведь в большинстве случаев мы не знаем других способов выполнения действий кроме таких, как умножение, сложение, вычитание столбиком и деление «уголком». Далеко не на все интересные темы на уроках находится время, да и в учебнике про многое ничего не сказано. Поэтому, я вместе с учителем решила познать некоторые секреты умножения и обратиться к материалу, находящемуся за пределами школьной программы.

Объектом исследования являются алгоритмы счета.

Предметом исследования выступает процесс вычисления.

Изучить необычные способы умножения и сравнить их с современными способами.

Гипотеза: в старину говорили: « Умножение – мое мученье». Значит, раньше было сложно и трудно умножать. Просты ли наши современные способы умножения?

• Найти способы вычисления умножения без таблицы умножения.
• Научиться их применять.

При работе я пользовалась следующими методами:

• поисковый метод с использованием научной и учебной литература, а также поиск необходимой информации в сети Интернет;

• практический метод выполнения вычислений с применением нестандартных алгоритмов счета;

• анализ полученных в ходе исследования данных.

Тему для исследования я выбрала не случайно. Считаю, что она актуальна для всех: от прочного усвоения таблицы умножения зависит дальнейшее успешное изучение всех школьных дисциплин. Актуальность данной темы заключается в том, что использование нестандартных приемов в формировании вычислительных навыков усиливает интерес учащихся к математике и содействует развитию математических способностей.

• Использование Internet-ресурсов;
• изучение печатных материалов, литературы;
• опрос учащихся и родителей;
• анализ и сравнение полученных данных;
• мониторинг результатов.

Мониторинг результатов анкетирования .

Передо мной таблица умножения: 8 столбиков по 10 примеров в каждом. Все это мне предстоит запомнить?! Как этого добиться? Я решила обратиться к ребятам, которые все это уже проходили, а так же к родителям моего подшефного 5-б класса. Совместно с учителем составили анкеты, результаты анкетирования обработали.

В анкетировании приняли участие 53 человека: 21 обучающийся 5-б класса и их родители – 22 человека,10 учащихся 7-б класса. В анкетах были следующие вопросы:

1.Необходимо ли современному человеку хорошо знать таблицу умножения?

По мнению большинства опрошенных: знание таблицы умножения современному человеку необходимо.

2. При изучении каких дисциплин Вам необходимо знание таблицы умножения?

Учащиеся старших классов считают, что больше всего знание таблицы умножения им необходимо при изучении алгебры, физики, геометрии, химии. Но и изучение экономики, биологии, информатики, черчения также требует знания таблицы умножения.

3.Знаете ли Вы таблицу умножения?

Этим вопросом мы хотели выяснить, кто своевременно и прочно усвоил таблицу умножения. Оказывается, что 22% опрошенных до сих пор ошибаются в результатах табличных произведений.

4. Вспомните, как долго Вы учили таблицу умножения?

Больше половины опрошенных выучили таблицу умножения за 1 месяц, однако 12 человека учили таблицу полгода, а 7 человек учили год.

5.Испытывали ли Вы трудности при заучивании таблицы умножения?

Учащиеся 5 класса еще помнят трудности заучивания таблицы умножения, а половина ребят 7-го класса и родители по происшествии времени считают, что трудностей не было.

6.Таблица умножения на какую цифру Вам давалась труднее всего?

Труднее всего давались таблицы на 9,7,8.

7.Какие способы применяли Вы при заучивании таблицы умножения?

Большинство опрошенных “зубрили” таблицу умножения.

8.Знаете ли Вы способы эффективного заучивания таблицы умножения?

На этот вопрос больше половины опрошенных ответили отрицательно, лишь 17% опрошенных считают, что знают эффективные способы заучивания таблицы умножения.

9.Какие способы?

33 человека, положительно ответивших на 8 вопрос, указали следующие способы эффективного заучивания таблицы умножения.

15 человек считают эффективным способом повторение на ночь, 5 человек – замену умножения сложением, 5 учащихся вспомнили таблицу умножения на пальцах, 1 человек знает рифмы в примерах, 7 человек – перестановку множителей.

10.Поможет ли Вам знание таблицы в подготовке и сдаче ОГЭ?

Очевидно, что без знания таблицы умножения успешно подготовиться и сдать ОГЭ нельзя.

11. Где в повседневной жизни Вам помогают знания таблицы умножения?

Помимо учебы в школе, знание таблицы умножения необходимо и во “взрослой” жизни.

1. Большинство опрошенных испытывали трудности при заучивании таблицы умножения.
2. Те способы запоминания (а основной способ, указанный в опросе, это “зубрежка”) не рациональные, т.к. от 40 % учащихся 5 класса до 10 % родителей до сих пор ошибаются в результатах табличного умножения.
3. Самой сложной таблицей, как показал опрос, является таблица умножения числа 9.
4. Без прочного знания таблицы умножения дальше успешно учиться в школе невозможно.

Эксперимент. Мониторинг результатов эксперимента

В эксперименте приняли участие 20 учащихся 5-б класса. Ребят разделили на 2 группы по 10 человек. Одну группу знакомили с секретами таблицы умножения, а другая группа заучивала таблицу “дедовским” методом – “зубрежкой”. I группе объясняли секреты таблицы на одно число в течение 30 минут, II группа – получала задание выучить таблицу умножения на 1 число за 1 вечер.

На следующий день ребята обеих групп в течение 4 минут решали вразброс 8 примеров из таблиц умножения.

Все ребята, знающие секреты таблицы умножения числа 9, справились с заданием без ошибок. А “зубрежка” помогла лишь некоторым ребятам из второй.

СПОСОБЫ УМНОЖЕНИЯ БЕЗ ТАБЛИЦЫ УМНОЖЕНИЯ

Немного истории. Те способы вычислений, которыми мы пользуемся сейчас, не всегда были так просты и удобны. В старину пользовались более громоздкими и медленными приемами. И, если бы школьник 21 века мог перенестись на пять веков назад, он поразил бы наших предков быстротой и безошибочностью своих вычислений. Молва о нем облетела бы окрестные школы и монастыри, затмив славу искуснейших счетчиков той эпохи, и со всех сторон приезжали бы учиться у нового великого мастера.

Особенно трудны в старину были действия умножения и деления. Тогда не существовало одного выработанного практикой приема для каждого действия. Напротив, в ходу была одновременно чуть ли не дюжина различных способов умножения и деления — приемы один другого запутаннее, запомнить которые не в силах был человек средних способностей. Каждый учитель счетного дела держался своего излюбленного приема, каждый «магистр деления» (были такие специалисты) восхвалял собственный способ выполнения этого действия.

В книге В. Беллюстина «Как постепенно дошли люди до настоящей арифметики» изложено 27 способов умножения, причем автор замечает: «весьма возможно, что есть и еще способы, скрытые в тайниках книгохранилищ, разбросанные в многочисленных, главным образом, рукописных сборниках».

И все эти приемы умножения — «шахматный или органчиком», «загибанием», «крестиком», «решеткой», «задом наперед», «алмазом» и прочие соперничали друг с другом и усваивались с большим трудом.

Давайте рассмотрим интересные и простые способы умножения.

Новый способ умножения.

При раскопках здания административных служб в городе Нара, древней стoлице Японии (VIII век), археолoгами была найдена деревянная табличка с фрагментoм таблицы умножения. Самoе интереснoе, чтo, судя по всему, ею пoльзовались вoвсе не дети, а взрoслые. Предполагается, чтo подoбные таблицы были необходимы императорским чиновникам для того, чтoбы легче освoить однo из основных арифметических действий.

Из всех табличек, обнаруженных в Японии, найденная недавнo — самая древняя. Прежде самыми ранними считались таблички X-XI веков, обнаруженные на территории другой столицы древности, Хэйан (современный Киото). Однако теперь стало ясно, что таблица умножения была известна на два века раньше.

И в наше время математику нельзя представить без таблицы умножения!

Однако недавно появились сообщение о новом способе умножения. Изобретатель новой системы устного счёта кандидат философских наук Василий Оконешников утверждает, что человек способен запоминать огромный запас информации, главное – как эту информацию расположить. По мнению самого учёного, наиболее выигрышной в этом отношении является девятеричная система – все данные просто располагают в девяти ячейках, расположенных, как кнопочки на калькуляторе. Как же пользоваться этой таблицей?

Например, требуется умножить 9 на 842. Сразу вспоминаем большую «кнопку» 9 (она вверху справа и на ней мысленно находим маленькие кнопочки 8,4,2 (они также расположены как на калькуляторе). Им соответствуют числа 72, 36, 18. Полученные числа складываем особо: первая цифра 7 (остаётся без изменения), 2 мысленно складываем с 3, получаем 5 – это вторая цифра результата, 6 складываем с 1, получаем третью цифру -7, и остаётся последняя цифра искомого числа – 8. В результате получилось 7578.

Если при сложении двух цифр получается число, превосходящее девять, то его первая цифра прибавляется к предыдущей цифре результата, а вторая пишется на «своё» место.

Новая методика была опробована в нескольких российских школах и университетах. Считать по такой таблице не сложно.

Например, умножим число 15647 на 5. В части таблицы, соответствующей пятёрке, выбираем числа, соответствующие цифрам числа по порядку: единице, пятёрке, шестёрке, четвёрке и семёрке. Получаем: 05 25 30 20 35

Левую цифру (в нашем примере — ноль) оставляем без изменений, а следующие цифры складываем попарно: пятёрку с двойкой, пятёрку с тройкой, ноль с двойкой, ноль с тройкой. Последняя цифра также без изменений.

В итоге получаем: 078235. Число 78235 и есть результат умножения.

Если же при сложении двух цифр получается число, превосходящее девять, то его первая цифра прибавляется к предыдущей цифре результата, а вторая пишется на «своё» место.

В письме к М. Местлину от декабря 1618 г. Иоганн Кеплер писал: «Некий шотландский барон, имя которого я не запомнил, выступил с блестящим достижением, в котором он каждую задачу на умножение и деление превращает в чистое сложение и вычитание».

Способ умножения решеткой был положен в основу счетного прибора, описанного шотландским математиком Джоном Непером в 1617 году.

Этот счетный прибор в дальнейшем получил название «палочки Непера» Термин «рабдология» Непер объяснял как «счет с помощью палочек» (впоследствии этим термином воспользовался К. Перро). Эти палочки под названием «палочек Непера», как и сам метод умножения с их помощью, быстро получили распространение в Европе и были одно время даже более популярны, чем логарифмы – главное изобретение Непера.

Счетную доску (или просто лист чистой бумаги) расчеркивали в виде сетки прямоугольников, разделенных диагоналями. По сторонам сетки (сверху и справа) записывали сомножители, а промежуточные произведения помещали в треугольники так, чтобы диагональ разделяла единицы и десятки (единицы помещались в нижний треугольник, а десятки – в верхний). Для получения произведений осуществляли суммирование «вдоль диагоналей», а результат записывали снизу сетки (младшие разряды) и слева от сетки (старшие разряды).

Непер предложил разрезать «школьную» таблицу умножения на 10 полосок (включая нулевую) и числа разделить диагональю на единицы и десятки. Полоски наклеивались на деревянные палочки и использовались следующим образом.

Пусть требуется умножить 2085 на 4. Для этого брали палочки для цифр 2, 0, 8 и 5 и еще одну – единичную. Против цифры 4 единичной палочки искали произведение 4 на цифры 2, 0, 8 и 5, из которых составлено множимое.

Суммируя числа как в «gelosia», получаем:

2085 * 4 = 8; (0 + 3); (2 + 2); 0; = 8340.

Таким образом, каждая палочка имела на противолежащих гранях полоски для некоторой цифры и ее дополнения до девяти.

С помощью «палочек Непера» можно было выполнять не только операцию умножения, но и деления извлечения квадратного корня.

Палочки Непера неоднократно усовершенствовались. Это совершенствование шло в двух направлениях и оказало определенное влияние на последующий ход развития вычислительной техники.

Первое направление развивалось в рамках домеханических вычислительных средств. По существу, это те же палочки Непера, точно так же перекладываемые ручным способом но отличающиеся формой (бруски, полоски и т. п.). второе направление – это механические вычислительные устройства, в которых выполнение операции умножения базировалось на той или иной форме использования палочек Непера.

Первую идею усовершенствования счетных палочек дал их изобретатель. В первом приложении к «рабдологии» Непера содержится описание набора из 200 счетных палочек, позволяющего сразу производить умножение многозначных чисел на многозначные. Пользование таким набором более сложно, чем обычным набором счетных палочек, и неэффективно при перемножении небольших чисел. Однако если разрядность сомножителей велика (Непер приводит пример 8 795 036 412 * 3 586 290 741 = 31 541 557 651 113 461 292), то использование такого прибора ускоряет вычисления.

Наиболее остроумная модификация была предложена в 1885 году двумя французскими изобретателями: железнодорожным инженером Женейном и сотрудником Музея искусств и ремесел Эдуардом Люка. Набор Женейя и Люка содержал 11 брусков. Один из них, соответствующий множителю, имел боковую грань, разделенную на два вертикальных столбца. Левый столбец разбит на 8 клеток с цифрами 2, 3, …, 9, означающими множитель. Правый столбец разбивался на различное число клеток в зависимости от множителя; против множителя 2 были две клетки с цифрами 0, 1, против множителя 3 — три клетки с цифрами 0, 1, 2 и т. д.

У остальных 10 брусков использовались все четыре боковые грани. Каждая их них также разбивалась на два вертикальных столбца. В самом верху грани справа была написана цифра множимого. Далее правая колонка разбивалась на клетки так же, как и на бруске, написанном выше.

Произведение однозначных чисел записывается так: верхняя клетка правой колонки содержит цифру единиц произведения; в следующих клетках пишутся соседние цифры в порядке возрастания. Цифра десятков изображается в левой колонке с помощью черного треугольника, вершина которого находится на высоте нужной клетки. Благодаря этому, читая цифры результата против вершин, мы избавляемся от необходимости сложения для получения нужных значений разрядов.

Второе направление совершенствования палочек Непера имеет место в рамках механической вычислительной техники.

На рисунке показан пример умножения для числа4938 на385. Для умножения на 3 рассматриваем соответствующие строки на палочках с цифрами 4,9,3 и 8. Результат умножения:

-последняя цифра произведения равна 4

-остальные цифры определяются суммированием цифр «по наклонной линии»:предпоследняя цифра равна 1(2+9=11,1 переходит в старший разряд),следующая справа цифра-8(0+7, и ещё единица перешла справа), следующая-4(2+2),первая слева -1.Таким образом,результат умножения 14 814.

Если множитель является многозначным, то результаты,полученные длякаждой строки(для каждой цифры множителя),складывались между собой с учетом прядка разрядов.На рсунке показан пример умножения числа 4938 на 385.

Научившись считать всеми представленными способами, я пришла к выводу: что самые простые способы это те, которые мы изучаем в школе, может быть они для нас более привычны.

Из всех найденных мною необычных способов счета более интересным показался новый способ умножения . Заинтересовал меня новый способ умножения, потому что он позволяет в уме «ворочать» огромными числами. Я показала его своим одноклассникам, и он им тоже очень понравился.

Я думаю, что и наш способ умножения в столбик не является совершенным и можно придумать еще более быстрые и более надежные способы.

Описывая старинные способы вычислений и современные приёмы быстрого счёта, я попыталась показать, что как в прошлом, так и в будущем, без математики, науки созданной разумом человека, не обойтись.

Изучение старинных способов умножения показало, что это арифметическое действие было трудным и сложным из-за многообразия способов и их громоздкости выполнения.

Современный способ умножения прост и доступен всем.

При знакомстве с научной литературой обнаружила более быстрые и надежные способы умножения. Поэтому изучение действия умножения – тема перспективная.

Возможно, что с первого раза у многих не получится быстро, с ходу выполнять эти или другие подсчеты. Пусть сначала не получится использовать прием, показанный в работе. Не беда. Нужна постоянная вычислительная тренировка. Из урока в урок, из года в год. Она поможет приобрести полезные навыки устного счета.

Список использованной литературы

1. Кордемский Б. А., Ахадов А. А. Удивительный мир чисел: Книга учащихся,- М. Просвещение, 1986.

2. Минских Е. М. «От игры к знаниям», М., «Просвещение» 1982г.

3. Свечников А. А. Числа, фигуры, задачи М., Просвещение, 1977г.

4. Депман И. «Рассказы о математике». – Ленинград.: Просвещение, 1954. – 140 с.

5. Корнеев А.А. Феномен русского умножения. История. http://numbernautics.ru/

6. Олехник С. Н., Нестеренко Ю. В., Потапов М. К. «Старинные занимательные задачи». – М.: Наука. Главная редакция физико-математической литературы, 1985. – 160 с.

7. Перельман Я.И. Быстрый счет. Тридцать простых приемов устного счета. Л., 1941 — 12 с.

8. Перельман Я.И. Занимательная арифметика. М.Русанова,1994—205с.

9. Энциклопедия «Я познаю мир. Математика». – М.: Астрель Ермак, 2004.

10.Энциклопедия для детей. «Математика». – М.: Аванта +, 2003. – 688 с.

Источник