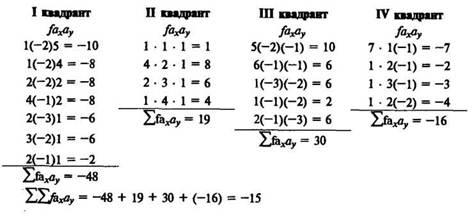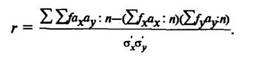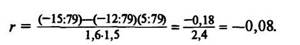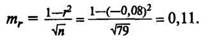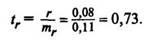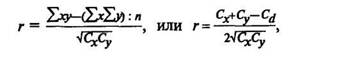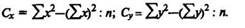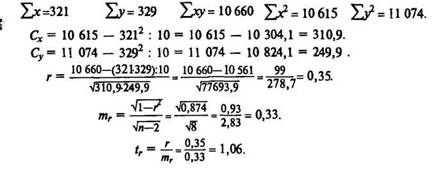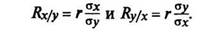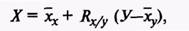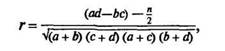Способы связи между признаками

ИЗУЧЕНИЕ СВЯЗИ МЕЖДУ ПРИЗНАКАМИ

Признаки и свойства животных находятся в определенной взаимосвязи. Например, существует связь между устойчивостью и восприимчивостью матерей и их дочерей к маститу, лейкозу и т. д., между фагоцитарной активностью и резистентностыо, уровнем кормления и молочной продуктивностью, длиной туловища и живой массой. Особенность корреляции (связи) между признаками живых организмов состоит в том, что каждому значению одного признака соответствует не одно, а несколько значений другого. Так, животные одинаковой высоты могут быть разными по массе, но в среднем масса низких животных меньше более высоких.

Различают положительную и отрицательную корреляции. При положительной корреляции с увеличением одного признака увеличивается и другой. Например, с увеличением массы коров-первотелок возрастает и удой; чем выше процент жира в молоке, тем выше и процент белка в нем. При отрицательной корреляции с увеличением одного признака второй уменьшается. Например, с увеличением удоя у коров снижается жирность молока; чем больше длина туловища у свиней, тем меньше толщина сала; куры с высокой яйценоскостью имеют более мелкие яйца и т. д.

Для оценки силы и направления взаимосвязи между признаками вычисляют коэффициент корреляции (г). Он колеблется от О до ±1. При положительной корреляции его величина может изменяться от 0 до +1, а при отрицательной — от 0 до — 1. Когда коэффициент корреляции равен нулю, то изменение одного признака происходит независимо от другого. Если коэффициент корреляции ниже 0,5, то связь считается слабой; при величине г, равной 0,5—0,6, — средней; если коэффициент 0,7 и выше, — связь высокая.

Вычисление коэффициента корреляции (г) для большой выборки (л > 30). Вычислим величину корреляции между количеством эритроцитов (млн в 1 мм 3 ) и лейкоцитов (тыс. в 1 мм 3 ) у 79 коров черно-пестрой породы. Для этого определяют классы для вариационного ряда по количеству эритроцитов и отдельно по количеству лейкоцитов. Потом составляют корреляционную решетку (табл. 19) и записывают в ней вверху по горизонтали значения

классов по количеству эритроцитов (х) от минимального к максимальному, а по вертикали располагают классы по количеству лейкоцитов (у) от больших к меньшим. Заносят данные о 79 животных в клетки корреляционной решетки с учетом одновременно значений двух признаков. Так, если в крови коровы содержится 6,6 млн эритроцитов и 7,4 тыс. лейкоцитов, то ее отмечают одной точкой в клетке на пересечении класса 6,5—6,9 по количеству эритроцитов и класса 7,0—7,9 по количеству лейкоцитов. Подсчитывают частоту вариант fx nf_y. Выделяют жирными линиями классы условной средней Ах (6,5—6,9) и А_у (7—7,9).

Коэффициент корреляции вычисляют по формуле

Сигмы берутся без классного промежутка:

В решетке образуется четыре квадранта. Определяют ряд условных отклонений а_х и а_у. Находят ряды произведений fxa_x_> fyOy, fxOx,fyOy и их суммы. Вычисляют произведение fa^ay по каждому из четырех квадрантов [для этого частоту (/) каждой клеткилгмножают на соответствующее значение а_х и а_у\.

Ошибка коэффициента корреляции. Так как коэффициент корреляции вычислен не по генеральной, а по выборочной совокупности, он имеет ошибку выборочности:

Достоверность коэффициента корреляции. Когда известна ошибка, можно определить степень достоверности г. При этом исходят из нулевой гипотезы, т. е. предполагают, что в генеральной совокупности связь между изучаемыми признаками отсутствует. Только при значении t_r, равном табличному значению или больше его (при вероятности 0,95; 0,99 или 0,999), нулевая гипотеза отвергается и значение г будет достоверным. В примере

С учетом числа степеней свободы v = п — 2 = 79 — 2 = 77, находим значения t_st (см. табл. 13). Они равны: = 1,96, /0,99 = 2,58 и /Ь,999 = 3,29. Так как наше значение t_r = 0,73 меньше tgt= 1,96, то нулевая гипотеза не отвергнута и мы не можем сказать, что у исследованных коров существует слабая отрицательная корреляция между количеством эритроцитов и лейкоцитов.

Вычисление коэффициента корреляции для малых выборок (л

20. Определение г для малых выборок

Номер	Нейтрофилы, %	*	у 2
коровы	матери (х)	дочери (у)	ху	X
36 40
29 22
38 32
20 32
39 34
28 33
30 24
38 40
32 35
31 36

Находим значение fa (см. табл. 13), которое с учетом числа степеней свободы v = n — 2=10 — 2 = 8 равно /о,95 = 2,31. В связи с тем что фактически полученный t_r = 1,06 меньше значения fa = 2,31, коэффициент корреляции недостоверен. Для того чтобы коэффициент корреляции г = 0,35 был достоверен (при р = 0,95), нужно было взять не менее 32 пар значений признака. Имеются специальные таблицы (Г. Лакин. Биометрия. М., 1990, с. 344), по которым можно узнать количество пар значений признака, достаточное для достоверности выборочного коэффициента корреляции.

В исследованиях, проведенных на больших выборках, установлена положительная связь между относительным числом активных нейтрофилов у матерей и дочерей. Если удвоить коэффициент корреляции, вычисленный по какому-нибудь признаку между матерями и дочерями, то получим коэффициент наследуемости (й 2 = 2г_м/_д), который указывает на долю генетической изменчивости в общей фенотипической изменчивости признака.

Коэффициент регрессии. Коэффициент корреляции указывает-только на степень связи между признаками. Иногда необходимо знать характер изменения одного признака в зависимости от изменения другого. Для этих целей используется регрессионный анализ. Коэффициент регрессии показывает, насколько изменяется один признак при изменении другого на единицу. Он вычисляется по формуле

Регрессия является двухсторонней, т. е. можно определить изменение х по изменению у и изменение у по изменению х. В формуле среднее квадратическое отклонение берется с учетом классного промежутка. Например, коэффициент корреляции между удоем за первую (х) и вторую (у) лактации равен 0,6, а_х = 700 кг, а^ = 900кг. Отсюда R_y/_X = 0,6(900:700) = 0,77 кг. ^го значит, что с увеличением удоя по первой лактации на 1 кг удой по второй лактации увеличивается на 0,77 кг. Вычисляем Rx/y = 0,6(700:900) = 0,47 кг. В этом случае с увеличением удоя по второй лактации на 1 кг удой по первой лактации увеличивается на 0,47 кг. В одном хозяйстве удой первотелок равен х_х = 4240 кг, а у коров за вторую лактацию х_у = 4870 кг. Если мы отберем первотелок с удоем, например, на 100 кг выше среднего — 4340 кг, то у этих коров по второй лактации при R_y/_X = 0,77 удой составит 4870 + 0,77-100 = 4947 кг. Поэтому, зная коэффициент регрессии, можно определить величину одного признака при заданной величине другого признака по уравнению прямолинейной регрессии:

где X— искомая величина признака х; У— заданная величина признака у; хх и ху — соответствующие средние арифметические признаков.

По этому уравнению можно, например, предсказать, какой удой будет у коров по второй лактации, если по первой он составлял 5000 кг: У= х_у+Ry/xx) = 4870 + 0,77 (5000 — — 4340) = 4870 + 0,77 • 660 = 5378 кг. Следовательно, если у группы коров удой по первой лактации был 5000 кг, то по второй лактации он составит 5378 кг.

Коэффициент корреляции между альтернативными признаками (/д). Для установления связи между альтернативными признаками строят четырехклеточную корреляционную решетку (табл. 21). Коэффициент корреляции вычисляют по формуле

где а, Ь, с, //—частоты, распределившиеся в четырех клетках корреляционной решетки.

21. Корреляция частоты заболеваемости лейкозом матерей и дочерей

Дочери (у)

Матери

(х)

Всего

больные

здоровые

Больные Здоровые Всего

а = 46 с= 114 а + с = 160

6 = 70 rf = 391 Ь + d=46l

а + Ь= 116 с + l ~~fel~~ 4 ~~. 7~~ = 0,039.
i^- V621

Достоверность коэффициента корреляции t_r= ~~°^₉~~ = 3,77.

Так как t = 3,77 больше табличного значения у = 3,29 (см. табл. 13), коэффициент корреляции высокодостоверен (р > 0,999).

Таким образом, можно сделать вывод, что между частотой заболеваемости лейкозом матерей-коров и их дочерей существует невысокая положительная связь, т. е. у больных матерей дочери чаще заболевают лейкозом, чем у здоровых.

Коэффициент регрессии вычисляют по формулам

Источник

Основные формы корреляционной связи между признаками

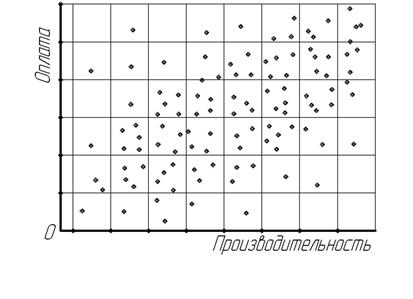
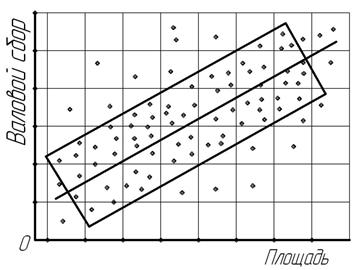
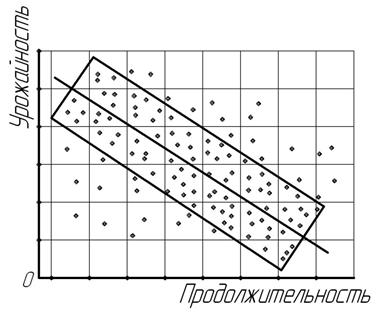
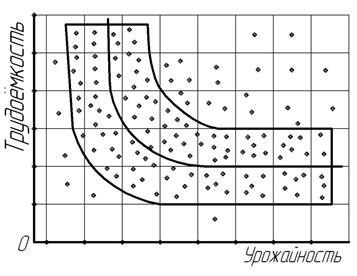
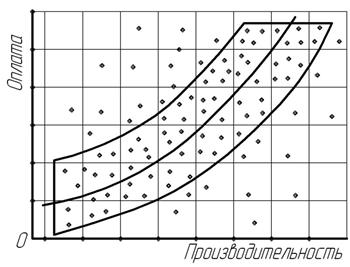
Выявлению формы связи между признаками предшествует определение причинной зависимости между ними. Это наиболее важный и ответственный момент для правильного использования корреляционного метода. По каждому изучаемому явлению предварительно необходимо установить, какие логические причины лежат в основе связи между признаками-факторами и признаками-результатами.

Выявление формы связи между признаками сводится к выбору математического уравнения, которое могло бы наиболее полно и точно отразить характер взаимосвязи между изучаемыми признаками. Любая форма корреляционной связи между признаками, выступая как внешнее проявление причинно-следственной зависимости в экономических явлениях, естественно, отражает и общий характер внутреннего содержания этой взаимосвязи. Поэтому установление формы связи между признаками –– важный этап изучения корреляционной зависимости.

Влияние одного или нескольких факторов на результативный признак приводит к формированию различных по содержанию и форме корреляционных зависимостей. В экономических явлениях могут иметь место самые разнообразные формы корреляционной связи, так как с возрастанием факторного признака возможно не только более-менее равномерное увеличение или убывание признака-результата, но и неравномерное, непропорциональное его изменение. В связи с этим различают близкую к прямолинейной и криволинейную формы простой (парной) корреляционной связи.

Для ориентировочного выявления эмпирической формы корреляционной зависимости могут применяться различные статистические приемы, среди которых наиболее распространенный, наглядный и доступный – графический способ. На координатной диаграмме, где по оси абсцисс откладывают значения признака-фактора, а по оси ординат – значения признака-результата, изображают поле корреляции (рис.11.1), которое представляет собой совокупность точек, размещенных на плоскости в системе координат.

Рис. 11.1. Поле корреляции, характеризующее взаимосвязь годовой производительности и оплаты труда в организациях АПК

Эмпирическую форму корреляционной связи обычно выявляют по направленности основной массы точек, сосредоточенных в поле корреляции. Наглядным естественным примером корреляционного поля может служить Млечный путь, где наблюдается повышенная концентрация звезд. Вытянутость этого пути с востока на запад указывает на форму, близкую к прямолинейной.

Прямолинейная простая (парная) корреляционная зависимость характеризуется возрастанием или убыванием на более-менее определенную величину результативных признаков при непрерывном возрастании факторных признаков. При прямой, близкой к прямолинейной, корреляционной связи увеличение фактора сопровождается повышением результата, при обратной – рост факторного признака вызывает снижение результативного. Графическое изображение прямой и обратной корреляционной связи показано на рис.11.2 и 11.3.

Рис. 11.2. Взаимосвязь валового сбора и посевной площади картофеля в крестьянских (фермерских) хозяйствах (корреляционная прямая зависимость)

Рис. 11.3. Взаимосвязь урожайности и продолжительности уборки зерновых культур в сельскохозяйственных организациях (корреляционная обратная зависимость)

Основная масса точек на этих рисунках ограничена прямоугольниками и проведены эмпирические прямые линии регрессии, предназначенные для лучшего понимания не только формы, но и содержания прямолинейной (прямой и обратной) корреляционной зависимости. На рис.11.2 наглядно видно, что рост фактора вызывает почти прямолинейное повышение результата, а на рис.11.3 –– увеличение факторного признака сопровождается близким к прямолинейному снижением результативного признака.

Криволинейные парные корреляционные связи в экономических явлениях могут выражаться в разнообразные формах: гиперболической, параболической, экспоненциальной, синусоидальной и т.д. Для наглядного представления о некоторых формах корреляционной зависимости приведено их графическое изображение (рис. 11.4 – 11.6).

Рис. 11.4. Взаимосвязь трудоёмкости и урожайности сахарной свеклы в сельскохозяйственных организациях (корреляционная гиперболическая зависимость)

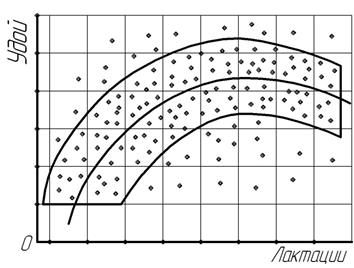
Рис. 11.5. Взаимосвязь годового удоя и числа лактаций коров в сельскохозяйственных организациях (корреляционная параболическая зависимость)

Рис. 11.6. Взаимосвязь коммерческих цен и темпов роста инфляции

(корреляционная экспоненциальная зависимость)

На рис. 11.4 видно, это рост признака-фактора на начальной стадии приводит к резкому падению, а в дальнейшем – замедленному снижению признака-результата. Это характерная особенность гиперболической формы корреляционной связи. В отличие от предыдущей формы зависимости, на рис. 11.5 показана более сложная, параболическая корреляционная связь, где изменение результативного признака можно условно разделить на три стадии: на начальной наблюдается довольно быстрое повышение, далее признак-результат достигает апогея и, наконец, этот же признак претерпевает существенный спад.

Выявление и установление формы корреляционной зависимости –– одна из важнейших задач корреляционно-регрессионного метода. Во-первых, значение конкретной формы связи способствует поиску наиболее точного способа измерения тесноты связи между факторным и результативным признаками; во-вторых, это облегчает выбор корреляционного уравнения регрессии, которое в наибольшей мере соответствует содержанию и характеру корреляционной зависимости.

Множественная корреляция, т.е. статистическая зависимость результативного признака от нескольких признаков-факторов, по форме не отличается от парной корреляционной связи. Вместе с тем выявление формы множественной связи в значительной мере затруднено. Поэтому решению множественного корреляционного комплекса обычно предшествует разработка соответствующих вопросов по однофакторным корреляционным моделям.

Источник