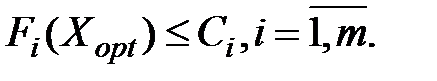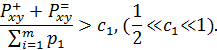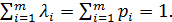Сужение множества Парето
Я на практических занятиях Вам приводил пример «Выбор места работы». Мы нашли множество Парето оптимальных решений.
Было определено, что оптимизация по Парето использует отношение Парето-доминирования, которое отдаёт предпочтение одному объекту перед другим только» том случае, когда первый объект по всем критериям не хуже второго и хотя бы но одному из них лучше. При истинности этого условия первый объект считается доминирующим, а второй — доминируемым. Два объекта, для которых предпочтение хотя бы, по одному критерию расходится, считаются несравнимыми.
Очевидно, что выделение множества Парето часто не является удовлетворительным решением. Это связано с тем, что при достаточно большом исходном множестве вариантов множество Парето оказывается недопустимо большим для того, чтобы ЛПР было бы в состоянии осуществить выбор самостоятельно. Таким образом, выделение множества Парето можно рассматривать лишь как предварительный этап оптимизации, и налицо проблема дальнейшего сокращения этого множества.
Для выбора одной оптимальной стратегии из множества эффективных решений в каждой конкретной многокритериальной задаче необходимо использовать дополнительную информацию.
Общая методика исследования задач принятия решения на основе математического моделирования для задач МКО должна быть реализована в рамках одного из следующих подходов.
Первый подход. Для заданной многокритериальной задачи оптимизации находится множество её Парето-оптимальных решений, а выбор конкретного оптимального варианта из множества Парето-оптимальных предоставляется ЛПР.
Второй подход. Производится сужение множества Парето-оптимальных исходов (в идеале – до одного элемента) с помощью некоторых формализованных процедур, что облегчает окончательный исход для ЛПР.
Рассмотрим некоторые простейшие способы сужения Парето-оптимального множества, акцентируя при этом внимание на необходимость дополнительной информации.
Указание верхних/нижних границ критериев. Дополнительная информация об оптимальном исходе Xopt ÎD в этом случае имеет вид
Число Ci рассматривается здесь как верхняя граница по i – му критерию. Соответственно для установления нижних границ используется знак «больше или равно».
Наложим, например, следующие ограничения на оптимальное решение:
· зарплата — не менее 500 рублей;
Отбрасывается 5 вариант
· длительность отпуска — не менее 30 дней;
Остаются все варианты
· время поездки — не более 40 минут.
Отбрасывается 4 и 7 варианты
Варианты, удовлетворяющие этим дополнительным ограничения: из них оптимальными по Парето являются варианты 3 и 6. Остаётся сделать окончательный выбор между вариантами 3 и 6.
Основной недостаток метода состоит в том, что оптимальное решение становится здесь субъективным, так как зависит, во — первых, от величин назначаемых верхних/нижних границ критериев и, во-вторых, от окончательного выбора, совершаемого принимающим решение.
Субоптимизация. производят следующим образом: выделяют один из критериев, а по всем остальным критериям назначают нижние границы. Оптимальным при этом считается исход, максимизирующий выделенный критерий на множестве исходов, оценки которых по остальным критериям не ниже назначенных.
Пусть в качестве главного критерия выступает критерий зарплата; ограничения
· длительность отпуска — не менее 30 дней;
· время поездки — не более 40 минут.
Отбросим варианты, которые не удовлетворяют данным ограничениям: . Из них максимальную зарплату имеет вариант 3. Этот вариант и будет оптимальным.
Лексикографическая оптимизация Основана на упорядочении критериев по их относительной важности. Процедуру нахождения оптимального решения проводят следующим образом: На первом шаге отбирают исходы, которые имеют максимальную оценку по важнейшему критерию. Если такой исход единственный, то его и считают оптимальным. Если же таких исходов несколько, то среди них отбирают те, которые имеют максимальную оценку по следующему за важнейшим критерию. В результате такой процедуры всегда остается как правило один исход.
Упорядочим критерии по относительной важности. Например, следующим образом: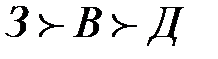 
(т.е. важнейший критерий — зарплата, следующий за ним по важности время поездки, наименее важный критерий длительность отпуска).
Максимальное значение по критерию Зарплата имеют вариант 7. Далее сравниваем эти варианты по второму по важности критерию Время поездки. Потом переходим к третьему критерию Длительность отпуска. Лучшим является вариант 7, который и является здесь оптимальным.
При упорядочении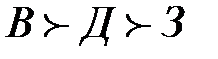 
оптимальным является вариант 6, а при упорядочении 
– оптимальным становится вариант 5.
Источник
Способы сужения Парето-оптимального множества
Выделение множества Парето многокритериальной задачи оптимизации часто не является удовлетворительным решением. Это связано с тем, что при достаточно большом исходном множестве вариантов множество Парето оказывается недопустимо большим для того, чтобы ЛПР было бы в состоянии осуществить выбор самостоятельно. Таким образом, выделение множества Парето можно рассматривать лишь как предварительный этап оптимизации, и налицо проблема дальнейшего сокращения этого множества.
Для выбора одной оптимальной стратегии из множества эффективных решений в каждой конкретной многокритериальной задаче необходимо использовать дополнительную информацию о цели операции, т.е. ту информацию, которая при задании векторного критерия осталась неформализованной и потому неиспользованной.
Наиболее логичным и последовательным представляется путь построения бинарного отношения предпочтения, более сильного, чем отношение Парето, позволяющего сузить множество выбираемых вариантов до приемлемых с точки зрения ЛПР размеров. Разумеется, для этого потребуется некоторая дополнительная информация, которую придётся получить от ЛПР. Это может быть информация о критериях, о самих сравниваемых вариантах и т.п. Задача, стоящая перед создателями методов, заключается в том, чтобы с помощью этой информации обосновать свои действия по сужению выбора и гарантировать ЛПР от того, чтобы ни один из вариантов, представляющих для него интерес, не был потерян в процессе оптимизации.
Необходимо отметить, что необоснованность сужения множества Парето является существенным недостатком многих методов многокритериальной оптимизации. Многокритериальная оптимизация: Математические аспекты /Б.А Березовский, Ю.М. Барышников и др. — М.: Наука, 1989. — 128 с.
Таким образом, общая методика исследования задач принятия решения на основе математического моделирования для МЗО может быть реализована в рамках одного из следующих подходов.
Первый подход. Для заданной многокритериальной задачи оптимизации находится множество её Парето-оптимальных решений, а выбор конкретного оптимального варианта из множества Парето-оптимальных предоставляется ЛПР.
Второй подход. Как уже было сказано выше, производится сужение множества Парето-оптимальных исходов (в идеале – до одного элемента) с помощью некоторых формализованных процедур, что облегчает окончательный исход для ЛПР. Отметим, что такое сужение может быть произведено только при наличии дополнительной информации о критериях или свойствах оптимального решения.
Рассмотрим некоторые простейшие способы сужения Парето-оптимального множества, акцентируя при этом внимание на необходимость дополнительной информации. Считаем, что задана многокритериальная задача оптимизации.
Указание верхних границ критериев. Дополнительная информация об оптимальном исходе XoptÎD в этом случае имеет вид
()
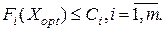
Число Ci рассматривается здесь как верхняя граница по i – му критерию.
Отметим, что указание верхних границ по критериям не может быть «извлечено» из математической модели задачи принятия решения; набор ограничений (C1, C2, , Cm) представляет собой дополнительную информацию, полученную от ЛПР.
Задача. Выбор места работы
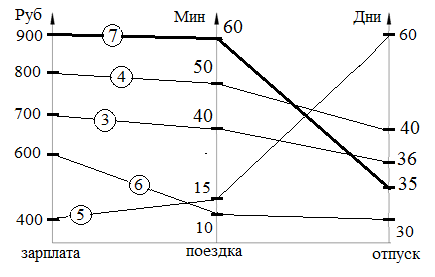
Предположим, что Вам предстоит выбрать место работы из девяти вариантов, представленных в табл.1. В качестве основных критериев взяты: зарплата З, длительность отпуска Д, время поездки на работу В. Из смысла задачи следует, что критерии З и Д следует максимизировать, а критерий В – минимизировать. Какой вариант является оптимальным?
| Варианты | Критерий | |
| Зарплата, (руб.) | Длительность отпуска, (дни) | Время поездки, (мин) |
Решение. Выделим вначале Парето-оптимальные варианты. Отбрасывая доминируемые по Парето варианты <1, 2, 8, 9>, получаем Парето-оптимальное множество <3, 4, 5, 6, 7>. При отсутствии информации об относительной важности рассматриваемых критериев, а также о каких-либо дополнительных свойствах оптимального решения дальнейшее сужение Парето-оптимального множества произвести нельзя. Тогда формальный анализ заканчивается указанием Парето-оптимального множества, и окончательный выбор оптимального варианта производится ЛПР из этих пяти вариантов на основе каких-то дополнительных соображений.
Рассмотрим теперь второй подход, который приводит к сужению Парето-оптимального множества на основе дополнительной информации, получаемой от ЛПР.
а) Указание нижних границ критериев. Наложим, например, следующие ограничения на оптимальное решение:
зарплата — не менее 600 рублей;
длительность отпуска — не менее 30 дней;
время поездки — не более 40 минут.
Варианты, удовлетворяющие этим дополнительным ограничения: <3, 6, 9>; из них оптимальными по Парето являются варианты 3 и 6. Остаётся сделать окончательный выбор между вариантами 3 и 6.
б) Субоптимизация. Пусть в качестве выделенного (главного, важнейшего) критерия выступает критерий зарплата; ограничения длительность отпуска — не менее 30 дней, время поездки — не более 40 минут. Отбросим варианты, которые не удовлетворяют данным ограничениям; остаются варианты: <2, 3, 5, 6, 9>. Из них максимальную зарплату имеет вариант 3. Этот вариант и будет оптимальным.
в) Лексикографическая оптимизация. Упорядочим критерии по относительной важности. Например, следующим образом: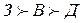 
(т.е. важнейший критерий — зарплата, следующий за ним по важности время поездки, наименее важный критерий длительность отпуска). Максимальное значение по критерию З имеют варианты 1 и 7. Далее сравниваем эти варианты по второму по важности критерию В. Так как время поездки для этих вариантов одинакова, переходим к третьему критерию Д; по критерию длительность отпуска лучшим является вариант 7, который и является здесь оптимальным.
Задание. Проверьте, что при упорядочении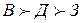 
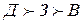
оптимальным является вариант 6, а при упорядочении 
– оптимальным становится вариант 5.
Методы ЭЛЕКТРА [1]
Группа методов (ЭЛЕКТРА 1, ЭЛЕКТРА 2, ЭЛЕКТРА 3) предложена профессором Б. Руа (Франция). В этих методах бинарное отношение предпочтения (более сильное, чем отношение Парето) строятся следующим образом.
Для каждого из m критериев (предполагаются, что критерии числовые) определяется вес – число, характеризующее важность соответствующего критерия. Для того чтобы определить, превосходит ли вариант X1 вариант X2, производятся следующие действия.
Множество критериев разбивается на три подмножества:
· критерии, по которым X1 превосходит X2;
· критерии, по которым X1 и X2 имеют одинаковые оценки;
· критерии, по которым X2 превосходит X1.
Далее определяется относительная важность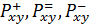 
каждого из этих подмножеств. Устанавливается некоторый порог c и считается, что вариант X1 превосходит X2 только в том случае, когда некоторая функция (называемая индексом согласия) удовлетворяет условию
f( 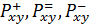)≥c (1)
Условие (1) является необходимым, но не достаточным условием превосходства X1 над X2. В некоторых методах ЭЛЕКТРА формулируется дополнительные условия, которые предназначены учитывать не только порядок следования оценок X1 над X2 по критериям, но и значения их разностей.
Проведём анализ описанного метода.
На первом этапе (во всех модификациях ЭЛЕКТРА) определяются веса критериев – положительные действительные числа, которые тем больше, чем важнее соответствующий критерий). Такой подход имеет существенный недостаток – неоднозначность определения весовых коэффициентов.
Существую ситуации, когда ЛПР сообщает информацию о критериях качественного типа. Например, при назначении весов критериям, по которым следует выбрать автомобиль: цена (критерий 1), важнее комфортности (критерий 2), а та, в свою очередь, важнее, чем скоростные качества (критерий 3) и внешний вид автомобиля (критерий 4). Кроме того, критерии 3 и 4 имеют одинаковую важность, а, рассматриваемые совместно, имею большую важность, чем критерий 1 (цена).
p1> p2>p3= p4, p3+ p4> p1.
Один из вариантов назначения весовых коэффициентов: p1=5; p2=4; p3=p4=3.
Множество критериев разбивается на три подмножества;
Далее определяется относительная важность 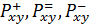, как сумма весов, входящих в них критериев.
В качестве условия (1) предлагается (ЭЛЕКТРА 1) взять выражение
Зам. Если мы выбрали нормированные весовые коэффициенты, то λi=pi и 
Рассмотрим пример. Пусть у нас имеются два решения X1 и X2, которые оцениваются по 5 критериям (F1, F2, F3, F4, F5):
Определяем весовые коэффициенты:
Литература
1. Многокритериальная оптимизация: Математические аспекты /Б.А Березовский, Ю.М. Барышников и др. – М.: Наука, 1989. – 128 с.
2. В.В. Розен. Математические модели принятия решений в экономике. Учебное пособие.– М.: Книжный дом «Университет», Высшая школа, 2002.– 288 с., ил.
Источник
