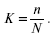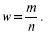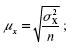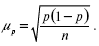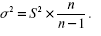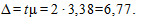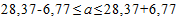Способы статистического наблюдения выборочное

Способы статистического наблюдения выборочное

1. Определение выборочного наблюдения

Статистические исследования очень трудоемки и дороги, поэтому возникла мысль о замене сплошного наблюдения выборочным.

Основная цель несплошного наблюдения состоит в получении характеристик изучаемой статистической совокупности по обследованной ее части.

Выборочное наблюдение – это метод статистического исследования, при котором обобщающие показатели совокупности устанавливаются только по отдельно взятой части на основе положений случайного отбора.

При выборочном методе изучению подвергается только некоторая часть изучаемой совокупности, при этом подлежащая изучению статистическая совокупность называется генеральной совокупностью.

Выборочной совокупностью или просто выборкой можно называть отобранную из генеральной совокупности часть единиц, которая будет подвергаться статистическому исследованию.

Значение выборочного метода: при минимальной численности исследуемых единиц проведение статистического исследования будет происходить в более короткие промежутки времени и с наименьшими затратами средств и труда.

В генеральной совокупности доля единиц, которая обладает изучаемым признаком, называется генеральной долей (обозначается р), а средняя величина изучаемого варьирующего признака – это генеральная средняя (обозначается х).

В выборочной совокупности долю изучаемого признака называют выборочной долей, или частью (обозначается w), средняя величина в выборке – это выборочная средняя.

Если в период обследования будут соблюдены все правила его научной организации, то выборочный метод даст довольно точны результаты, и поэтому данный метод целесообразно применять для проверки данных сплошного наблюдения.

Этот метод получил широкое распространение в государственной и вневедомственной статистике, потому что при исследовании минимальной численности изучаемых единиц позволяет тщательно и точно провести исследование.

Изучаемая статистическая совокупность состоит из единиц с варьирующими признаками. Состав выборочной совокупности может отличаться от состава генеральной совокупности, это расхождение между характеристиками выборки и генеральной совокупности составляет ошибку выборки.

Ошибки, свойственные выборочному наблюдению, характеризуют размер расхождения между данными выборочного наблюдения и всей совокупности. Ошибки, возникающие в ходе выборочного наблюдения, называются ошибками репрезентативности и делятся на случайные и систематические.

Если выборочная совокупность недостаточно точно воспроизводит всю совокупность из–за несплошного характера наблюдения, то это называют случайными ошибками, и их размеры определяются с достаточной точностью на основании закона больших чисел и теории вероятностей.

Систематические ошибки возникают в результате нарушения принципа случайности отбора единиц совокупности для наблюдения.

2. Виды и схемы отбора

Размер ошибки выборки и методы ее определения зависят от вида и схемы отбора.

Различают четыре вида отбора совокупности единиц наблюдения:

4) серийный (гнездовой).

Случайный отбор – наиболее распространенный способ отбора в случайной выборке, его еще называют методом жеребьевки, при нем на каждую единицу статистической совокупности заготовляется билет с порядковым номером.

Далее в случайном порядке отбирается необходимое количество единиц статистической совокупности. При этих условиях каждая из них имеет одинаковую вероятность попасть в выборку, например тиражи выигрышей, когда из общего количества выпущенных билетов в случайном порядке наугад отбирается определенная часть номеров, на которые приходятся выигрыши. При этом всем номерам обеспечивается равная возможность попасть в выборку.

Механический отбор – это способ, когда вся совокупность разбивается на однородные по объему группы по случайному признаку, потом из каждой группы берется только одна единица Все единицы изучаемой статистической совокупности предварительно располагаются в определенном порядке, но в зависимости от объема выборки механически через определенный интервал отбирается необходимое количество единиц.

Типический отбор – это способ, при котором исследуемая статистическая совокупность разбивается по существенному, типическому признаку на качественно однородные, однотипные группы, затем из каждой этой группы случайным способом отбирается определенное количество единиц, пропорциональное удельному весу группы во всей совокупности.

Типический отбор дает более точные результаты, так как при нем в выборку попадают представители всех типических групп.

Серийный (гнездовой) отбор. Отбору подлежат целые группы (серии, гнезда), отобранные случайным или механическим способом. По каждой такой группе, серии проводится сплошное наблюдение, а результаты переносятся на всю совокупность.

Точность выборки зависит и от схемы отбора. Выборка может быть проведена по схеме повторного и бесповторного отбора.

Повторный отбор. Каждая отобранная единица или серия возвращается во всю совокупность и может вновь попасть в выборку Это так называемая схема возвращенного шара.

Бесповторный отбор. Каждая обследованная единица изымается и не возвращается в совокупность, поэтому она не попадает в повторное обследование. Эта схема получила название невозвращенного шара.

Бесповторный отбор дает более точные результаты, потому что при одном и том же объеме выборки наблюдение охватывает большее количество единиц изучаемой совокупности.

Комбинированный отбор может проходить одну или несколько ступеней. Выборка называется одноступенчатой, если отобранные однажды единицы совокупности подвергаются изучению.

Выборка называется многоступенчатой, если отбор совокупности проходит по ступеням, последовательным стадиям, причем каждая ступень, стадия отбора имеет свою единицу отбора.

Многофазная выборка – на всех ступенях выборки сохраняется одна и та же единица отбора, но проводится несколько стадий, фаз выборочных обследований, которые различаются между собой широтой программы обследования и объемом выборки.

Характеристики параметров генеральной и выборочной совокупностей обозначаются следующими символами:

N – объем генеральной совокупности;

n – объем выборки;

X – генеральная средняя;

х – выборочная средняя;

р – генеральная доля;

w – выборочная доля;

? 2 – генеральная дисперсия (дисперсия признака в генеральной совокупности);

? 2 – выборочная дисперсия того же признака;

?– среднее квадратическое отклонение в генеральной совокупности;

?– среднее квадратическое отклонение в выборке.

3. Ошибки выборки

Каждая единица при выборочном наблюдении должна иметь равную с другими возможность быть отобранной – это является основой собственнослучайной выборки.

Собственнослучайная выборка – это отбор единиц из всей генеральной совокупности посредством жеребьевки или другим подобным способом.

Принципом случайности является то, что на включение или исключение объекта из выборки не может повлиять любой фактор, кроме случая.

Доля выборки – это отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности:

Собственнослучайный отбор в чистом виде является исходным среди всех других видов отбора, в нем заключаются и реализуются основные принципы выборочного статистического наблюдения.

Два основных вида обобщающих показателей, которые используют в выборочном методе – это средняя величина количественного признака и относительная величина альтернативного признака.

Выборочная доля (w), или частность, определяется отношением числа единиц, обладающих изучаемым признаком m, к общему числу единиц выборочной совокупности (n):

Для характеристики надежности выборочных показателей различают среднюю и предельную ошибки выборки.

Ошибка выборки, ее еще называют ошибкой репрезентативности, представляет собой разность соответствующих выборочных и генеральных характеристик:

1) для средней количественного признака:

2) для доли (альтернативного признака):

Только выборочным наблюдениям присуща ошибка выборки

Выборочная средняя и выборочная доля – это случайные величины, принимающие различные значения в зависимости от единиц изучаемой статистической совокупности, которые попали в выборку. Соответственно ошибки выборки – тоже случайные величины и также могут принимать различные значения. Поэтому определяют среднюю из возможных ошибок – среднюю ошибку выборки.

Средняя ошибка выборки определяется объемом выборки: чем больше численность при прочих равных условиях, тем меньше величина средней ошибки выборки. Охватывая выборочным обследованием все большее количество единиц генеральной совокупности, все более точно характеризуем всю генеральную совокупность.

Средняя ошибка выборки зависит от степени варьирования изучаемого признака, в свою очередь степень варьирования характеризуется дисперсией ? 2 или w(l – w) – для альтернативного признака. Чем меньше вариация признака и дисперсия, тем меньше средняя ошибка выборки, и наоборот.

При случайном повторном отборе средние ошибки теоретически рассчитывают по следующим формулам:

1) для средней количественного признака:

где ? 2 – средняя величина дисперсии количественного признака.

2) для доли (альтернативного признака):

Так как дисперсия признака в генеральной совокупности ? 2 точно неизвестна, на практике пользуются значением дисперсии S 2 , рассчитанным для выборочной совокупности на основании закона больших чисел, согласно которому выборочная совокупность при достаточно большом объеме выборки достаточно точно воспроизводит характеристики генеральной совокупности.

Формулы средней ошибки выборки при случайном повторном отборе следующие. Для средней величины количественного признака: генеральная дисперсия выражается через выборную следующим соотношением:

где S 2 – значение дисперсии.

Механическая выборка – это отбор единиц в выборочную совокупность из генеральной, которая разбита по нейтральному признаку на равные группы; производится так, что из каждой такой группы в выборку отбирается лишь одна единица.

При механическом отборе единицы изучаемой статистической совокупности предварительно располагают в определенном порядке, после чего отбирают заданное число единиц механически через определенный интервал. При этом размер интервала в генеральной совокупности равен обратному значению доли выборки.

При достаточно большой совокупности механический отбор по точности результатов близок к собственнослучайному Поэтому для определения средней ошибки механической выборки используют формулы собственнослучайной бесповторной выборки.

Для отбора единиц из неоднородной совокупности применяется так называемая типическая выборка, используется, когда все единицы генеральной совокупности можно разбить на несколько качественно однородных, однотипных групп по признакам, от которых зависят изучаемые показатели.

Затем из каждой типической группы собственнослучайной или механической выборкой производится индивидуальный отбор единиц в выборочную совокупность.

Типическая выборка обычно применяется при изучении сложных статистических совокупностей.

Типическая выборка дает более точные результаты. Типизация генеральной совокупности обеспечивает репрезентативность такой выборки, представительство в ней каждой типологической группы, что позволяет исключить влияние межгрупповой дисперсии на среднюю ошибку выборки. Поэтому при определении средней ошибки типической выборки в качестве показателя вариации выступает средняя из внутригрупповых дисперсий.

Серийная выборка предполагает случайный отбор из генеральной совокупности равновеликих групп для того, чтобы в таких группах подвергать наблюдению все без исключения единицы.

Поскольку внутри групп (серий) обследуются все без исключения единицы, средняя ошибка выборки (при отборе равновеликих серий) зависит только от межгрупповой (межсерийной) дисперсии.

4. Способы распространения выборочных результатов на генеральную совокупность

Характеристика генеральной совокупности на основе выборочных результатов – это конечная цель выборочного наблюдения.

Выборочный метод применяется для получения характеристик генеральной совокупности по определенным показателям выборки. В зависимости от целей исследования это осуществляется прямым пересчетом показателей выборки для генеральной совокупности или методом расчета поправочных коэффициентов.

Способ прямого пересчета в том, что при нем показатели выборочной доли w или средней х распространяются на генеральную совокупность с учетом ошибки выборки.

Способ поправочных коэффициентов применяется, когда целью выборочного метода является уточнение результатов сплошного учета. Данный способ используется при уточнении данных ежегодных переписей скота у населения.

Источник

Выборочный метод статистического наблюдения

Одним из наиболее распространенных в статистике методов несплошного наблюдения является выборочный метод, при котором отбор подлежащих обследованию единиц совокупности осуществляется в случайном порядке. Совокупность, из которой производится отбор, называется генеральной, а ее показатели — генеральными показателями. Совокупность отобранных единиц называется выборочной совокупностью, или просто выборкой, а обобщающие показатели выборки называются выборочными показателями.

Основная задача выборочного метода состоит в том, чтобы на основе характеристик выборочной совокупности получить достоверные характеристики генеральной совокупности. Правомерность распространения характеристик, рассчитанных по выборке, на всю генеральную совокупность и обеспечение в каждом конкретном наблюдении приемлемой ошибки репрезентативности научно обоснована в теории вероятностей и математической статистике.

Выборочное наблюдение является важнейшим источником первичных статистических данных в тех случаях, когда учет всех единиц изучаемой совокупности невозможен по организационным или техническим причинам или требует больших финансовых затрат. Кроме того, выборочный метод приводит к экономии времени и средств в результате уменьшения объема работы и сокращения ошибок, происходящих при регистрации. Ведь при обследовании, скажем, 10-15% единиц совокупности будет затрачено гораздо меньше средств и времени, а результаты могут быть представлены быстрее и будут более актуальными. Фактор времени важен для статистического исследования в области криминальных явлений, особенно в условиях постоянно изменяющейся социально-экономической ситуации. Еще один фактор превращения выборочного наблюдения в важнейший источник социально-правовой информации — возможность его использования в целях уточнения и для разработки данных сплошного обследования. Выборочная разработка данных сплошного наблюдения связана с потребностью представления оперативных предварительных итогов обследования. Кроме того, при обобщении данных сплошного учета (например, карточек единого учета преступлений) невозможно вести сплошную разработку по всем сочетаниям рассматриваемых признаков. В этих условиях выборочный метод позволяет получить необходимые сведения приемлемой точности. В судебной статистике выборочный метод в основном используется при обобщении судебной практики.

Преимущества выборочного наблюдения можно реализовать, если он организован в соответствии с принципами теории выборочного метода:

1) выбор единиц наблюдения должен быть случайным, т.е. каждая единица изучаемой совокупности должна иметь равную вероятность попасть в выборку;

2) выбор должен быть произведен из всех частей изучаемой совокупности (например, из всех категорий гражданских дел);

3) число единиц, взятых для выборочного обследования, должно быть достаточным.

Соблюдение этих принципов позволяет получить гарантию репрезентативности (представительности) выборочной совокупности. Репрезентативность означает, что объекты выборки достаточно хорошо представляют генеральную совокупность.

Выборочное наблюдение достигается в результате применения научно обоснованных способов формирования выборочной совокупности, в зависимости от которых выборка может быть:

Собственно случайная выборка состоит в том, что выборочная совокупность образуется в результате случайного (непреднамеренного) отбора отдельных единиц из генеральной совокупности. Важным условием репрезентативности собственно случайной выборки является то, что каждой единице генеральной совокупности предоставляется равная возможность попасть в выборочную совокупность. Собственно случайная выборка может быть осуществлена по схемам повторного и бесповторного отбора. При повторном отборе единица, попавшая в выборку, после регистрации снова возвращается в генеральную совокупность и при отборе очередной единицы она снова может попасть в выборку. Общая численность единиц генеральной совокупности в процессе выборки остается неизменной. При бесповторном отборе единица совокупности, попавшая в выборку, в генеральную совокупность не возвращается и, таким образом, не имеет шансов быть повторно отобранной в данную выборку. Численность единиц генеральной совокупности в процессе исследования в этом случае сокращается.

На практике для организации собственно случайной выборки часто используют таблицу случайных чисел или генератор случайных чисел. В Microsoft Excel выборка формируется на основе генератора случайных чисел.

Механическая выборка заключается в том, что генеральная совокупность делится на равные по численности группы, количество которых должно быть равно желаемому объему выборки, а затем из каждой группы отбирается одна единица с каким-либо одним и тем же порядковым номером внутри группы. Обычно порядковый номер внутри группы принимается равным обратной величине доли выборки. Например, генеральная совокупность состоит из N = 1000 статистических карточек на осужденных, а выборка определяется равной n = 100 единицам. Тогда доля выборки будет равна 100 : 1000 = 1/10 и, следовательно, из каждой группы будет отбираться каждая 10-я статистическая карточка. Механическая выборка применяется в случаях, когда генеральная совокупность каким-либо образом упорядочена, т.е. имеется определенная последовательность в расположении единиц совокупности (номера учреждений уголовно-исполнительной системы — по регионам; номера уголовных дел — в зависимости от подследственности и т.п.).

Типическая выборка применяется в случае изучения совокупности, неоднородной по одному или нескольким существенным признакам, и основана на отборе единиц не из всей генеральной совокупности в целом, а из ее типических групп. Например, при обследовании учреждений уголовно-исполнительной системы такими типическими группами могут быть виды исправительных колоний в зависимости от режима, возраста заключенных и т.д. Для получения типической выборки генеральную совокупность предварительно делят на внутренне однородные группы (страты), соответствующие тем типам единиц, которые представлены в этой совокупности. Непосредственный отбор единиц из типических групп производится в виде собственно случайного или механического отбора в количестве, пропорциональном численности данной группы в генеральной совокупности.

Серийная выборка используется, когда единицы совокупности объединены в небольшие группы или серии, и формируется с помощью собственно случайного либо механического отбора серий, внутри которых производится сплошное обследование единиц. Серии (гнезда) состоят из единиц, связанных между собой территориально, организационно или, наконец, по времени (сотрудники отдела, судьи одного суда, исковые заявления, поступившие в конкретном месяце и т.п.).

Комбинированная выборка предполагает применение на практике комбинации перечисленных выше способов отбора элементов генеральной совокупности. В частности, можно комбинировать типическую и серийную выборки, когда серии отбираются в установленном порядке из нескольких типических групп. Например, при выборочном исследовании гражданских дел такими типическими группами являются суды разного уровня — судебные участки мировых судей, районные суды, суды областного уровня. При этом судебный орган будет являться серией, в которой ведется сплошное статистическое наблюдение.

Основными выборочными показателями являются выборочная доля, выборочное среднее и выборочная дисперсия.

Выборочная доля 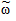определяется отношением числа единиц выборки m, обладающих изучаемым признаком, к общему числу единиц выборочной совокупности n, т.е.

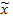
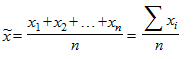
Выборочное среднее количественного признака определяется по данным выборки по формуле:

,

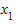
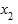
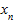
где , , . , — выборочные значения; n — число выбранных единиц совокупности.

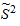
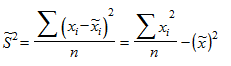
Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их выборочного среднего. Она является характеристикой рассеяния значений количественного признака вокруг его среднего значения. Выборочная дисперсия определяется по формуле:

.

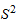
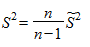
Наряду с выборочной дисперсией в статистике используется так называемая исправленная выборочная дисперсия , которая связана с обычной дисперсией следующим соотношением:

.

Введение исправленной выборочной дисперсии связано с тем, что для малых выборок ее использование приводит к лучшим оценкам характеристик генеральной совокупности.

В целом же следует отметить, что все приведенные выше выборочные характеристики являются оценками для соответствующих генеральных характеристик.

Выборочный метод, обладая несомненным достоинством, состоящим в возможности значительно сократить время на получение основных статистических характеристик, приводит к появлению ошибки репрезентативности и уменьшению гарантии получения истинных характеристик генеральной совокупности. Расхождения между характеристиками выборочной и генеральной совокупностей измеряются средней квадратической ошибкой выборки 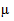. В математической статистике доказывается, что величина средней квадратической ошибки собственно случайной выборки определяется формулами:

а) в случае повторной выборки:

;

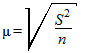
б) в случае бесповторной выборки:

,

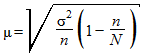
где 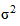— дисперсия генеральной совокупности, n — объем выборки; N — объем генеральной совокупности.

Поскольку на практике дисперсия генеральной совокупности неизвестна, то для определения средней квадратической ошибки выборки используются следующие приближенные формулы:

а) в случае повторной выборки:

;

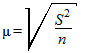
б) в случае бесповторной выборки

,

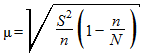
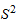
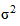
где — оценка генеральной дисперсии .

В теории статистики разработаны формулы расчета средней квадратической ошибки выборки применительно к каждому из перечисленных выше способов ее отбора. Если величина этой ошибки рассчитывается с учетом уровня доверительной вероятности, с которой гарантируется достоверность результата, то она называется предельной ошибкой выборки и определяется по формуле:

,

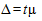
где t — коэффициент доверия, зависящий от уровня доверительной вероятности.

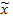
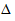
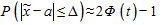
Из центральной предельной теоремы теории вероятностей следует, что при достаточно большом объеме выборки доверительная вероятность того, что расхождение между выборочным средним и генеральным средним значением а количественного признака не превзойдет по абсолютной величине равна:

,

где Р(.) — доверительная вероятность неравенства, стоящего в скобках; Ф(t) — функция стандартного нормального распределения, значения которой табулированы (приложение 2, табл. 2).

Таким образом, величина коэффициента доверия t определяется по таблице в зависимости от того, с какой доверительной вероятностью надо гарантировать результаты выборочного обследования. Например, если мы хотим гарантировать результаты выборочного обследования с доверительной вероятностью 0,9545, т.е. 2Ф(t) — 1 = 0,9545, то Ф(t) = 0,97725 и из табл. 2 приложения 2 получим t = 2.

Приведем наиболее часто употребляемые уровни доверительной вероятности и соответствующие значения t (табл. 1).

Коэффициент доверия t	1,0	1,96	2,0	2,58	3,0
Уровень доверительной вероятности р	0,6827	0,9500	0,9545	0,9901	0,9973

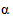
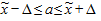
Расчет средней и предельной ошибок выборки позволяет определить возможные пределы, в которых будут находиться характеристики генеральной совокупности с заданной доверительной вероятностью. Например, с учетом предельной ошибки выборки для генеральной средней количественного признака такие пределы определяются по следующей формуле:

,

где 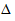зависит от вероятности того, что средняя величина генеральной совокупности окажется в заданных пределах.

Замечание. Наряду с определением ошибок выборки и пределов для генеральной средней количественного признака, эти же величины могут быть определены для показателя качественного признака — доли признака. При вычислении указанных выше характеристик для доли признака особенности расчета связаны с определением дисперсии доли, оценка которой вычисляется по формуле:

,

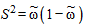
где 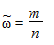, причем m — число единиц выборки, обладающих данным признаком, а n — объем выборки.

В процессе любого выборочного наблюдения возникает вопрос о том, каков должен быть объем выборки, чтобы ошибка репрезентативности с заданной доверительной вероятностью не вышла за приемлемые для данного наблюдения границы, и в то же время чтобы этот объем не был избыточным для исключения неоправданных затрат на проведение наблюдения. Минимальный необходимый объем выборки рассчитывается для повторного и бесповторного отбора по формулам, которые алгебраически выводятся из рассмотренных ранее формул для расчета ошибок выборки. Так, необходимая численность собственно случайной повторной выборки выражается формулой:

,

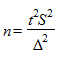
а объем собственно случайной бесповторной выборки рассчитывается по формуле:

,

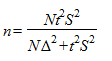
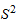
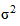
где N — объем генеральной совокупности, а — оценка генеральной дисперсии .

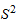
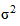
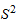
Затруднительным моментом применения приведенных формул на практике является нахождение оценки генеральной дисперсии , так как при ее расчете уже необходимо знать объем выборки n. Поэтому для нахождения оценки пользуются или материалами предыдущих исследований или проводят пробное (пилотное) обследование, по результатам которого получают данную оценку генеральной дисперсии.

Пример. Для определения среднего срока нахождения гражданского дела в суде проведено 5%-ное выборочное обследование из 1200 дел. При собственно-случайной бесповторной выборке получены следующие данные о сроках нахождения в производстве суда гражданских дел (в днях): 15, 44, 22, 21, 16, 31, 42, 32, 23, 27, 5, 6, 40, 36, 10, 5, 41, 11, 22, 33, 31, 42, 10, 6, 5, 3, 14, 3, 5, 12, 43, 35, 27, 4, 6, 54, 74, 3, 1, 5, 44, 63, 12, 67, 57, 63, 94, 5, 5, 30, 3, 34, 34, 5, 6, 121, 44, 30, 100, 20.

1. С доверительной вероятностью 0,9545 определить пределы среднего срока нахождения в производстве суда гражданских дел.

2. Считая полученную выборку пробной для нахождения оценки генеральной дисперсии, найти такой необходимый объем выборки, чтобы предельная ошибка выборки не превышала 3 дней с доверительной вероятностью 0,9545.

Решение. Вначале на основе имеющихся данных определим выборочную среднюю и дисперсию. Так как n = 60, то

;

.

.

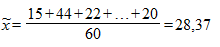
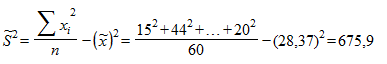
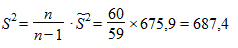
Вычисляем теперь среднюю ошибку выборки:

.

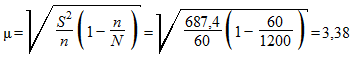
Тогда предельная ошибка выборки при доверительной вероятности р = 0,9545 равна

Следовательно, пределы генеральной средней:

или .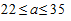

Таким образом, с доверительной вероятностью 0,9545 можно утверждать, что средний срок нахождения в производстве суда гражданских дел колеблется от 22 до 35 дней.

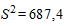
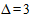
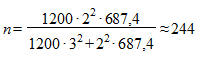
Для расчета необходимого объема выборки воспользуемся формулой для собственно случайной бесповторной выборки и, подставляя N = 1200, t = 2, , , получим

.

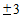
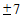
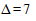
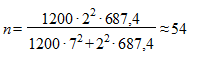
Таким образом, если из 1200 имеющихся дел мы выберем для наблюдения 244 дела и рассчитаем по данной выборке среднее значение изучаемого признака (срок нахождения дела в производстве), то с вероятностью 0,9545 можно будет утверждать, что это значение отклонится от генеральной средней не более, чем на дня. Если же такая точность не обязательна и при таком же уровне доверительной вероятности нас устроит предельная ошибка, например, дней ( ), то необходимый объем выборки будет значительно меньше:

.

Источник