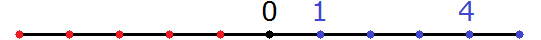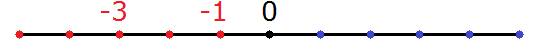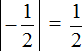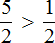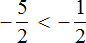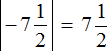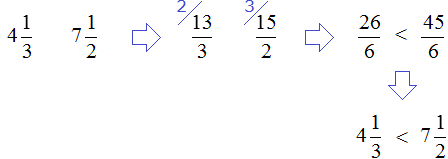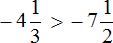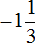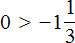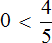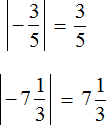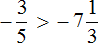Способы сравнения рациональных чисел

Сравнение рациональных чисел, правила, примеры.

В этой статье дается подробный обзор наиболее важных моментов, касающихся сравнения рациональных чисел. Если знаки сравниваемых чисел различны, то можно сразу сказать, какое число больше, а какое меньше, поэтому в самом начале мы разберем правило сравнения рациональных чисел с разными знаками. Дальше остановимся на сравнении нуля с другим рациональным числом. После этого подробно остановимся на сравнении положительных рациональных чисел. Наконец, перейдем к правилу сравнения отрицательных рациональных чисел. Теорию будем разбавлять решениями характерных примеров.

Навигация по странице.

Сравнение рациональных чисел с разными знаками

Проще всего выполнить сравнение двух рациональных чисел, имеющих разные знаки. При этом используется правило сравнения чисел с разными знаками: любое положительное число больше любого отрицательного, а любое отрицательное число меньше положительного.

Например, из двух рациональных чисел 5/7 и −0,25 больше число 5/7 , так как оно положительное, а меньше число −0,25 , так как оно отрицательное. Еще пример: отрицательное рациональное число меньше, чем положительное рациональное число 0,000(1) .

Сравнение рационального числа с нулем

Очень просто проводится сравнение нуля с рациональным числом, отличным от нуля. При этом справедливо правило: любое положительное число больше нуля, а любое отрицательное число меньше нуля.

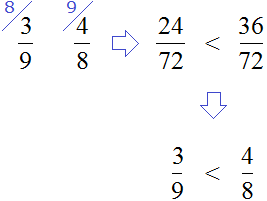
Приведем пару примеров сравнения рационального числа с нулем. Число 4/9 больше, чем 0 , так как 4/9 – положительное число, с другой стороны 0 меньше, чем 4/9 . Еще пример: число 0 больше, чем отрицательное рациональное число −45,5 , с другой стороны число −45,5 меньше нуля.

Также нужно сказать, про сравнение нуля с нулем: нуль равен нулю, то есть, 0=0 .

Здесь нужно заметить, что число нуль может быть записано в виде, отличном от 0 . Действительно, числу 0 отвечает любая запись вида 0/n , где n – любое натуральное число, или записи 0,0, 0,00, … , вплоть до 0,(0) . То есть, например, при сравнении двух рациональных чисел, записи которых имеют вид 0,00 и 0/3 , заключаем, что они равны, так как эти записи отвечают числам 0 и 0 соответственно.

Сравнение положительных рациональных чисел

Сравнение положительных рациональных чисел следует начинать со сравнения их целых частей. При этом используется следующее правило: больше то число, целая часть которого больше, а меньше то число, целая часть которого меньше.

Какое из рациональных чисел 0,76 и больше?

Сравниваемые рациональные числа положительные, причем достаточно очевидно, что целая часть числа 0,76 , равная нулю, меньше целой части числа , равной двум (при необходимости смотрите сравнение целых чисел). Следовательно, , значит, из двух исходных чисел больше число .

.

Нюансы в применении указанного выше правила могут возникнуть лишь тогда, когда одним из сравниваемых чисел является периодическая десятичная дробь с периодом 9 , о чем мы упоминали в разделе равные и неравные десятичные дроби.

Сравните рациональные числа 15 и 14,(9) .

Периодическая дробь с периодом 9 вида 14,(9) является лишь одной из форм записи числа 15 . То есть, 15=14,(9) .

исходные рациональные числа равны.

Если же целые части сравниваемых рациональных чисел равны, итоговый результат сравнения поможет получить сравнение дробных частей. Дробную часть рационального числа всегда можно представить в виде обыкновенной дроби m/n , а также в виде конечной или периодической десятичной дроби. Таким образом, сравнение дробных частей двух положительных рациональных чисел всегда можно свести к сравнению обыкновенных дробей или к сравнению десятичных дробей. В итоге из двух положительных рациональных чисел с равными целыми частями больше то, дробная часть которого больше, а меньше то – дробная часть которого меньше.

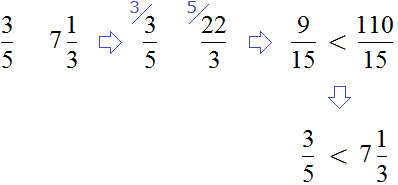
Проведите сравнение положительных рациональных чисел 3,7 и .

Очевидно, целые части сравниваемых рациональных чисел равны 3=3 . Переходим к сравнению дробных частей, то есть, к сравнению чисел 0,7 и 2/3 .

Покажем два способа.

В первом из осуществим перевод десятичной дроби в обыкновенную: 0,7=7/10 . Приходим к сравнению обыкновенных дробей 7/10 и 2/3 . После их приведения к общему знаменателю 30 получаем , откуда следует, что и . Следовательно, .

Во втором варианте решения выполним перевод обыкновенной дроби в десятичную, имеем . Так от сравнения 0,7 и 2/3 мы пришли к сравнению десятичных дробей 0,7 и 0,(6) , результат которого таков: 0,7>0,(6) . Следовательно, и .

Очевидно, оба способа нас привели к одинаковому результату сравнения исходных рациональных чисел.

.

Если равны и целые и дробные части сравниваемых положительных рациональных чисел, то эти числа равны.

Сравните числа 4,5 и .

Очевидно, целые части чисел равны. Дробная часть числа 4,5 равна 0,5 , перевод этой десятичной дроби в обыкновенную дает 1/2 . Таким образом, дробные части исходные чисел тоже равны. Следовательно, исходные рациональные числа равны.

Закончим этот пункт следующим утверждением: если записи сравниваемых чисел полностью совпадают, то эти числа равны. Действительно, в этом случае равны и целые части и дробные части сравниваемых чисел. Например, равными являются рациональные числа 5,698 и 5,698 , также равны числа и .

Сравнение отрицательных рациональных чисел

Сравнение отрицательных рациональных чисел подчиняется правилу сравнения отрицательных чисел: из двух отрицательных чисел больше то, модуль которого меньше, и меньше то, модуль которого больше.

Это правило сводит сравнение отрицательных рациональных чисел к сравнению положительных рациональных чисел, разобранному в предыдущем пункте.

Сравните числа −15,2 и .

Сравниваемые рациональные числа отрицательные. Модули чисел равны соответственно 15,2 и 5/9 . Целая часть числа 15,2 равна 15 , и она больше целой части числа 5/9 , равной нулю. Следовательно, . Тогда, согласно правилу сравнения отрицательных чисел, число −15,2 меньше числа , так как модуль числа −15,2 больше модуля числа .

.

Выполните сравнение отрицательных рациональных чисел −1,11 и .

Модули сравниваемых чисел равны 1,11 и соответственно. Очевидно, их целые части равны. Сравним дробные части, то есть, сравним 0,11 и 4/25 . Так как 0,11=11/100 и 4/25=16/100 , а , то , следовательно, . Тогда . На этом сравнение отрицательных рациональных чисел завершено.

.

Источник

Сравнение рациональных чисел

Расположение точек на числовой оси позволяет наглядно сравнивать между собой числа.

Напомним, что если координатная прямая изображена горизонтально, то положительные числа изображаются точками правее 0 , а отрицательные — левее 0 . В этом случае, если положительные числа отметить точками на этой прямой, то большему из двух чисел будет соответствовать точка, расположенная на числовой оси правее, а меньшему — точка, расположенная на координатной прямой левее.

Из двух чисел на координатной прямой больше то, которое расположено правее, а меньше то, которое расположено левее.

Это означает, что при сравнении рациональных чисел:

• любое положительное число больше нуля и больше любого отрицательного числа;
• любое отрицательное число меньше нуля и меньше любого положительного числа.

Сравнивать рациональные числа удобно с помощью понятия модуля.

Большее из двух положительных чисел изображается точкой, расположенной на координатной прямой правее, то есть дальше от начала отсчёта. Значит, это число имеет больший модуль.

Из двух положительных чисел больше то, чей модуль больше.

При сравнении двух отрицательных чисел большее будет расположено правее, то есть ближе к началу отсчёта. Значит, его модуль (длина отрезка от нуля до числа) будет меньше.

Из двух отрицательных чисел больше то, модуль которого меньше.

Пример. Сравнить числа « −6 » и « −12 .

Точка, соответствующая числу « −6 » расположена ближе к началу отсчёта, чем точка, соответствующая числу « −12 ».

Источник

Сравнение рациональных чисел

Продолжаем изучать рациональные числа. В данном уроке мы научимся сравнивать их.

Из предыдущих уроков мы узнали, что чем правее число располагается на координатной прямой, тем оно больше. И соответственно, чем левее располагается число на координатной прямой, тем оно меньше.

Например, если сравнивать числа 4 и 1, то можно сразу ответить, что 4 больше чем 1. Это вполне логичное утверждение и каждый с этим согласится.

В качестве доказательства можно привести координатную прямую. На ней видно, что четвёрка лежит правее единицы

Для этого случая есть и правило, которое при желании можно использовать. Выглядит оно следующим образом:

Из двух положительных чисел больше то число, модуль которого больше.

Чтобы ответить на вопрос какое число больше, а какое меньше, сначала нужно найти модули этих чисел, сравнить эти модули, а потом уже ответить на вопрос.

Например, сравним те же числа 4 и 1, применяя вышеприведенное правило

Находим модули чисел:

Сравниваем найденные модули:

Отвечаем на вопрос:

Для отрицательных чисел существует другое правило, выглядит оно следующим образом:

Из двух отрицательных чисел больше то число, модуль которого меньше.

Например, сравним числа −3 и −1

Находим модули чисел

Сравниваем найденные модули:

Отвечаем на вопрос:

Нельзя путать модуль числа с самим числом. Частая ошибка многих новичков. К примеру, если модуль числа −3 больше, чем модуль числа −1, это не означает, что число −3 больше, чем число −1.

Число −3 меньше, чем число −1 . Это можно понять, если воспользоваться координатной прямой

Видно, что число −3 лежит левее, чем −1 . А мы знаем, что чем левее, тем меньше.

Если сравнивать отрицательное число с положительным, то ответ будет напрашиваться сам. Любое отрицательное число будет меньше любого положительного числа. Например, −4 меньше, чем 2

Мы рассмотрели в качестве примера целые числа, вида −4, −3 −1, 2. Сравнить такие числа, а также изобразить на координатной прямой не составляет особого труда.

Намного сложнее сравнивать другие виды чисел, такие как обыкновенные дроби, смешанные числа и десятичные дроби, некоторые из которых являются отрицательными. Здесь уже в основном придётся применять правила, потому что точно изобразить такие числа на координатной прямой не всегда возможно. В некоторых случаях, число надо будет видоизменять, чтобы сделать его более простым для сравнения и восприятия.

Пример 1. Сравнить рациональные числа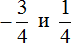

Итак, требуется сравнить отрицательное число с положительным. Любое отрицательное число меньше любого положительного числа. Поэтому не теряя времени отвечаем, что 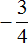меньше, чем

Пример 2. Сравнить рациональные числа 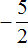и

Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то, модуль которого меньше.

Находим модули чисел:

Сравниваем найденные модули:

Согласно правилу, из двух отрицательных чисел больше то число, модуль которого меньше. Значит рациональное больше, чем , потому что модуль числа меньше, чем модуль числа

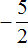
Пример 3. Сравнить числа 2,35 и

Требуется сравнить положительное число с отрицательным. Любое положительное число больше любого отрицательного числа. Поэтому не теряя времени отвечаем что 2,35 больше, чем

2,35 >

Пример 4. Сравнить рациональные числа 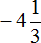и

Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то число, модуль которого меньше.

Находим модули чисел:

Сравниваем найденные модули. Но сначала приведём их к понятному виду, чтобы проще было сравнить, а именно переведём в неправильные дроби и приведём к общему знаменателю

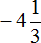
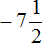
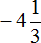
Согласно правилу, из двух отрицательных чисел больше то число, модуль которого меньше. Значит рациональное больше, чем , потому что модуль числа меньше, чем модуль числа

Пример 5. Сравнить рациональные числа 0 и

Требуется сравнить ноль с отрицательным числом. Ноль больше любого отрицательного числа, поэтому не теряя времени отвечаем, что 0 больше, чем

Пример 6. Сравнить рациональные числа 0 и

Требуется сравнить ноль с положительным числом. Ноль меньше любого положительного числа, поэтому не теряя времени отвечаем, что 0 меньше, чем

Пример 7. Сравнить рациональные числа 4,53 и 4,403

Требуется сравнить два положительных числа. Из двух положительных чисел больше то число, модуль которого больше.

Сделаем в обеих дробях количество цифр после запятой одинаковым. Для этого в дроби 4,53 припишем в конце один ноль

Далее применим правило сравнения положительных чисел.

Находим модули чисел

Сравниваем найденные модули:

Согласно правилу, из двух положительных чисел больше то число, модуль которого больше. Значит рациональное число 4,53 больше, чем 4,403 потому что модуль числа 4,53 больше, чем модуль числа 4,403

Пример 8. Сравнить рациональные числа 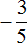и

Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то число, модуль которого меньше.

Находим модули чисел:

Сравниваем найденные модули. Но сначала приведём их к понятному виду, чтобы проще было сравнить, а именно переведём смешанное число 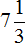в неправильную дробь, затем приведём обе дроби к общему знаменателю:

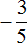
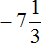
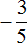
Согласно правилу, из двух отрицательных чисел больше то число, модуль которого меньше. Значит рациональное больше, чем , потому что модуль числа меньше, чем модуль числа

Сравнивать десятичные дроби намного проще, чем обыкновенные дроби и смешанные числа. В некоторых случаях, посмотрев на целую часть такой дроби, можно сразу ответить на вопрос какая дробь больше, а какая меньше.

Чтобы сделать это, нужно сравнить модули целых частей. Это позволит быстро ответить на вопрос в задаче. Ведь как известно, целые части в десятичных дробях имеют вес больший, чем дробные.

Пример 9. Сравнить рациональные числа 15,4 и 2,1256

Модуль целой части дроби 15,4 больше, чем модуль целой части дроби 2,1256

поэтому и дробь 15,4 больше, чем дробь 2,1256

Другими словами, нам не пришлось тратить время на дописывание нулей дроби 15,4 и сравнивать получившиеся дроби, как обычные числа

Правила сравнения остаются всё теми же. В нашем случае мы сравнивали положительные числа.

Пример 10. Сравнить рациональные числа −15,2 и −0,152

Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то число, модуль которого меньше. Но мы сравним только модули целых частей

Видим, что модуль целой части дроби −15,2 больше, чем модуль целой части дроби −0,152.

А значит рациональное −0,152 больше, чем −15,2 потому что модуль целой части числа −0,152 меньше, чем модуль целой части числа −15,2

Пример 11. Сравнить рациональные числа −3,4 и −3,7

Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то число, модуль которого меньше. Но мы сравним только модули целых частей. Но проблема в том, что модули целых чисел равны:

В этом случае придётся пользоваться старым методом: найти модули рациональных чисел и сравнить эти модули

Сравниваем найденные модули:

Согласно правилу, из двух отрицательных чисел больше то число, модуль которого меньше. Значит рациональное −3,4 больше, чем −3,7 потому что модуль числа −3,4 меньше, чем модуль числа −3,7

Пример 12. Сравнить рациональные числа 0,(3) и

Требуется сравнить два положительных числа. Причем сравнить периодическую дробь с простой дробью.

Переведём периодическую дробь 0,(3) в обыкновенную дробь и сравним её с дробью . После перевода периодической дроби 0,(3) в обыкновенную, она обращается в дробь

Находим модули чисел:

Сравниваем найденные модули. Но сначала приведём их к понятному виду, чтобы проще было сравнить, а именно приведём к общему знаменателю:

Согласно правилу, из двух положительных чисел больше то число, модуль которого больше. Значит рациональное число больше, чем 0,(3) потому что модуль числа больше, чем модуль числа 0,(3)

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Источник