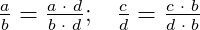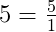Способы сравнения обыкновенных дробей 6 класс

Сравнение обыкновенных дробей

Сравнить две дроби — значит определить, какая из дробей больше, какая меньше или установить, что дроби равны.

Сравнение дробей с одинаковыми знаменателями

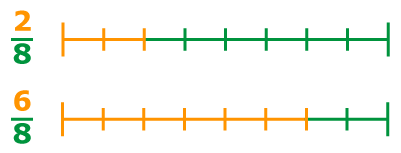
Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.

Пример. Дробь 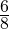больше чем дробь , потому что доли в обеих дробях одинаковы, но в первой дроби их больше, чем во второй.

Если изобразим единицу отрезком и разделим его на 8 долей, то легко увидеть, что дробь 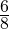больше :

Сравнение дробей с одинаковыми числителями

Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше.

Пример. Дробь 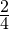больше чем дробь , потому что число долей в обеих дробях одинаково, но в первой дроби доли крупнее, чем во второй.

Изобразим две единицы в виде кругов, один разделим на 4 доли, второй на 6 долей. Теперь можно увидеть, что дробь 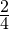больше :

Сравнение дробей с разными знаменателями и числителями

Чтобы сравнить дроби, у которых разные числители и знаменатели, нужно привести их к общему знаменателю. После этого их сравнивают по правилу сравнения дробей, у которых одинаковые знаменатели.

Пример. Сравните дроби: и .

Решение: приводим данные дроби к общему знаменателю:

Теперь сравниваем их по правилу сравнения дробей, у которых одинаковые знаменатели. Так как 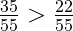, значит .

Приведём ещё один способ сравнения дробей с разными знаменателями и числителями. Рассмотрим сначала числовой пример.

Пример. Сравним дроби и .

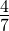
Решение: приводим данные дроби к общему знаменателю:

Решая данный пример можно заметить, что, после приведения дробей к общему знаменателю, задача сравнения свелась фактически к сравнению произведений

Так как 2 · 7 = 14, а 4 · 3 = 12, то

Значит, .

Теперь решим эту же задачу в общем виде, используя буквенную запись.

Пример. Пусть даны дроби и , где a и c — нуль или натуральные числа, b и d — натуральные числа. Приведём дроби к общему знаменателю:

1. если a · d >c · b, то
2. если a · d Пример.

Сравнение неправильной дроби с натуральным числом сводится к сравнению двух дробей.

Чтобы сравнить неправильную дробь с натуральным числом, нужно натуральное число представить в виде неправильной дроби со знаменателем 1, затем их можно сравнить одним из двух способов: используя перекрёстное правило, либо привести дроби к общему знаменателю. После этого их сравнивают по правилу сравнения дробей, у которых одинаковые знаменатели.

Пример. Сравните дробь с числом 5.

Решение: представим число 5 в виде дроби со знаменателем 1:

Приводим дроби к общему знаменателю:

Сравниваем числители, так как 11 Пример.

Онлайн калькулятор сравнения дробей

Данный калькулятор поможет вам сравнить обыкновенные дроби. Просто введите две дроби и нажмите кнопку Сравнить .

Источник

Урок математики в 6-м классе по теме «Сравнение дробей»

Разделы: Математика

Задачи занятия

Образовательные: научить учащихся сравнивать обыкновенные дроби различными способами

Развивающие: развивать логическое мышление, познавательные и аналитические способности, учить самостоятельно, добывать новые знания, способствовать развитию правильной математической речи

Воспитательные: формировать умение работать в коллективе, прислушиваться к мнению сверстников, взаимодействовать со взрослыми.

Этапы занятия	Временная реализация
Организационный момент: приветствие, объявление темы урока	3 минуты
Актуализация знаний	3 минуты
Создание различных проблемных ситуаций	15 минут
Промежуточное закрепление	10 минут
Самостоятельная работа	10 минут
Итог урока	4 минуты

1 этап (3 минуты)

Приветствие, объявление темы урока.

2 этап (3 минуты)

Как сравнить две обыкновенные дроби с одинаковыми знаменателями? Приведите пример.

Как сравнить две обыкновенные дроби с одинаковыми числителями? Приведите пример.

Как сравнить две обыкновенные дроби с разными знаменателями? Приведите пример.

С какими трудностями мы можем встретиться, сравнивая дроби с разными знаменателями?

Ученики — Иногда бывает трудно подобрать общий знаменатель, встречаются сложные вычисления.

Учитель — Оказывается ребята, наряду с уже хорошо известными нам способами сравнения обыкновенных дробей, существует несколько хитрых приемов, которые помогут нам сравнивать дроби проще и быстрее. Сейчас мы с вами и попробуем догадаться, что это за приемы.

3 этап (15 минут)

Учитель — Представьте частные в виде несократимых дробей:

Ученики — 1/2 2/3 3/4 4/5 5/6

Учитель — Что вы заметили?

Ученики — Числитель дроби на 1 меньше знаменателя.

Учитель — Как вы думаете, в каком порядке расположены дроби?

Ученики — В порядке увеличения.

Учитель — Как доказать?

Ученики — Можно привести к одному знаменателю.

Учитель — Отметьте эти точки на координатном луче, что вы заметили?

Ученики — Чем больше числитель и знаменатель, тем ближе расположено число к 1, т.е. 1/2 отличается от 1 на 1/2, 3/4 отличается от 1 на 1/4, 4/5 отличается от 1 на 1/5

1/2 > 1/3 >1/4 >1/5 > 1/6

Расстояния до 1 сокращаются, значит, сами числа увеличиваются!

Вывод: Обыкновенные дроби можно сравнивать, дополняя их до 1!

Учитель — Используя прием сравнения с 1, сравните:

Ученики —

Учитель — Как легче сравнить эти дроби? Приводя к одному знаменателю, или сравнивая с единицей?

Ученики — Конечно, сравнивая с единицей, так как иначе мы столкнемся со сложными вычислениями.

Учитель — Проанализируйте высказывание: если 3 · 7 14.05.2010

Источник

Сравнение дробей: правила, примеры, решения

Данная статья рассматривает сравнение дробей. Здесь мы выясним, какая из дробей больше или меньше, применим правило, разберем примеры решения. Сравним дроби как с одинаковыми, так и разными знаменателями. Произведем сравнение обыкновенной дроби с натуральным числом.

Сравнение дробей с одинаковыми знаменателями

Когда производится сравнение дробей с одинаковыми знаменателями, мы работаем только с числителем, а значит, сравниваем доли числа. Если имеется дробь 3 7 , то она имеет 3 доли 1 7 , тогда дробь 8 7 имеет 8 таких долей. Иначе говоря, если знаменатель одинаковый, производится сравнение числителей этих дробей, то есть 3 7 и 8 7 сравниваются числа 3 и 8 .

Отсюда следует правило сравнения дробей с одинаковыми знаменателями: из имеющихся дробей с одинаковыми показателями считается большей та дробь, у которой числитель больше и наоборот.

Это говорит о том, что следует обратить внимание на числители. Для этого рассмотрим пример.

Произвести сравнение заданных дробей 65 126 и 87 126 .

Так как знаменатели дробей одинаковые, переходим к числителям. Из чисел 87 и 65 очевидно, что 65 меньше. Исходя из правила сравнения дробей с одинаковыми знаменателями имеем, что 87 126 больше 65 126 .

Ответ: 87 126 > 65 126 .

Сравнение дробей с разными знаменателями

Сравнение таких дробей можно соотнести со сравнением дробей с одинаковыми показателями, но имеется различие. Теперь необходимо дроби приводить к общему знаменателю.

Если имеются дроби с разными знаменателями, для их сравнения необходимо:

• найти общий знаменатель;
• сравнить дроби.

Рассмотрим данные действия на примере.

Произвести сравнение дробей 5 12 и 9 16 .

В первую очередь необходимо привести дроби к общему знаменателю. Это делается таким образом: находится НОК, то есть наименьший общий делитель, 12 и 16 . Это число 48 . Необходимо надписать дополнительные множители к первой дроби 5 12 , это число находится из частного 48 : 12 = 4 , для второй дроби 9 16 – 48 : 16 = 3 . Запишем получившееся таким образом: 5 12 = 5 · 4 12 · 4 = 20 48 и 9 16 = 9 · 3 16 · 3 = 27 48 .

После сравнения дробей получаем, что 20 48 27 48 . Значит, 5 12 меньше 9 16 .

Ответ: 5 12 9 16 .

Имеется еще один способ сравнения дробей с разными знаменателями. Он выполняется без приведения к общему знаменателю. Рассмотрим на примере. Чтобы сравнить дроби a b и c d , приводим к общему знаменателю, тогда b · d , то есть произведение этих знаменателей. Тогда дополнительные множители для дробей будут являться знаменатели соседней дроби. Это запишется так a · d b · d и c · b d · b . Используя правило с одинаковыми знаменателями, имеем, что сравнение дробей свелось к сравнениям произведений a · d и c · b . Отсюда получаем правило сравнения дробей с разными знаменателями: если a · d > b · c , тогда a b > c d , но если a · d b · c , тогда a b c d . Рассмотрим сравнение с разными знаменателями.

Произвести сравнение дробей 5 18 и 23 86 .

Данный пример имеет a = 5 , b = 18 , c = 23 и d = 86 . Тогда необходимо вычислить a · d и b · c . Отсюда следует, что a · d = 5 · 86 = 430 и b · c = 18 · 23 = 414 . Но 430 > 414 , тогда заданная дробь 5 18 больше, чем 23 86 .

Ответ: 5 18 > 23 86 .

Сравнение дробей с одинаковыми числителями

Если дроби имеют одинаковые числители и разные знаменатели, тогда можно выполнять сравнение по предыдущему пункту. Результат сравнения возможет при сравнении их знаменателей.

Имеется правило сравнения дробей с одинаковыми числителями: из двух дробей с одинаковыми числителями больше та дробь, которая имеет меньший знаменатель и наоборот.

Рассмотрим на примере.

Произвести сравнение дробей 54 19 и 54 31 .

Решение

Имеем, что числители одинаковые, значит, что дробь, имеющая знаменатель 19 больше дроби, которая имеет знаменатель 31 . Это понятно, исходя из правила.

Ответ: 54 19 > 54 31 .

Иначе можно рассмотреть на примере. Имеется две тарелки, на которых 1 2 пирога, анна другой 1 16 . Если съесть 1 2 пирога, то насытишься быстрей, нежели только 1 16 . Отсюда вывод, что наибольший знаменатель при одинаковых числителях является наименьшим при сравнении дробей.

Сравнение дроби с натуральным числом

Сравнение обыкновенной дроби с натуральным числом идет как и сравнение двух дробей с записью знаменателей в виде 1 . Для детального рассмотрения ниже приведем пример.

Необходимо выполнить сравнение 63 8 и 9 .

Необходимо представить число 9 в виде дроби 9 1 . Тогда имеем необходимость сравнения дробей 63 8 и 9 1 . Далее следует приведение к общему знаменателю путем нахождения дополнительных множителей. После этого видим, что нужно сравнить дроби с одинаковыми знаменателями 63 8 и 72 8 . Исходя из правила сравнения, 63 72 , тогда получаем 63 8 72 8 . Значит, заданная дробь меньше целого числа 9 , то есть имеем 63 8 9 .

Источник