Способы создания когерентных источников

Способы получения когерентных источников света

Когерентные источники света – это источники, которые имеют постоянную во времени разность фаз, согласованное протекание нескольких колебательных или волновых процессов, степень которых различна.

Имеется много способов получения когерентных источников света, но суть их одинакова. С помощью разделения пучка на две части получают два мнимых источника света, дающих когерентные волны.

Интерференция света – сложение двух или нескольких световых волн с одинаковыми периодами, сходящихся в одной точке, в результате которого наблюдается увеличение или уменьшение амплитуда результирующей волны. Для получения устойчивой интерференционной картины необходимо, чтобы складываемые волны были когерентны. Когерентными называют волны с одинаковой частотой (периодом) и постоянной во времени разностью фаз. Чтобы получить когерентные волны необходимо световую волну от одного источника разделить на две или несколько волн. После прохождения различных путей эти волны, имея некоторую разность хода, интерферируют.

Приёмы разделения волны:

· С помощью бипризмы Френеля:

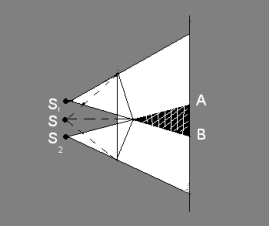
Волна, идущая от источника света, раздваивается из-за преломления света в двух половинах бипризмы. Получаемы волны 1 и 2 как бы исходят от двух мнимых источников S₁ и S₂ и являются когерентными, поэтому в заштрихованной области наблюдается интерференция.

Свет, проходящий через узкое отверстие S, падает на экран с двумя отверстиями S₁ и S₂ и делится на две когерентных волны, поэтому в заштрихованной области наблюдается интерференция, а на экране – интерференционная картина.

2. Вывод выражения для расстояния l между мнимыми изображения источника в случае бипризмы.

Бипризма Френеля представляет собой изготовленные из одного куска стекла две симметричные призмы, имеющие общее основание и малый преломляющий угол G≈1°. На расстоянии L₁ от бипризмы располагается источник света S. Можно показать, что в этом случае, если преломляющий угол призмы мал и лучи падают на призму под небольшими углами, все лучи отклоняются призмой почти на одинаковый угол ϕ, равный

где n – показатель преломления стекла, из которого изготовлена призма, α – преломляющий угол каждой половинки бипризмы. При этом мнимые изображения S₁ и S₂ точечного источника света S лежат с ним в одной плоскости. В результате образуются две когерентные волны, исходящие из мнимых источников S₁ и S₂. Расстояние d между мнимыми источниками равно:

где L₁ – расстояние между источником S и бипризмой. При этом, sin ϕ≈ϕ (так как угол ϕ достаточно мал), тогда:

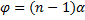
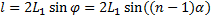
Источник

Способы создания когерентных источников

Когерентные источники получают, разделив световую волну, идущую от одного источника на две.

18.2.1. Опыт Юнга

Томас Юнг наблюдал интерференцию от двух источников, прокалывая на малом расстоянии (d ≈ 1мм) два маленьких отверстия в непрозрачном экране. Отверстия освещались светом от солнца, прошедшим через малое отверстие в другом непрозрачном экране. [an error occurred while processing this directive]

Интерференционная картина наблюдалась на экране, удаленном на расстоянии L ≈ 1м от двух источников. Так, впервые в истории, Т. Юнг определил длины световых волн.

При использовании лазера в качестве источника света необходимость в экране отпадает.

18.2.2. Зеркала Френеля

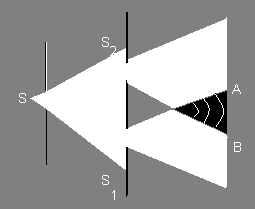
Свет от узкой щели S падает на два плоских зеркала, развернутых друг относительно друга на очень малый угол φ . Используя закон отражения света (17.1.3.) нетрудно показать, что падающий пучок света разобьется на два, исходящих из мнимых источников S₁ и S₂ . Источник S закрывают от экрана наблюдения непрозрачным экраном.

18.2.3. Бипризма Френеля

Две стеклянные призмы с малым преломляющим углом θ изготавливают из одного куска стекла так, что призмы сложены своими основаниями, Источник света — ярко освещенная щель S . После преломления в бипризме падающий пучок расщепляется на два, исходящих от мнимых источников S₁ и S₂ , которые дают две когерентные цилиндрические волны.

Так как преломляющий угол θ мал, то все лучи отклоняются каждой из половинок бипризмы на один и тот же угол φ . Можно показать, что в этом случае

,

здесь n — показатель преломления материала призмы.

Расстояние между источниками:

.

18.2.4. Интерференция при отражении от прозрачных пластинок

Луч света, падающий на прозрачную пластинку, частично отражается и частично преломляется. Преломленный луч, отражаясь от нижней поверхности пластинки, идет к верхней и преломляется на ней второй раз. Таким образом получаются два луча.

Если источник света естественный, то необходимым условием когерентности является малая толщина пластинок (интерференция в тонких пленках). При освещении лазерным лучом это ограничение отпадает.

При определении оптической разности хода необходимо учитывать изменение фазы отраженной волны на противоположную, если отражение происходит от оптически более плотной среды.

.

.

Здесь λ₀/2 появилась за счет изменения фазы волны на противоположную при отражении в точке A . Связь разности фаз δ и разности хода Δ , см. (18.1.2.2.).

18.2.4.1. Кольца Ньютона

Плосковыпуклая линза большого радиуса кладется на стеклянную пластинку и освещается сверху параллельным пучком света. Так как радиус линзы R велик по сравнению с r — радиусом интерференционных полос, то угол падения света на внутреннюю поверхность линзы i ≈ 0 . Тогда геометрическая разность хода с большой точностью равна 2b . При нахождении оптической разности хода следует учитывать изменение фазы на противоположную при отражении от оптически более плотной среды. Связь между b, r и R нетрудно найти из геометрических соображений.

Если в зазоре между линзой и пластиной n = 1 , то для радиуса интерференционных полос (колец Ньютона) получается формула:

При четном m кольца Ньютона темные, в частности при m = 0, r = 0 и в центре наблюдается темное пятно (из-за потери λ₀/2 при отражении от стеклянной пластинки).

Если m нечетное, то кольца светлые.

18.3. Многолучевая интерференция

Пусть в заданную точку экрана посылают световые волны N источников одинаковой интенсивности ( N > 2 ).

Предположим, что колебание, возбуждаемое каждым последующим источником сдвинуто по фазе относительно предыдущего на δ . Результирующую амплитуду A можно выразить через A₀ — амплитуду от одного источника, используя метод векторной диаграммы (14.3.1, 14.3.2).

Выразим A и A₀ через вспомогательный параметр R — радиус окружности, на которой лежат начала и концы наших векторов:

После исключения R получим амплитуду результирующего колебания:

.

Если δ = 0 (все колебания имеют одинаковую фазу) полученное выражение становится неопределенным. Взяв производную по δ от числителя и знаменателя, найдем по правилу Лопиталя, что при δ = 0 амплитуда результирующего колебания:

.

Этот результат непосредственно очевиден из векторной диаграммы, построенной для случая δ = 0 , т.к. все векторы будут направлены вдоль одной прямой. Интенсивность света (16.5.4) I

.

.

Источник

Способы получения когерентных источников

Работа № 2. ИНТЕРФЕРЕНЦИЯ СВЕТА

Цель работы: получение интерференционной картины разными способами, определение длины волны по интерференционной картине.

Вопросы, знание которых обязательно

для допуска к выполнению работы:

1. В чем заключается явление интерференции?

2. Какие источники называются когерентными?

3. Способы получения когерентных источников, методом деления волнового фронта.

4. Способы получения когерентных источников, методом деления амплитуд.

5. Условия наблюдения интерференционной картины.

6. Оптическая разность хода

7. Условия максимума и минимума интерференционной картины

ВВЕДЕНИЕ

При наложении световых волн происходит перераспределение светового потока в пространстве, в результате чего наблюдается явление интерференции, заключающееся в том, что в одних местах происходит усиление света, в других – ослабление. Если две световые волны придут в одну точку пространства в одинаковой фазе, они будут усиливать друг друга. В этой точке образуется светлый участок интерференционной картины. В тех же точках пространства, в которые волны приходят в противоположных фазах, они будут ослаблять друг друга и там будет темный участок.

Таким образом, результат интерференции зависит от разности фаз интерферирующих волн. Чтобы картина интерференции в каждой точке пространства не менялась со временем, необходимо, чтобы разность фаз была постоянной. В противном случае в каждой точке пространства волны будут то усиливать, то ослаблять друг друга, а глаз, воспринимая усредненную картину, не обнаружит интерференционных полос. Следовательно, наблюдать интерференционную картину можно лишь в том случае, если интерферирующие волны имеют строго одинаковую частоту и постоянную разность фаз в пространстве и во времени.

Источники света, излучающие волны одинаковой частоты и с постоянной разностью фаз, называются когерентными.Для образования картины интерференции необходимо, чтобы пучки электромагнитных волн при своем движении набрали разность хода. Рассмотрим интерференцию света от двух точечных когерентных источников S₁ и S₂, расстояние между которыми равно d (рис.1).

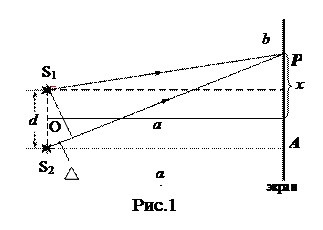
Проведем перпендикулярно отрезку S₁ S₂ через его середину прямую OA. Возьмем точку P на прямой параллельной S₁ S₂, и обозначим OA через а, а АР – через х.

Тогда по теореме Пифагора:

, (1)

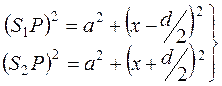
где и – пути, которые пройдут лучи света от источников S₁ и S₂ до точки P, в которой наблюдается интерференция. Из уравнений (1) следует, что оптическая разность хода между двумя лучами

. (2)

, (3)

Если х и d малы по сравнению с а, то приближенно и

. (4)

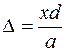
Если величина D равна нечетному числу полуволн, то световые волны придут в точку P в противофазе и погасят друг друга, интенсивность в этой точке будет минимальной: , где; k = 0,1,2…; λ – длина волны.

Если же равна четному числу полуволн, то световые волны придут в точку P в одинаковых фазах и усилят друг друга – интенсивность будет максимальной: , где ; λ – длина волны.

Таким образом, в точках будут светлые участки интерференционной картины, а в точках – темные участки интерференционной картины. В результате в плоскости РА будут наблюдаться светлые и темные полосы. Расстояние bмежду центрами соседних k-й и (k + 1)-й светлых полос составит:

. (5)

Такое же расстояние будет и между центрами темных полос.

Способы получения когерентных источников

Найти два точечных когерентных источника практически невозможно. Значительно проще поделить волновой фронт или амплитуду излученной волны. Наиболее распространенными методами получения когерентных источников являются: опыт Юнга, бипризма Френеля, билинза Бийе, «кольца» Ньютона, опыт Поля (с помощью плоскопараллельной пластины).

1. Бипризма Френеля (рис.2) состоит из двух остроугольных призм (с малыми преломляющими углами), сложенных основаниями. Обычно обе призмы имеют очень малые преломляющие углы B и C. В сечении бипризма Френеля представляет собой два равнобедренных треугольника с углом A, близким к 180º, тогда угол при вершине очень мал.

Свет от монохроматического источника S (например, от узкой освещенной щели, перпендикулярной плоскости чертежа) падает на бипризму и преломляется в ней. Угол падения лучей на бипризму мал, вследствие чего все лучи отклоняются бипризмой на одинаковый угол. В результате образуются две когерентные волны, исходящие из мнимых источников S₁и S₂. В заштрихованной области за бипризмой преломленные пучки интерферируют, в результате чего образуется интерференционная картина, состоящая из светлых и темных полос.

2. Воздушный клин (кольца Ньютона). «Кольца Ньютона» представляют собой один из видов интерференции в тонкой пленке, а именно, полосы равной толщины в виде окружностей. Они получаются при наложении линзы радиуса R выпуклой поверхностью на отражающую стеклянную поверхность меньшей кривизны (например, плоскую). Вблизи места соприкосновения получается слой воздуха, толщина которого сравнима с длиной световой волны. Интерференция возникает в результате наложения лучей 1 и 2, после отражения от пластины и линзы (1¢ и 2¢) (рис.4). Полная разность хода между «усиливающими» друг друга лучами 1 и 2 определяется как ∆ » 2d∙λ/2 (величина разности хода увеличена на λ /2вследствие потери полуволны лучом 2 при отражении от оптически более плотной поверхности на границе раздела воздух – стекло). Толщина воздушного зазора d зависит (рис.4) от расстояния r до точки соприкосновения линзы с пластинкой. Из треугольника АОС (рис. 4) имеем при R >> d. Для точек, в которых выполняется условие , будет наблюдаться максимум интенсивности. Отсюда радиус k—того светлого кольца . Аналогично радиус темного кольца .

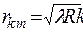
На практике кольца Ньютона наблюдают либо невооруженным глазом, помещая его на пути лучей 1 и 2 (рис.4), либо в фокальной плоскости окуляра микроскопа при использовании микроскопа. В отраженном свете в центре интерференционной картины наблюдается темное пятно, которое объясняется тем, что геометрическая разность хода между лучами 1 и 2 в области точки С равна нулю, а полуволна теряется при отражении от оптически более плотной поверхности на границе воздух – стекло.

Измеряя радиусы колец и зная длину волны λ, можно было бы найти по вышеприведенным формулам радиус кривизны линзы и обратно – по известному радиусу кривизны найти длину волны. Однако эти формулы неприменимы для опытной проверки. На поверхности даже очищенного стекла всегда присутствуют пылинки, и линза не примыкает плотно к плоскопараллельной пластинке, между ними имеется незначительный зазор величиной h. Вследствие зазора возникает дополнительная разность хода в 2h. Тогда условие образования темных колец примет вид или , а радиус k-того темного кольца . На опыте измеряют радиусы темных колец r_k и строят зависимость r 2 _kт(k), где k = 2, 3. . и использую следующее соотношение

, (13)

при известной величинеλнаходят R (или, наоборот, при известном R определяется λ).

В случае, если рассматриваем «кольца» Ньютона в проходящем свете, тогда не будет дополнительной разности хода в 2h и, следовательно, там где в отраженном свете наблюдались темные кольца в походящем будут белыми и наоборот.

Источник