12. Методы сортировки массивов

Сортировкой или упорядочением массива называется расположение его элементов по возрастанию (или убыванию). Если не все элементы различны, то надо говорить о неубывающем (или невозрастающем) порядке.

• количество шагов алгоритма, необходимых для упорядочения;
• количество сравнений элементов;
• количество перестановок, выполняемых при сортировке.

Мы рассмотрим только три простейшие схемы сортировки.

Метод «пузырька»

По-видимому, самым простым методом сортировки является так называемый метод » пузырька «. Чтобы уяснить его идею, представьте , что массив (таблица) расположен вертикально. Элементы с большим значением всплывают вверх наподобие больших пузырьков. При первом проходе вдоль массива, начиная проход «снизу», берется первый элемент и поочередно сравнивается с последующими. При этом:

В результате наибольший элемент оказывается в самом верху массива.

Во время второго прохода вдоль массива находится второй по величине элемент, который помещается под элементом, найденным при первом проходе, т.е на вторую сверху позицию, и т.д.

Заметим, что при втором и последующих проходах, нет необходимости рассматривать ранее «всплывшие» элементы, т.к. они заведомо больше оставшихся. Другими словами, во время j -го прохода не проверяются элементы, стоящие на позициях выше j .

Теперь можно привести текст программы упорядочения массива M[1..N] :

begin for j :=1 to N -1 do for i :=1 to N — j do if M[ i ] > M[ i +1] then swap (M[ i ],M[ i +1]) end;

Стандартная процедура swap будет использоваться и в остальных алгоритмах сортировки для перестановки элементов (их тип мы уточнять не будем) местами:

procedure swap (var x,y: . );
var t: . ;
begin
t := x;
x := y;
y := t
end;

Заметим, что если массив M — глобальный, то процедура могла бы содержать только аргументы (а не результаты). Кроме того, учитывая специфику ее применения в данном алгоритме, можно свести число парметров к одному (какому?), а не двум.

Применение метода «пузырька» можно проследить здесь.

Сортировка вставками

Второй метод называется метод вставок ., т.к. на j -ом этапе мы «вставляем» j -ый элемент M[j] в нужную позицию среди элементов M[1] , M[2] ,. . ., M[j-1] , которые уже упорядочены. После этой вставки первые j элементов массива M будут упорядочены.
Сказанное можно записать следующим образом:

Чтобы сделать процесс перемещения элемента M[j] , более простым, полезно воспользоваться барьером: ввести «фиктивный» элемент M[0] , чье значение будет заведомо меньше значения любого из «реальных»элементов массива (как это можно сделать?). Мы обозначим это значение через —оо.

Если барьер не использовать, то перед вставкой M[j] , в позицию i-1 надо проверить, не будет ли i=1 . Если нет, тогда сравнить M[j] ( который в этот момент будет находиться в позиции i ) с элементом M[i-1].

Описанный алгоритм имеет следующий вид:

begin M[0] := -oo; for j :=2 to N do begin i := j ; while M[ i ] M[ i — 1] do begin swap (M[ i ],M[ i -1]); i := i -1 end end end;

Процедура swap нам уже встречалась.

Сортировка посредством выбора

Идея сортировки с помощью выбора не сложнее двух предыдущих. На j -ом этапе выбирается элемент наименьший среди M[j] , M[j+1] ,. . ., M[N] (см. процедуру FindMin ) и меняется местами с элементом M[j] . В результате после j -го этапа все элементы M[j] , M[j+1] ,. . ., M[N] будут упорядочены.

Сказанное можно описать следующим образом:

нц для j от 1 до N-1
выбрать среди M[j] ,. . ., M[N] наименьший элемент и
поменять его местами с M[j]
кц

begin for j :=1 to N -1 do begin FindMin ( j , i ); swap (M[ j ],M[ i ]) end end;

В программе, как уже было сказано, используется процедура FindMin , вычисляющая индекс lowindex элемента, наименьшего среди элементов массива с индексами не меньше, чем startindex :

procedure FindMin (start index : integer; var lowindex : integer );
var lowelem: . ;
u: integer;
begin
lowindex := start index ;
lowelem := M[startindex];
for u:= start index +1 to N do
if M[u] lowelem then
begin
lowelem := M[u];
lowindex := u
end
end;

Оценивая эффективность применения , учтите что в демонстрации сортировки выбором отсутствует пошаговое выполнение этой процедуры.

Источник

Pascal. Сортировка одномерных массивов.

В практике программиста часто случается так, что нужно разместить какие-либо данные в определенном порядке. В Паскале для таких случаев предусмотрена сортировка. Существует два основных алгоритма сортировки. Первый из них — метод прямого выбора. Ее смысл заключается в том, что за счет вложенности циклов каждый элемент массива сравнивается с остальными.

То есть, если у нас 10 чисел, то сначала первое из них будет сравниваться до тех пор, пока не будет найдено другой, например, большее его (если мы сортируем просто по возрастанию). Далее так же будет сравниваться 2, 3, 4 … элементы с последующими, но не с теми, которые уже отсортированы.

Прелесть этого вида сортировки заключается в том, что она очень проста для начинающего программиста, и все обычно начинают именно с неё. Давайте же рассмотрим пример. Пусть нам дан массив из 20 элементом и нам нужно отсортировать по убыванию.

Обратите внимание на 2 первые строки после Begin. Здесь мы вызываем процедуру генерации случайных чисел. То есть просто заполняем наш массив числами от 1 до 100. Далее в цикле выводится для пользователя первоначальный массив.

Далее следует сам алгоритм сортировки, для новичков объясним, что это 2 цикла for , первый из них, в данной случае, идет с самого начала и до N-1 (1 первого до предпоследнего элемента).

Далее вложенный for , где используется уже другой счетчик j . Он изменяется от текущего i -того, увеличенного на 1 и до конца. И далее мы проверяем 2 элемента массива в условии и, если все нас устраивает, то производим обмен переменными. В последнем цикле мы выводим отсортированный массив.

Заметим, что первоначальный массив при сортировке не сохраняется. Кроме того хочу вам показать, как можно сделать так, чтобы первая половина массива была отсортирована по возрастанию, а вторая — по убыванию.

Источник

Основные виды сортировок и примеры их реализации

Памятка для тех, кто готовится к собеседованию на позицию разработчика

На собеседованиях будущим стажёрам-разработчикам дают задания на знание структур данных и алгоритмов — в том числе сортировок. Академия Яндекса и соавтор специализации «Искусство разработки на современном C++» Илья Шишков составили список для подготовки с методами сортировки, примерами их реализации и гифками, чтобы лучше понять, как они работают.

Пузырьковая сортировка и её улучшения

Сортировка пузырьком

Сортировка пузырьком — один из самых известных алгоритмов сортировки. Здесь нужно последовательно сравнивать значения соседних элементов и менять числа местами, если предыдущее оказывается больше последующего. Таким образом элементы с большими значениями оказываются в конце списка, а с меньшими остаются в начале.

Этот алгоритм считается учебным и почти не применяется на практике из-за низкой эффективности: он медленно работает на тестах, в которых маленькие элементы (их называют «черепахами») стоят в конце массива. Однако на нём основаны многие другие методы, например, шейкерная сортировка и сортировка расчёской.

Сортировка перемешиванием (шейкерная сортировка)

Шейкерная сортировка отличается от пузырьковой тем, что она двунаправленная: алгоритм перемещается не строго слева направо, а сначала слева направо, затем справа налево.

Сортировка расчёской

Сортировка расчёской — улучшение сортировки пузырьком. Её идея состоит в том, чтобы «устранить» элементы с небольшими значения в конце массива, которые замедляют работу алгоритма. Если при пузырьковой и шейкерной сортировках при переборе массива сравниваются соседние элементы, то при «расчёсывании» сначала берётся достаточно большое расстояние между сравниваемыми значениями, а потом оно сужается вплоть до минимального.

Первоначальный разрыв нужно выбирать не случайным образом, а с учётом специальной величины — фактора уменьшения, оптимальное значение которого равно 1,247. Сначала расстояние между элементами будет равняться размеру массива, поделённому на 1,247; на каждом последующем шаге расстояние будет снова делиться на фактор уменьшения — и так до окончания работы алгоритма.

Простые сортировки

Сортировка вставками

При сортировке вставками массив постепенно перебирается слева направо. При этом каждый последующий элемент размещается так, чтобы он оказался между ближайшими элементами с минимальным и максимальным значением.

Сортировка выбором

Сначала нужно рассмотреть подмножество массива и найти в нём максимум (или минимум). Затем выбранное значение меняют местами со значением первого неотсортированного элемента. Этот шаг нужно повторять до тех пор, пока в массиве не закончатся неотсортированные подмассивы.

Быстрая сортировка

Этот алгоритм состоит из трёх шагов. Сначала из массива нужно выбрать один элемент — его обычно называют опорным. Затем другие элементы в массиве перераспределяют так, чтобы элементы меньше опорного оказались до него, а большие или равные — после. А дальше рекурсивно применяют первые два шага к подмассивам справа и слева от опорного значения.

Быструю сортировку изобрели в 1960 году для машинного перевода: тогда словари хранились на магнитных лентах, а сортировка слов обрабатываемого текста позволяла получить переводы за один прогон ленты, без перемотки назад.

Сортировка слиянием

Сортировка слиянием пригодится для таких структур данных, в которых доступ к элементам осуществляется последовательно (например, для потоков). Здесь массив разбивается на две примерно равные части и каждая из них сортируется по отдельности. Затем два отсортированных подмассива сливаются в один.

Пирамидальная сортировка

При этой сортировке сначала строится пирамида из элементов исходного массива. Пирамида (или двоичная куча) — это способ представления элементов, при котором от каждого узла может отходить не больше двух ответвлений. А значение в родительском узле должно быть больше значений в его двух дочерних узлах.

Пирамидальная сортировка похожа на сортировку выбором, где мы сначала ищем максимальный элемент, а затем помещаем его в конец. Дальше нужно рекурсивно повторять ту же операцию для оставшихся элементов.

Источник

Описание алгоритмов сортировки и сравнение их производительности

Вступление

На эту тему написано уже немало статей. Однако я еще не видел статьи, в которой сравниваются все основные сортировки на большом числе тестов разного типа и размера. Кроме того, далеко не везде выложены реализации и описание набора тестов. Это приводит к тому, что могут возникнуть сомнения в правильности исследования. Однако цель моей работы состоит не только в том, чтобы определить, какие сортировки работают быстрее всего (в целом это и так известно). В первую очередь мне было интересно исследовать алгоритмы, оптимизировать их, чтобы они работали как можно быстрее. Работая над этим, мне удалось придумать эффективную формулу для сортировки Шелла.

Во многом статья посвящена тому, как написать все алгоритмы и протестировать их. Если говорить о самом программировании, то иногда могут возникнуть совершенно неожиданные трудности (во многом благодаря оптимизатору C++). Однако не менее трудно решить, какие именно тесты и в каких количествах нужно сделать. Коды всех алгоритмов, которые выложены в данной статье, написаны мной. Доступны и результаты запусков на всех тестах. Единственное, что я не могу показать — это сами тесты, поскольку они весят почти 140 ГБ. При малейшем подозрении я проверял и код, соответствующий тесту, и сам тест. Надеюсь, что статья Вам понравится.

Описание основных сортировок и их реализация

Я постараюсь кратко и понятно описать сортировки и указать асимптотику, хотя последнее в рамках данной статьи не очень важно (интересно же узнать реальное время работы). О потреблении памяти в дальнейшем ничего писать не буду, замечу только, что сортировки, использующие непростые структуры данных (как, например, сортировка деревом), обычно потребляют ее в больших количествах, а остальные сортировки в худшем случае только создают вспомогательный массив. Также существует понятие стабильности (устойчивости) сортировки. Это значит, что относительный порядок элементов при их равенстве не меняется. Это тоже в рамках данной статьи неважно (в конце концов, можно просто прицепить к элементу его индекс), однако в одном месте пригодится.

Сортировка пузырьком / Bubble sort

Будем идти по массиву слева направо. Если текущий элемент больше следующего, меняем их местами. Делаем так, пока массив не будет отсортирован. Заметим, что после первой итерации самый большой элемент будет находиться в конце массива, на правильном месте. После двух итераций на правильном месте будут стоять два наибольших элемента, и так далее. Очевидно, не более чем после n итераций массив будет отсортирован. Таким образом, асимптотика в худшем и среднем случае – O(n 2 ), в лучшем случае – O(n).

Шейкерная сортировка / Shaker sort

(также известна как сортировка перемешиванием и коктейльная сортировка). Заметим, что сортировка пузырьком работает медленно на тестах, в которых маленькие элементы стоят в конце (их еще называют «черепахами»). Такой элемент на каждом шаге алгоритма будет сдвигаться всего на одну позицию влево. Поэтому будем идти не только слева направо, но и справа налево. Будем поддерживать два указателя begin и end, обозначающих, какой отрезок массива еще не отсортирован. На очередной итерации при достижении end вычитаем из него единицу и движемся справа налево, аналогично, при достижении begin прибавляем единицу и двигаемся слева направо. Асимптотика у алгоритма такая же, как и у сортировки пузырьком, однако реальное время работы лучше.

Сортировка расческой / Comb sort

Еще одна модификация сортировки пузырьком. Для того, чтобы избавиться от «черепах», будем переставлять элементы, стоящие на расстоянии. Зафиксируем его и будем идти слева направо, сравнивая элементы, стоящие на этом расстоянии, переставляя их, если необходимо. Очевидно, это позволит «черепахам» быстро добраться в начало массива. Оптимально изначально взять расстояние равным длине массива, а далее делить его на некоторый коэффициент, равный примерно 1.247. Когда расстояние станет равно единице, выполняется сортировка пузырьком. В лучшем случае асимптотика равна O(nlogn), в худшем – O(n 2 ). Какая асимптотика в среднем мне не очень понятно, на практике похоже на O(nlogn).

Об этих сортировках (пузырьком, шейкерной и расческой) также можно почитать здесь.

Сортировка вставками / Insertion sort

Создадим массив, в котором после завершения алгоритма будет лежать ответ. Будем поочередно вставлять элементы из исходного массива так, чтобы элементы в массиве-ответе всегда были отсортированы. Асимптотика в среднем и худшем случае – O(n 2 ), в лучшем – O(n). Реализовывать алгоритм удобнее по-другому (создавать новый массив и реально что-то вставлять в него относительно сложно): просто сделаем так, чтобы отсортирован был некоторый префикс исходного массива, вместо вставки будем менять текущий элемент с предыдущим, пока они стоят в неправильном порядке.

Сортировка Шелла / Shellsort

Используем ту же идею, что и сортировка с расческой, и применим к сортировке вставками. Зафиксируем некоторое расстояние. Тогда элементы массива разобьются на классы – в один класс попадают элементы, расстояние между которыми кратно зафиксированному расстоянию. Отсортируем сортировкой вставками каждый класс. В отличие от сортировки расческой, неизвестен оптимальный набор расстояний. Существует довольно много последовательностей с разными оценками. Последовательность Шелла – первый элемент равен длине массива, каждый следующий вдвое меньше предыдущего. Асимптотика в худшем случае – O(n 2 ). Последовательность Хиббарда – 2 n — 1, асимптотика в худшем случае – O(n 1,5 ), последовательность Седжвика (формула нетривиальна, можете ее посмотреть по ссылке ниже) — O(n 4/3 ), Пратта (все произведения степеней двойки и тройки) — O(nlog 2 n). Отмечу, что все эти последовательности нужно рассчитать только до размера массива и запускать от большего от меньшему (иначе получится просто сортировка вставками). Также я провел дополнительное исследование и протестировал разные последовательности вида s_i = a * s_{i — 1} + k * s_{i — 1} (отчасти это было навеяно эмпирической последовательностью Циура – одной из лучших последовательностей расстояний для небольшого количества элементов). Наилучшими оказались последовательности с коэффициентами a = 3, k = 1/3; a = 4, k = 1/4 и a = 4, k = -1/5.

Несколько полезных ссылок:

Сортировка деревом / Tree sort

Будем вставлять элементы в двоичное дерево поиска. После того, как все элементы вставлены достаточно обойти дерево в глубину и получить отсортированный массив. Если использовать сбалансированное дерево, например красно-черное, асимптотика будет равна O(nlogn) в худшем, среднем и лучшем случае. В реализации использован контейнер multiset.

Здесь можно почитать про деревья поиска:

Гномья сортировка / Gnome sort

Алгоритм похож на сортировку вставками. Поддерживаем указатель на текущий элемент, если он больше предыдущего или он первый — смещаем указатель на позицию вправо, иначе меняем текущий и предыдущий элементы местами и смещаемся влево.

Сортировка выбором / Selection sort

На очередной итерации будем находить минимум в массиве после текущего элемента и менять его с ним, если надо. Таким образом, после i-ой итерации первые i элементов будут стоять на своих местах. Асимптотика: O(n 2 ) в лучшем, среднем и худшем случае. Нужно отметить, что эту сортировку можно реализовать двумя способами – сохраняя минимум и его индекс или просто переставляя текущий элемент с рассматриваемым, если они стоят в неправильном порядке. Первый способ оказался немного быстрее, поэтому он и реализован.

Пирамидальная сортировка / Heapsort

Развитие идеи сортировки выбором. Воспользуемся структурой данных «куча» (или «пирамида», откуда и название алгоритма). Она позволяет получать минимум за O(1), добавляя элементы и извлекая минимум за O(logn). Таким образом, асимптотика O(nlogn) в худшем, среднем и лучшем случае. Реализовывал кучу я сам, хотя в С++ и есть контейнер priority_queue, поскольку этот контейнер довольно медленный.

Почитать про кучу можно здесь:

Быстрая сортировка / Quicksort

Выберем некоторый опорный элемент. После этого перекинем все элементы, меньшие его, налево, а большие – направо. Рекурсивно вызовемся от каждой из частей. В итоге получим отсортированный массив, так как каждый элемент меньше опорного стоял раньше каждого большего опорного. Асимптотика: O(nlogn) в среднем и лучшем случае, O(n 2 ). Наихудшая оценка достигается при неудачном выборе опорного элемента. Моя реализация этого алгоритма совершенно стандартна, идем одновременно слева и справа, находим пару элементов, таких, что левый элемент больше опорного, а правый меньше, и меняем их местами. Помимо чистой быстрой сортировки, участвовала в сравнении и сортировка, переходящая при малом количестве элементов на сортировку вставками. Константа подобрана тестированием, а сортировка вставками — наилучшая сортировка, подходящая для этой задачи (хотя не стоит из-за этого думать, что она самая быстрая из квадратичных).

Сортировка слиянием / Merge sort

Сортировка, основанная на парадигме «разделяй и властвуй». Разделим массив пополам, рекурсивно отсортируем части, после чего выполним процедуру слияния: поддерживаем два указателя, один на текущий элемент первой части, второй – на текущий элемент второй части. Из этих двух элементов выбираем минимальный, вставляем в ответ и сдвигаем указатель, соответствующий минимуму. Слияние работает за O(n), уровней всего logn, поэтому асимптотика O(nlogn). Эффективно заранее создать временный массив и передать его в качестве аргумента функции. Эта сортировка рекурсивна, как и быстрая, а потому возможен переход на квадратичную при небольшом числе элементов.

Сортировка подсчетом / Counting sort

Создадим массив размера r – l, где l – минимальный, а r – максимальный элемент массива. После этого пройдем по массиву и подсчитаем количество вхождений каждого элемента. Теперь можно пройти по массиву значений и выписать каждое число столько раз, сколько нужно. Асимптотика – O(n + r — l). Можно модифицировать этот алгоритм, чтобы он стал стабильным: для этого определим место, где должно стоять очередное число (это просто префиксные суммы в массиве значений) и будем идти по исходному массиву слева направо, ставя элемент на правильное место и увеличивая позицию на 1. Эта сортировка не тестировалась, поскольку большинство тестов содержало достаточно большие числа, не позволяющие создать массив требуемого размера. Однако она, тем не менее, пригодилась.

Блочная сортировка / Bucket sort

(также известна как корзинная и карманная сортировка). Пусть l – минимальный, а r – максимальный элемент массива. Разобьем элементы на блоки, в первом будут элементы от l до l + k, во втором – от l + k до l + 2k и т.д., где k = (r – l) / количество блоков. В общем-то, если количество блоков равно двум, то данный алгоритм превращается в разновидность быстрой сортировки. Асимптотика этого алгоритма неясна, время работы зависит и от входных данных, и от количества блоков. Утверждается, что на удачных данных время работы линейно. Реализация этого алгоритма оказалась одной из самых трудных задач. Можно сделать это так: просто создавать новые массивы, рекурсивно их сортировать и склеивать. Однако такой подход все же довольно медленный и меня не устроил. В эффективной реализации используется несколько идей:

1) Не будем создавать новых массивов. Для этого воспользуемся техникой сортировки подсчетом – подсчитаем количество элементов в каждом блоке, префиксные суммы и, таким образом, позицию каждого элемента в массиве.

2) Не будем запускаться из пустых блоков. Занесем индексы непустых блоков в отдельный массив и запустимся только от них.

3) Проверим, отсортирован ли массив. Это не ухудшит время работы, так как все равно нужно сделать проход с целью нахождения минимума и максимума, однако позволит алгоритму ускориться на частично отсортированных данных, ведь элементы вставляются в новые блоки в том же порядке, что и в исходном массиве.

4) Поскольку алгоритм получился довольно громоздким, при небольшом количестве элементов он крайне неэффективен. До такой степени, что переход на сортировку вставками ускоряет работу примерно в 10 раз.

Осталось только понять, какое количество блоков нужно выбрать. На рандомизированных тестах мне удалось получить следующую оценку: 1500 блоков для 10 7 элементов и 3000 для 10 8 . Подобрать формулу не удалось – время работы ухудшалось в несколько раз.

Поразрядная сортировка / Radix sort

(также известна как цифровая сортировка). Существует две версии этой сортировки, в которых, на мой взгляд, мало общего, кроме идеи воспользоваться представлением числа в какой-либо системе счисления (например, двоичной).

LSD (least significant digit):

Представим каждое число в двоичном виде. На каждом шаге алгоритма будем сортировать числа таким образом, чтобы они были отсортированы по первым k * i битам, где k – некоторая константа. Из данного определения следует, что на каждом шаге достаточно стабильно сортировать элементы по новым k битам. Для этого идеально подходит сортировка подсчетом (необходимо 2 k памяти и времени, что немного при удачном выборе константы). Асимптотика: O(n), если считать, что числа фиксированного размера (а в противном случае нельзя было бы считать, что сравнение двух чисел выполняется за единицу времени). Реализация довольно проста.

MSD (most significant digit):

На самом деле, некоторая разновидность блочной сортировки. В один блок будут попадать числа с равными k битами. Асимптотика такая же, как и у LSD версии. Реализация очень похожа на блочную сортировку, но проще. В ней используется функция digit, определенная в реализации LSD версии.

Битонная сортировка / Bitonic sort:

Идея данного алгоритма заключается в том, что исходный массив преобразуется в битонную последовательность – последовательность, которая сначала возрастает, а потом убывает. Ее можно эффективно отсортировать следующим образом: разобьем массив на две части, создадим два массива, в первый добавим все элементы, равные минимуму из соответственных элементов каждой из двух частей, а во второй – равные максимуму. Утверждается, что получатся две битонные последовательности, каждую из которых можно рекурсивно отсортировать тем же образом, после чего можно склеить два массива (так как любой элемент первого меньше или равен любого элемента второго). Для того, чтобы преобразовать исходный массив в битонную последовательность, сделаем следующее: если массив состоит из двух элементов, можно просто завершиться, иначе разделим массив пополам, рекурсивно вызовем от половинок алгоритм, после чего отсортируем первую часть по порядку, вторую в обратном порядке и склеим. Очевидно, получится битонная последовательность. Асимптотика: O(nlog 2 n), поскольку при построении битонной последовательности мы использовали сортировку, работающую за O(nlogn), а всего уровней было logn. Также заметим, что размер массива должен быть равен степени двойки, так что, возможно, придется его дополнять фиктивными элементами (что не влияет на асимптотику).

Timsort

Гибридная сортировка, совмещающая сортировку вставками и сортировку слиянием. Разобьем элементы массива на несколько подмассивов небольшого размера, при этом будем расширять подмассив, пока элементы в нем отсортированы. Отсортируем подмассивы сортировкой вставками, пользуясь тем, что она эффективно работает на отсортированных массивах. Далее будем сливать подмассивы как в сортировке слиянием, беря их примерно равного размера (иначе время работы приблизится к квадратичному). Для этого удобного хранить подмассивы в стеке, поддерживая инвариант — чем дальше от вершины, тем больше размер, и сливать подмассивы на верхушке только тогда, когда размер третьего по отдаленности от вершины подмассива больше или равен сумме их размеров. Асимптотика: O(n) в лучшем случае и O(nlogn) в среднем и худшем случае. Реализация нетривиальна, твердой уверенности в ней у меня нет, однако время работы она показала довольно неплохое и согласующееся с моими представлениями о том, как должна работать эта сортировка.

Подробнее timsort описан здесь:

Тестирование

Железо и система

Процессор: Intel Core i7-3770 CPU 3.40 GHz
ОЗУ: 8 ГБ
Тестирование проводилось на почти чистой системе Windows 10 x64, установленной за несколько дней до запуска. Использованная IDE – Microsoft Visual Studio 2015.

Тесты

Все тесты поделены на четыре группы. Первая группа – массив случайных чисел по разным модулям (10, 1000, 10 5 , 10 7 и 10 9 ). Вторая группа – массив, разбивающийся на несколько отсортированных подмассивов. Фактически брался массив случайных чисел по модулю 10 9 , а далее отсортировывались подмассивы размера, равного минимуму из длины оставшегося суффикса и случайного числа по модулю некоторой константы. Последовательность констант – 10, 100, 1000 и т.д. вплоть до размера массива. Третья группа – изначально отсортированный массив случайных чисел с некоторым числом «свопов» — перестановок двух случайных элементов. Последовательность количеств свопов такая же, как и в предыдущей группе. Наконец, последняя группа состоит из нескольких тестов с полностью отсортированным массивом (в прямом и обратном порядке), нескольких тестов с исходным массивом натуральных чисел от 1 до n, в котором несколько чисел заменены на случайное, и тестов с большим количеством повторений одного элемента (10%, 25%, 50%, 75% и 90%). Таким образом, тесты позволяют посмотреть, как сортировки работают на случайных и частично отсортированных массивах, что выглядит наиболее существенным. Четвертая группа во многом направлена против сортировок с линейным временем работы, которые любят последовательности случайных чисел. В конце статьи есть ссылка на файл, в котором подробно описаны все тесты.

Размер входных данных

Было бы довольно глупо сравнивать, например, сортировку с линейным временем работы и квадратичную, и запускать их на тестах одного размера. Поэтому каждая из групп тестов делится еще на четыре группы, размера 10 5 , 10 6 , 10 7 и 10 8 элементов. Сортировки были разбиты на три группы, в первой – квадратичные (сортировка пузырьком, вставками, выбором, шейкерная и гномья), во второй – нечто среднее между логарифмическим временем и квадратом, (битонная, несколько видов сортировки Шелла и сортировка деревом), в третьей все остальные. Кого-то, возможно, удивит, что сортировка деревом попала не в третью группу, хотя ее асимптотика и O(nlogn), но, к сожалению, ее константа очень велика. Сортировки первой группы тестировались на тестах с 10 5 элементов, второй группы – на тестах с 10 6 и 10 7 , третьей – на тестах с 10 7 и 10 8 . Именно такие размеры данных позволяют как-то увидеть рост времени работы, при меньших размерах слишком велика погрешность, при больших алгоритм работает слишком долго (или же недостаток оперативной памяти). С первой группой я не стал заморачиваться, чтобы не нарушать десятикратное увеличение (10 4 элементов для квадратичных сортировок слишком мало), в конце концов, сами по себе они представляют мало интереса.

Как проводилось тестирование

На каждом тесте было производилось 20 запусков, итоговое время работы – среднее по получившимся значениям. Почти все результаты были получены после одного запуска программы, однако из-за нескольких ошибок в коде и системных глюков (все же тестирование продолжалось почти неделю чистого времени) некоторые сортировки и тесты пришлось впоследствии перетестировать.

Тонкости реализации

Возможно, кого-то удивит, что в реализации самого процесса тестирования я не использовал указатели на функции, что сильно сократило бы код. Оказалось, что это заметно замедляет работу алгоритма (примерно на 5-10%). Поэтому я использовал отдельный вызов каждой функции (это, конечно, не отразилось бы на относительной скорости, но… все же хочется улучшить и абсолютную). По той же причине были заменены векторы на обычные массивы, не были использованы шаблоны и функции-компараторы. Все это более актуально для промышленного использования алгоритма, нежели его тестирования.

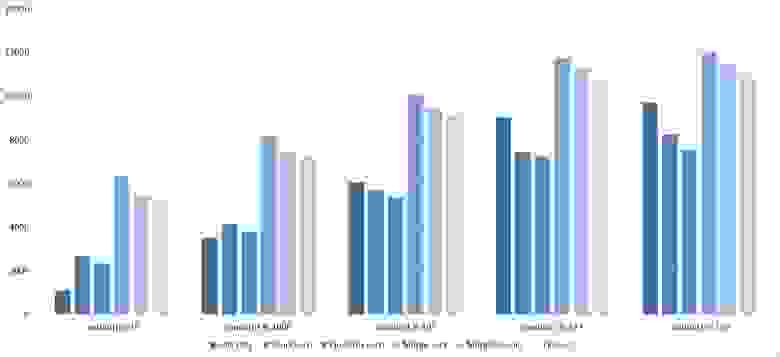
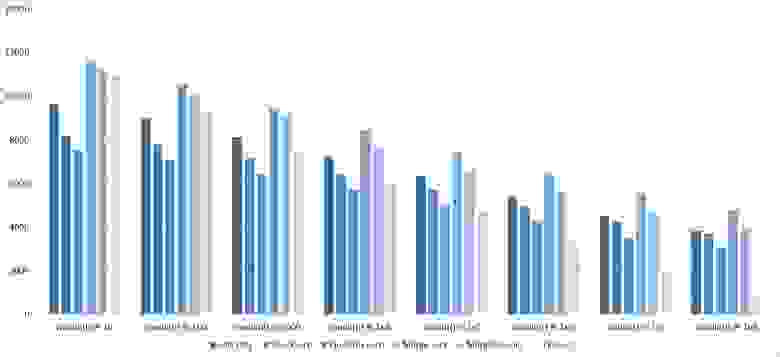
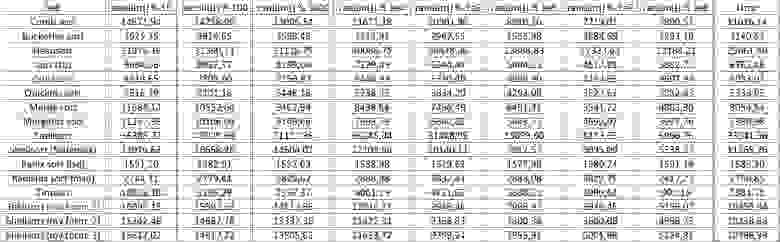
Результаты

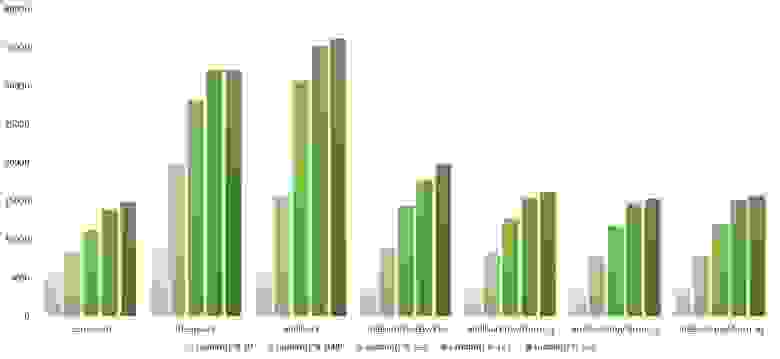
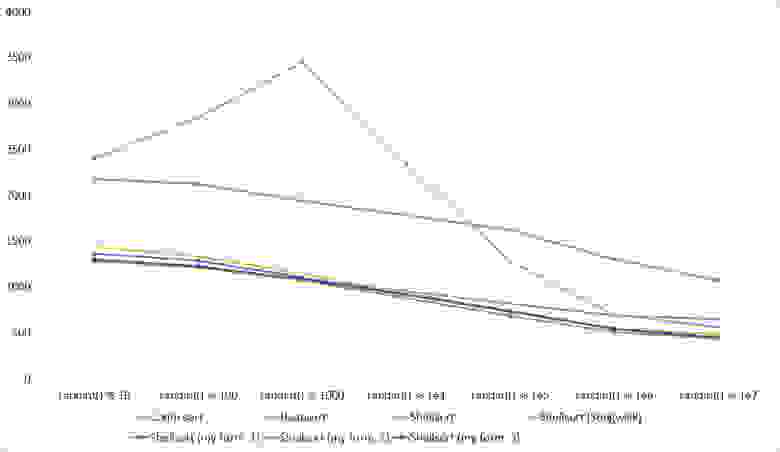
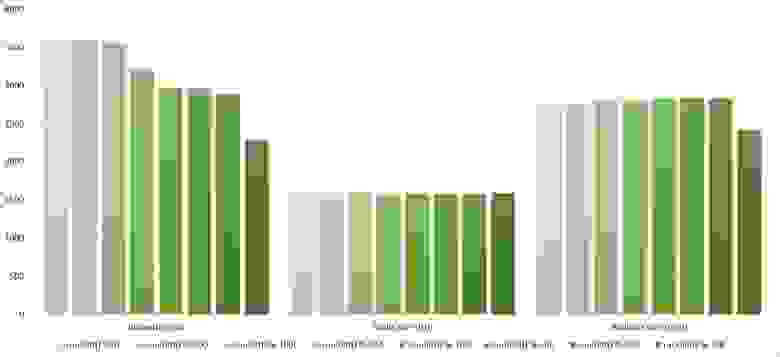
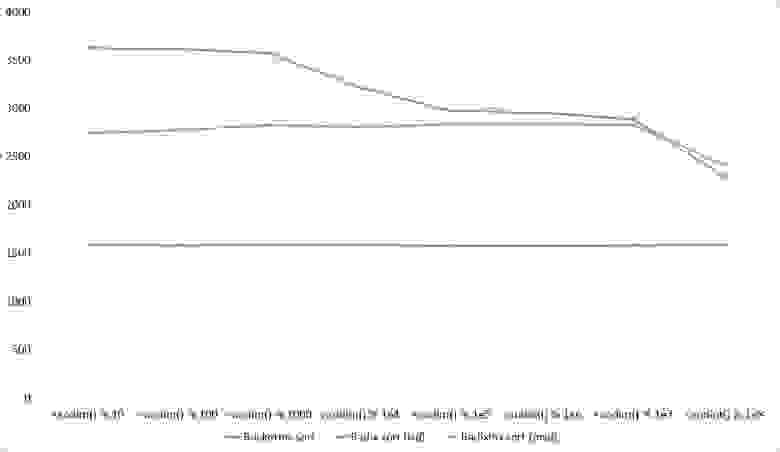
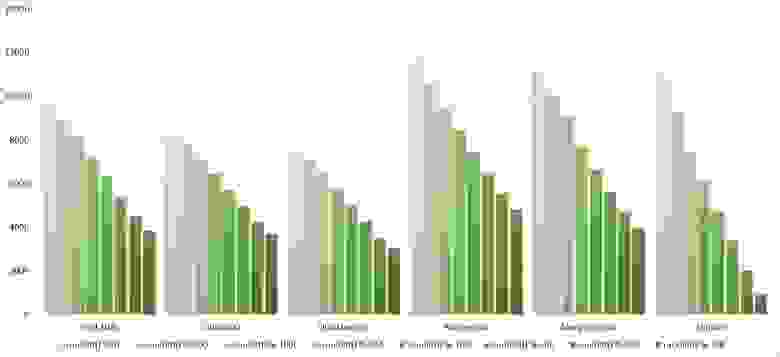
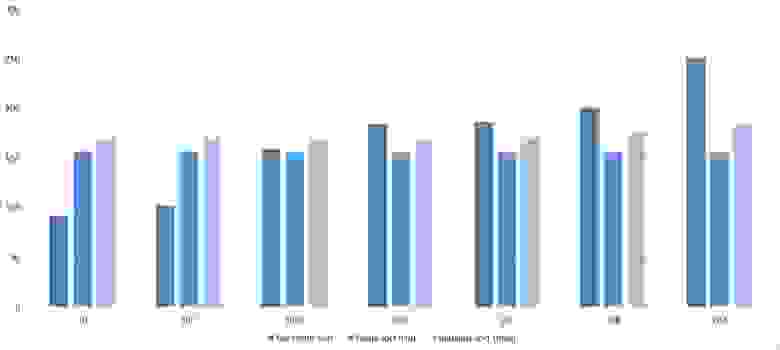
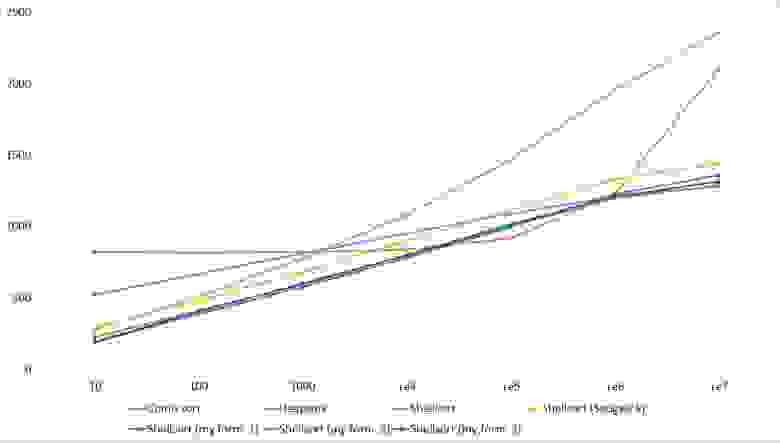
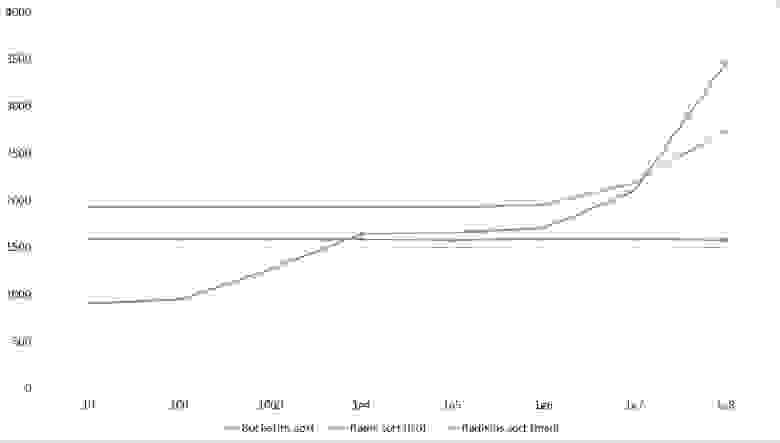
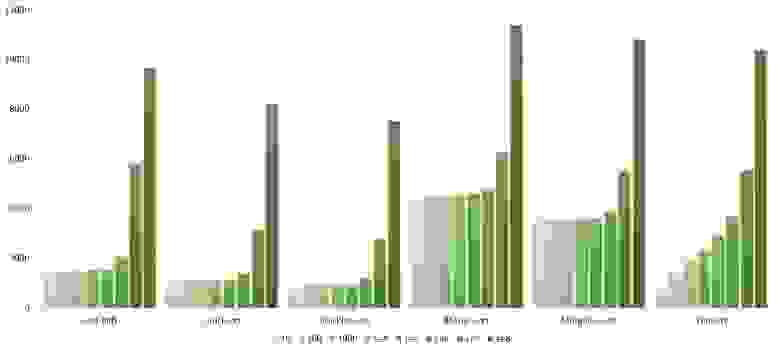
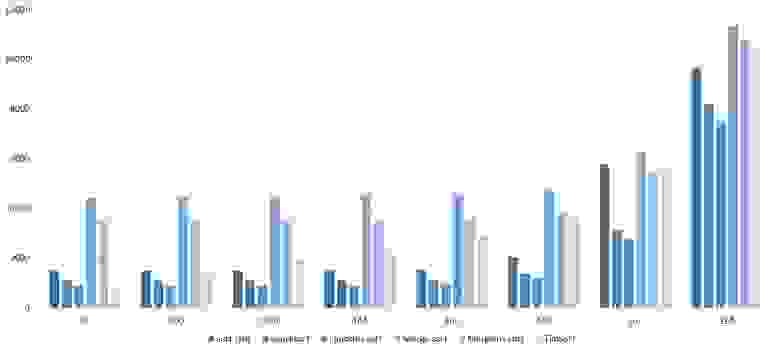
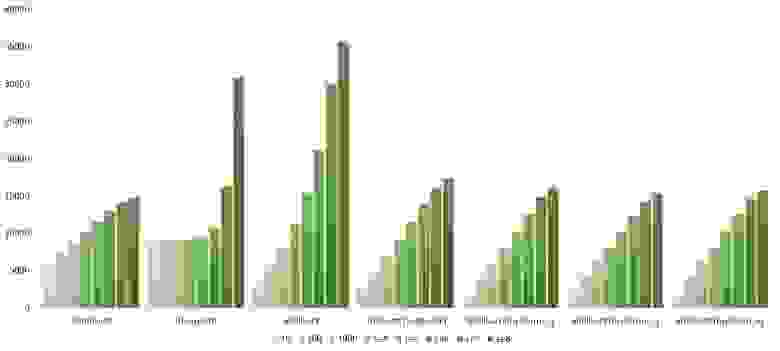
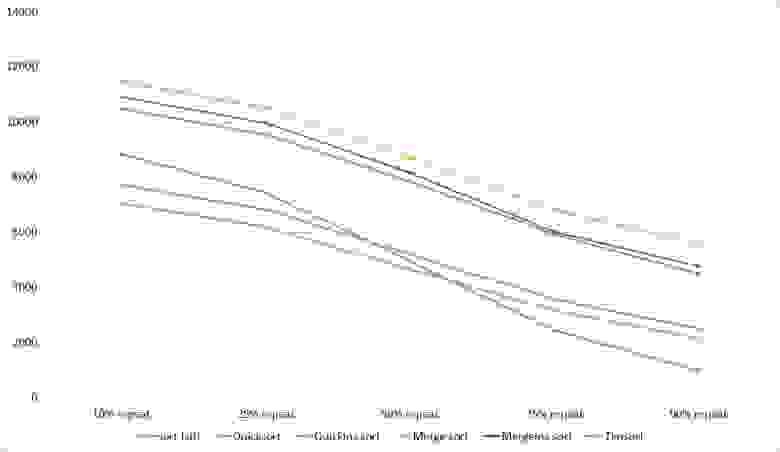
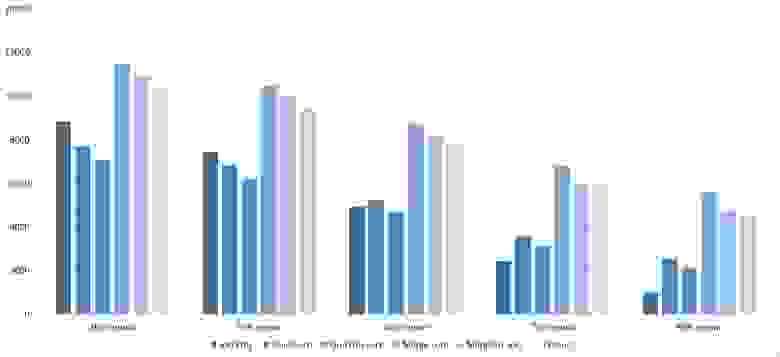
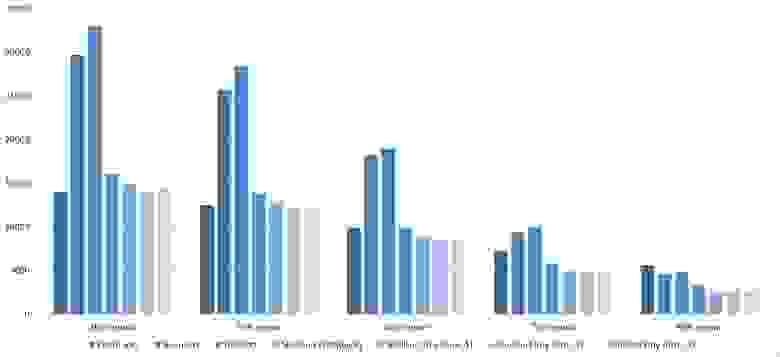
Все результаты доступны в нескольких видах – три диаграммы (гистограмма, на которой видно изменение скорости при переходе к следующему ограничению на одном типе тестов, график, изображающий то же самое, но иногда более наглядно, и гистограмма, на которой видно, какая сортировка лучше всего работает на каком-то типе тестов) и таблицы, на которых они основаны. Третья группа была разделена еще на три части, а то мало что было бы понятно. Впрочем, и так далеко не все диаграммы удачны (в полезности третьего типа диаграмм я вообще сильно сомневаюсь), но, надеюсь, каждый сможет найти наиболее подходящую для понимания.

Поскольку картинок очень много, они скрыты спойлерами. Немного комментариев по поводу обозначений. Сортировки названы так, как выше, если это сортировка Шелла, то в скобочках указан автор последовательности, к названиям сортировок, переходящих на сортировку вставками, приписано Ins (для компактности). В диаграммах у второй группы тестов обозначена возможная длина отсортированных подмассивов, у третьей группы — количество свопов, у четвертой — количество замен. Общий результат рассчитывался как среднее по четырем группам.

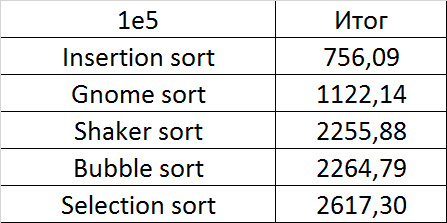
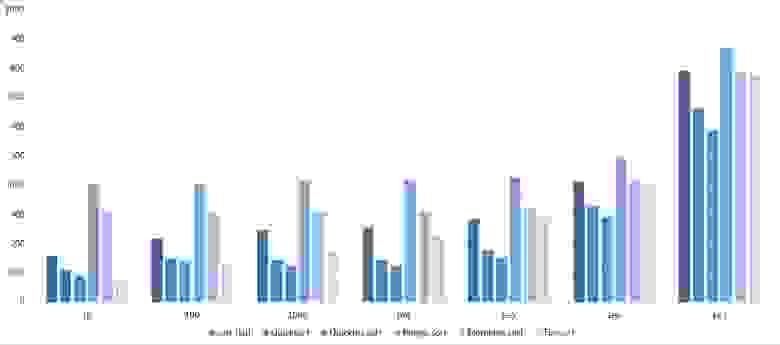
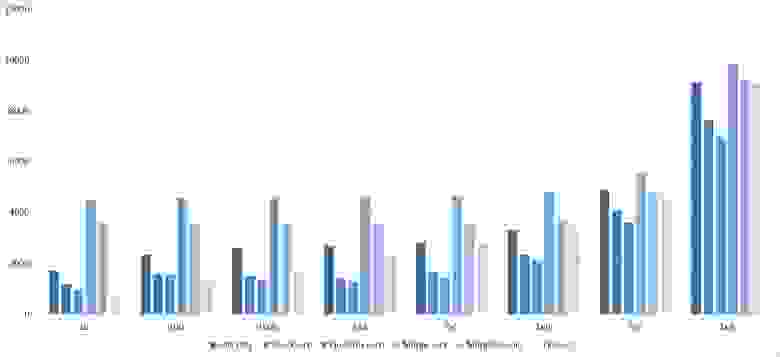
Первая группа сортировок

Массив случайных чисел

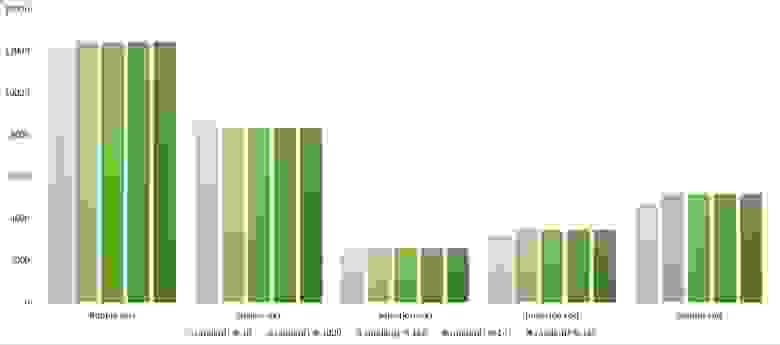
Совсем скучные результаты, даже частичная отсортированность при небольшом модуле почти незаметна.

Частично отсортированный массив

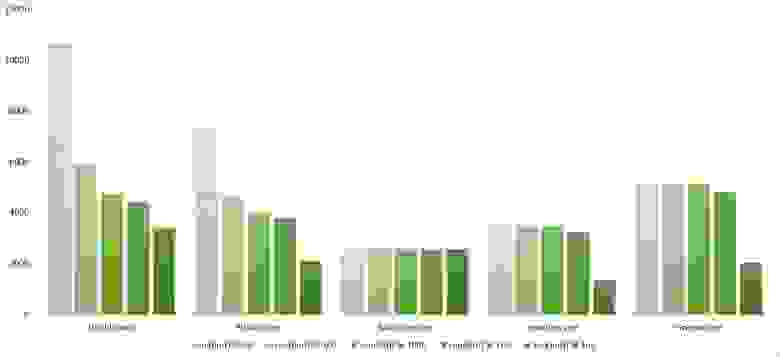
Уже гораздо интереснее. Обменные сортировки наиболее бурно отреагировали, шейкерная даже обогнала гномью. Сортировка вставками ускорилась только под самый конец. Сортировка выбором, конечно, работает совершенно также.

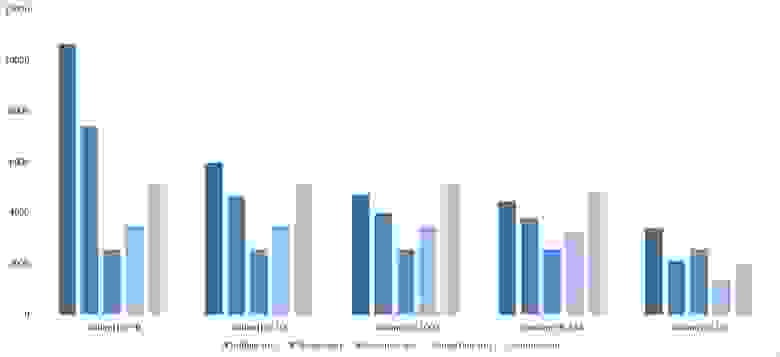
Свопы

Здесь наконец-то проявила себя сортировка вставками, хотя рост скорости у шейкерной примерно такой же. Здесь проявилась слабость сортировки пузырьком — достаточно одного свопа, перемещающего маленький элемент в конец, и она уже работает медленно. Сортировка выбором оказалась почти в конце.

Изменения в перестановке

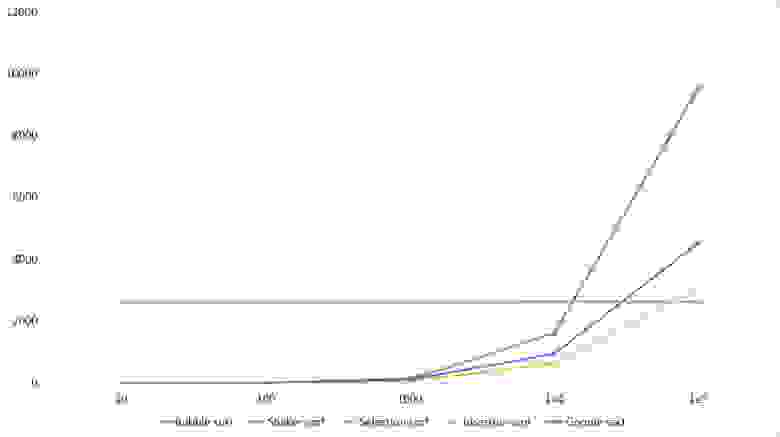
Группа почти ничем не отличается от предыдущей, поэтому результаты похожи. Однако сортировка пузырьком вырывается вперед, так как случайный элемент, вставленный в массив, скорее всего будет больше всех остальных, то есть за одну итерацию переместится в конец. Сортировка выбором стала аутсайдером.

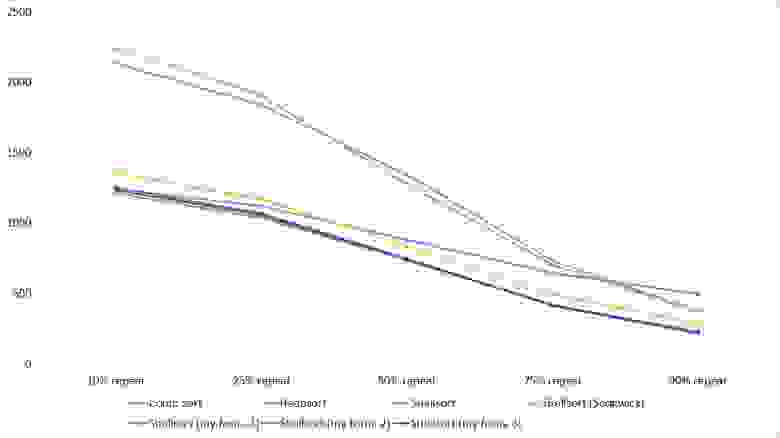
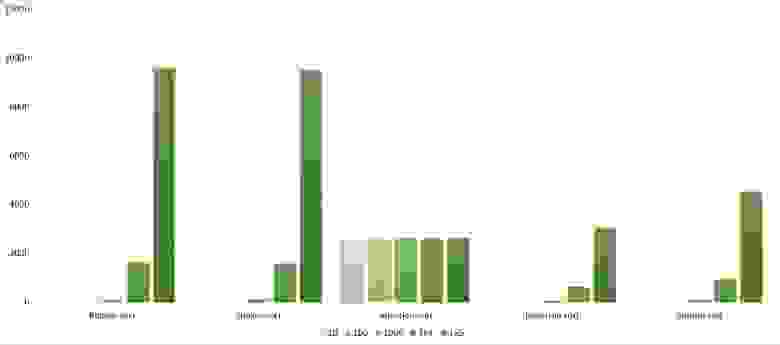
Повторы

Здесь все сортировки (кроме, конечно, сортировки выбором) работали почти одинаково, ускоряясь по мере увеличении количества повторов.

Итоговые результаты

За счет своего абсолютного безразличия к массиву, сортировка выбором, работавшая быстрее всех на случайных данных, все же проиграла сортировке вставками. Гномья сортировка оказалась заметно хуже последней, из-за чего ее практическое применение сомнительно. Шейкерная и пузырьковая сортировки оказались медленнее всех.

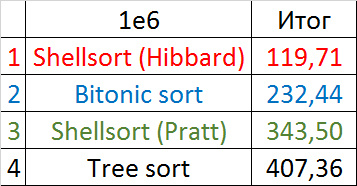
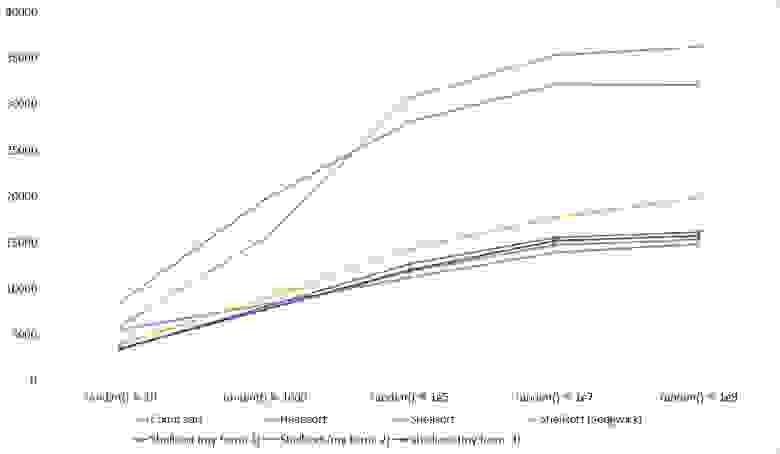
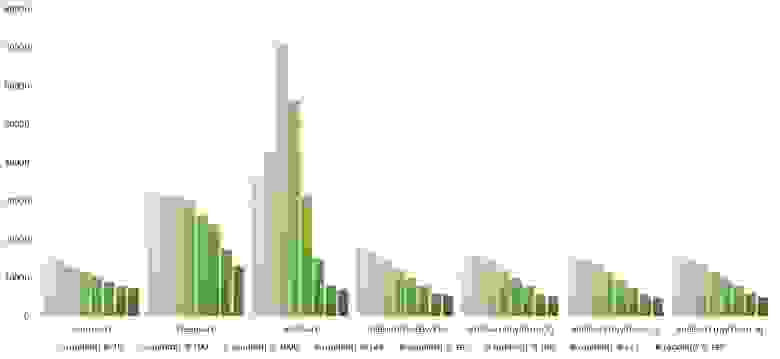
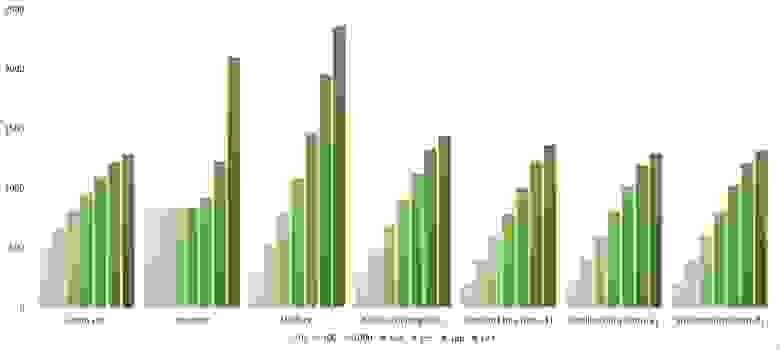
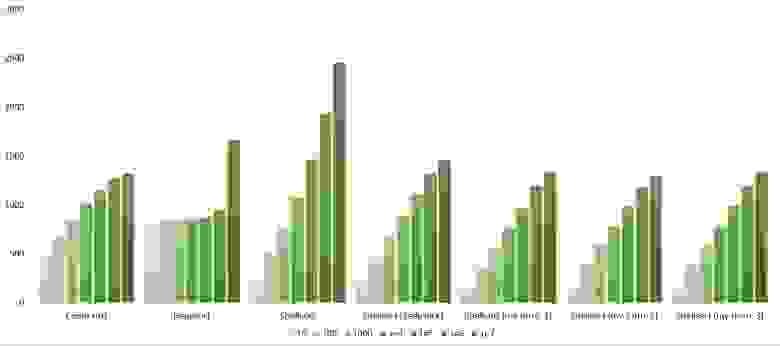
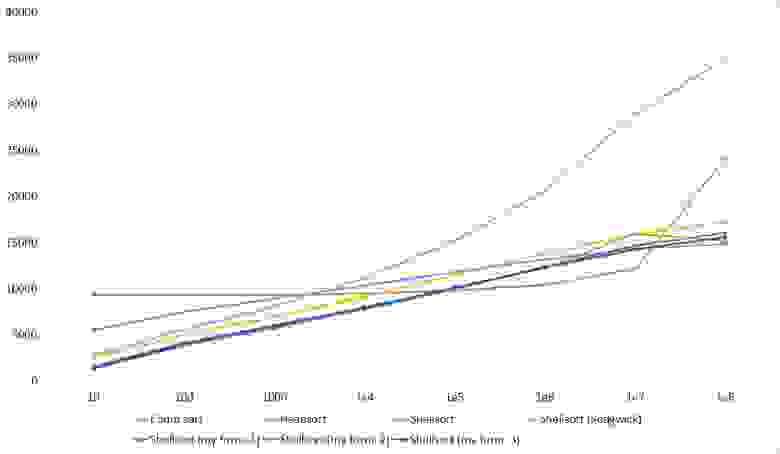
Вторая группа сортировок

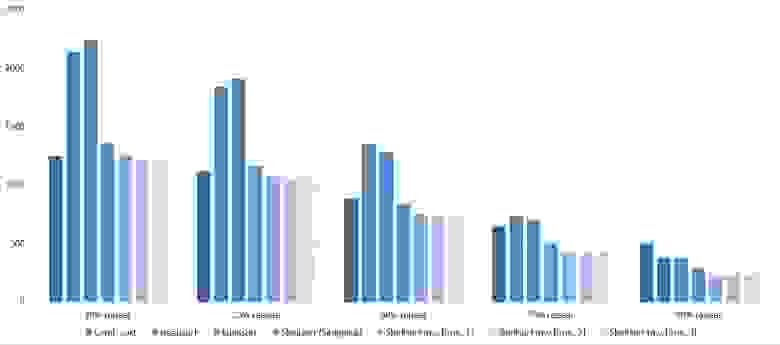
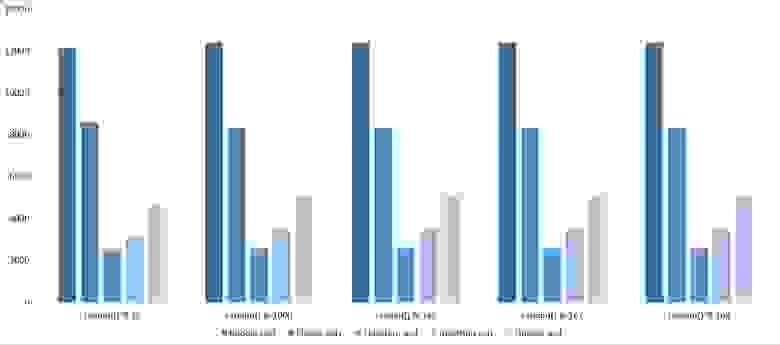
Массив случайных чисел

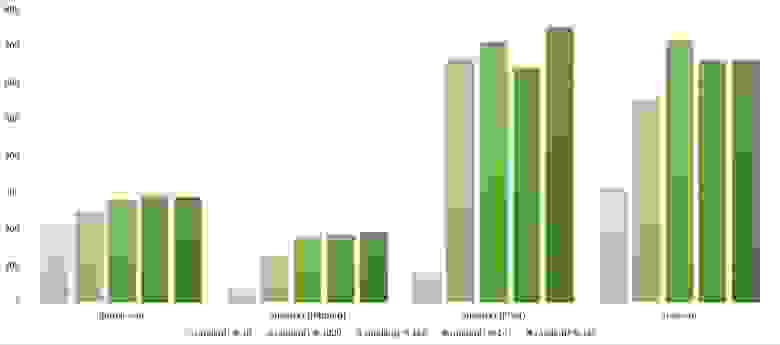
Сортировка Шелла с последовательностью Пратта ведет себя совсем странно, остальные более менее ясно. Сортировка деревом любит частично отсортированные массивы, но не любит повторов, возможно, поэтому самое худшее время работы именно посередине.

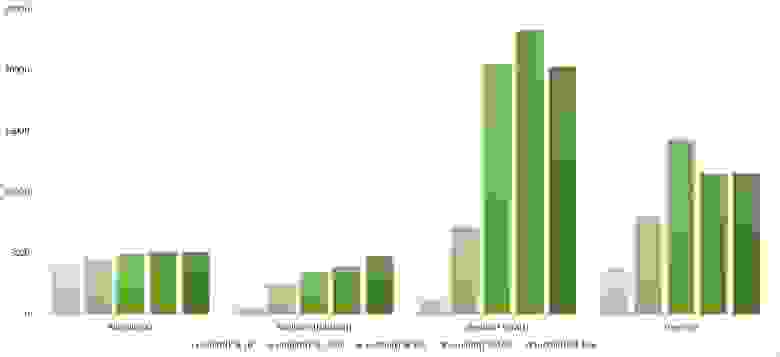
Все как прежде, только Шелл с Праттом усилился на второй группе из-за отсортированности. Также становится заметным влияние асимптотики — сортировка деревом оказывается на втором месте, в отличие от группы с меньшим числом элементов.

Частично отсортированный массив

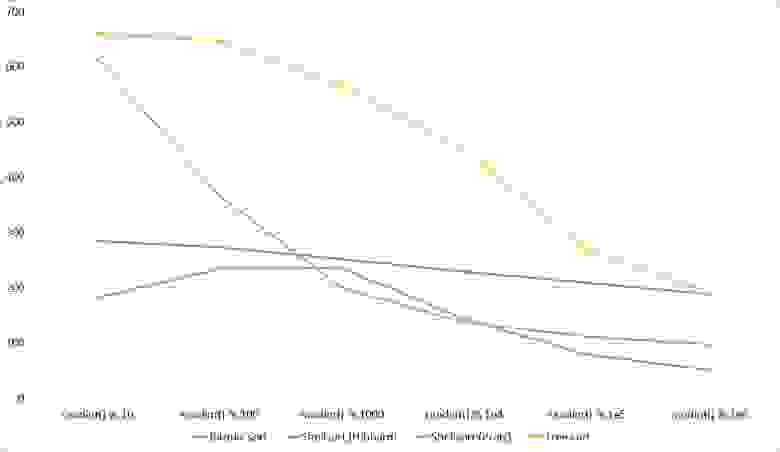
Здесь понятным образом ведут себя все сортировки, кроме Шелла с Хиббардом, который почему-то не сразу начинает ускоряться.

Здесь все, в общем, как и прежде. Даже асимптотика сортировки деревом не помогла ей вырваться с последнего места.

Свопы

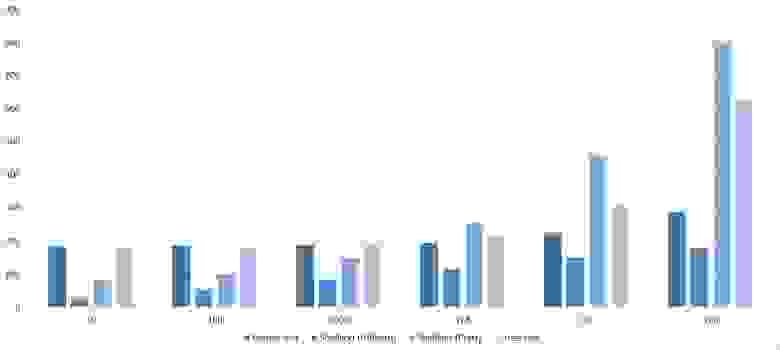
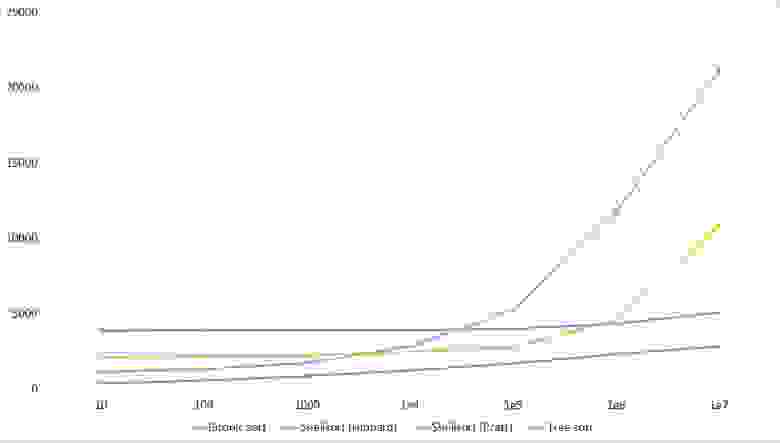
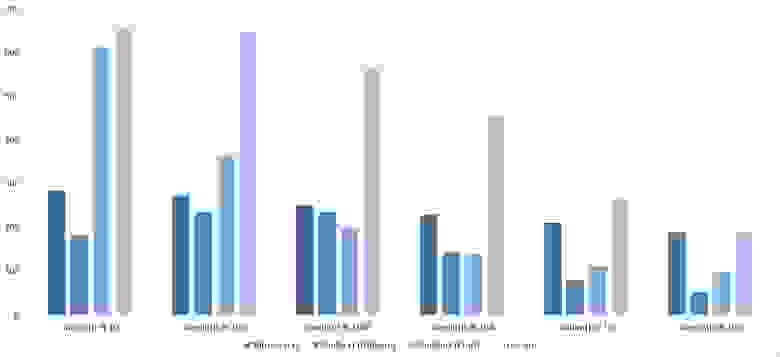
Здесь заметно, что у сортировок Шелла большая зависимость от частичной отсортированности, так как они ведут себя практически линейно, а остальные две только сильно падают на последних группах.

Изменения в перестановке

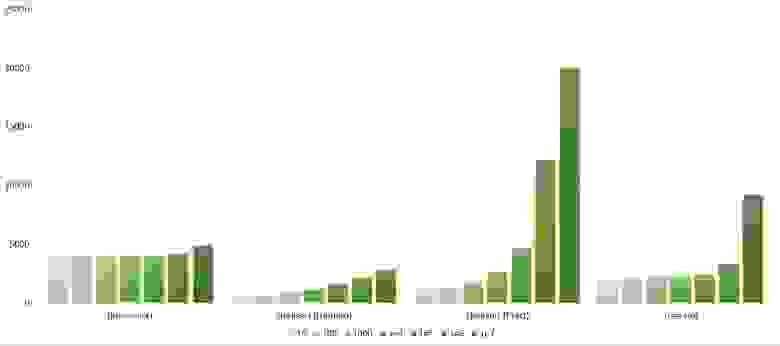
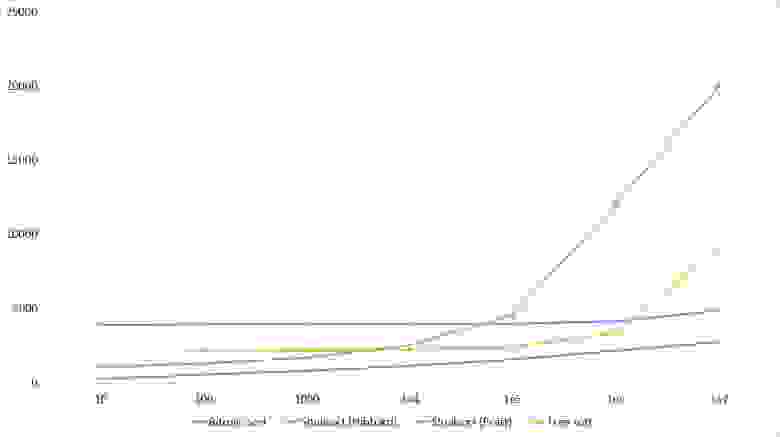
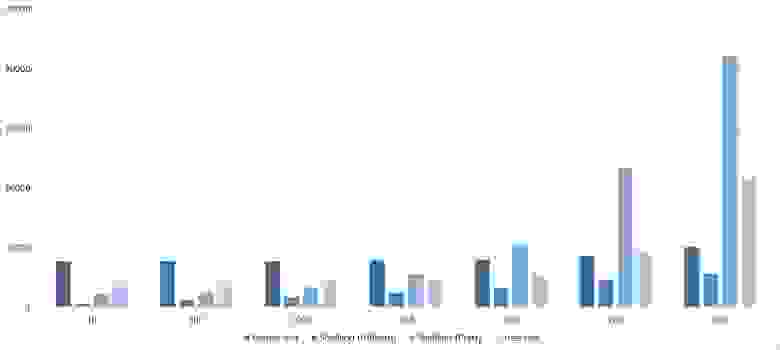
Здесь все похоже на предыдущую группу.

Повторы

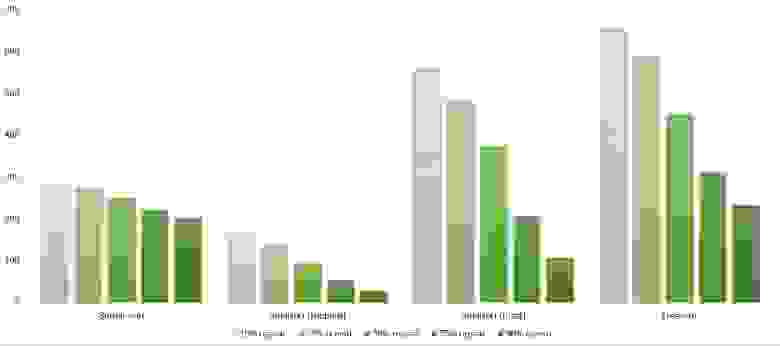
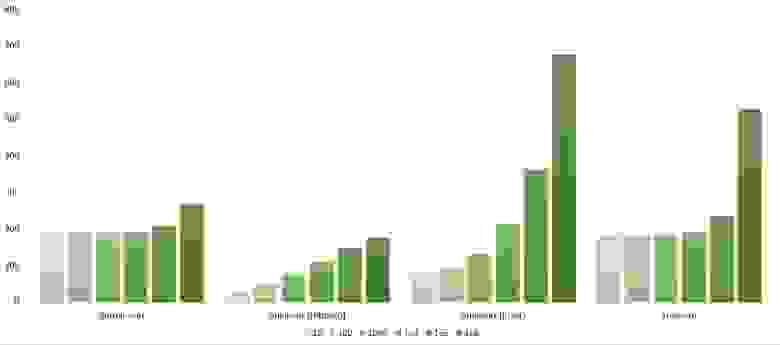
Опять все сортировки продемонстрировали удивительную сбалансированность, даже битонная, которая, казалось бы, почти не зависит от массива.

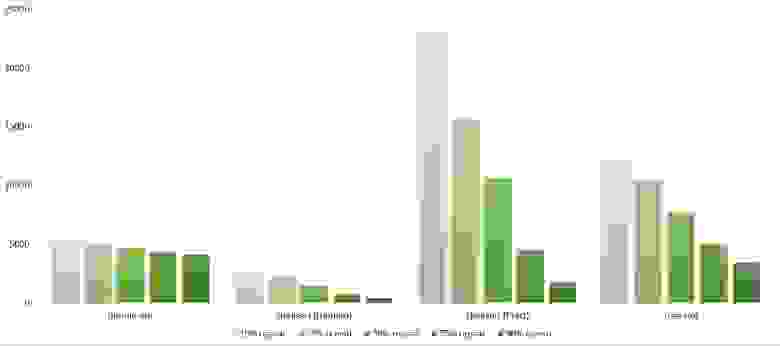
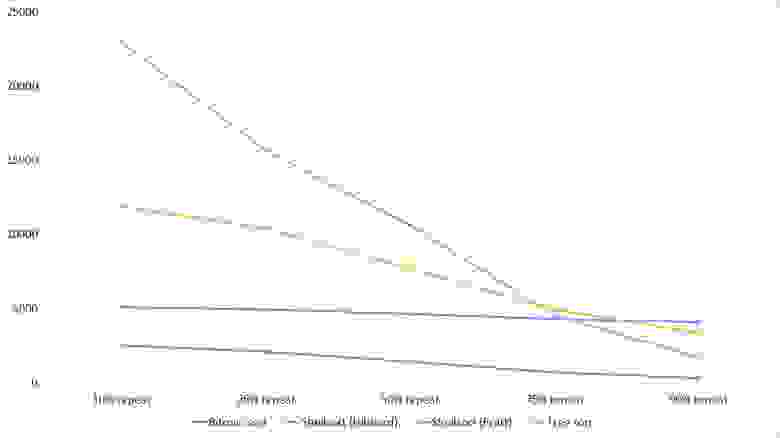
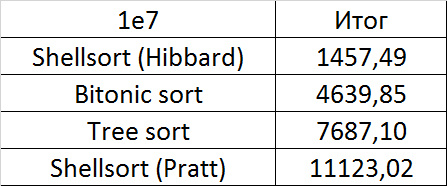
Итоговые результаты

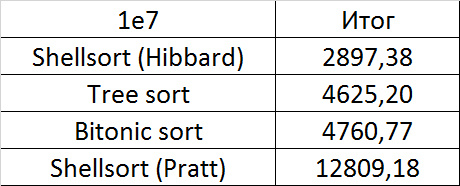
Убедительное первое место заняла сортировка Шелла по Хиббарду, не уступив ни в одной промежуточной группе. Возможно, стоило ее отправить в первую группу сортировок, но… она слишком слаба для этого, да и тогда почти никого не было бы в группе. Битонная сортировка довольно уверенно заняла второе место. Третье место при миллионе элементах заняла другая сортировка Шелла, а при десяти миллионах сортировка деревом (асимптотика сказалась). Стоит обратить внимание, что при десятикратном увеличении размера входных данных все алгоритмы, кроме древесной сортировки, замедлились почти в 20 раз, а последняя всего лишь в 13.

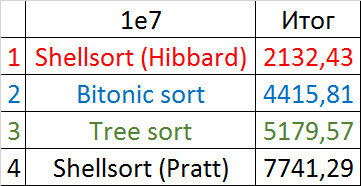
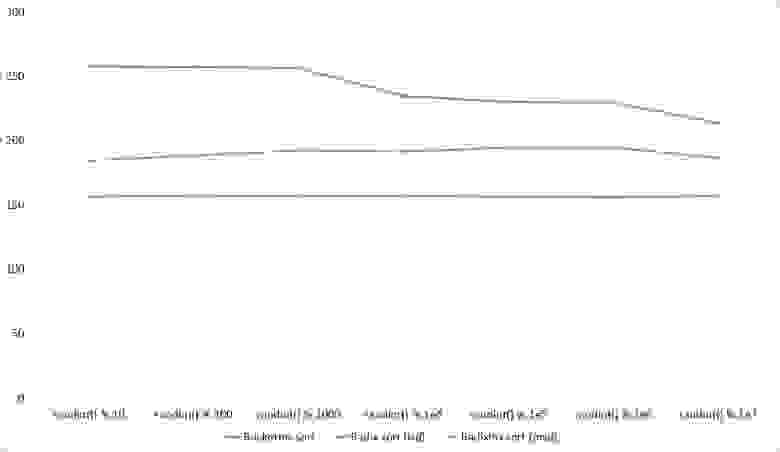
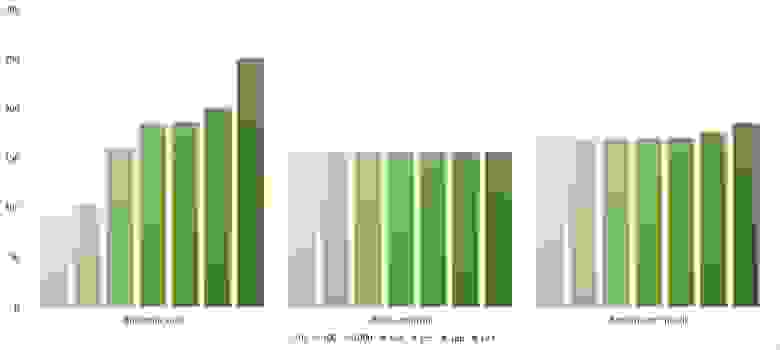
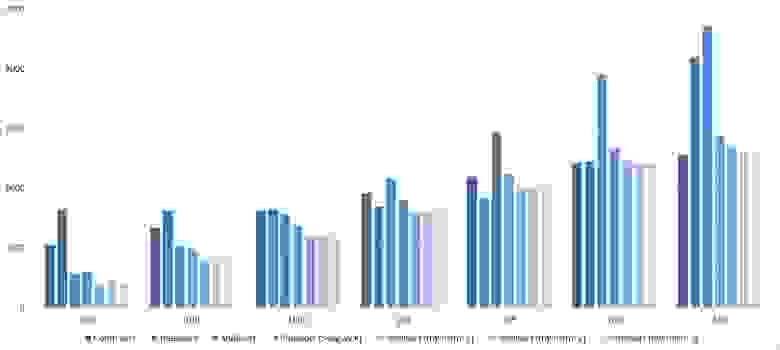
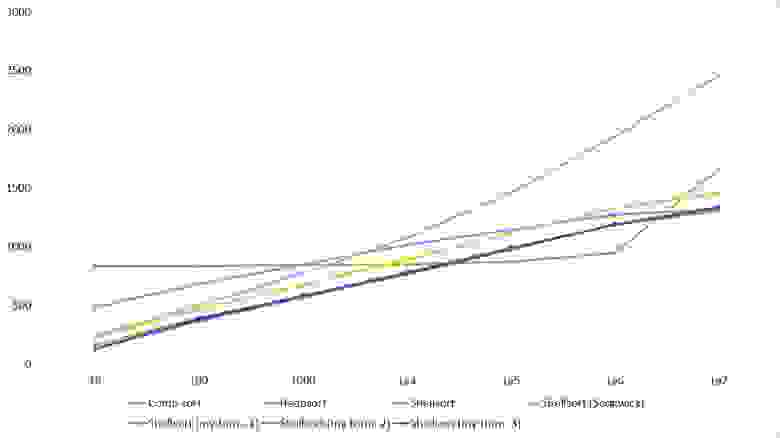
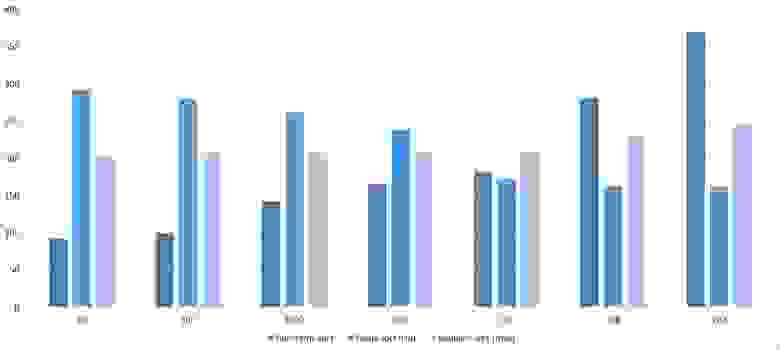
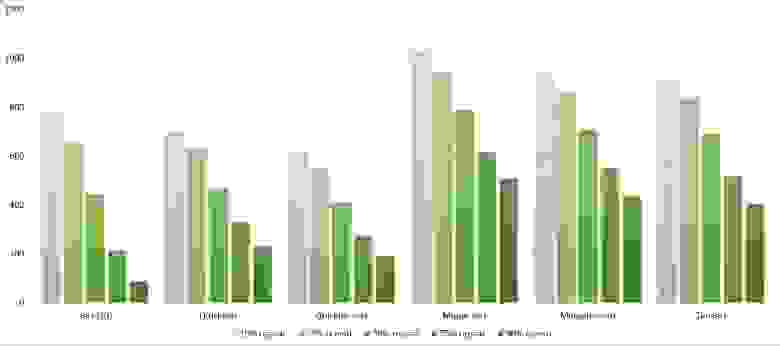
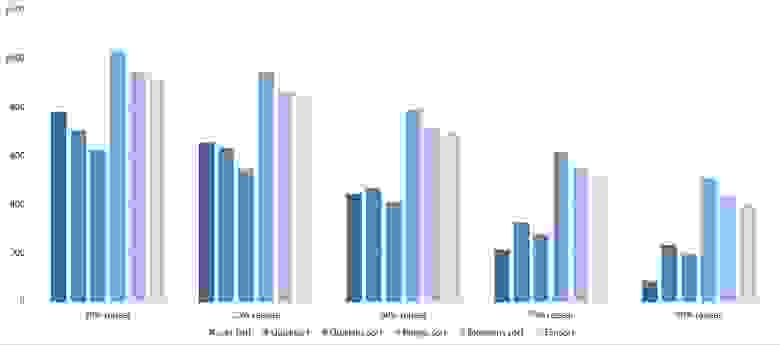
Третья группа сортировок

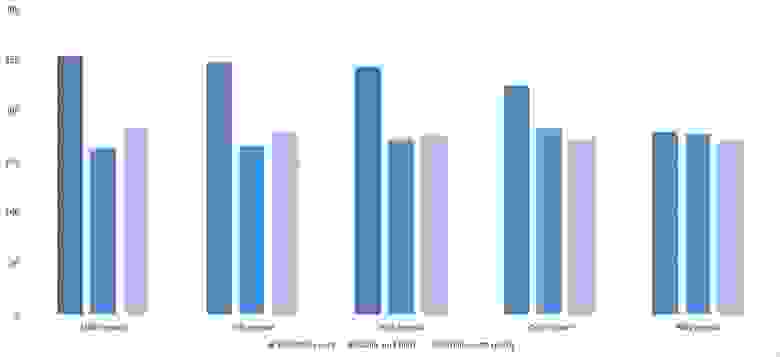
Массив случайных чисел

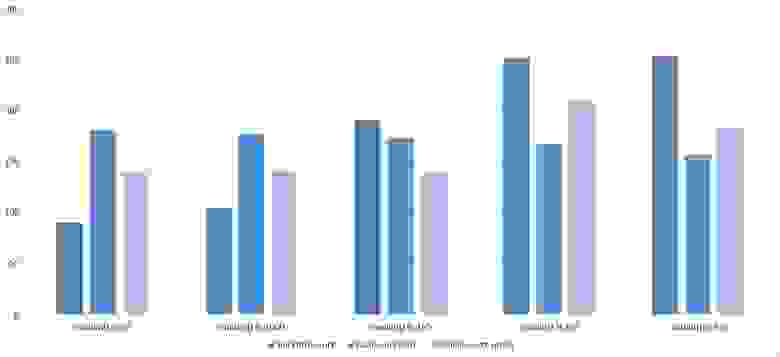
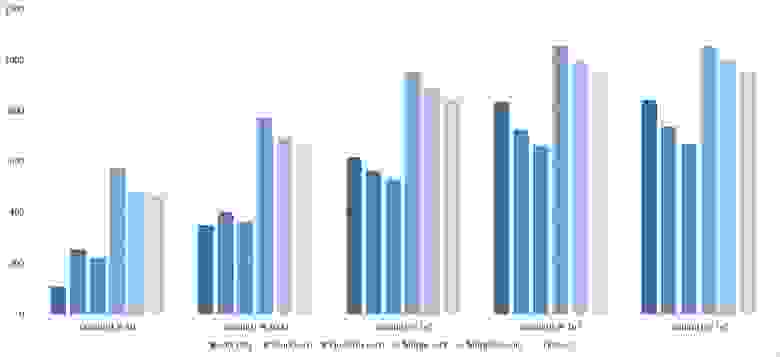
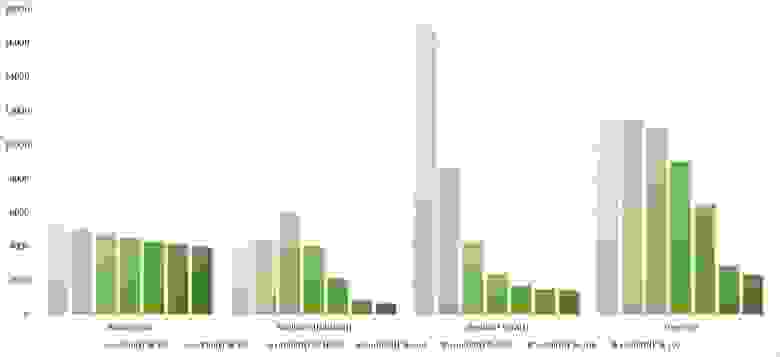
Почти все сортировки этой группы имеют почти одинаковую динамику. Почему же почти все сортировки ускоряются, когда массив частично отсортирован? Обменные сортировки работают быстрее потому, что надо делать меньше обменов, в сортировке Шелла выполняется сортировка вставками, которая сильно ускоряется на таких массивах, в пирамидальной сортировке при вставке элементов сразу завершается просеивание, в сортировке слиянием выполняется в лучшем случае вдвое меньше сравнений. Блочная сортировка работает тем лучше, чем меньше разность между минимальным и максимальным элементом. Принципиально отличается только поразрядная сортировка, которой все это безразлично. LSD-версия работает тем лучше, чем больший модуль. Динамика MSD-версия мне не ясна, то, что она сработала быстрее чем LSD удивило.

Частично отсортированный массив

Здесь все тоже довольно понятно. Стало заметен алгоритм Timsort, на него отсортированность действует сильнее, чем на остальные. Это позволило этому алгоритму почти сравняться с оптимизированной версией быстрой сортировки. Блочная сортировка, несмотря на улучшение времени работы при частичной отсортированности, не смогла обогнать поразрядную сортировку.

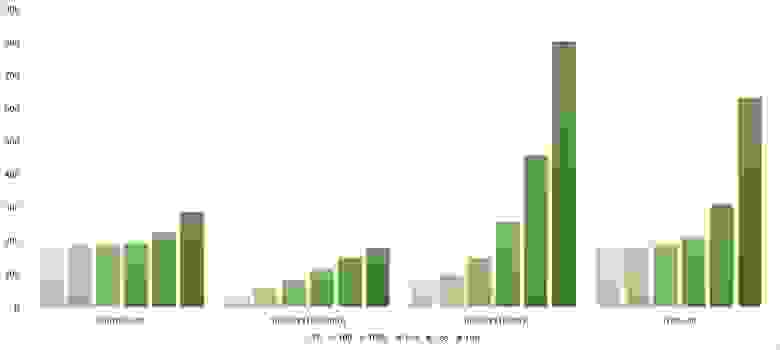
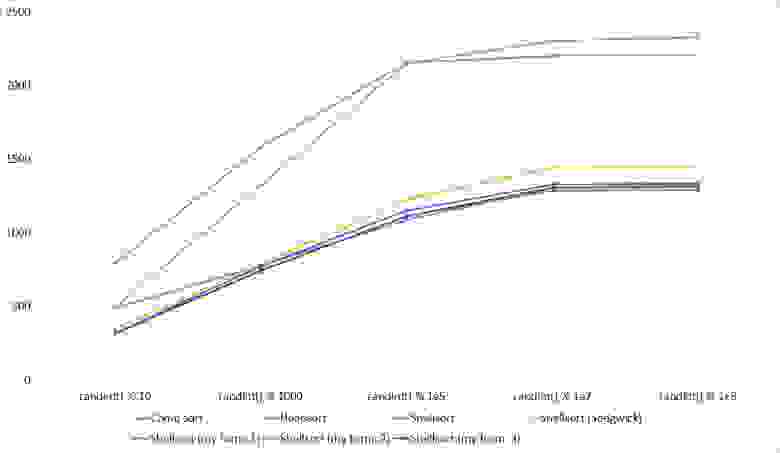
Свопы

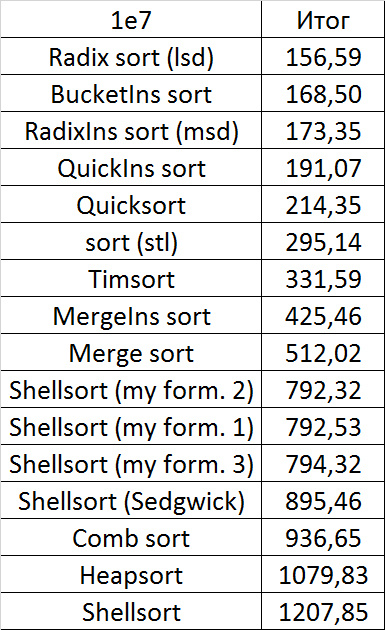
Здесь очень хорошо сработали быстрые сортировки. Это, скорее всего, объясняется удачным выбором опорного элемента. Все остальное почти также, как и в предыдущей группе.

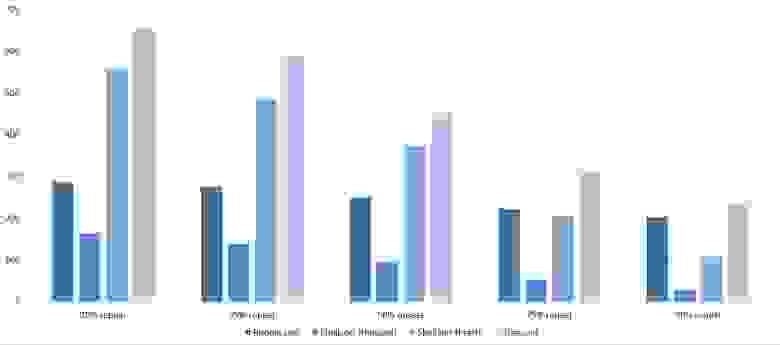
Изменения в перестановке

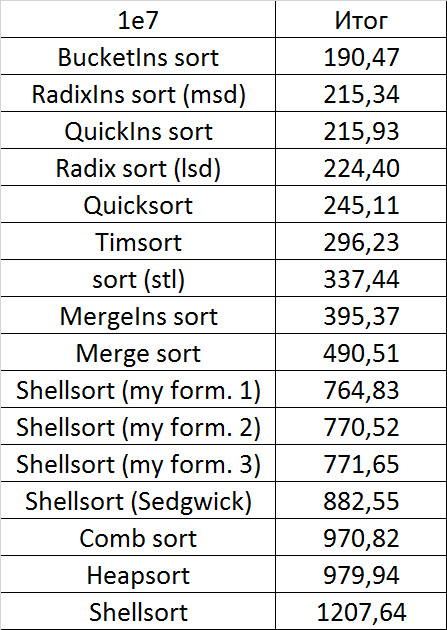
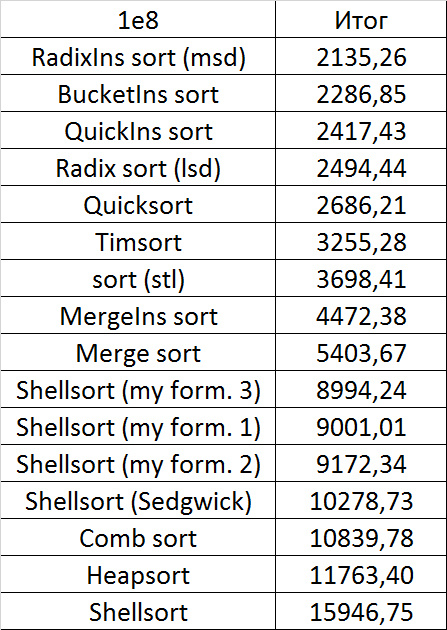
Мне удалось достичь желаемой цели — поразрядная сортировка упала даже ниже адаптированной быстрой. Блочная сортировка оказалась лучше остальных. Еще почему-то timsort обогнал встроенную сортировку C++, хотя в предыдущей группе был ниже.

Повторы

Здесь все довольно тоскливо, все сортировки работают с одинаковой динамикой (кроме линейных). Из необычного можно заметить, что сортировка слиянием упала ниже сортировки Шелла.

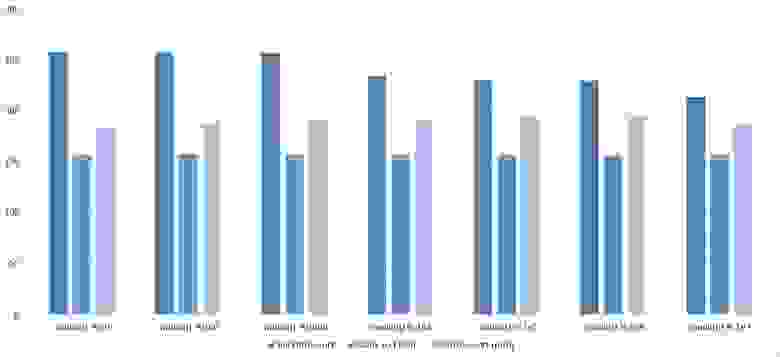
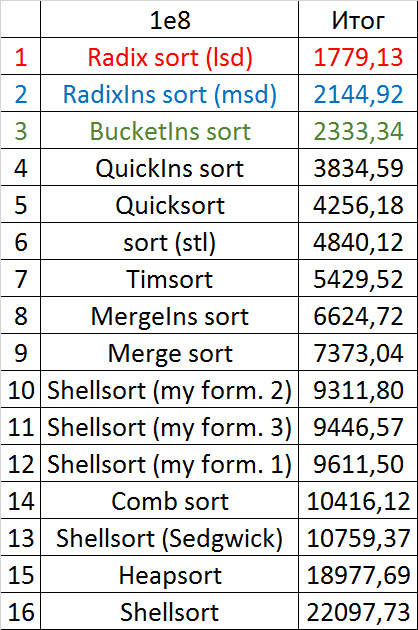
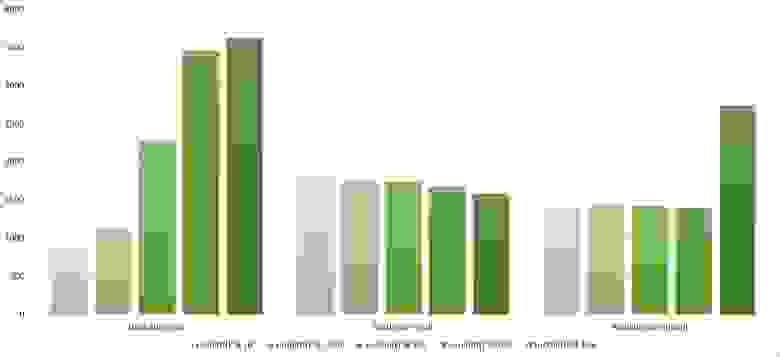
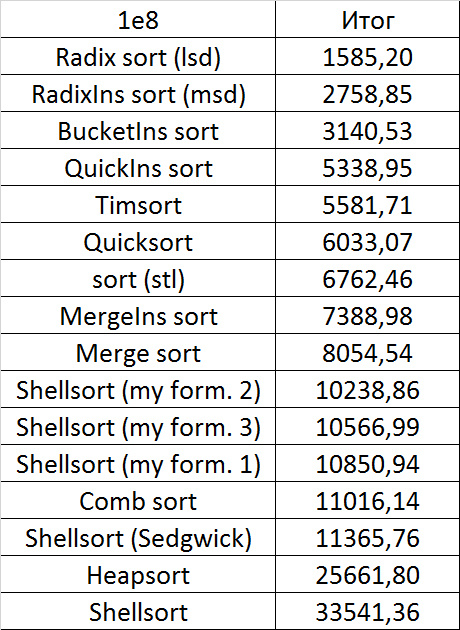
Итоговые результаты

Несмотря на мои старания, LSD-версия поразрядной сортировки все-таки заняла первое место и при 10 7 , и при 10 8 элементов. Также она продемонстрировала почти линейный рост времени. Единственная ее замеченная мной слабость — плохая работа с перестановками. MSD-версия сработала немного хуже, в первую очередь из-за большого количества тестов, состоящих из случайных чисел по модулю 10 9 . Реализацией блочной сортировки я остался доволен, несмотря на громоздкость, она показало неплохой результат. Кстати, я слишком поздно это заметил, она не до конца соптимизирована, можно еще отдельно создавать массивы run и cnt, чтобы не тратить время на их удаление. Далее уверенно заняли места различные версии быстрой сортировки. Timsort-у не удалось, на мой взгляд, оказать им серьезную конкуренцию, хотя он не сильно отстал. Далее по скорости идут сортировки слиянием, после них — мои версии сортировки Шелла. Лучше всего оказалась последовательность s * 3 + s / 3, где s — предыдущий элемент последовательности. Далее идет единственное расхождение в двух таблицах — сортировка расческой оказалась лучше при большем числе элементов, чем сортировка Шелла с последовательностью Седжвика. И за последнее место боролись пирамидальная сортировка и оригинальная сортировка Шелла.

Выиграла последняя. Кстати, сортировка Шелла, как я потом проверил, очень плохо работает на тестах размера 2 n , так что ей просто повезло, что она попала в первую группу.

Если говорить о практическом применении, то хороша поразрядная сортировка (особенно lsd-версия), она стабильна, проста в реализации и очень быстра, однако не основана на сравнениях. Из основанных на сравнениях сортировок лучше всего смотрится быстрая сортировка. Ее недостатки — неустойчивость и квадратичное время работы на неудачных входных данных (пусть они и могут встретиться только при намеренном создании теста). Но с этим можно бороться, например, выбирая опорный элемент по какому-нибудь другому принципу, или же переходя на другую сортировку при неудаче (например, introsort, который, если не ошибаюсь, и реализован в С++). Timsort лишен этих недостатков, лучше работает на сильно отсортированных данных, но все же медленнее в целом и гораздо сложнее пишется. Остальные сортировки на данный момент, пожалуй, не очень практичны. Кроме, конечно, сортировки вставками, которую весьма удачно иногда можно вставить в алгоритм.

Заключение

Должен отметить, что не все известные сортировки приняли участие в тестировании, например, была пропущена плавная сортировка (мне просто не удалось ее адекватно реализовать). Впрочем, не думаю, что это большая потеря, эта сортировка очень громоздкая и медленная, как можно видеть, например, из этой статьи: habrahabr.ru/post/133996 Еще можно исследовать сортировки на распараллеливание, но, во-первых, у меня нет опыта, во-вторых, результаты, которые получались, крайне нестабильны, очень велико влияние системы.

Здесь можно посмотреть результаты всех запусков, а также некоторые вспомогательные тестирования: ссылка на документ.

Реализации алгоритмов с векторами остались, но их корректность и хорошую работу не гарантирую. Проще взять коды функций из статьи и переделать. Генераторы тестов тоже могут не соответствовать действительности, на самом деле такой вид они приняли уже после создания тестов, когда нужно было сделать программу более компактной.

В общем, я доволен проделанной работой, надеюсь, что Вам было интересно.

Источник