Способы сортировки массивов вставка

Сортировка вставками

Сортировка вставками (англ. Insertion sort) — квадратичный алгоритм сортировки.

Содержание

Алгоритм [ править ]

Задача заключается в следующем: есть часть массива, которая уже отсортирована, и требуется вставить остальные элементы массива в отсортированную часть, сохранив при этом упорядоченность. Для этого на каждом шаге алгоритма мы выбираем один из элементов входных данных и вставляем его на нужную позицию в уже отсортированной части массива, до тех пор пока весь набор входных данных не будет отсортирован. Метод выбора очередного элемента из исходного массива произволен, однако обычно (и с целью получения устойчивого алгоритма сортировки), элементы вставляются по порядку их появления во входном массиве.

Так как в процессе работы алгоритма могут меняться местами только соседние элементы, каждый обмен уменьшает число инверсий на единицу. Следовательно, количество обменов равно количеству инверсий в исходном массиве вне зависимости от реализации сортировки. Максимальное количество инверсий содержится в массиве, элементы которого отсортированы по невозрастанию. Число инверсий в таком массиве [math]\displaystyle \frac <2>[/math] .

Алгоритм работает за [math]O(n + k)[/math] , где [math]k[/math] — число обменов элементов входного массива, равное числу инверсий. В среднем и в худшем случае — за [math]O(n^2)[/math] . Минимальные оценки встречаются в случае уже упорядоченной исходной последовательности элементов, наихудшие — когда они расположены в обратном порядке.

Псевдокод [ править ]

Пример работы [ править ]

Пример работы алгоритма для массива [math][ 5, 2, 4, 3, 1 ][/math]

До	После	Описание шага
Первый проход (проталкиваем второй элемент — 2)
5 2 4 3 1	2 5 4 3 1	Алгоритм сравнивает второй элемент с первым и меняет их местами.
Второй проход (проталкиваем третий элемент — 4)
2 5 4 3 1	2 4 5 3 1	Сравнивает третий со вторым и меняет местами
2 4 5 3 1	2 4 5 3 1	Второй и первый отсортированы, swap не требуется
Третий проход (проталкиваем четвертый — 3)
2 4 5 3 1	2 4 3 5 1	Меняет четвертый и третий местами
2 4 3 5 1	2 3 4 5 1	Меняет третий и второй местами
2 3 4 5 1	2 3 4 5 1	Второй и первый отсортированы, swap не требуется
Четвертый проход (проталкиваем пятый элемент — 1)
2 3 4 5 1	2 3 4 1 5	Меняет пятый и четвертый местами
2 3 4 1 5	2 3 1 4 5	Меняет четвертый и третий местами
2 3 1 4 5	2 1 3 4 5	Меняет третий и второй местами
2 1 3 4 5	1 2 3 4 5	Меняет второй и первый местами. Массив отсортирован.

Оптимизации [ править ]

Бинарные вставки [ править ]

Теперь вместо линейного поиска позиции мы будем использовать бинарный поиск, следовательно количество сравнений изменится с [math]O(N^2)[/math] до [math] O(N\log N) [/math] . Количество сравнений заметно уменьшилось, но для того, чтобы поставить элемент на своё место, всё ещё необходимо переместить большое количество элементов. В итоге время выполнения алгоритма в асимптотически не уменьшилось. Бинарные вставки выгодно использовать только в случае когда сравнение занимает много времени по сравнению со сдвигом. Например когда мы используем массив длинных чисел.

Двухпутевые вставки [ править ]

Суть этого метода в том, что вместо отсортированной части массива мы используем область вывода. Первый элемент помещается в середину области вывода, а место для последующих элементов освобождается путём сдвига элементов влево или вправо туда, куда выгоднее. Пример для набора элементов [math][ 5, 7, 3, 4, 6 ][/math]

До	После	Описание шага
Первый проход (проталкиваем первый элемент — 5)
5	Так как в поле вывода нет элементов, то мы просто добавляем элемент туда.
Второй проход (проталкиваем второй элемент — 7)
5	5 7	С помощью Бинарного поиска находим позицию и, так как позиция крайняя, то сдвигать ничего не приходится.
Третий проход (проталкиваем третий — 3)
5 7	3 5 7	С помощью Бинарного поиска находим позицию и, так как позиция крайняя, то сдвигать ничего не приходится.
Четвертый проход (проталкиваем четвертый элемент — 4)
3 5 7	3 4 5 7	С помощью Бинарного поиска находим позицию. Расстояние до левого края зоны вывода меньше, чем до правого, значит сдвигаем левую часть.
Четвертый проход (проталкиваем пятый элемент — 6)
3 4 5 7	3 4 5 6 7	Расстояние до правого края меньше чем до левого, следовательно двигаем правую часть.

Как можно заметить структура поля вывода имеет сходство с деком, а именно мы выбираем край к которому ближе наш элемент, затем добавляем с этой стороны наш элемент и двигаем его. Как мы видим в этом примере понадобилось сдвинуть всего [math]3[/math] элемента. Благодаря тому что для вставки [math]j[/math] -ого элемента потребуется [math]j/2[/math] сдвигов в худшем случае вместо [math]j[/math] , то и итоговое число необходимых операций в худшем случае составит [math]N^2 / 4 + N \log N[/math] .

Источник

Сортировка вставками

Всем привет. Сегодня продолжаем серию статей, которые я написал специально к запуску курса «Алгоритмы и структуры данных» от OTUS.

Введение

Постановка задачи

Традиционно стоит начать изложение решений задачи с ее постановки. Обычно задача сортировки предполагает упорядочивание некоторого массива целых чисел по возрастанию. Но на самом деле, это является некоторым упрощением. Излагаемые в этом разделе алгоритмы можно применять для упорядочивания массива любых объектов, между которыми установлено отношение порядка (то есть про любые два элемента можно сказать: первый больше второго, второй больше первого или они равны). Упорядочивать можно как по возрастанию, так и по убыванию. Мы же воспользуемся стандартным упрощением.

Сортировка вставками

В прошлый раз мы поговорили об одной из простейших сортировок — сортировке выбором. Сегодня речь пойдет о несколько более сложном алгоритме — сортировке вставками.

Описание алгоритма

Сортировка массива вставками осуществляется так: также как и в случае сортировки выбором массив делится на две части. Одна из частей называется отсортированной, а другая неотсортированной. Алгоритм предполагает проход по всему массиву с тем, чтобы длина отсортированной части стала равна длине всего массива. В рамках каждой итерации мы берем первый элемент неотсортированной части массива и осуществляем с ним следующую операцию: пока наш элемент строго меньше чем предыдущий меняем их местами. После чего увеличиваем длину отсортированной части массива на единицу. Таким образом путем последовательного перемещения изучаемого элемента мы добиваемся того, чтобы он встал на свое место. Пример осуществления одной итерации представлен ниже:
1 3 5 | 2 9 6 -> 1 3 2 5 9 6 -> 1 2 3 5 9 6 -> 1 2 3 5 | 9 6

Реализация

Предлагаю посмотреть на реализацию данного алгоритма на языке C:

Анализ

Предлагаю проанализировать данный алгоритм.

Начать анализ проще всего будет с получения асимптотики памяти. Независимо от длины и структуры предлагаемого для сортировки массива выделяется память только для двух счетчиков цикла и одной вспомогательной переменной, служащей для осуществления обмена двух переменных значениями. Таким образом всегда верно:

Со временем все несколько интереснее. Тело внутреннего цикла само по себе выполняется за O(1), то есть не зависит от размера сортируемого массива. Это означает, что для понимания асимптотики алгоритма необходимо посчитать сколько раз выполняется это тело. Но количество итераций внутреннего цикла зависит от того, насколько хорошо упорядочены (или не упорядочены) элементы сортируемого массива. Для осуществления анализа необходимо посмотреть несколько случаев.

Минимальное количество итераций достигается в том случае, если сортируемый массив уже отсортирован. Действительно, для каждой итерации внешнего цикла for происходит ровно одна итерация внутреннего цикла. Это так называемый лучший случай.

Таким образом, сортировка осуществляется за линейное время.

В худшем случае число итераций предполагается наибольшим, то есть break никогда не срабатывает. На первой итерации внешнего цикла осуществляется одна итерация внутреннего цикла. На второй итерации внешнего цикла осуществляется 2 итерации внутреннего цикла. Продолжая рассуждение дальше, можно прийти к тому, что на последней ((n — 1) — ой) итерации внешнего цикла выполниться (n — 1) итерация внутреннего цикла. Получаем:

Для осуществления вычислений мы воспользовались свойствами О — нотации и формулой суммы арифметической прогрессии.

В среднем случае предполагается, что число итераций внутреннего цикла для какой-то конкретной итерации внешнего цикла равно его среднему значению, то есть математическому ожиданию. Предположим, что все допустимые числа срабатываний внутреннего цикла равновероятны. В таком случае, среднее число итераций внутреннего цикла равно . Предполагается, что i — это номер итерации внешнего цикла. Теперь для подсчета асимптотики необходимо вычислить . То есть мы просто подсчитываем сколько раз выполняется тело внутреннего цикла. Таким образом, получаем .

Если подводить итоги, то асимптотика алгоритма по памяти —

по времени в лучшем случае

и в среднем и в худшем случаях

Поэтому данную сортировку относят к классу квадратичных сортировок.

Также важно заметить, что сортировка выбором в такой реализации является устойчивой. Позволю себе напомнить, что сортировка называется устойчивой, если при ее выполнении порядок следования равных элементов не меняется. Это свойство не очень принципиально для такой учебной задачи, как сортировка массива чисел, но если бы мы сортировали какие-то более сложные объекты с установленным отношением порядка это могло бы быть важно. Подобный пример мы можем рассмотреть как-нибудь в следующий раз, когда будем говорить о поразрядной сортировке.

Источник

В мире алгоритмов: Сортировка Вставками

От автора
Данная статья рассматривает один из алгоритмов сортировки массивов. Она предназначена для новичков или же для тех кто по каким-то причинам не знаком с данным алгоритмом. Исправления и поправки только приветствуются:)

Теория
Сортировка вставками (Insertion Sort) — это простой алгоритм сортировки. Суть его заключается в том что, на каждом шаге алгоритма мы берем один из элементов массива, находим позицию для вставки и вставляем. Стоит отметить что массив из 1-го элемента считается отсортированным.

Словесное описание алгоритма звучит довольно сложно, но на деле это самая простая в реализации сортировка. Каждый из нас, не зависимо от рода деятельности, применял алгоритм сортировки, просто не осознавал это:) Например когда сортировали купюры в кошельке — берем 100 рублей и смотрим — идут 10, 50 и 500 рублёвые купюры. Вот как раз между 50 и 500 и вставляем нашу сотню:) Или приведу пример из всех книжек — игра в карточного «Дурака». Когда мы тянем карту из колоды, смотрим на наши разложенные по возрастанию карты и в зависимости от достоинства вытянутой карты помещаем карту в соответствующее место. Для большей наглядности приведу анимацию из википедии.

Реализация
Прежде чем приступить к реализации определимся с форматом входных данных — для примера это будет массив целочисленных (int) значений. Нумерация элементов массива начинается с 0 и заканчивается n-1. Сам алгоритм реализуем на языке C++. Итак приступим…
Основной цикл алгоритма начинается не с 0-го элемента а с 1-го, потому что элемент до 1-го элемента будет нашей отсортированной последовательностью (помним что массив состоящий из одного элемента является отсортированным) и уже относительно этого элемента с номером 0 мы будем вставлять все остальные. Собственно код:

Реализация сортировки очень проста, всего 3 строчки. Функция swap меняет местами элементы x[j-1] и x[j]. Вложенный цикл ищет место для вставки. Рекомендую запомнить этот алгоритм, чтобы в случае необходимости написать сортировку не позориться сортировкой пузырьком:)

Анализ производительности
Сортировка вставками имеет сложность n 2 , количество сравнений вычисляется по формуле n*(n-1)/2. Для доказательства был написан следующий код:

Количество перестановок для 100 элементов: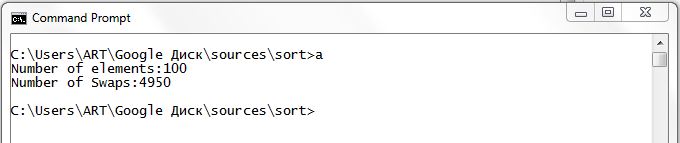

Итак при n=100 количество перестановок равно 4950, а не 10000 если бы мы высчитывали по формуле n 2 . Имейте это ввиду при выборе алгоритма сортировки.

Эффективность
Сортировка вставками наиболее эффективна когда массив уже частично отсортирован и когда элементов массива не много. Если же элементов меньше 10 то данный алгоритм является лучшим. Не зря в быстрой сортировке (оптимизация Боба Седжвика) используется алгоритм сортировки вставками как вспомогательный, но об этом алгоритме мы поговорим позже…

Источник