Способы сортировки элементов массива

Сравнение алгоритмов сортировки

В данной статье рассматриваются алгоритмы сортировки массивов. Для начала представляются выбранные для тестирования алгоритмы с кратким описанием их работы, после чего производится непосредственно тестирование, результаты которого заносятся в таблицу и производятся окончательные выводы.

Алгоритмы сортировок очень широко применяются в программировании, но иногда программисты даже не задумываются какой алгоритм работает лучше всех (под понятием «лучше всех» имеется ввиду сочетание быстродействия и сложности как написания, так и выполнения).

В данной статье постараемся это выяснить. Для обеспечения наилучших результатов все представленные алгоритмы будут сортировать целочисленный массив из 200 элементов. Компьютер, на котором будет проводится тестирование имеет следующие характеристики: процессор AMD A6-3400M 4×1.4 GHz, оперативная память 8 GB, операционная система Windows 10 x64 build 10586.36.

Для проведения исследования были выбраны следующие алгоритмы сортировки:

Selection sort (сортировка выбором) – суть алгоритма заключается в проходе по массиву от начала до конца в поиске минимального элемента массива и перемещении его в начало. Сложность такого алгоритма O(n2).

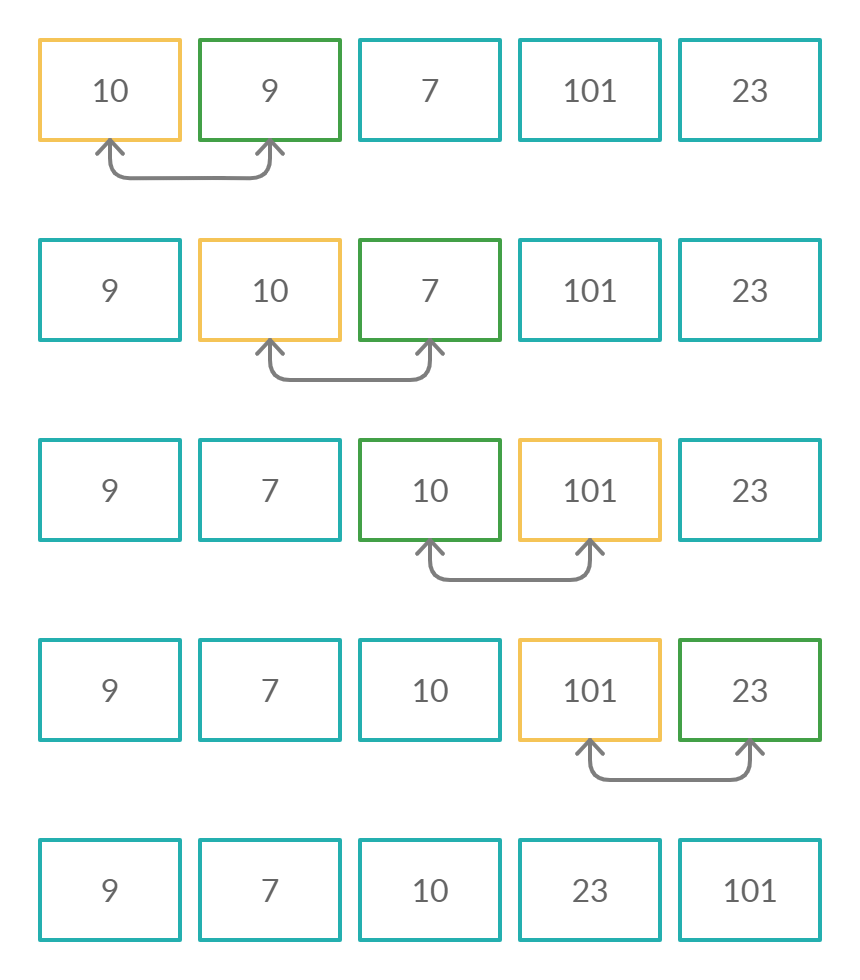
Bubble sort (сортировка пузырьком) – данный алгоритм меняет местами два соседних элемента, если первый элемент массива больше второго. Так происходит до тех пор, пока алгоритм не обменяет местами все неотсортированные элементы. Сложность данного алгоритма сортировки равна O(n^2).

Insertion sort (сортировка вставками) – алгоритм сортирует массив по мере прохождения по его элементам. На каждой итерации берется элемент и сравнивается с каждым элементом в уже отсортированной части массива, таким образом находя «свое место», после чего элемент вставляется на свою позицию. Так происходит до тех пор, пока алгоритм не пройдет по всему массиву. На выходе получим отсортированный массив. Сложность данного алгоритма равна O(n^2).

Quick sort (быстрая сортировка) – суть алгоритма заключается в разделении массива на два под-массива, средней линией считается элемент, который находится в самом центре массива. В ходе работы алгоритма элементы, меньшие чем средний будут перемещены в лево, а большие в право. Такое же действие будет происходить рекурсивно и с под-массива, они будут разделяться на еще два под-массива до тех пор, пока не будет чего разделать (останется один элемент). На выходе получим отсортированный массив. Сложность алгоритма зависит от входных данных и в лучшем случае будет равняться O(n×2log2n). В худшем случае O(n^2). Существует также среднее значение, это O(n×log2n).

Comb sort (сортировка расческой) – идея работы алгоритма крайне похожа на сортировку обменом, но главным отличием является то, что сравниваются не два соседних элемента, а элементы на промежутке, к примеру, в пять элементов. Это обеспечивает от избавления мелких значений в конце, что способствует ускорению сортировки в крупных массивах. Первая итерация совершается с шагом, рассчитанным по формуле (размер массива)/(фактор уменьшения), где фактор уменьшения равен приблизительно 1,247330950103979, или округлено до 1,3. Вторая и последующие итерации будут проходить с шагом (текущий шаг)/(фактор уменьшения) и будут происходить до тех пор, пока шаг не будет равен единице. Практически в любом случае сложность алгоритма равняется O(n×log2n).

Для проведения тестирования будет произведено по 5 запусков каждого алгоритма и выбрано наилучшее время. Наилучшее время и используемая при этом память будут занесены в таблицу. Также будет проведено тестирование скорости сортировки массива размером в 10, 50, 200 и 1000 элементов чтобы определить для каких задач предназначен конкретный алгоритм.

Полностью неотсортированный массив:

Частично отсортированный массив (половина элементов упорядочена):

Результаты, предоставленые в графиках:

В результате проведенного исследования и полученных данных, для сортировки неотсортированного массива, наиболее оптимальным из представленных алгоритмов для сортировки массива является быстрая сортировка. Несмотря на более длительное время выполнения алгоритм потребляет меньше памяти, что может быть важным в крупных проектах. Однако такие алгоритмы как сортировка выбором, обменом и вставками могут лучше подойти для научных целей, например, в обучении, где не нужно обрабатывать огромное количество данных. При частично отсортированном массиве результаты не сильно отличаются, все алгоритмы сортировки показывают время примерно на 2-3 миллисекунды меньше. Однако при сортировке частично отсортированного массива быстрая сортировка срабатывает намного быстрее и потребляет меньшее количество памяти.

Источник

Алгоритмы сортировки

Алгоритм сортировки — это алгоритм для упорядочивания элементов в списке.

Виды алгоритмов сортировки

Сортировка пузырьком / Bubble sort

Сортировка пузырьком — это простейший и один из самых известных алгоритмов сортировки. Идея заключается в последовательном сравнении значений соседних элементов. Если текущий элемент больше следующего, меняем их местами. Алгоритм необходимо повторять до тех пор, пока массив не будет отсортирован.

Плюсы и минусы

Этот алгоритм считается учебным и почти не применяется на практике из-за низкой эффективности: он медленно работает на тестах, в которых маленькие элементы (их называют «черепахами») стоят в конце массива. Однако на нём основаны многие другие методы, например, шейкерная сортировка и сортировка расчёской.

Пример реализации на Kotlin:

Сложность	Лучшее	Среднее	Худшее
Время	O(n)	O(n 2 )	O(n 2 )
Память			O(1)

Сортировка перемешиванием / Shaker (cocktail, ripple, shuffle, shuttle) sort

Также известна как шейкерная или коктейльная сортировка.

Сортировка перемешиванием — это разновидность сортировки пузырьком. Отличие в том, что данная сортировка в рамках одной итерации проходит по массиву в обоих направлениях (слева направо и справа налево), тогда как сортировка пузырьком — только в одном направлении (слева направо).

Общая идея алгоритма:

• Обход массива слева направо, аналогично пузырьковой — сравнение соседних элементов, меняя их местами, если левое значение больше правого. В итоге наибольшее число будет перемещено в конец массива.
• Обход массива в обратном направлении (справа налево), начиная с элемента, который находится перед последним отсортированным. На этом этапе элементы также сравниваются между собой и меняются местами, чтобы наименьшее значение всегда было слева. В итоге наименьшее число будет перемещено в начало массива.

Пример реализации на Kotlin:

Сложность	Лучшее	Среднее	Худшее
Время	O(n)	O(n 2 )	O(n 2 )
Память			O(1)

Сложность у алгоритма такая же, как и у сортировки пузырьком, однако реальное время работы лучше (обычно менее чем в два раза быстрее).

Сортировка расчёской / Comb sort

Сортировка расчёской — еще одна разновидность сортировки пузырьком. Данная сортировка улучшает сортировку пузырьком за счет устранения маленьких значений в конце списка (черепах).

Достигается это тем, что вместо сравнения соседних элементов, сравниваются элементы на достаточно большом расстоянии друг от друга, постепенно уменьшая это расстояние. Сначала разрыв между элементами берётся максимальный, т.е. на единицу меньше, чем размер массива. Затем на каждой итерации расстояние уменьшается путём деления расстояния на фактор уменьшения. Так продолжается до тех пор, пока разность индексов сравниваемых элементов не достигнет единицы. Тогда сравниваются уже соседние элементы как и в сортировке пузырьком, но эта итерация будет последней.

Оптимальное значение фактора уменьшения — 1,247.

Пример реализации на Kotlin:

Сложность	Лучшее	Среднее	Худшее
Время	O(n log n)	Ω(n 2 /2 p ), где p — количество инкрементов	O(n 2 )
Память			O(1)

Сортировка вставками / Insertion sort

Сортировка вставками — алгоритм, при котором каждый последующий элемент массива сравнивается с предыдущими элементами (отсортированными) и вставляется в нужную позицию.

Общая идея алгоритма:

• Сравниваем второй элемент с первым элементом массива и при необходимости меняем их местами. Условно эти элементы (первый и второй) будут являться отсортированным массивом, остальные элементы — неотсортированным.
• Сравниваем следующий элемент из неотсортированного массива с элементами отсортированного и вставляем в нужную позицию.
• Повторям шаг 2 до тех пор, пока в неотсортированном массиве не останется элементов.

Пример реализации на Kotlin:

Сложность	Лучшее	Среднее	Худшее
Время	O(n)	O(n 2 )	O(n 2 )
Память			O(1)

Сортировка Шелла / Shell sort

Сортировка Шелла — усовершенствованная разновидность сортировки вставками.

Сначала сравниваются и сортируются между собой значения, стоящие друг от друга на некотором расстоянии — d. После этого расстояние d уменьшается и процедура повторяется до тех пор, пока значение d не станет минимальным, т.е. d = 1. Это означает, что сортировка достигла последнего шага. А на последнем шага элементы сортируются обычной сортировкой вставками.

Первоначально было предложено расчитывать расстояние между сравниваемыми элементами следующим образом:

• первая итерация — d₁ = N/2, где N — размер массива;
• последующие итерации — d_i = d_i-1/2;
• последняя итерация — d_k = 1

Существуют и другие последовательности.

Пример реализации на Kotlin:

Сложность	Лучшее	Среднее	Худшее
Время	O(n log n)	зависит от выбранных шагов (d)	O(n 2 ) или O(n log 2 n) (зависит от выбранных шагов)
Память			O(1)

Сортировка выбором / Selection Sort

Сортировка выбором — это алгоритм, при котором многократно осуществляется поиск минимального элемента в неотсортированной части массива и его помещение в конец отсортированной части массива.

Общая идея алгоритма:

• Данный алгоритм условно делит массив на две части:
  • подмассив, который уже отсортирован (находится в левой части массива),
  • подмассив, который нужно отсортировать (находится в правой части массива).
• Поиск минимального значения в неотсортированном массиве. Найденное значение меняем местами с первым элементом в неотсортированном массиве.
• Повторяем предыдущий шаг до тех пор, пока массив не будет отсортирован.

Пример реализации на Kotlin:

Сложность	Лучшее	Среднее	Худшее
Время	O(n 2 )	O(n 2 )	O(n 2 )
Память			O(1)

Быстрая сортировка / Quick Sort

Быстрая сортировка — это алгоритм типа “разделяй и властвуй”.

Общая идея алгоритма:

• Выбрать из массива элемент, который обычно называют опорным. Это может быть любой элемент из массива. От выбора опорного элемента не зависит корректность алгоритма, но в отдельных случаях может сильно зависеть его эффективность.
• Сравнить все остальные элементы с опорным и переставить их в массиве так, чтобы разбить массив на три непрерывных отрезка, следующих друг за другом: «элементы меньшие опорного», «равные» и «большие».
• Рекурсивно применить первые два шага к отрезкам, содержащим «меньшие» и «большие» значения. Не применять к массиву, в котором только один элемент или отсутствуют элементы.

Пример реализации на Kotlin:

Сложность	Лучшее	Среднее	Худшее
Время	O(n)	O(n log n)	O(n 2 )
Память			O(n)

Сортировка слиянием / Merge sort

Сортировка слиянием — это алгоритм типа “разделяй и властвуй”.

Общая идея алгоритма:

• Массив разбивается на две части примерно одинакового размера. Разбиение получившихся массивов повторяется до тех пор, пока размер каждого массива не достигнет единицы.
• Каждая из получившихся частей сортируется отдельно, после чего происходит слияние двух массивов следующим образом:
  • На каждом шаге сравниваем первые элементы массивов, берём наименьшее значение и записываем в результирующий массив.
  • Когда один из массив закончился, добавляем оставшиеся элементы второго массива в результирующий массив.
• Слияние подмассивов продолжается до тех пор, пока не получим один, отсортированный массив.

Пример реализации на Kotlin:

Сложность	Лучшее	Среднее	Худшее
Время	O(n log n)	O(n log n)	O(n log n)
Память			O(n)

Пирамидальная сортировка / Heap sort

Пирамидальная сортировка — это улучшенная сортировка выбором.

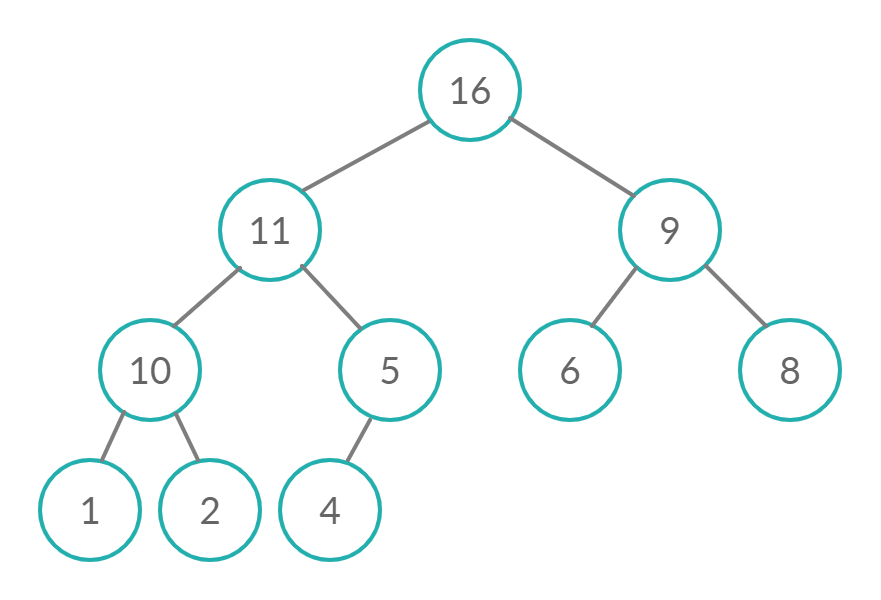
Для сортировки используется бинарное сортирующее дерево — дерево, у которого выполнены условия:

• Каждый лист имеет глубину либо d, либо d-1, d — максимальная глубина дерева.
• Значение в любой вершине не меньше значения её потомков.

Общая идея алгоритма:

Выстраиваем массив в виде сортирующего дерева:
Array[i] >= Array[2i + 1]
Array[i] >= Array[2i + 2]
при 0

Сложность	Лучшее	Среднее	Худшее
Время	O(n log n)	O(n log n)	O(n log n) или O(n) (при одинаковых ключах)
Память			O(1)

Сортировка подсчётом / Counting sort

Сортировка подсчётом — это алгоритм, основанный на подсчёте повторяющихся элементов в массиве.

Общая идея алгоритма (простой вариант):

• Есть массив A длиной n элементов, который нужно отсортировать. Создаётся вспомогательный массив C с индексами от 0 до k (максимальное значение в массиве A) и заполняется нулями.
• Последовательно проходим по массиву A и записываем в C[i] количество чисел, равных i. Таким образом индексы в массиве C — это значения массива A, а значение в массиве C — это то, сколько раз это число повторяется в массиве A.
• Проходим по массиву C и переносим значения в массив A.

Пример реализации на Kotlin:

Сложность	Лучшее	Среднее	Худшее
Время	Ω(n+k)	θ(n+k)	O(n + k)
Память			O(k)

• n — размер отсортированного массива, а k — размер вспомогательного массива

Блочная (карманная, корзинная) сортировка / Bucket sort

Блочная сортировка — это алгоритм, основанный на разделении входного массива на несколько частей — блоки/сегменты — и использовании другого алгоритма для их сортировки.

Общая идея алгоритма:

• Делим массив на блоки таким образом, чтобы элементы в каждом следующем блоке были всегда больше, чем в предыдущем.
• Сортируем каждый блок, используя какой-либо другой алгоритм сортировки, либо рекурсивно тем же методом разбиения на блоки.
• Объединяем все блоки в один массив.

Пример реализации на Kotlin:

Сложность	Лучшее	Среднее	Худшее
Время	Ω(n+k)	θ(n+k)	O(n 2 )
Память			O(1)

Поразрядная (цифровая) сортировка / Radix sort

Поразрядная сортировка — это алгоритм, который использует внутреннюю структуру сортируемых объектов.

Перед началом сортировки необходимо знать:

• length — максимальное количество разрядов в сортируемых величинах (например, при сортировке слов необходимо знать максимальное количество букв в слове);
• rang количество возможных значений одного разряда (при сортировке слов – количество букв в алфавите).

Общая идея алгоритма:

• Создаём пустые массивы, количество которых равно rang.
• Распределяем исходные значения по этим массивам. Распределение осуществляется по значению младшего (крайнего) разряда.
• Соединяем значения в той последовательности, в которой они находятся после распределения по спискам.
• Повторяем шаги 1-2 для оставшихся разрядов.

Пример реализации на Kotlin:

Сложность	Лучшее	Среднее	Худшее
Время	Ω(n+w)	θ(nk)	O(w * n)
Память			O(n + w)

• w — количество бит, требуемых для хранения каждого ключа.

Битонная сортировка / Bitonic sort

Битонная сортировка — алгоритм, основанный на понятии битонных последовательностей и операций над ними.

Битонная последовательность — последовательность, которая сначала возрастает, а потом убывает.

Общая идея алгоритма:

• Создаём битонную последовательность. В результате получаем два массива: первый отсортирован в порядке возрастания, второй — в порядке убывания.
• Последовательно сравниваем элементы первого и второго массивов (сначала первые элементы, потом вторые и т.д.). Если какой либо элемент из второго массива окажется меньше, то меняем его местами с элементом из первого массива. В результате в первом массиве окажутся наименьшие элементы из обоих массивов, а во втором — наибольшие. При этом каждый из массивов будет являться битонной последовательностью.
• Рекурсивно применяем второй шаг к отсортированным массивам, после чего массивы можно склеить.



Чтобы превратить произвольную последовательность в битонную, нужно:

• разделить последовательность пополам;
• первую часть отсортировать по возрастанию;
• вторую часть отсортировать по убыванию.

Пример реализации на Kotlin:

Сложность	Лучшее	Среднее	Худшее
Время	O(log 2 (n)	O(log 2 (n)	O(log 2 (n)
Память			O(log 2 (n)

Timsort

Timsort — гибридный алгоритм, сочетающий в себе сортировку вставками и сортировку слиянием.

Общая идея алгоритма:

• По специальному алгоритму разделяем входной массив на подмассивы.
• Каждый подмассив сортируем при помощи сортировки вставками.
• Отсортированные массивы собираются в единый массив с помощью модифицированной сортировки слиянием.

Пример реализации на Kotlin:

Источник

Читайте также:  Легкий способ бросить есть сладкое