Способы соединения обмоток генератора с нагрузкой

3.3 Основные схемы соединения трехфазного генератора и нагрузки

Если к каждой фазе генератора при помощи двух проводов присоединить нагрузочные сопротивления, то образуется три электрически не связанные цепи однофазного синусоидального тока.

За положительные направления в трехфазных цепях принимают:

• для ЭДС – от концов фаз к началам;
• для токов – от генератора к нагрузке.

Несвязанные трехфазные цепи не нашли применения из-за их неэкономичности (большое число проводов). Практически в реальных трехфазных системах цепи отдельных фаз объединяются в общую систему по схеме «звезда» или «треугольник». При этом число соединительных проводов уменьшается до трех, четырех и возможны пять простейших способов соединения трехфазного генератора и нагрузки: звезда – звезда; звезда – звезда с нейтральным проводом; звезда – треугольник; треугольник – звезда; треугольник – треугольник.

3.3.1 Соединение по схеме звезда

3.3.2 Соединение трехфазного генератора и нагрузки по схеме треугольник

3.3.1 Соединение по схеме звезда

При соединении фаз генератора или обмоток трехфазного трансформатора в звезду их концы x,y,z соединяют в одну общую точку N, называемую нулевой или нейтральной. Начала фаз выводят на клеммную колодку, куда подключают провода, соединяющие генератор с приемником. Эти провода образуют трехфазную линию и называются линейными (рис.3.4).

Рисунок 3.4 – Соединение трехфазного генератора и нагрузки по схеме звезда

Если нейтральная точка генератора соединена с нейтральной точкой нагрузки, то образуется четырехпроводная трехфазная цепь. Провод, соединяющий нейтральные точки генератора и нагрузки называется нулевым или нейтральным.

Токи, текущие по линейным проводам, называют линейными токами и обозначают I_А;I_B;I_C — I_Л

Напряжения между линейными проводами называют линейными напряжениями и обозначают U_АB;U_BC;U_CA — U_Л.

Нагрузка, как и фазы генератора, может быть соединена в звезду. При этом каждое из трех сопротивлений нагрузки z_А;z_B;z_C называется фазой нагрузки. Токи, текущие по фазам нагрузки, называют фазовыми токами I_А;I_B;I_C — I_Ф, а напряжения на фазах нагрузки – фазовыми напряжениями U_А;U_B;U_C — U_Ф.

При соединении генератора в звезду:

а) линейные напряжения по модулю в √3 больше фазовых напряжений генератора:

б) линейный ток генератора равен его фазовому току:

При соединении нагрузки в звезду:

а) линейный ток равен фазовому:

б) линейные напряжения связаны с фазовыми соотношениями:

В симметричной трехфазной системе . Тогда

Если нагрузочные сопротивления одинаковы по величине и характеру, то такая нагрузка называется равномерной.

При равномерной нагрузке:

и нейтральный провод можно изъять без изменения режима работы цепи.

Векторная диаграмма при индуктивном характере равномерной нагрузки показана на рисунке 3.5.

Рисунок 3.5 – Векторная диаграмма при индуктивном характере равномерной нагрузки

3.3.2 Соединение трехфазного генератора и нагрузки по схеме треугольник

Чтобы соединить фазы трехфазного генератора (или трансформатора) в треугольник, нужно конец каждой фазы подключить к началу следующей (рис.3.6). При таком соединении симметричного генератора с отключенной нагрузкой внутри него никаких токов нет, так как

Рисунок 3.6 – Соединение трехфазного генератора и нагрузки по схеме треугольник

При соединении по схеме «треугольник – треугольник» фазовые напряжения генератора и приемника одновременно являются линейными, т.е.

Линейные и фазовые токи отличаются. Для получения соотношений между ними следует единообразно выбрать их направления:

а) для линейных токов – от генератра к нагрузке;

б) для фазовых – по часовой стрелке.

Из этих соотношений видно, что при равномерной нагрузке

При равномерной нагрузке линейный ток по модулю в √3 больше фазового.

Векторная диаграмма при индуктивном характере равномерной нагрузки показана на рисунке 3.7.

Рисунок 3.7 – Векторная диаграмма при индуктивном характере равномерной нагрузки

Источник

Соединение обмоток генератора «звездой » и «треугольником»

Вы будете перенаправлены на Автор24

Пусть, мы имеем генератор переменного тока с тремя отдельными обмотками, расположенными под углом $120^0$ относительно друг друга. В этих обмотках создается трехфазный ток. Напряжения на обмотках равно:

В том случае, если данный генератор использовать без связи друг с другом, то генератор трехфазного тока становится просто совокупностью отдельных генераторов однофазного тока. В том случае, если обмотки соединяются определенным способом, то у трехфазного тока возникают специальные свойства, которые используют в технике. Используют два вида соединений обмоток генератора: «звездой» и «треугольником».

Соединение «звезда»

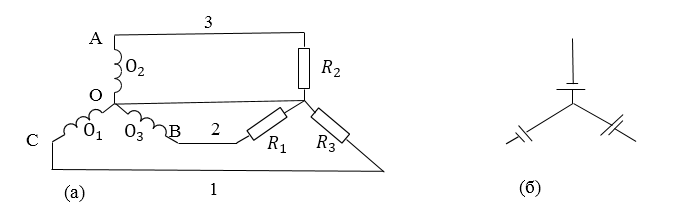
Рассмотрим схему соединения обмоток генератора «звездой». В ней концы трех обмоток соединяют в один узел, а начала служат для подключения нагрузок.

Схема соединения звездой показана на рис.1 (а). Такое соединение обмоток генератора позволяет использовать для передачи электроэнергии вместо шести проводов только четыре. Точка $O$ на схеме — точка общего потенциала (проводник, который соединен с точкой $О$ — нулевой провод). Такое соединение подобно соединению трех источников тока, которое показано на рис.1 (б).

При таком способе соединения напряжение между фазой и нулевым проводом называют фазным напряжением. Напряжение между фазами $A-B$, $B-C$, $C-A$ называют линейным. Для того, чтобы определить как соотносятся фазное и линейное напряжения необходимо брать геометрическую (векторную) разность.

Допустим, что генератор разомкнут, то есть $R_1=\ R_2=R_3=\infty ,\ $найдем связь между фазным напряжением (существующим в каждой из обмоток $О_1,\ О_2,О_3$) и линейными напряжениями (между проводами $0,1,2,3$). Линейное напряжение между проводом $О$ и любым другим проводом равно фазному и его амплитуда $U_m.\ $Линейное напряжение между любой парой проводов $1,2$ и $3$ будет отличаться. Найдем напряжение между проводами $1$ и $3$, которое равно разности потенциалов между свободными концами обмоток $О_1,\ О_2$:

Готовые работы на аналогичную тему

Из формулы (2) видно, что линейное напряжение имеет такую же частоту, что и фазное. Однако, амплитуда линейного напряжения в $\sqrt<3>$ больше, чем фазного.

Допустим, что генератор имеет симметричную нагрузку ($R_1=\ R_2=R_3$). В таком случае амплитуда токов в проводах $1,2,3$ одинакова ($I_m$). Сила тока будет изменяться в соответствии с:

В нулевом проводе сила тока ($I$) равна сумме линейных токов:

Мы получили, что при симметричной нагрузке сила тока в нулевом проводе всегда равна нулю. В таком случае (при симметричной нагрузке!) нулевой провод можно удалить совсем и линия будет работать (однако, надо помнить, что при этом на каждую из пар нагрузок будет действовать линейное напряжение в $\sqrt<3>$ раз больше фазного).

Соединение треугольник

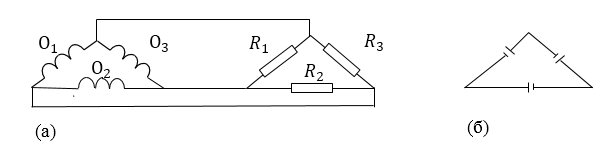
Обмотки трехфазного генератора и трехфазные нагрузки могут соединяться еще одним способом. В этом случае конец первой обмотки соединяется с началом второй, конец второй — с началом третьей, конец третьей с началом первой. При этом узлы соединений служат отводами. Такой способ соединения называют треугольником.

Схема соединения треугольник изображена на рис.2(а). Для основной гармоники при соединении обмоток генератора по схеме треугольник ток замыкания в обмотке равен нулю. Обмотки мощных генераторов обычно по такой схеме не соединяют. Эта схема соответствует соединению источников напряжения, которая изображена на рис. 2 (б).

Если бы ток был постоянным, то все обмотки при таком соединении были бы замкнуты накоротко. Но, если мы имеем дело с переменными напряжениями, которые имеют разность фаз, то дело коренным образом изменяется. Результирующее напряжение в треугольнике (см. схему вычисления (4)) равно:

Мы получаем, что если генератор не имеет нагрузки, то в обмотках нет тока. Из рис. 2 очевидно, что линейные напряжения равны фазным напряжениям. При разомкнутом генераторе амплитуда линейных напряжений равна амплитуде напряжения в одной обмотке $U_m.$

В соединении треугольником нет нулевого провода, неравномерность нагрузки существеннее сказывается на работе генератора, чем в случае соединения звездой. Из-за этой особенности соединение треугольник чаще всего применяют в силовых установках, например, трехфазных двигателях, где можно получить близкие по величине нагрузки фаз.

Предполагалось, что генератор и нагрузки соединялись одинаково (звездой или треугольником), конечно, возможны комбинации схем. Например, потребитель соединяется звездой, генератор треугольником.

Задание: Объясните, что произойдет в схеме, которая изображена на рис.1 (а), если оборван провод $1$? Что случится, если перегорел нулевой провод?

Решение:

Допустим, что в схеме соединения звезда (рис.1(а)) оборван провод $1$. Тогда нагрузка $R_1$ , будет выключена. Нагрузки $R_2\ и\ R_3$ будут нормально работать, так как на них будут присутствовать фазные напряжения.

Пусть перегорел нулевой провод. В этом случае каждая пара сопротивлений, например $R_1\ и\ R_2$ будут соединены последовательно и попадут под напряжение в $\sqrt<3>$ раз больше фазного. Это напряжение распределится в соответствии с правилами последовательного соединения, пропорционально сопротивлениям (в данном случае $R_1\ и\ R_2$). Так, если $R_1=R,\ R_2=\frac<1><10>R$, то на ветке $R_2$ мы получим $0,1U$, а на ветке $R_1$ будет $0,9 U$, где $U$- полное напряжение. Допустим, что напряжение в сети (фазное) $220В$, тогда:

\[U=\sqrt<3>\cdot 220=380\ \left(B\right)\left(1.1\right).\]

Из $380В$ на сопротивление $R_1$ придется $342 В$, тогда как на $R_2$ придется $38В$. Поэтому, если в качестве $R_1$ будет, например бытовая лампочка, она перегорит и ток в обеих ветвях прервётся.

Задание: Объясните, почему соединение звездой применяют в технике освещения?

Решение:

Необходимость применения соединения «звезда», которая имеет нулевой провод, существует в технике освещения, так как при работе осветительных приборов невозможно добиться симметрии в нагрузках. В таких сетях все три фазы и нулевой (нейтральный) провод подводят, например, к жилым домам, внутри дома пытаются примерно одинаково нагрузить каждую фазу, так чтобы общая нагрузка была наиболее симметричной. При этом к каждой квартире приходит нулевой провод и одна из фаз. На распределительный щит, через который проходят две или три фазы, в нулевой провод предохранитель не ставят, так как его перегорание ведет асимметрии напряжений.

Источник

Варианты подключения обмоток трехфазных генераторов

При работе 3-х фазного генератора в каждой его обмотке создается ЭДС в форме синусоидального колебания. Все вектора разнесены по углу вращения на 120° и могут быть описаны формулами:

Для подключения обмоток генератора в связанную систему применяется одна из двух схем:

— “звезда” (Y); — “треугольник” (Δ).

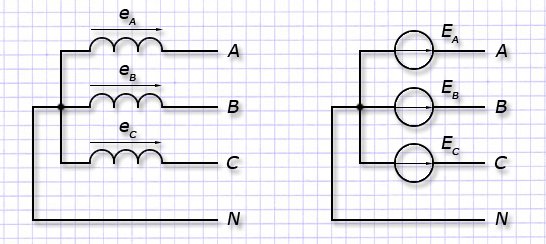
“Звезда”. Для схемы “звезды” все выходы обмоток фаз статора подключают к единой общей точке N, именуемую нейтральной либо нулевой точкой. Входа (начала) обмоток каждой фазы А, В и С подключают к линейным выводам генератора.

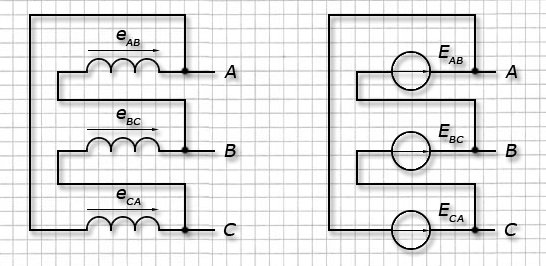
“Треугольник”. Для этой схемы соединения формируют выходные фазы:

— “А” подключением выхода обмотки А ко входу обмотки C; — “В” подключением выхода обмотки В ко входу обмотки А; — “С” подключением выхода обмотки С ко входу обмотки В.

Точки подключения А, В и С используются как линейные выводы у генератора.

Векторные диаграммы. У работающего генератора, обмотки которого соединены по схеме “звезда” диаграмма векторов напряжений имеет форму равностороннего треугольника с центром в начале координат и расположенного симметрично относительно оси ординат.

Его стороны представлены векторами линейных напряжений с направлением вращения противоположным ходу часовой стрелки. Вектора фазных напряжений соединяют центр треугольника с вершинами по направлению от начала координат.

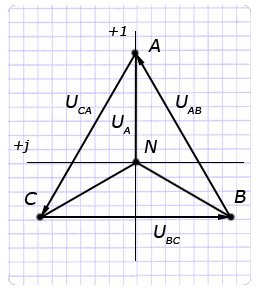
Под термином фазного напряжения понимают разность потенциалов между общим выводом N и линейным А, В или С и маркируют: U_A, U_B, U_C. Напряжения в фазах генератора равны ЭДС обмоток: Е_А=U_А, Е_В=U_В, Е_С=U_С.

Линейное напряжение генератора измеряется между двумя любыми его выводами и обозначается по наименованию выбранных фаз: U_AВ, U_BС, U_CА. Величина вектора линейного напряжения определяется геометрической разностью векторов соответствующих фаз:

У генератора с обмотками соединенными по схеме “треугольник” диаграмма векторов напряжений тоже имеет форму равностороннего треугольника, но он относительно центра координат провернут на 30° по направлению движения часовой стрелки.

Соотношения линейных и фазных напряжений для генератора, собранного по схеме “треугольника”, остаются теми же, что и для генератора, работающего по схеме “звезда”.

Расчеты параметров трехфазных сетей проводятся математическими способами (например, комплексный метод) и способами геометрических сложений.

Для этого выбирают один из векторов в качестве начального, ориентируют его в комплексной плоскости с учетом направления и величины. Остальные вектора достраивают по углам сдвига их фаз относительно выбранного начального вектора с учетом их величин.

Обычные расчеты для схемы соединения “звезда” проще начинать с определения напряжения вектора фазы А, который в данной системе выходит из начала координат комплексной плоскости в направлении на север. Выражения фазных напряжений в комплексной форме для такого расчета описываются формулами:

Формулы для линейных векторов имеют следующий вид:

Для схем “треугольник” за начальный отсчет принимают вектор линейного напряжения U_АВ. Формулы вычисления фазных векторов напряжений принимают выражения:

Вектора линейных напряжений описываются формулами:

Проведя геометрические вычисления не сложно определить линейную величину вектора по значению фазной:

Важно! Схема соединения обмоток “треугольник” для генератора практически не пригодна для реального использования, поэтому ее запрещено применять.

В фазах схемы “треугольник” образуется общий контур, у которого возникает суммарная ЭДС Σe=e_AB+e_BC+e_CA. Значения полных сопротивлений в обмотках маленькие и даже небольшая величина суммарной ЭДС Σe>0 вызывает в магистралях “треугольника” уравнительные токи, которые сопоставимы с номинальным значением тока в генераторе. Это создает большие потери энергии и значительно уменьшает КПД генератора.

У энергетиков существует определение номинального напряжения для 3-х фазной системы. Им называют линейные напряжения, которые выражаются в киловольтах (кВ, kV). Их представляют значениями 0,4; 1,1; 3,5; 6,3; 10,5; 22; 35; 63; 110; 220; 330; 500; 750.

Для потребителей электроэнергии номинальную величину 3-х фазного напряжения допускается указывать соотношениями линейных и фазных напряжений U_Л/U_Ф. Для электросети 0,4 кВ оно будет иметь вид: 380/220 вольт.

Источник