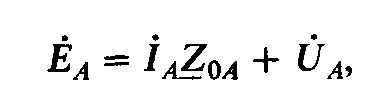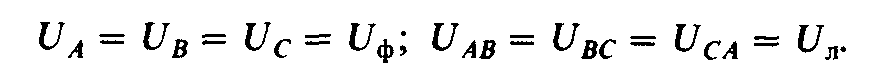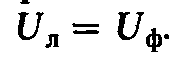Способы соединения фаз трехфазного источника питания

4.2. Способы соединения фаз источника трехфазного тока и соотношения между его линейными и фазными напряжениями

На рис. 4.4 показана схема трехфазной цепи, фазы которой электри­чески не связаны друг с другом. Такую трехфазную цепь называют несвязанной. Так как в несвязанной трехфазной цепи каждая из фаз источника соединяется с приемником двумя проводами, то в этом слу­чае имеется шесть соединительных проводов. Несвязанные трехфазные цепи неэкономичны, и обычно их не применяют.

С целью уменьшения числа соединительных проводов в трех­фазной системе используют связанные цепи, в которых фазы источника (или приемника) соединяются между собой звездой или треугольником. Трехфазная система создана и внедрена в практику русским уче­ным М. О. Доливо-Добровольским в 90-х годах XIX столетия, кото­рый изобрел все звенья этой системы — генераторы, трансформаторы, линии электропередачи и двигатели трехфазного тока.

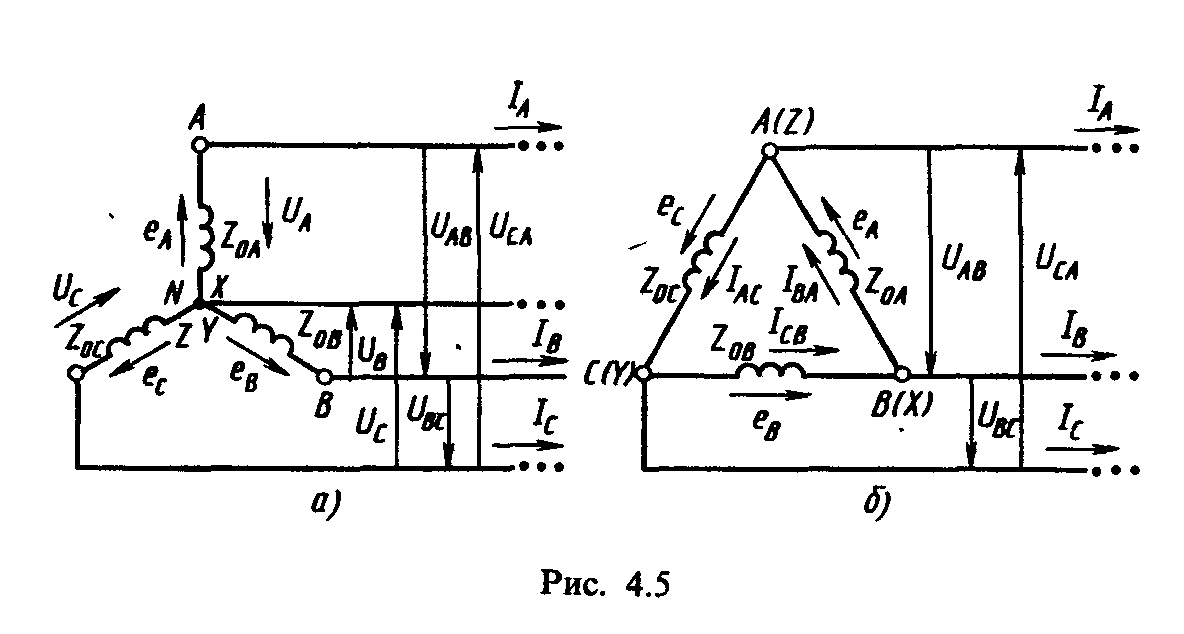
При соединении фаз источника звездой (рис. 4.5, а) концы фаз X, Y, Z объединены в общую точку N, называемую нейтральной, а начала фаз А, В, С с помощью проводов соединены с приемником тремя проводами, которые называются линейными. Такую трехфазную систему называют трехпроводной.

При соединении фаз источника треугольником (рис. 4.5, б) необ­ходимо подключить конец каждой фазы к началу следующей, т. е. конец X первой фазы — с началом В второй фазы, конец Y второй фазы—с началом С третьей фазы и конец Z третьей фазы — с началом А первой фазы. Начала фаз А, В, С с помощью проводов соединяют с приемниками. Следует отметить, что при соединении треугольником фазы источника создают замкнутый контур и на первый взгляд может показаться, что в контуре при отключенных приемниках может воз­никнуть ток короткого замыкания, однако этого не происходит, так как в симметричной трехфазной системе сумма мгновенных значений э. д. с. 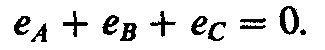Следовательно, при холостом ходе источника ток в его фазах не возникает.

Соединение отдельных фаз трехфазных приемников звездой или треугольником осуществляют таким же образом, как и соединение звездой или треугольником ис­точников. При соединении ис­точника, например, звездой при­емники могут быть соединены различным способом, т. е. од­ни — звездой, а другие — тре­угольником и т. д. Если нагрузка несимметричная, т. е. сопротив­ления фаз приемника не равны между собой, то при соединении источника и приемников звездой необходимо применять помимо трех линейных проводов четвертый, нейтральный про-

в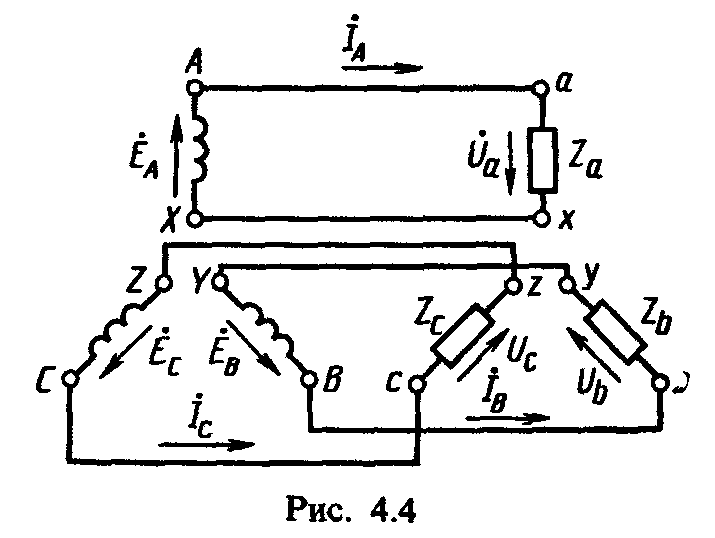од, соединяю­щий нейтральные точки N и N’ источника и приемника (далее рис. 4.7, а).

Напряжение между началом и концом фазы источника называют фазным (U_ф). Например, при соединении звездой фазными являются напряжения между началами фаз и нейтральной точкой источника N (рис. 4.5, а).

Фазными токами (I_ф) называются токи, проходящие через каждую фазу источника или приемника. Напряжения между началами А, В, С фаз источника или между линейными проводами называются линейными напряжениями U_л, а токи в линейных проводах — линейными токами I_л.

При анализе трехфазных цепей важно знать условные положитель­ные направления э. д. с., напряжений и токов, ибо от их выбора зависят знаки в уравнениях, составляемых по законам Кирхгофа, а также направ­ления векторов на векторных диаграммах. Как уже указывалось (см. п. 4.1), за условное положительное направление э. д. с. в каждой фазе источника принимают направление от ее конца к началу, а за условное положительное направление напряжения в каждой фазе источника принимают направление от начала фазы к ее концу, направление же фазных токов совпадает с направлением э. д. с. в каждой фазе источника (рис. 4.5, а, б).

За условные положительные направления линейных напряжений принимают направление от начала одной фазы к началу другой, в частности напряжение U_AB направлено от А к В, напряжение U_BC — от В к С, напряжение V_CA — от С к А. Линейные токи, проходящие через линейные провода, всегда направлены от источника к приемнику (рис. 4.5, а, 6). Фазные напряжения и токи приемников направлены в одну и ту же сторону.

Согласно второму закону Кирхгофа, э. д. с. фазы АХ при соединении звездой (рис. 4,5, а)

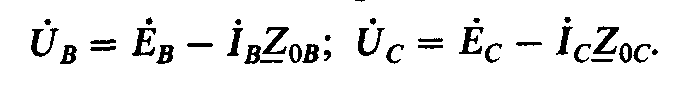
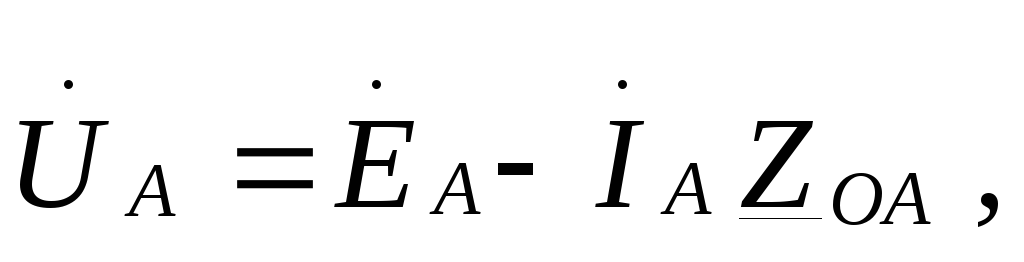
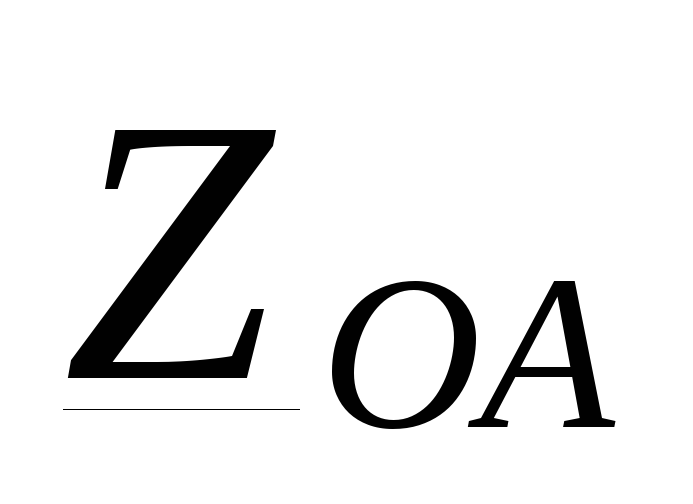
откудагде— внутреннее сопротивление фазы А источника. Аналогично находят напряжения в двух других фазах:

На практике приемники подключают не к отдельному источнику, а к сети, питающейся от системы параллельно работающих генераторов. Поэтому обычно пренебрегают внутренними сопротивлениями фаз источников и считают фазные э. д. с. равными фазным напряжениям.

Чтобы найти связь между фазными и линейными напряжениями, при соединении источников э. д. с. звездой согласно с выбранными услов­ными положительными направлениями фазных и линейных напряжений по второму закону Кирхгофа можно записать следующие соотношения:

(4.5)

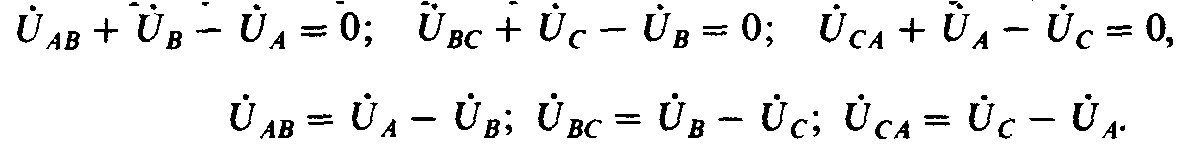
Для симметричных источников

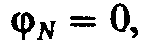
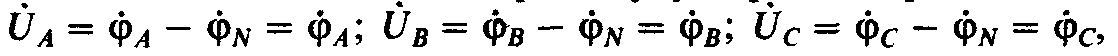
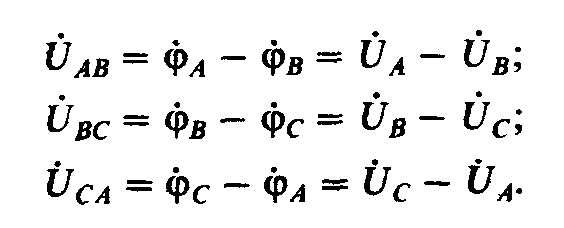
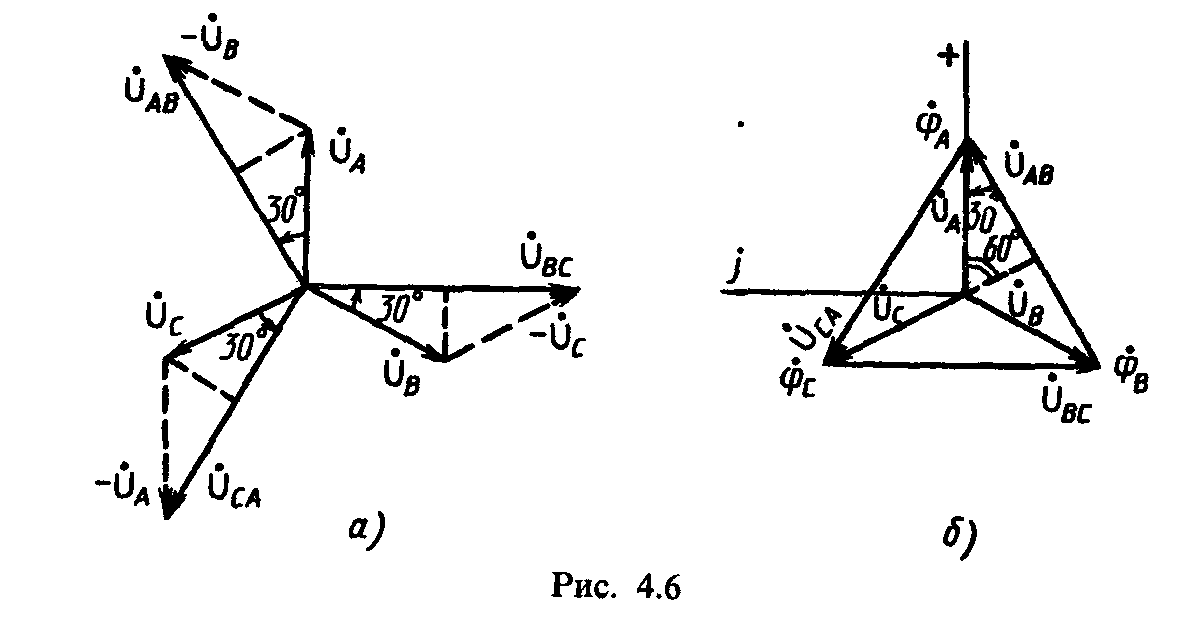
Если принять потенциал нейтральной точки источникато потенциалы начала его фаз будут равны фазным напряжениям:

а линейные напряжения равны:

(4.6)

По соотношениям (4.5), зная значения фазных напряжений, можно построить векторные диаграммы фазных и линейных напряжений источника при соединении его фаз звездой (рис. 4,6, а, б), которые будут представлять собой симметричную систему векторов, так как система фазных и линейных напряжений трехфазных генераторов, питающих электрическую сеть, вследствие их конструктивных особенностей сим­метрична.

Векторная диаграмма, представленная на рис. 4.6, а, соответствует симметричной системе фазных и линейных напряжений при соединении источников звездой. В этом случае на диаграмме как фазные, так и линей­ные напряжения соответственно равны и сдвинуты соответственно друг

относительно друга на угол 2л/3. Кроме того, из векторной диаграммы видно, что векторы линейных напряжений U_AB, U_BC, U_CA опережают по фазе соответственно векторы фазных напряжений U_A, U_B, Uc на угол 2π/6.

Векторную диаграмму фазных и линейных напряжений источника при соединении звездой можно представить и так, как показано на рис. 4.6, б, где линейные напряжения изображены векторами, соединяю­щими соответствующие векторы фазных напряжений.

Из векторных диаграмм рис. 4.6, а, б можно получить соотношение, связывающее между собой фазные и линейные напряжения симметрич­ного источника при соединении звездой. Так, для фазы A

В общем случае при соединении фаз симметричного источника звездой связь между линейными и фазными напряжениями описывается выражением

(4.7)

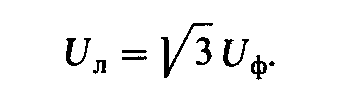
Таким образом, при соединении фаз симметричного источника звездой линейные напряжения в раз больше фазных напряжений. Для приемников низкого напряжения номинальными являются U_л = 380 B и U_ф = 220 B; U_л = 220 B и U_ф = 127 B.

Следует отметить, что в практике эксплуатации синхронных гене­раторов фазы их трехфазных обмоток соединяют только звездой, так как при отклонении э. д. с. источника от синусоидальной формы из-за наличия высших гармоник сумма мгновенных значений э. д. с. не будет равна нулю. При соединении фаз синхронного генератора треугольни­ком при холостом ходе в его обмотках будут возникать токи, которые будут вызывать их нагревание и снижение к. п. д. генератора.

Из рис. 4.5, б видно, что при соединении фаз источника треуголь­ником линейные напряжения равны фазным:

Итак, независимо от способа соединения фаз источника линейные напряжения между линейными проводами трехфазной цепи одинаковы и сдвинуты по фазе относительно друг друга на угол 2π/3, вследствие чего сумма их мгновен­ных значений или векторов всегда равна нулю. Однако значения линейных напряжений при соединении фаз источника треугольником будут в раз меньше, чем значения линейных напряжений при соединении фаз того же источника звездой.

Источник

№38 Способы соединения фаз трехфазных приемников.

Приемники трехфазного тока могут подключаться к генератору по двум схемам – звезды (y) и треугольника (Δ). Как известно, на выходе трехфазного генератора получаются два напряжение (линейное и фазное), отличающиеся в Uл/Uф = √3 раз. С другой стороны каждый приёмник энергии рассчитан на работу при определенном напряжении, которое называется номинальным. Схема соединения фаз приемника должна обеспечить подключение его фаз номинальное фазное напряжение. Таким образом, выбор схемы соединения фаз трехфазного приемника зависит от соотношения номинальных напряжений приемника и генератора (сети).

Схема звезды применяется в том случае, если номинальное напряжение приемника соответствует (равно) фазному напряжению генератора. При соединении в звезду концы фаз приемника объединяются в одну точку “n”, называемую нулевой или нейтральной, а начала фаз подключаются к линейным выводам трехфазного генератора А, В, С линейными проводами. Если нулевая точка приемника “n” соединена с нулевой точкой генератора “N” нулевым проводом, то схема получила название звезды с нулевым проводом (рис. 38.1а). При отсутствии нулевого провода схема носит название звезды без нулевого провода (рис. 38.1б).

Токи, протекающие в линейных проводах по направлению от генератора к приемнику, называются линейными.

Токи, протекающие в фазах приемника по направлению от начал к концам, называются фазными. В схеме звезды фазы приемника включены последовательно с линейными проводами и по ним протекают одни и те же токи (IA, IB, IC). Поэтому для схемы звезды понятия линейные и фазные токи тождественны: IЛ = IФ.

Ток, протекающий в нулевом проводе от приемника к генератору, называется нулевым или нейтральным (IN).

Напряжения между началами и концами фаз приемника называются фазными (UAn, UBn, UCn), а напряжения между началами фаз – линейными (UAB, UBC, UCA). Линейные напряжения приемника и генератора тождественно равны.

В схеме звезды с нулевым проводом (рис. 38.1а) к каждой фазе приемника подводится непосредственно фазное напряжение генератора (UAN = UAn = UA, UBN = UBn = UB, UCN = UCn = UC), каждая из фаз при этом работает независимо друг от друга, а линейные (фазные) токи определяются по закону Ома:

Ток в нулевом проводе в соответствии с первым законом Кирхгофа равен геометрической сумме линейных (фазных) токов:

При симметричной нагрузке ZA=ZB=ZC ток в нулевом проводе IN=0 и, следовательно, надобность в нeм отпадает. Симметричные трехфазные приемники (например, трехфазные электродвигатели) включаются по схеме звезды без нулевого провода.

При несимметричной нагрузке относительная величина тока в нулевом проводе зависит от характера и степени не симметрии фазных токов. Как правило, трехфазные приёмники стремятся спроектировать по возможности близкими к симметричным, поэтому ток в нулевом проводе в реальных условиях значительно меньше линейных (фазных) токов.

схеме звезды без нулевого провода (рис. 38.1б) при любой нагрузке фаз должно выполняться условие первого закона Кирхгофа:

Из уравнения следует вывод, что изменение одного из токов влечет изменение двух других токов, то есть отдельные фазы работают в зависимом друг от друга режиме. При несимметричной нагрузке потенциал нулевой точки приемника Un становится не равным нулю, он “смещается” на комплексной плоскости с нулевого положения, при этом фазные напряжения приемника (UAn, UBn, UCn) не равны соответствующим фазным напряжениям генератора (UA, UB, UC), происходит так называемый перекос фазных напряжений приемника (рис. 38.2).

Расчет токов и напряжений в схеме звезды без нулевого провода выполняется в следующей последовательности.

Определяется напряжение (потенциал) нейтральной точки приемника по методу двух узлов:

где ZN — комплексное сопротивление нулевого провода, при его отсутствии ZN=∞.

Фазные напряжения приемника определяются как разности потенциалов соответствующих точек:

UAn=UA-Un, UBn=UB-Un , UCn=UC-Un.

Фазные токи приемника определяются по закону Ома:

Комплексные мощности фаз приемника:

Режим работы приемника с перекосом фазных напряжений является ненормальным и может привести его к выходу из строя. По этой причине несимметричную трехфазную нагрузку запрещается включать по схеме звезды без нулевого провода (например, осветительную нагрузку).

Схема треугольника применяется в том случае, если номинальное фазное напряжение приемника соответствует (равно) линейному напряжению генератора. При соединении в треугольник конец каждой фазы соединяется с началом последующей, а точки соединения (вершины треугольника) подключаются к линейным выводам трехфазного генератора А, В, С линейными проводами (рис.38.3).

Токи, протекающие в фазах приемника по направлению от их начал к концам, называются фазными (IAB, IBC, ICA). Токи, протекающие в линейных проводах по направлению от генератора к приемнику, называются линейными (IA, IB, IC).

В схеме треугольника фазные и линейные напряжения приемника тождественно равны (UAB, UBC, UCA). В этой схеме к каждой фазе приемника подводится непосредственно линейное напряжение генератора, при этом отдельные фазы работают независимо друг от друга. Фазные токи определяются по закону Ома:

Линейные токи определяются из уравнений первого закона Кирхгофа для вершин треугольника, они равны геометрической разности фазных токов:

IA=IAB-ICA; IB=IBC-IAB; IC=ICA-IBC.

В симметричном режиме фазные и линейные токи симметричны, при этом отношение их модулей составляет IЛ/IФ = √3 .

При несимметричной нагрузке соотношение между линейными и фазными токами определяется уравнениями первого закона Кирхгофа. На рис. 38.4 показана векторная диаграмма токов и напряжений для произвольной трехфазной цепи при соединении фаз в треугольник.

Источник