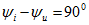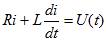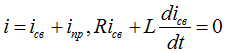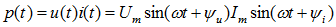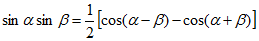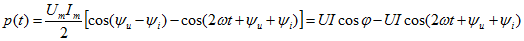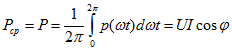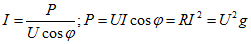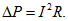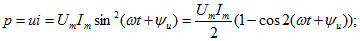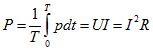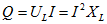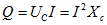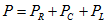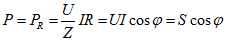- Способы соединения элементов электрических цепей
- Электрические цепи переменного тока
- Вектор напряжения на комплексной плоскости
- Кривые напряжения и тока в активном сопротивлении
- Кривые напряжения и тока в индуктивном сопротивлении
- Кривые напряжения и тока в емкостном сопротивлении
- Мощность цепи переменного тока
- Мощность цепи переменного тока
- Мощность в активном сопротивлении
Способы соединения элементов электрических цепей
Основные законы для цепей переменного тока
Закон Ома для участка цепи. Сила тока на данном участке цепи тем больше, чем больше сила тока на этом участке и чем меньше сопротивление участка.
Закон Ома для замкнутой цепи. Дело в том, что источник постоянного тока, будь то батарея или другой источник имеет свое сопротивление. Рассчитывая ток на этом участке необходимо учитывать и его. При этом зная ЭДС источника тока, получаем расчетную формулу для этого закона.
Первый закон Кирхгофа. Допустим, в один узел. Так вот, сумма всех токов, которые втекают в этот узел и вытекают из этого узла равна нулю. Или сумма токов, втекающих в узел равна сумме токов, вытекающих из этого узла.
Второй закон Кирхгофа
второй закон Кирхгофа — сумма падений напряжений на сопротивлениях потребителей в замкнутой цепи равна сумме ЭДС, выдаваемых источниками тока в этой цепи.
4. Закон Ома.
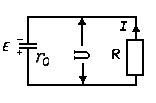
Закон Ома для участка цепи. Величина тока на участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению I=U/R , откуда U=IR ; R=U/I , где I –ток в цепи (А); U-напряжение на концах цепи (В); R-сопротивление участка цепи (Ом).
Закон Ома для всей цепи. Величина тока в неразветвленной цепи, содержащей один источник тока, прямо пропорциональна его ЭДС и обратно пропорциональна сопротивлению всей цепи: I=E/(R+r0), где E — ЭДС источника, r0 — внутреннее сопротивление источника.
Из этой формулы получается: IR=E — Ir0 , или U=E — Ir0
Напряжение на зажимах источника тока меньше его ЭДС на величину падения напряжения на внутреннем сопротивлении. При разомкнутой внешней цепи напряжение на зажимах источника тока равно его ЭДС.
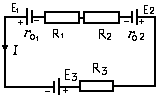
Ток в неразветвленной цепи, состоящей из нескольких последовательно соединенных источников тока и нескольких внешних сопротивлений, определяется по формуле: I= ΣE/(ΣR+Σr0) где ΣE=E1-E2+E3,
Где ΣR — сумма сопротивлений внешней цепи; Σr0 — сумма внутренних сопротивлений источников тока.
Закон Кирхгофа
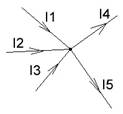
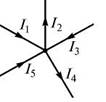
Первый закон Кирхгофа — алгебраическая сумма токов, сходящихся в любом узле, равна нулю.
Где i – число токов, сходящихся в данном узле. Например, для узла электрической цепи (рис. 1) уравнение по первому закону Кирхгофа можно записать в виде I1 — I2 + I3 — I4 + I5 = 0
Второй закон Кирхгофа:алгебраическая сумма падений напряжений на отдельных участках замкнутого контура, произвольно выделенного в сложной разветвленной цепи, равна алгебраической сумме ЭДС в этом контуре
где k – число источников ЭДС; m – число ветвей в замкнутом контуре; Ii, Ri – ток и сопротивление i-й ветви.
Способы соединения элементов электрических цепей
· Последовательное соединение — во всех его элементах протекает один и тот же ток, и во всем соединении нет ни одного промежуточного узла. Сопротивления при последовательном соединении складываются: 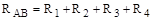
 |
· Параллельное соединение – это соединение, при котором напряжение на концах участка цепи одинаково. все элементы находятся под одним напряжением, сила тока распределена по-разному и при выходе одного из элементов все остальные продолжают свою работу.
При параллельном соединении эквивалентное сопротивление находится как:
В случае двух параллельно соединенных резисторов
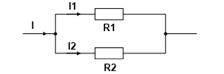
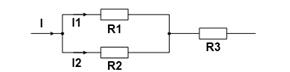
· Смешанное соединение –для нахождения эквивалентного сопротивления нужно, “свернуть” схему поочередным преобразованием параллельных и последовательных участков цепи.
Сначала найдем эквивалентное сопротивление для параллельного участка цепи, а затем прибавим к нему оставшееся сопротивление R3. Следует понимать, что после преобразования эквивалентное сопротивление R1R2 и резистор R3, соединены последовательно.
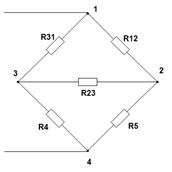
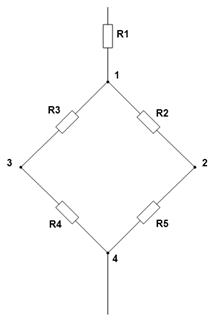
· Мостовая схема соединения представлена на рисунке ниже.
Для того чтобы свернуть мостовую схему, один из треугольников моста, заменяют эквивалентной звездой.
Затем находят общее эквивалентное сопротивление, учитывая, что резисторы R3,R4 и R5,R2 соединены между друг другом последовательно, а в парах параллельно.
Источник
Электрические цепи переменного тока
Переменный ток получил гораздо большее распространение в промышленности и в быту, чем постоянный, так как упрощается конструкция электродвигателей, а синхронные генераторы могут быть выполнены на значительно большие мощности и более высокие напряжения, чем генераторы постоянного тока. Переменный ток позволяет легко изменять величину напряжения с помощью трансформаторов, что необходимо при передаче электроэнергии на большие расстояния.
Электрический ток, возникающий под действием э. д. с, которая изменяется по синусоидальному закону, называют переменным. По существу, переменный ток — это вынужденные колебания тока в электрических цепях.
Амплитудой переменного тока называется наибольшее значение, положительное или отрицательное, принимаемое переменным током.
Периодом называется время, в течение которого происходит полное колебание тока в проводнике.
Частота — величина, обратная периоду.
Фазой называется угол 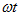
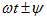
Периодический режим: 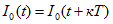
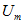
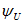
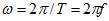
При f=50Гц T= 1/f=0,02 с, 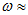
Расчет цепей переменного тока с использованием мгновенных значений тока, напряжения и ЭДС требует громоздкой вычислительной работы. Поэтому изменяющиеся непрерывно во времени токи, напряжения и ЭДС заменяют эквивалентными во времени величинами.
При расчете электрических цепей синусоидальную функцию выражают по формуле Эйлера через экспоненциальные функции:
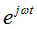
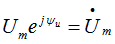
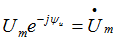
Таким образом, синусоидальное напряжение можно представить на комплексной плоскости вращающимся вектором. Тогда амплитудное значение напряжения 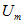
 Вектор напряжения на комплексной плоскости
Вектор напряжения на комплексной плоскости
Так как в цепи с синусоидальным напряжением ток тоже будет подчиняться этому закону, то аналогично можно записать
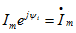
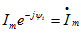
Разделив напряжение на ток, получим закон Ома в комплексном виде:
При 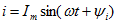
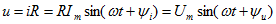
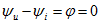
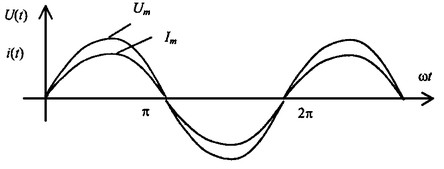
 Кривые напряжения и тока в активном сопротивлении
Кривые напряжения и тока в активном сопротивлении
Величину переменного напряжения или тока можно оценить значением амплитуды или средним значением за полупериод или действующим значением. При изменении напряжения или тока по закону синуса среднее значение напряжения определяется:
При большой частоте вращения ротора генератора, т. е. при большой частоте колебаний э. д. с. и силы тока, измерять их амплитуды на практике крайне неудобно. По этой причине ввели величины, названные действующими значениями э. д. с, силы тока и напряжения.
Действующим значением силы переменного тока называют силу такого постоянного тока, при прохождении которого по той же цепи и за то же время выделяется такое же количество теплоты, как и при прохождении переменного тока.
При синусоидальном законе действующие значения тока и напряжения:
Приборы электромагнитной системы, применяемые для измерений напряжений и токов на переменном токе, регистрируют действующие значения. Соответственно градуируются и шкалы этих приборов.
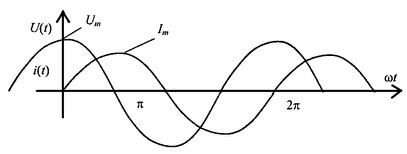
Ток, протекающий через индуктивность L (рис. 7), меняется по закону синуса /’ = Im sin(co/ + у;).
Кривые напряжения и тока в индуктивном сопротивлении
Напряжение на индуктивности определяется выражением
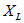
Индуктивное сопротивление выражают в омах, оно играет роль сопротивления в цепи переменного тока с катушкой индуктивности.
В идеальной индуктивности ток отстает от напряжения на 90°.
Если напряжение на емкости меняется по закону синуса 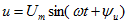
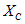
Емкостное сопротивление выражается в омах, оно играет роль сопротивления в цепи переменного тока с конденсатором.
 Кривые напряжения и тока в емкостном сопротивлении
Кривые напряжения и тока в емкостном сопротивлении
В идеальной емкости ток опережает напряжение на 90°
Режим — состояние электрической цепи переменного тока описывается дифференциальными уравнениями, представляющими собой уравнения с постоянными коэффициентами и правой частью, например:
Из курса высшей математики известно, что общее решение такого уравнения может быть найдено методом наложения принужденного и свободного режимов:
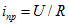
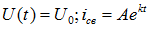
Свободные процессы исследуются с целью определения устойчивости системы. В устойчивой системе процессы должны затухать. Принужденный и свободный режимы в сумме определяют процессы, которые называются переходными, т.е. осуществляется переход от одного установившегося режима к другому.
При установившемся режиме ток и напряжение сохраняют в течение длительного времени амплитудные значения.
В цепях постоянного тока токи и напряжения остаются неизменными, а в цепях переменного тока остаются неизменными кривые изменения токов и напряжений.
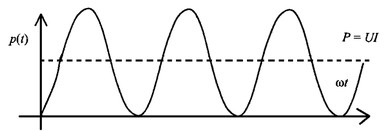
Мощность цепи переменного тока
В периодическом синусоидальном режиме
Используя известное тригонометрическое преобразование
и обозначив 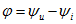
Среднее за период значение гармонической функции удвоенной частоты равно нулю.
Измерение мгновенного значения мощности переменного тока затруднено из-за сравнительно большой частоты колебаний (v = 50 Гц). Поэтому на практике принято пользоваться средней мощностью тока. Средняя мощность — это отношение энергии, потребляемой за один период, к периоду:
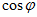
Потребляемая на участке цепи с резистором средняя мощность получила название активной мощности. Она необратимо преобразуется в джоулеву теплоту и другие виды энергии. Мощность, потребляемую на участках цепи с емкостным и индуктивным сопротивлениями, называют реактивной мощностью.
При передаче электрической энергии по цепи переменного тока ее необратимые преобразования происходят только на тех участках цепи, которые содержат резисторы. Такие участки цепи называют активной нагрузкой. На активной нагрузке электроэнергия превращается в теплоту или механическую работу.
Участок цепи с индуктивностью или емкостью называют реактивной нагрузкой. На участках цепи, которые состоят из чистых емкостных или индуктивных сопротивлений, электроэнергия не потребляется. В цепи с реактивными нагрузками происходит только перекачка энергии от генератора к нагрузке и обратно с неизбежными потерями в подводящих проводах.
При заданных Р и U ток является функцией cosj. Потери мощности на сопротивлении
В цепи с резистором j=0.
Коэффициент мощности cosj показывает, какая часть полной мощности, вырабатываемой генератором и передаваемой нагрузке, необратимо используется нагрузкой. Он играет важную роль в электротехнике. В самом деле, если в цепи имеется значительный сдвиг по фазе между колебаниями тока и э. д. с, то коэффициент мощности мал и нагрузка потребляет от генератора малую активную мощность. Вместе с тем генератор должен вырабатывать полную мощность S. Эту же мощность должен отдавать генератору первичный двигатель. Таким образом, при низком коэффициенте мощности нагрузка потребляет лишь часть энергии, которую вырабатывает генератор. Оставшаяся часть энергии перекачивается периодически от генератора к потребителю и обратно и рассеивается в линиях электропередачи.
Максимально благоприятные условия передачи электроэнергии создаются в цепи, работающей в режиме резонанса. В самом деле, при приближении к резонансу амплитуда силы тока оказывается максимальной и коэффициент мощности стремится к единице. В этом случае активная мощность приближается к полной мощности, т. е. достигает максимума.
Повышение к. м. является важной народнохозяйственной задачей, от решения которой зависит эффективность использования вырабатываемой электроэнергии.
Уменьшение к. м. в промышленных цепях происходит в основном за счет содержащихся в них трансформаторов и асинхронных электродвигателей, имеющих значительные индуктивные сопротивления. Поэтому повысить к. м. при таких нагрузках можно путем подключения параллельно основной цепи компенсирующих конденсаторов, позволяющих приблизиться к режиму резонанса токов.
С целью повышения к. м. и экономии электроэнергии не следует допускать холостого хода (т. е. работы без нагрузки) трансформаторов и асинхронных электродвигателей, ибо в этом случае они представляют собой чисто индуктивные сопротивления и вызывают дополнительные потери мощности.
Коэффициент мощности (к. м.) ни в коем случае нельзя путать с коэффициентом полезного действия (к. п. д.). Так, например, при определенном соотношении емкости и индуктивности коэффициент мощности в данной цепи может оказаться равным единице. Коэффициент же полезного действия цепи всегда меньше единицы.
Мощность цепи переменного тока
Мощность в активном сопротивлении
Мгновенное значение мощности для цепи с резистором:
Из рисунка видно, что потребляемая резистором мгновенная мощность остается все время положительной, но пульсирует с удвоенной по отношению к силе тока и э. д. с. частотой.
Действующее значение мощности:
Активная мощность в цепи с идеальной катушкой индуктивности и конденсатором равна 0. Реактивная мощность определяется выражением:
Аналогично можно проделать для цепи с идеальным конденсатором:
В произвольной цепи переменного тока потребляемая одновременно активной и реактивной нагрузками суммарная мощность
Но так как 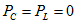
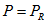
где S — полная мощность, вырабатываемая генератором переменного тока, ВА;
a — сдвиг по фазе между колебаниями э. д. с. и силы тока.
Источник

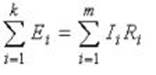
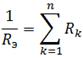
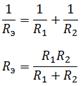
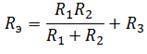
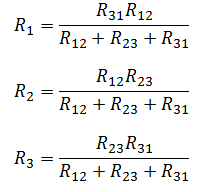
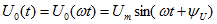
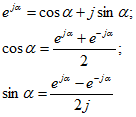
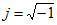
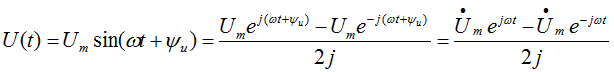
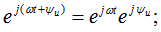
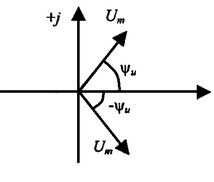 Вектор напряжения на комплексной плоскости
Вектор напряжения на комплексной плоскости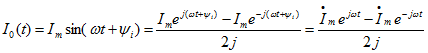
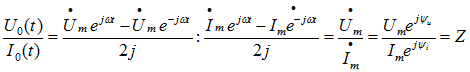
 Кривые напряжения и тока в активном сопротивлении
Кривые напряжения и тока в активном сопротивлении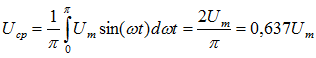
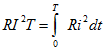
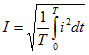
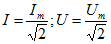
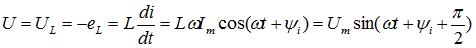
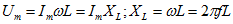
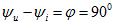
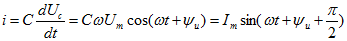
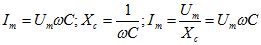
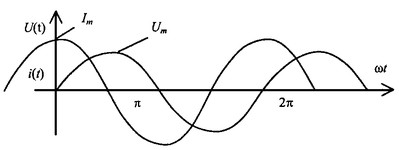 Кривые напряжения и тока в емкостном сопротивлении
Кривые напряжения и тока в емкостном сопротивлении