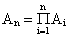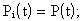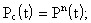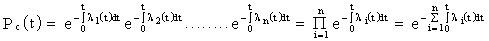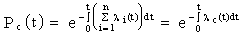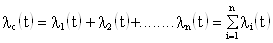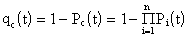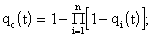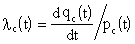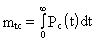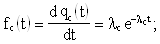Топология систем управления. Способы соединения элементов
Символическое изображение всех функциональных элементов и связей между ними, отражающее последовательность взаимодействия процессов в системе управления, называется функциональной или структурной схемой.
Если известна структурная схема и параметры системы, то можно, пользуясь аппаратом структурных преобразований, найти передаточную функцию любой системы.
При исследовании линейных систем важно уметь приводить структурные схемы к форме наиболее удобной для расчетов. Для этого необходимо научиться заменять одни структурные схемы на равноценые, но более удобные для проводимых расчетов или проводимого моделирования, что позволяет значительно упростить определение характеристик систем и сократить объем необходимых для этого вычислений. Всякая структурная схема представляет собой совокупность более простых структур, точек разветвления, сумматоров, соединенных между собой различными способами. Любое преобразование структурной схемы сводится к эквивалентной перестановке различных ее соседних элементов. Точки разветвления линейных систем называются узлами. Основной принцип перестановки элементов структурной схемы состоит в том, что все входные и все выходные переменные преобразуемого участка должны остаться неизменными. Одномерной системой управления называется система, имеющая один контур управления, то есть система с одной управляемой координатой и одним задающим воздействием. Многомерной САУ называется такая система управления, у которой несколько управляемых параметров. Рассмотрим способы соединения элементов в схеме и формулы передаточных функций типовых соединений.
Последовательное соединение
Рис. 1.11. Схема последовательного соединения звеньев
Передаточная функция последовательного соединения равна произведению передаточных функций входящих в соединение звеньев.
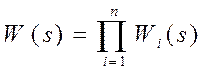 | (1.9) |
Параллельное соединение
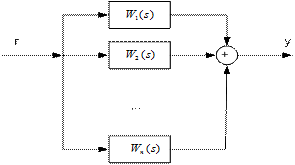
Рис. 1.12. Схема параллельного соединения звеньев
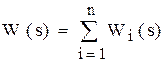 | (1.10) |
Передаточная функция параллельного соединения равна сумме передаточных функций входящих в соединение звеньев.
Соединение с обратной связью
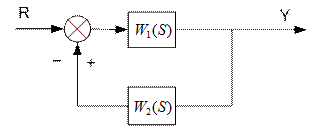
Рис. 1.13. Схема соединения звеньев с обратной связью
Передаточная функция обратного соединения равняется отношению передаточной функции звена в прямой цепи к произведению передаточных функций звеньев, стоящих в прямой и обратной цепи со знаком + для отрицательной обратной связи и со знаком — для положительной обратной связи, увеличенному на единицу:
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Способы соединения элементов САР
При решении задач анализа САР ее удобно представлять в виде структурной схемы (структурной динамической схемы), которая является графическим отображением математической модели системы. Имея такую модель и зная динамические характеристики отдельных звеньев, составляющих структурную схему, можно определить динамические характеристики САР.
Отдельные звенья на такой схеме условно обозначают в виде прямоугольников, внутри которых записывают выражения передаточной функции. Входные и выходные сигналы для каждого звена выражают в определенной форме, т.е. в виде изображений X(P) и Y(P). Устройство сравнения изображают в виде круга, разделенного на четыре сектора. Сектор, куда подается вычитаемая величина, обозначают знаком «-» или затушевывают.
Основными видами соединений звеньев являются: последовательное, параллельное и соединение с обратной связью (встречно-параллельное).
При последовательном соединении выход первого звена подсоединяется к входу последующего и т. д. (см. рис. 13.13). При таком соединении передаточные функции отдельных звеньев перемножаются. Произведение будет являться передаточной функцией всего соединения.
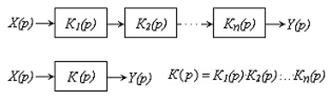 |
| Рис. 13.13 – Последовательное соединение динамических звеньев |
При параллельном соединении входы всех звеньев подсоединяются к источнику входного воздействия и образуют общий вход, а выходы соединяются вместе и являются общим выходом данного соединения (Рис. 13.14). Передаточной функцией всей цепи является алгебраическая сумма передаточных функций звеньев.
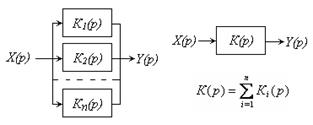 |
| Рис. 13.14 – Параллельное соединение динамических звеньев |
При соединении с обратной связью (ОС) выход одного звена через другое звено (звено обратной связи) связывается с его входом (рис. 13.15). При этом, если сигнал обратной связи вычитается из входного воздействия, обратная связь будет отрицательной (ООС), если складывается — положительной (ПОС).
Вид связи очень сильно влияет на вид характеристик и динамические свойства систем. Так при ООС повышается быстродействие системы и она становится более устойчивой к внешним воздействиям. Введение ПОС ухудшаются динамические свойства и устойчивость системы снижается.
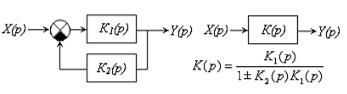 |
| Рис. 13.15 – Соединение с обратной связью |
В выражении для передаточной функции всего соединения (13.1) знак «+» ставится при ООС, а знак «-» соответствует ПОС, то есть
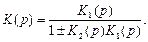
Произведение К2(р)·К1(р), входящее в формулу (13.1), называется передаточной функцией разомкнутой системы и обозначается как КР(р), то есть
Входящая в выражения (13.1) и (13.2) функция К1(р) называется передаточной функцией прямой цепи.
Если К2(р) = 1, т.е. выход звена К1(р) cвязан непос-редственно с его входом, то передаточная функция системы упрощается. Тогда можно записать, что
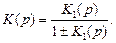
Рассмотренные преобразования различных видов соеди-нений звеньев позволяют упростить структурную динами-ческую схему САР. Основное условие преобразования — неизменность динамических характеристик системы.
Устойчивость САР
Под устойчивостью системы понимают ее способность восстанавливать состояние равновесия после прекращения внешнего воздействия.
Для линейной системы связь между входным воздействием х(t) и выходной величиной y(t) описывается линейным дифференциальным уравнением (ЛДУ) n-го порядка:
где a0…an — коэффициенты, характеризующие параметры системы; b0…bm – коэффициенты, определяющие параметры входного воздействия, причем m ≤ n.
Решение ЛДУ представляется в виде двух составляющих – свободной yсв (t) и принужденной yпр (t):
Свободная составляющая характеризует свободное состо-яние системы, не зависящее от внешнего воздействия и опреде-ляемое только свойствами системы.
Устойчивость системы определяется ее поведением после прекращения входного воздействия, т.е. когда x(t)=0. В этом случае ЛДУ системы будет иметь вид:
Решение этого уравнения – свободная составляющая, характеризующая переходный процесс. Она будет иметь вид:
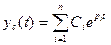
где Сi – постоянные интегрирования, определяемые пара-метрами системы; рi — корни характеристического уравнения
в котором оператор р заменяет операцию дифференцирования.
Из выражения (13.7) видно, что характер поведения системы, т.е. yс(t) зависит от корней рi уравнения (13.8).
В общем случае корни этого уравнения являются комплексно сопряженными, тоесть
где αi — действительная часть; βi – мнимая часть.
Если корни рi действительные (βi = 0), тогда
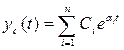
При этом, если для всех корней αi 0, то с течением времени (t → ∞) процесс yс(t) будет нарастать, что свидетельствует о неустойчивости системы. Если хотя бы один корень рi = 0, то система будет находиться на границе устойчивости. В случае, когда имеются комплексные корни, тогда в решении yс(t) появятся соответствующие им слагаемые вида:
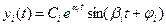
где 
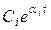
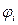
Характер этого колебания будет зависеть от 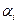
— при 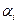
— если
Дата добавления: 2016-01-18 ; просмотров: 1689 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник
Виды соединения элементов в систему
1.17 Виды соединения элементов в систему
1) Последовательное соединение.
2) Паралельное соединение.
1.17.1 Последовательное соединение элементов в систему
Соединение элементов называется последовательным, если отказ, хотя бы одного элемента приводит к отказу всей системы. Система последовательно соединённых элементов работоспособна тогда, когда работоспособны все её элементы.
Рассчитаем надёжность системы при последовательном соединении элементов в систему. Рассчитать надёжность системы — это значит по заданным количественным характеристикам надёжности элементов определить количественные характеристики надёжности системы.
Рассмотрим события 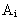
Событие 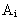
Считаем, что события 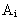
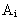
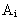
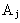
В этом случае элементы системы называются независимыми в смысле надёжности.
Рассмотрим событие А.
Событие А означает безотказную работу системы из n последовательно соединённых элементов за время t.
Событие А имеет место, если одновременно выполняются события 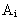
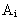
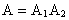
Из теории вероятностей известно, что в этом случае
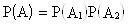
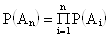
Обозначим 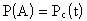
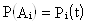
Откуда 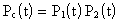
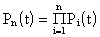
Т.о., вероятность безотказной работы системы за время t равна произведению вероятностей безотказной работы за время t элементов системы.
В частном случае, когда все элементы системы одинаковы, имеем
Выразим вероятность безотказной работы элементов 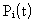
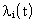
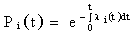
Запишем формулы для определения вероятности безотказной работы системы 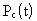
или
где
Здесь 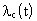
Т.о., при последовательном соединении элементов их интенсивность отказов складывается, и интенсивность отказов системы есть сумма интенсивностей отказов элементов системы.
Вероятность отказа системы на интервале времени (0, t) равна
или
Интенсивность отказов 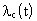
Среднее время безотказной работы системы
В случае экспоненциального закона надёжности всех элементов имеем:
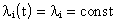
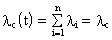
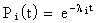
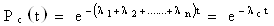
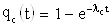
Т.о. закон распределения времени безотказной работы системы является экспоненциальным.
Определим среднее время безотказной работы системы. Имеем
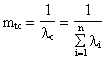
Источник