Структурные схемы. Способы соединения звеньев
Систему автоматического управления можно рассматривать как комбинацию типовых динамических звеньев. Изображение системы управления в виде совокупности типовых и нетиповых динамических звеньев с указанием связей между ними носит название структурной схемы системы. Звено в этом случае выступает как элементарная структурная единица, преобразователь информации.
Структурные схемы состоят из отдельных структурных элементов. Основными элементами структурных схем являются следующие.
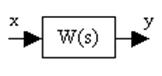
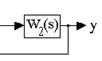
1. Звено с одним входом и одним выходом: Y(s)=W(s)X(s).
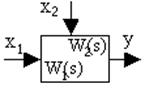
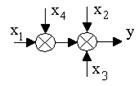
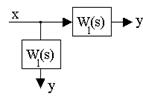
2. Звено с двумя входами и одним выходом (около каждого входа записывается своя передаточная функция):Y(s)=W1(s)X1(s)+W2(s)X2(s)
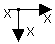
3. Линия связи и узел (разветвление), стрелка показывает направление передачи информации.
и 
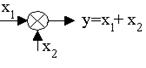
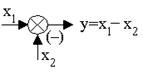
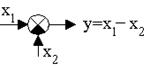
5. Элемент сравнения.
или 
В системах управления встречаются три вида соединений звеньев: последовательное, параллельное и соединение по схеме с обратной связью.
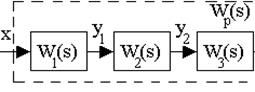
Последовательное соединение звеньев изображено на рис.3.10, такое соединение характеризуется тем, что выход предыдущего звена подается на вход последующего.
Рис. 3.10. Последовательное соединение звеньев
Выходная величина последовательно соединенных звеньев определяется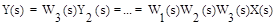 
.
Откуда результирующая передаточная функция 
равняется
.
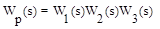
Следовательно, в общем случае можно записать
, (3.51)
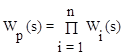
где n — число включенных последовательно звеньев.
Таким образом, результирующая передаточная функция последовательно соединенных звеньев равна произведению передаточных функций составляющих звеньев.
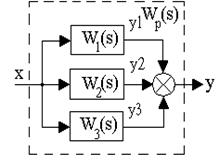
Параллельное соединение звеньев изображено на рис.3.11, такое соединение характеризуется тем, что на входы всех звеньев подается одно и то же входное воздействие, а выходная величина определяется суммой выходных величин отдельных звеньев.
Рис. 3.11. Параллельное соединение звеньев
Выходная величина параллельно соединенных звеньев определяется y=y1+y2+y3, т.е.
.
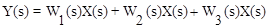
Тогда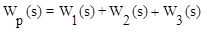 
.
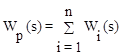
, (3.52)
где n — число включенных параллельно звеньев.
Таким образом, результирующая передаточная функция параллельно соединенных звеньев равна сумме передаточных функций составляющих звеньев.
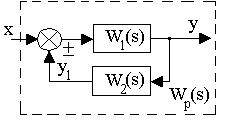
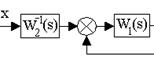
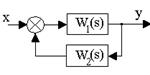
Обратная связь. Такое соединение звеньев изображено на рис.3.12, оно характеризуется тем, что выходной сигнал звена подается на его вход.
Рис. 3.12. Соединение звеньев по схеме с обратной связью
Обратная связь может быть положительной (ПОС), если сигнал y1, снимаемый с выхода второго звена, суммируется с сигналом x на входе, и отрицательной (ООС), если y1 вычитается. Кроме того, обратные связи могут быть жесткими и гибкими. Связь называется гибкой, если передаточная функция W2(s) в установившемся режиме равна нулю.
Для определения результирующей передаточной функции такой комбинации звеньев запишем очевидные соотношения:
,
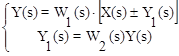
где знак “+” относится к положительной, а знак “-” — к отрицательной обратной связи.
Откуда результирующая передаточная функция обратной связи имеет вид
, (3.53)
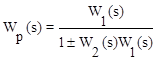
где знак “+” соответствует ООС, знак “-” — ПОС.
В общем случае, сложная цепь динамических звеньев, образующих систему управления, включает в себя комбинации всех трех рассмотренных случаев, т.е. представляет собой смешанное соединение звеньев. Пользуясь выражениями (3.51), (3.52) и (3.53), можно найти общую результирующую передаточную функцию смешанного соединения звеньев.
В тех случаях, когда структурная схема системы оказывается сложной и содержит перекрестные связи, ее упрощают и сводят к простейшему эквивалентному виду, пользуясь правилами преобразования структурных схем [1,2,7].
Основные правила эквивалентного преобразования структурных схем.
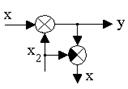
1. Перенос сумматора:
Þ 
Þ 
Þ 
Þ 
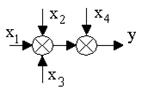
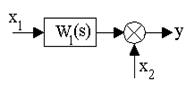
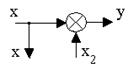
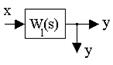
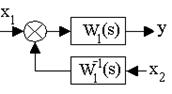
3. Преобразование к единичной обратной связи.
Þ 
Источник
3.2. Способы соединения элементарных динамических звеньев
Последовательное соединение звеньев.Покажем, что произведение двух передаточных функций
и
равно передаточной функции объекта
, образованного путем последовательного соединения двух объектов (рис. 3.9.), один из которых имеет передаточную функцию
а другой –
.
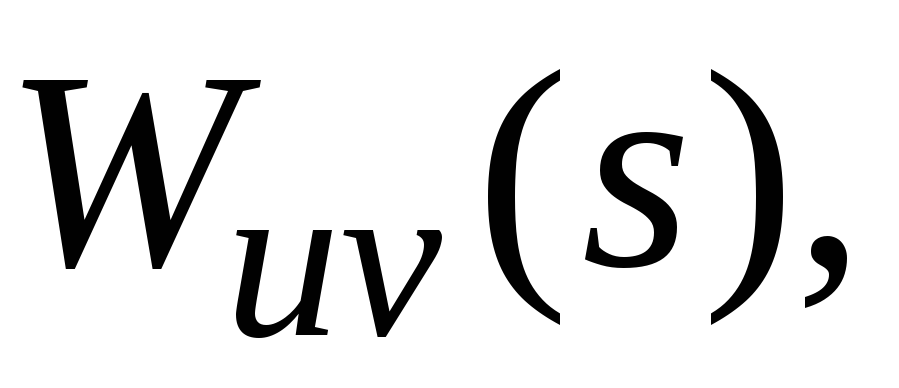
Рис. 3.9. Структурная схема последовательного соединения объектов.
Действительно, передаточная функция составного объекта 
, представленного на рис. 3.9, определяется выражением
. (3.21)
;
,
то с учетом выражения (3.21) получим равенство
.
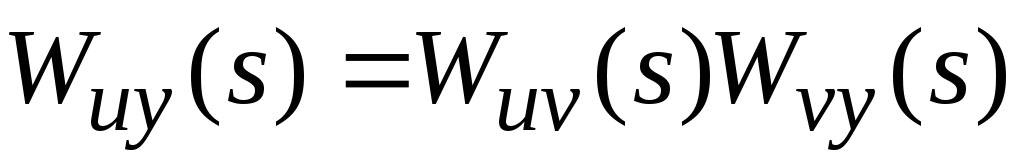
Рассуждая аналогичным образом можно показать, что если имеется 
последовательно соединенных объектов с передаточными функциями
,
, то передаточная функция составного объекта
задается равенством
. (3.22)
Параллельное соединение звеньев. Этот способ соединения звеньев представлен на рис. 3.10.
Рис. 3.10. Структурная схема параллельного соединения объектов.
В данном случае передаточная функция составного объекта 
определяется выражением
. (3.23)
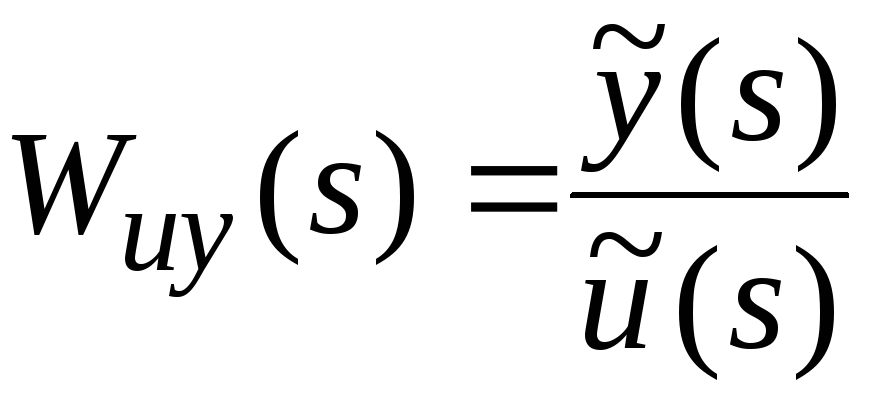
Кроме того, передаточные функции параллельно соединенных объектов задаются следующими выражениями:
;
. (3.24)
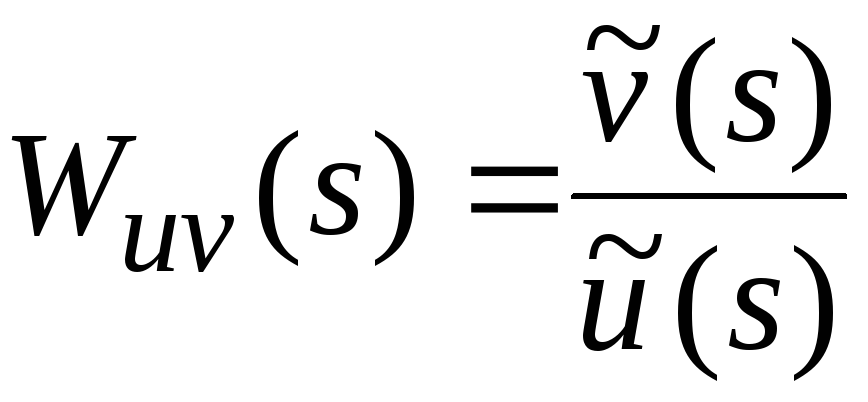
Согласно рис. 3.3. должно выполняться равенство
. (3.25)
С учетом выражений (3.24) равенство (3.25) принимает вид
. (3.26)
Принимая во внимание выражение (3.23) из равенства (3.26) получим
. (3.27)
Таким образом, согласно выражению (3.27) передаточная функция объекта, состоящего из двух параллельно соединенных объектов (звеньев) равна сумме их передаточных функций.
Путем аналогичных рассуждений можно показать, что если имеется 
последовательно соединенных объектов с передаточными функциями
,
, то передаточная функция составного объекта
задается равенством
. (3.28)
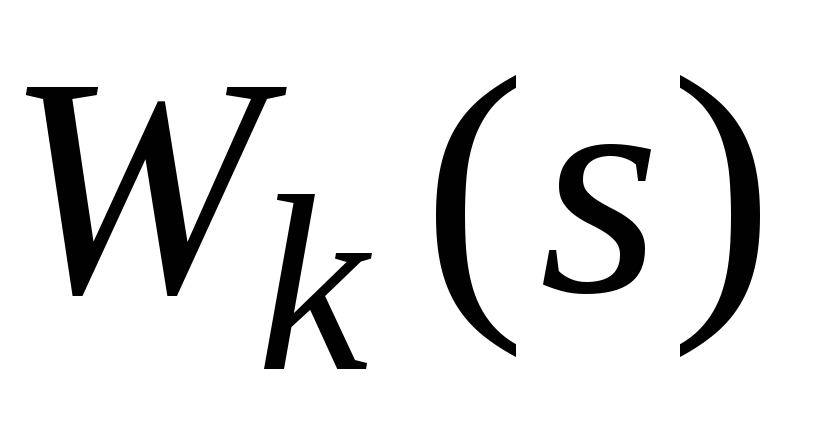
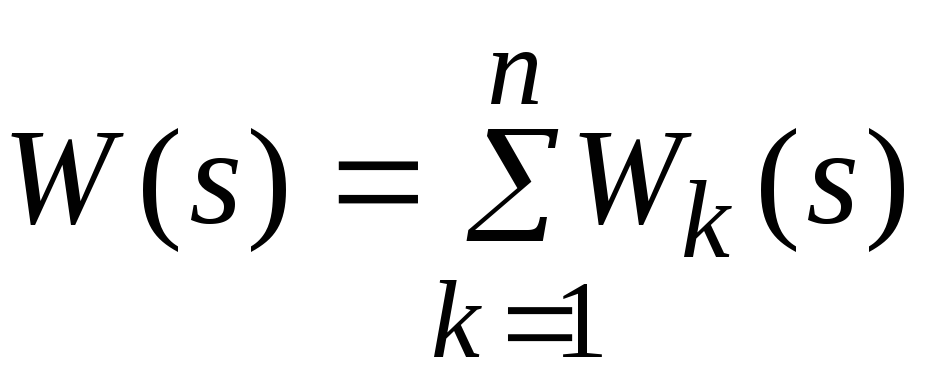
Обратно, если представить передаточную функцию объекта 
как сумму передаточных функций
,
, то тем самым исходный объект разбивается на
параллельно соединенных звеньев.
Таким образом, располагая структурной схемой объекта, на которой показан способ соединения составляющих его звеньев, можно определить передаточную функцию объекта, если известны передаточные функции звеньев. Кроме того, при конструировании объектов с желаемыми динамическими свойствами удобно бывает представить его в виде комбинации различных звеньев с известными динамическими характеристиками.
Соединение звеньев по способу обратной связи.При таком соединении одно из звеньев (звено обратной связи) передает сигнал с выхода другого звена на его вход, где они суммируются с входным воздействием соединения (рис. 3.11). Пусть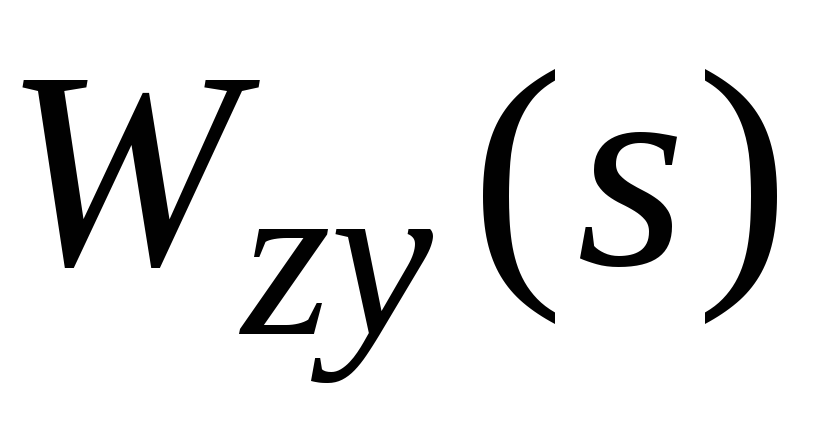
– передаточная функция звена, а
– передаточная функция звена обратной связи, тогда для изображений
и
входного
и выходного
сигналов выполняется равенство
. (3.29)
Рис. 3.11. Соединение звеньев по способу обратной связи.
Согласно равенству (3.29) имеем
. (3.30)
На основании равенства (3.30) можно сделать вывод, что передаточная функция рассматриваемого соединения звеньев 
определяется выражением
. (3.31)
Отметим, что обратная связь называется отрицательной, если выполняется равенство
,
обратную связь принято называть положительной.
При наличии отрицательной обратной связи в знаменателе выражения (3.31) ставится знак «плюс», а если обратная связь положительная, то знак «минус».
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
Источник
