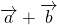Сложение векторов
Часть математических и физических задач содержит необходимость математических действий с векторами (сложение и вычитание).
Проиллюстрируем сложение. Пусть даны вектора и , попытаемся найти вектор .
Способ 1. Метод сложения треугольником
Возьмём необходимые вектора и параллельным переносом совместим конец первого вектора ( ) и начало второго ( ) (рис. 1)
Рис. 1. Сложение векторов (правило треугольника)
Тогда вектор, соединяющий начальную точку первого вектора ( ) и конец второго ( ), является вектором ( ).
Способ 2. Метод сложения параллелограммом
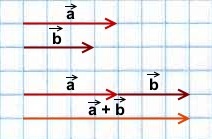
Возьмём необходимые вектора и параллельным переносом совместим начало первого вектора ( ) и начало второго ( ) (рис. 2). Параллельным переносом совместим конец каждого вектора с началом другого.
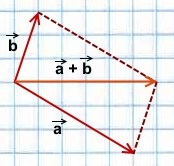
Рис. 2. Сложение векторов (правило параллелограмма)
Тогда вектор, соединяющий общую начальную точку первого ( ) и второго ( ) векторов и общий конец данных векторов, является вектором суммы ( ).
Вывод: в ряде задач, где присутствуют несколько однородных векторных физических величин, часто необходимо найти общий вектор (общую скорость, равнодействующую силу, полный вектор магнитной индукции или электрической напряжённости поля). Тогда необходимо сначала сложить вектора, а потом найти модуль получившегося вектора.Чаще всего первый метод используется в кинематике (сложение скоростей). Второй метод часто используют в динамике.
Источник
Сложение и вычитание векторов
Теорема 1 От любой точки \( K \) можно отложить вектор единственный \( \overrightarrow \) .
Существование: Имеем два следующих случая:
Здесь получаем, что искомый нами вектор совпадает с вектором \( \overrightarrow
Из данного выше построения сразу же будет следовать единственность данного вектора.
Сумма векторов. Сложение векторов. Правило треугольника
Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма.
Суммой нескольких векторов \( \vec
Такая операция выполняется по правилу многоугольника.
Сумма векторов в координатах
При сложении двух векторов соответствующие координаты складываются.
\( \vec + \vec = \left( <
Отметим несколько свойств сложения двух векторов:
Для произвольного вектора \( \overrightarrow \) выполняется равенство
Для произвольных точек \( A,\ B\ и\ C \) справедливо следующее равенство
Замечание Таким способом также можно строить сумму любого числа векторов. Тогда оно будет носить название правила многоугольника.
Разность векторов. Вычитание векторов
Разность двух одинаковых векторов равна нулевому вектору :
\( \vec — \vec = \vec <0>\)
Длина нулевого вектора равна нулю:
\( \left| \vec <0>\right| = 0 \)
Разность векторов в координатах
При вычитании двух векторов соответствующие координаты также вычитаются.
\( \vec — \vec = \left( <
Умножение вектора на число
Пусть нам дан вектор \( \overrightarrow
Определение Произведением вектора \( \overrightarrow
Длина вектора \( \overrightarrow
Векторы \( \overrightarrow
Обозначение: \( \ \overrightarrow
Источник
Сумма и разность векторов
В данной публикации мы рассмотрим, как найти сумму и разность векторов, приведем геометрическую интерпретацию, а также формулы, свойства и примеры этих действий.
Сумма векторов
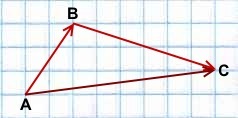
Сложение векторов выполняется по правилу треугольника.
Геометрическая интерпретация:
Суммой a и b является вектор c , начало которого совпадает с началом a , а конец – с концом b . При этом конец вектора a должен совпадать с началом вектора b .
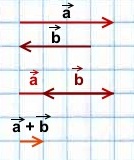
Для сложения векторов также используется правило параллелограмма.
Два неколлинеарных вектора a и b можно привести к общему началу, и в этом случае их суммой является вектор c , совпадающий с диагональю параллелограмма и берущий начало в той же точке, что и исходные векторы.
Формула сложения векторов
Элементы вектора c равняются попарной сумме соответствующих элементов a и b .
| Для плоских задач | Для трехмерных задач | Для n-мерных векторов |  Если из вектора a вычесть b , то получится c , причем должно соблюдаться условие: Формула вычитания векторовЭлементы вектора c равны попарной разности соответствующих элементов a и b .
|













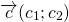
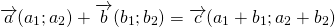
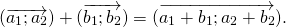
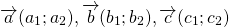
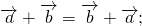
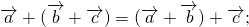
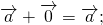
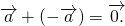
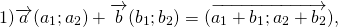
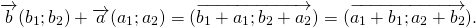
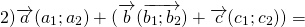
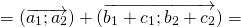
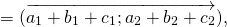
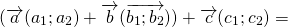
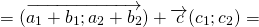
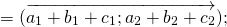
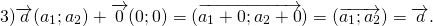
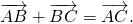

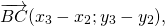
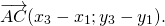
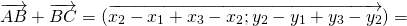
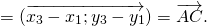
 Например,
Например,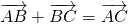
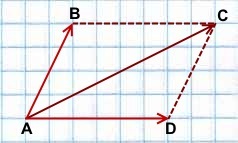 Например,
Например,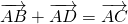
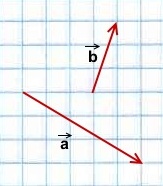 Построить сумму векторов
Построить сумму векторов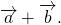
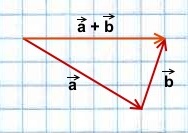
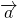
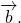
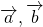
 Сумма
Сумма