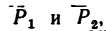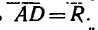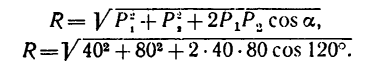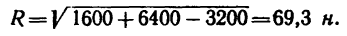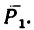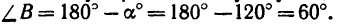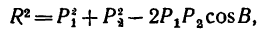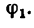Способы сложения сил техническая механика

Сложение сил

Способы сложения сил:

Если две или более сил направлены в одну сторону, их просто складывают. Вы толкаете автомобиль и его толкают еще несколько человек в ту же сторону, силы складываются, автомобиль катится.

Или если все вместе поднимают тяжелый шкаф или телевизор. В одну сторону действует подъемная сила, а в противоположную сторону сила тяжести. Тогда происходит вычитание силы тяжести из ваших сил. И только когда ваша совокупная сила подъема станет больше силы тяжести, телевизор будет поднят.

Если силы будут одинаковыми, но разнонаправленными, то тело будет оставаться в покое: кто-то толкает тело с одной стороны, кто-то с другой, если сила равна, тело останется на месте.

Редактировать этот урок и/или добавить задание Добавить свой урок и/или задание

Добавить интересную новость

Добавить анкету репетитора и получать бесплатно заявки на обучение от учеников

user->isGuest) < echo (Html::a('Войдите', ['/user/security/login'], ['class' =>»]) . ‘ или ‘ . Html::a(‘зарегистрируйтесь’, [‘/user/registration/register’], [‘class’ => »]) . ‘ , чтобы получать деньги $$$ за каждый набранный балл!’); > else < if(!empty(\Yii::$app->user->identity->profile->first_name) || !empty(\Yii::$app->user->identity->profile->surname))< $name = \Yii::$app->user->identity->profile->first_name . ‘ ‘ . \Yii::$app->user->identity->profile->surname; > else < $name = ''; >echo ‘Получайте деньги за каждый набранный балл!’; > ?>—>

Добавление комментариев доступно только зарегистрированным пользователям

Lorem iorLorem ipsum dolor sit amet, sed do eiusmod tempbore et dolore maLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborgna aliquoLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempbore et dLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborlore m mollit anim id est laborum.

28.01.17 / 22:14, Иван Иванович Ответить +5

Lorem ipsum dolor sit amet, consectetu sed do eiusmod qui officia deserunt mollit anim id est laborum.

28.01.17 / 22:14, Иван ИвановичОтветить -2

Lorem ipsum dolor sit amet, consectetur adipisicing sed do eiusmod tempboLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod temLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborpborrum.

28.01.17 / 22:14, Иван Иванович Ответить +5

Источник

Способы сложения сил техническая механика

Сложение сил производят, используя правило сложения векторов. Или так называемое правило параллелограмма. Так как сила изображается в виде вектора, то есть это отрезок, длинна которого показывает числовое значение силы, а направление указывает направление действия силы. То складывают силы, то есть вектора, с помощью геометрического суммирования векторов. С другой стороны сложение сил это нахождение равнодействующей нескольких сил. То есть когда на тело действует несколько разных сил. Разных как по величине, так и по направлению.

Момент силы относительно оси или просто момент силы называется проекция силы на прямую, которая перпендикулярна радиусу и проведена в точке приложения силы умноженная на расстояние от этой точки до оси. Либо произведение силы на плечо ее приложения. Плечо в данном случае это расстояние от оси до точки приложения силы. Момент силы характеризует вращательное действие силы на тело. Ось в данном случае это место крепления тела, относительно которого оно может совершать вращение. Если тело не закреплено, то осью вращения можно считать центр масс.

Импульс тела это векторная физическая величина, которая равна произведению скорости тела на его массу. Также импульс тела имеет и второе название это количество движения. Направление импульса тела совпадает с направлением вектора скорости. Импульс тела в системе си не имеет собственной единицы измерения. Поэтому он измеряется в единицах входящих в его состав это килограммометр в секунду кгм/с. Импульс тела, по сути, является новой трактовкой второго закона Ньютона. В котором попросту разложили ускорение.

Кинетическая энергия тела представляет собой скалярную физическую величину равную произведению массы тела на квадрат его скорости деленную пополам. Кинетическая энергия это энергия движения тела. Как видно из формулы она зависит от массы тела и что немаловажно от квадрата его скорости. Кинетическая энергия покоящегося тела равна нулю. Если в формулу подставить ноль в числитель, то и энергия получится, равна нулю. Кинетическая энергия является частью полной энергии тела или системы тел. И она зависит от выбора системы отсчета. Так как в зависимости от того какую мы выберем систему отсчета будет зависеть скорость движения тела.

Механическая работа это энергетическая характеристика движения физических тел, имеющая скалярный вид. Она равна модулю силы действующей на тело, умноженной на модуль перемещения вызванного этой силой и на косинус угла между ними. Данная формула имеет общий вид. В случае если угол между прикладываемой силой и перемещением равен нулю, то косинус равен 1. Соответственно работа будет равна только произведению силы на перемещение. Проще говоря, если тело движется в направлении приложения силы, то механическая работа равна произведению силы на перемещение.

Потенциальная энергия это энергия взаимодействия тел, либо частей тела, между собой. В потенциальном поле консервативных сил. Она зависит от расстояния, на котором находятся тела, и не зависит от их скорости. Таким образом, потенциальная энергия это скалярная величина, имеющая числовое значение, но не имеющая вектора направления. Также она способна совершать работу под действием сил поля. Примером потенциальной энергии можно считать, такую энергию которой обладает тело массой m подвешенное на некотором расстоянии от земли. В данном случае взаимодействуют два тела. Это земля и подвешенный груз.

Закон сохранения энергии, для любой замкнутой системы полная механическая энергия остается постоянной при любых взаимодействиях тел внутри системы. То есть энергия не возникает из ниоткуда и в никуда не исчезает. Она лишь переходит из одной формы в другую. Это справедливо для замкнутых систем, в которых энергия не поступает из вне, и не уходит из системы наружу. Приближённым примером замкнутой системы может служить падение груза относительно большой массы, и малых размеров на землю с небольшой высоты. Допустим, что груз зафиксирован на некоторой высоте. При этом он обладает потенциальной энергией. Эта энергия зависит от его массы и высоты, на которой находится тело.

Относительное движение это движение точки в приделах некоторой системы координат, которая в свою очередь движется относительно другой системы координат являющейся неподвижной. При этом для точки система координат, в которой она движется, является неподвижной. Для описания движения тел можно использовать любую систему отсчета. Как правило, ее выбирают исходя из соображений простоты. То есть выбирается такая система отсчета, в которой данное движение описывается максимально просто. С точки зрения физики все системы отсчета обладают равными правами. Но вот одни и те же характеристики движения в разных системах отсчета будут отличаться.

Источник

Законы сложения сил в механике

При воздействии на одно тело нескольких сил одновременно тело начинает двигаться с ускорением, являющимся векторной суммой ускорений, которые бы возникли под воздействием каждой силы по отдельности. К действующим на тело силам, приложенным к одной точке, применяется правило сложения векторов.

Векторная сумма всех сил, одновременно воздействующих на тело, это сила равнодействующая, которая определяется по правилу векторного сложения сил:

R → = F 1 → + F 2 → + F 3 → + . . . + F n → = ∑ i = 1 n F i → .

Равнодействующая сила действует на тело также, как и сумма всех действующих на него сил.

Правило параллелограмма и правило многоугольника

Для сложения 2 -х сил используют правило параллелограмма (рисунок 1 ).

Рисунок 1 . Сложение 2 -х сил по правилу параллелограмма

Выведем формулу модуля равнодействующей силы с помощью теоремы косинусов:

R → = F 1 → 2 + F 2 → 2 + 2 F 1 → 2 F 2 → 2 cos α

При необходимости сложения более 2 -х сил используют правило многоугольника: от конца
1 -й силы необходимо провести вектор, равный и параллельный 2 -й силе; от конца 2 -й силы необходимо провести вектор, равный и параллельный 3 -й силе и т.д.

Рисунок 2 . Сложение сил правилом многоугольника

Конечный вектор, проведенный от точки приложения сил в конец последней силы, по величине и направлению равняется равнодействующей силе. Рисунок 2 наглядно иллюстрирует пример нахождения равнодействующей сил из 4 -х сил: F 1 → , F 2 → , F 3 → , F 4 → . Причем суммируемые векторы совсем необязательно должны быть в одной плоскости.

Результат действия силы на материальную точку будет зависеть только от ее модуля и направления. У твердого тела есть определенные размеры. Потому силы с одинаковыми модулями и направлениями вызывают разные движения твердого тела в зависимости от точки приложения.

Линией действия силы называют прямую, проходящую через вектор силы.

Рисунок 3 . Сложение сил, приложенных к различным точкам тела

Если силы приложены к различным точкам тела и действуют не параллельно по отношению друг к другу, тогда равнодействующая приложена к точке пересечения линий действия сил (рисунок 3 ). Точка будет находиться в равновесии, если векторная сумма всех сил, действующих на нее, равняется 0 : ∑ i = 1 n F i → = 0 → . В данном случае равняется 0 и сумма проекций данных сил на любую координатную ось.

Разложение вектора силы по направлениям

Разложение сил на две составляющие – это замена одной силы 2 -мя, приложенными в той же точке и производящими на тело такое же действие, как и эта одна сила. Разложение сил осуществляется, как и сложение, правилом параллелограмма.

Задача разложения одной силы (модуль и направление которой заданы) на 2 , приложенные в одной точке и действующие под углом друг к другу, имеет однозначное решение в следующих случаях, когда известны:

• направления 2 -х составляющих сил;
• модуль и направление одной из составляющих сил;
• модули 2 -х составляющих сил.

Пример 1

Необходимо разложить силу F на 2 составляющие, находящиеся в одной плоскости с F и направленные вдоль прямых a и b (рисунок 4 ). Тогда достаточно от конца вектора F провести 2 прямые, параллельные прямым a и b . Отрезок F A и отрезок F B изображают искомые силы.

Рисунок 4 . Разложение вектора силы по направлениям

Второй вариант данной задачи – найти одну из проекций вектора силы по заданным векторам силы и 2 -й проекции (рисунок 5 а ).

Рисунок 5 . Нахождение проекции вектора силы по заданным векторам

Во втором варианте задачи необходимо построить параллелограмм по диагонали и одной из сторон, как в планиметрии. На рисунке 5 б изображен такой параллелограмм и обозначена искомая составляющая F 2 → силы F → .

Итак, 2 -й способ решения: прибавим к силе силу, равную — F 1 → (рисунок 5 в ). В итоге получаем искомую силу F → .

Три силы F 1 → = 1 Н ; F 2 → = 2 Н ; F 3 → = 3 Н приложены к одной точке, находятся в одной плоскости (рисунок 6 а ) и составляют углы с горизонталью α = 0 ° ; β = 60 ° ; γ = 30 ° соответственно. Необходимо найти равнодействующую силу.

Решение

Рисунок 6 . Нахождение равнодействующей силы по заданным векторам

Нарисуем взаимно перпендикулярные оси О Х и O Y таким образом, чтобы ось О Х совпадала с горизонталью, вдоль которой направлена сила F 1 → . Сделаем проекцию данных сил на координатные оси (рисунок 6 б ). Проекции F 2 y и F 2 x отрицательны. Сумма проекций сил на координатную ось О Х равняется проекции на данную ось равнодействующей: F 1 + F 2 cos β — F 3 cos γ = F x = 4 — 3 3 2 ≈ — 0 , 6 Н .

Точно также для проекций на ось O Y : — F 2 sin β + F 3 sin γ = F y = 3 — 2 3 2 ≈ — 0 , 2 Н .

Модуль равнодействующей определим с помощью теоремы Пифагора:

F = F x 2 + F y 2 = 0 , 36 + 0 , 04 ≈ 0 , 64 Н .

Направление равнодействующей найдем при помощи угла между равнодействующей и осью (рисунок 6 в ):

t g φ = F y F x = 3 — 2 3 4 — 3 3 ≈ 0 , 4 .

Сила F = 1 к Н приложена в точке В кронштейна и направлена вертикально вниз (рисунок 7 а ). Необходимо найти составляющие данной силы по направлениям стержней кронштейна. Все необходимые данные отображены на рисунке.

Решение

Рисунок 7 . Нахождение составляющих силы F по направлениям стержней кронштейна

Дано:

F = 1 к Н = 1000 Н

Пускай стержни прикручены к стене в точках А и С . На рисунке 7 б изображено разложение силы F → на составляющие вдоль направлений А В и В С . Отсюда понятно, что

F 1 → = F t g β ≈ 577 Н ;

F 2 → = F cos β ≈ 1155 Н .

Ответ: F 1 → = 557 Н ; F 2 → = 1155 Н .

Источник

Сложение двух сил в теоретической механике — задачи с решением

Сложение двух сил:

Сложение двух сходящихся сил, т. е. сил, линии действия которых пересекаются в одной точке, производится по тем же двум правилам — правилу параллелограмма и правилу треугольника и теми же методами —графическим, графо-аналитическим и аналитическим (методом проекций).

* Как известно, 1 кГ — сила, с которой 1 кг (килограмм массы) притягивается к земле на широте 45° и на уровне моря.

При сложении сил необходимо учитывать следующее обстоятельство.

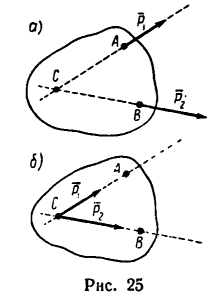
В теоретической механике —в механике твердого тела сила — скользящий вектор, т. е. при решении задач силу можно переносить вдоль линии ее действия в любую точку. Поэтому, если на тело действуют как, например, две силы

Задача:

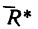
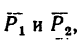
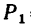
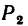
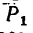
Определить равнодействующую двух сил модули которых соответственно равны = 40 я и = 80 н; сила направлена горизонтально вправо, а Р2 образует с Р, угол а = 120’ (рис. 26, а).

Задачу можно решить графическим или графо-аналитическим методом, используя в обоих случаях либо правило параллелограмма, либо правило треугольника (см. задачи 1-1 и 11-3).

Графическим методом рекомендуем решить задачу самостоятельно, а здесь приведем графо-аналитические решения по обоим правилам.

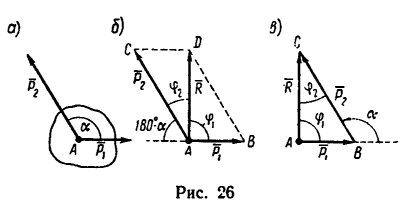
Решение 1-по правилу параллелограмма:

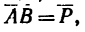
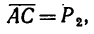
1. Используя условие задачи и приблизительно соблюдая масштаб, изображаем параллелограмм ABCD (рис. 26,6). Порядок построения такой: из точки А проводим отрезок затем из той же точки А под углом 120° к отрезку АВ проводим отрезок из точек В и С проводим прямые BD || АС и CD || АВ и, наконец, проводим диагональ

2. Используя формулу (1), можем найти модуль равнодействующей:

————————————————
* Необходимо помнить, что если в задаче требуется найти какой-либо вектор (в данной задаче R), то это значит, нужно найти модуль вектора и его направление

Имея в виду, что cos 120°= — sin 30°= —0,5, получаем

3. Применяя к A ABD (или к Л ACD) (см. рис. 26,6) теорему синусов, получаем откуда

и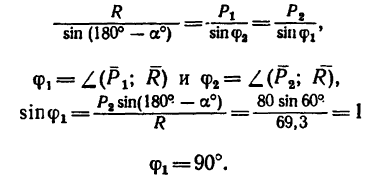
Таким образом, вектор равнодействующей 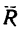перпендикулярен к силе

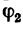
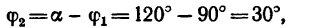
Угол можно найти либо как разность

либо из теоремы синусов: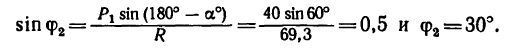

Один и тот же результат, полученный различными путями, подтверждает правильность решения задачи.

Ответ. Равнодействующая данных сил равна 69,3 к, и линия ее действия образует с направлением силы 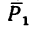прямой угол.

Решение 2-по правилу треугольника.

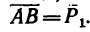
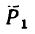
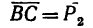
1. Используя условие задачи, строим треугольник сил АВС (рис._26,в). Порядок построения такой: из точки А проведем отрезок Затем из уточки В под углом а =120° к направлению проводим отрезок и, наконец, «замкнем» треугольник отрезком АС, который изобразит искомую равнодействующую R.

В получившемся треугольнике

2. Применяем к треугольнику АВС известную из тригонометрии теорему косинусов:

откуда модуль равнодействующей

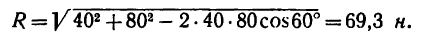
3. Углы 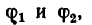определяющие направление равнодействующей относительно заданных сил, находим, как и в первом решении, по теореме синусов.

Необходимо заметить, что в задаче складываются одинаковые по модулю силы, но угол, образуемый их направлениями, уменьшается, и это приводит к увеличению модуля равнодействующей и к уменьшению угла

Рекомендую подробно изучить предмет:

Теоретическая механика

Ещё лекции с примерами решения и объяснением:

• Разложение силы на две составляющие
• Определение равнодействующей сходящихся сил
• Равновесие сходящихся сил
• Равновесие трех непараллельных сил
• Момент количества движения
• Мощность и работа силы
• Потенциальная энергия
• Обобщенные координаты системы

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник