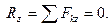Законы сложения сил в механике
При воздействии на одно тело нескольких сил одновременно тело начинает двигаться с ускорением, являющимся векторной суммой ускорений, которые бы возникли под воздействием каждой силы по отдельности. К действующим на тело силам, приложенным к одной точке, применяется правило сложения векторов.
Векторная сумма всех сил, одновременно воздействующих на тело, это сила равнодействующая, которая определяется по правилу векторного сложения сил:
R → = F 1 → + F 2 → + F 3 → + . . . + F n → = ∑ i = 1 n F i → .
Равнодействующая сила действует на тело также, как и сумма всех действующих на него сил.
Правило параллелограмма и правило многоугольника
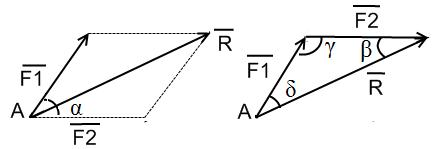
Для сложения 2 -х сил используют правило параллелограмма (рисунок 1 ).
Рисунок 1 . Сложение 2 -х сил по правилу параллелограмма
Выведем формулу модуля равнодействующей силы с помощью теоремы косинусов:
R → = F 1 → 2 + F 2 → 2 + 2 F 1 → 2 F 2 → 2 cos α
При необходимости сложения более 2 -х сил используют правило многоугольника: от конца
1 -й силы необходимо провести вектор, равный и параллельный 2 -й силе; от конца 2 -й силы необходимо провести вектор, равный и параллельный 3 -й силе и т.д.
Рисунок 2 . Сложение сил правилом многоугольника
Конечный вектор, проведенный от точки приложения сил в конец последней силы, по величине и направлению равняется равнодействующей силе. Рисунок 2 наглядно иллюстрирует пример нахождения равнодействующей сил из 4 -х сил: F 1 → , F 2 → , F 3 → , F 4 → . Причем суммируемые векторы совсем необязательно должны быть в одной плоскости.
Результат действия силы на материальную точку будет зависеть только от ее модуля и направления. У твердого тела есть определенные размеры. Потому силы с одинаковыми модулями и направлениями вызывают разные движения твердого тела в зависимости от точки приложения.
Линией действия силы называют прямую, проходящую через вектор силы.
Рисунок 3 . Сложение сил, приложенных к различным точкам тела
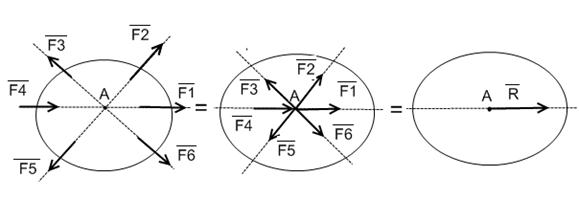
Если силы приложены к различным точкам тела и действуют не параллельно по отношению друг к другу, тогда равнодействующая приложена к точке пересечения линий действия сил (рисунок 3 ). Точка будет находиться в равновесии, если векторная сумма всех сил, действующих на нее, равняется 0 : ∑ i = 1 n F i → = 0 → . В данном случае равняется 0 и сумма проекций данных сил на любую координатную ось.
Разложение вектора силы по направлениям
Разложение сил на две составляющие – это замена одной силы 2 -мя, приложенными в той же точке и производящими на тело такое же действие, как и эта одна сила. Разложение сил осуществляется, как и сложение, правилом параллелограмма.
Задача разложения одной силы (модуль и направление которой заданы) на 2 , приложенные в одной точке и действующие под углом друг к другу, имеет однозначное решение в следующих случаях, когда известны:
- направления 2 -х составляющих сил;
- модуль и направление одной из составляющих сил;
- модули 2 -х составляющих сил.
Пример 1
Необходимо разложить силу F на 2 составляющие, находящиеся в одной плоскости с F и направленные вдоль прямых a и b (рисунок 4 ). Тогда достаточно от конца вектора F провести 2 прямые, параллельные прямым a и b . Отрезок F A и отрезок F B изображают искомые силы.
Рисунок 4 . Разложение вектора силы по направлениям
Второй вариант данной задачи – найти одну из проекций вектора силы по заданным векторам силы и 2 -й проекции (рисунок 5 а ).
Рисунок 5 . Нахождение проекции вектора силы по заданным векторам
Во втором варианте задачи необходимо построить параллелограмм по диагонали и одной из сторон, как в планиметрии. На рисунке 5 б изображен такой параллелограмм и обозначена искомая составляющая F 2 → силы F → .
Итак, 2 -й способ решения: прибавим к силе силу, равную — F 1 → (рисунок 5 в ). В итоге получаем искомую силу F → .
Три силы F 1 → = 1 Н ; F 2 → = 2 Н ; F 3 → = 3 Н приложены к одной точке, находятся в одной плоскости (рисунок 6 а ) и составляют углы с горизонталью α = 0 ° ; β = 60 ° ; γ = 30 ° соответственно. Необходимо найти равнодействующую силу.
Решение
Рисунок 6 . Нахождение равнодействующей силы по заданным векторам
Нарисуем взаимно перпендикулярные оси О Х и O Y таким образом, чтобы ось О Х совпадала с горизонталью, вдоль которой направлена сила F 1 → . Сделаем проекцию данных сил на координатные оси (рисунок 6 б ). Проекции F 2 y и F 2 x отрицательны. Сумма проекций сил на координатную ось О Х равняется проекции на данную ось равнодействующей: F 1 + F 2 cos β — F 3 cos γ = F x = 4 — 3 3 2 ≈ — 0 , 6 Н .
Точно также для проекций на ось O Y : — F 2 sin β + F 3 sin γ = F y = 3 — 2 3 2 ≈ — 0 , 2 Н .
Модуль равнодействующей определим с помощью теоремы Пифагора:
F = F x 2 + F y 2 = 0 , 36 + 0 , 04 ≈ 0 , 64 Н .
Направление равнодействующей найдем при помощи угла между равнодействующей и осью (рисунок 6 в ):
t g φ = F y F x = 3 — 2 3 4 — 3 3 ≈ 0 , 4 .
Сила F = 1 к Н приложена в точке В кронштейна и направлена вертикально вниз (рисунок 7 а ). Необходимо найти составляющие данной силы по направлениям стержней кронштейна. Все необходимые данные отображены на рисунке.
Решение
Рисунок 7 . Нахождение составляющих силы F по направлениям стержней кронштейна
Дано:
F = 1 к Н = 1000 Н
Пускай стержни прикручены к стене в точках А и С . На рисунке 7 б изображено разложение силы F → на составляющие вдоль направлений А В и В С . Отсюда понятно, что
F 1 → = F t g β ≈ 577 Н ;
F 2 → = F cos β ≈ 1155 Н .
Ответ: F 1 → = 557 Н ; F 2 → = 1155 Н .
Источник
Система сходящихся сил



Лекция 2
Системой сходящихся сил (ССС) называется такая система сил, линии действия которых пересекаются в одной точке.
ССС эквивалентна равнодействующей силе, которая равна векторной сумме слагаемых сил. Точка приложения равнодействующей силы совпадает с точкой пересечения линий действия сил.
Решение многих задач механики связано с операциями сложения сил.
Определение. Вектор, равный геометрической сумме системы сил, называется главным вектором системы сил.
Не путать с понятием равнодействующей!
Главный вектор определяется всегда для любой системы сил. Но существуют системы сил, которые нельзя заменить равнодействующей – пара сил, скрещивающиеся силы.
Операции сложения сил и разложение сил на составляющие
1. Сложение двух сил: 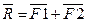
Выполняется по правилу параллелограмма или путем построения силового треугольника.
Модуль силы 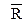
R = 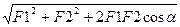
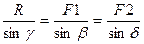
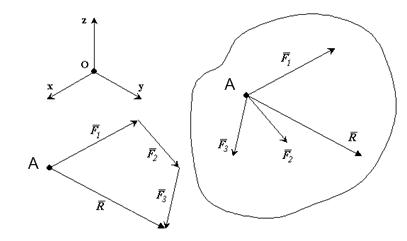
2.Сложение трех сил, не лежащих в одной плоскости: 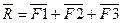
Операция сводится к нахождению диагонали параллелепипеда, построенного на этих силах. В простейшем случае параллелепипед прямоугольный (рис.1-9)
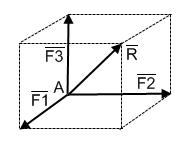 | Модуль вектора находим по формуле: 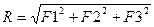 . . |
3.Сложение системы сходящихся сил: 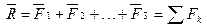
Операция сложения выполняется либо последовательным применением к системе сил правила параллелограмма, либо путем построения силового многоугольника (рис.1-9).
4.Разложение силы на составляющие.
Операция, обратная сложению сил. Может быть выполнена неоднозначно. Необходимо задать направления составляющих сил. Наиболее часто встречаются два случая:
1) Разложение силы на две составляющие: 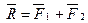
Операция сводится к нахождению сторон параллелограмма, у которого известна диагональ R и углы, образованные с диагональю линиями действия составляющих сил. Ниже показаны три варианта разложения силы на составляющие: 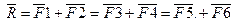
2) Разложение силы на три составляющие, не лежащие в одной плоскости:
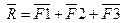
Операция сводится к нахождению сторон параллелепипеда, у которого известной является диагональ.
Аналитический способ нахождения равнодействующей ССС
Аналитические методы решения задач механики основаны на методах проекций.
Аналитический способ задания силы.
В декартовых координатах приложенный в заданной точке А вектор 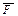
| 1) — задать координаты точки А (x,y,z), — задать модуль вектора F, — задать углы α, β, γ, образованные вектором с осями координат. | 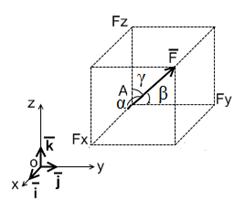 |
2) — задать координаты точки А (x,y,z),
— определить проекции вектора 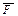
— определить модуль вектора и направляющие косинусы:
F = 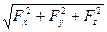
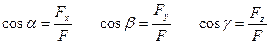
Аналитический способ нахождения равнодействующей
Используется теорема геометрии: Проекция вектора суммы на какую-либо ось равна алгебраической сумме проекций слагаемых сил на ту же ось.
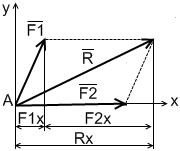 | Равнодействующая ССС находится по правилу параллелограмма: 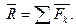 (*) Находим силу (*) Находим силу 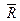 в декартовых координатах вторым способом: в декартовых координатах вторым способом: 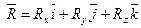 Находим проекции вектора, спроецировав векторное равенство на оси координат: Находим проекции вектора, спроецировав векторное равенство на оси координат: 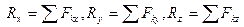 . . |
Модуль равнодействующей и направляющие косинусы:
R =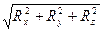
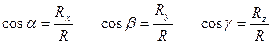
Главный вектор и равнодействующая ССС
Главный вектор и равнодействующая ССС находятся по правилу параллелограмма: 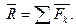
Необходимые и достаточные условия равновесия ССС
Формулируются в геометрической и аналитической форме.
1. Геометрическая форма. Для того, чтобы ССС находилась в равновесии необходимо и достаточно, чтобы главный вектор (равнодействующая) равнялся нулю
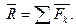
R =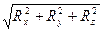
1) 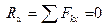
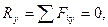
Для того, чтобы ССС находилась в равновесии необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на каждую их трех координатных осей равнялись нулю.
Каждое из условий соответственно означает, что тело под действием ССС не совершает линейные перемещения вдоль координатных осей x,y,z.
Источник