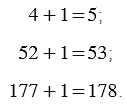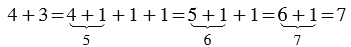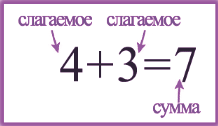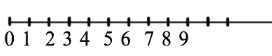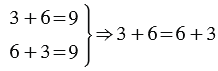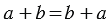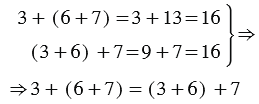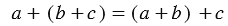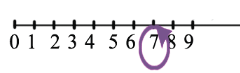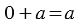Способы сложения натуральных чисел

Сложение натуральных чисел

К нескольким натуральным числам прибавим 1:

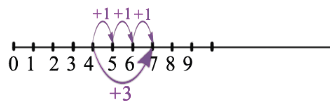
Мы видим, что когда мы прибавляем к натуральному числу 1, получаем следующее за ним натуральное число, т.е. следующее число больше предыдущего на единицу. Теперь к 4 прибавим 3: 4+3: для этого к 4 прибавим 3 раза единицу. Учитывая, что при прибавлении к числу единицы получаем следующее число, получим:

Но мы записываем коротко: 4+3=7.

Числа, которые складываются, называются слагаемыми, число, которое получается в результате сложения, называется суммой.

Сложение чисел на координатном луче

Изобразим координатный луч. Отметим на нем начало координат, единичный отрезок и несколько чисел, следующих друг за другом:

Рассмотрим наш пример: 4+3. Для того чтобы к 4 прибавить 3 на координатном луче, необходимо от точки 4 вправо отложить 3 единичных отрезка:

И мы попадем в точку 7, следовательно 4+3=7.

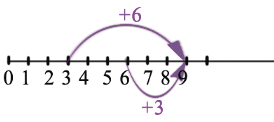
Теперь попробуем отложить на луче, от точки 3 6 единичных отрезков, и от точки 6 3 единичных отрезка, другими словами к 3 прибавим 6 и к 6 прибавим 3 :

Мы видим, что и в первом и во втором случае мы попадаем в одну и ту же точку: 9, следовательно сумма чисел 3 и 6 и 6 и 3 одинакова и равна 9. Это можно записать с помощью равенства:

В этом случае мы меняем местами слагаемые и получаем первое свойство сложения — переместительное свойство :

• От перестановки слагаемых сумма не меняется

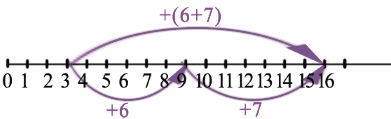
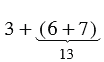
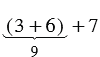
Рассмотрим с помощью координатного луча следующие суммы: и , для этого от точки 3 сначала отложим (6+7) единичных отрезков, а затем от точки 3, отложим сначала 6 единичных отрезков, а затем от получившийся точки отложим еще 7 единичных отрезков:

Заметим, что и в первом и во втором случае мы попадаем в одну точку: 16. Это можно записать равенством:

Мы получили второе свойство сложения — сочетательное свойство:

• Чтобы прибавить к числу сумму двух чисел, можно сначала прибавить первое слагаемое, а потом к полученной сумме прибавить второе слагаемое

К натуральному числу можно прибавлять не только натуральное число, но еще и нуль, изобразим на луче прибавление нуля к 7:

Так как нам необходимо отложить от точки 0 единичных отрезков, то мы попадаем снова в ту же точку,т.е. значение числа от прибавления к нему нуля не изменилось: 7+0=7 . Применив переместительное свойство получим: 7+0=0+7=7, отсюда получаем третье свойство сложения — свойство нуля:

• Если прибавить к нулю какое-нибудь число, то получится прибавленное число

Свойства сложения

1. Переместительное свойство

От перестановки слагаемых сумма не меняется

1. Сочетательное свойство

Чтобы прибавить к числу сумму двух чисел, можно сначала прибавить первое слагаемое, а потом к полученной сумме прибавить второе слагаемое

1. Свойство нуля

Если прибавить к нулю какое-нибудь число, то получится прибавленное число

Сравнение сумм натуральных чисел

Сравним (15+81) и (15+77), для этого рассмотрим слагаемые этих двух сумм: Мы видим, что первые слагаемые у них одинаковые, поэтому переходим к сравнению вторых слагаемых: 81 >77, поэтому (15+81)>(15+77).

Теперь сравним (21+15) и (34+54), для этого опять рассмотрим слагаемые, в данном случае одинаковых у нас нет, но мы видим, что слагаемые первой суммы меньше слагаемых второй суммы, а значит мы можем записать: (21+15) При увеличении слагаемых сумма увеличивается, а при уменьшении уменьшается.

Письменный прием сложения («сложение в столбик»)

Часто при решении задач, нам необходимо складывать многозначные числа, поэтому считать в «уме» или чертить координатный луч не целесообразно, для решения таких задач был придуман письменный прием сложения или «сложение в столбик», который помогает сложение многозначных чисел свести к сложению однозначных чисел, которое мы можем производить легко. Рассмотрим пример:

1	1	1
+	4	5	8	7	1
	4	3	8	2
5	0	2	5	3

Сложение начинаем справа, с разряда единиц: 1+2=3, записываем 3 под единицами, и переходим в разряд десятков: 7+8=15 >10, значит единицы десятков(5) записываем под десятками, а десяток десятков — это единица сотен, записываем ее над разрядом сотен, чтобы не забыть и переходим в следующий разряд: 8+3+ 1 =12 >10, поступаем аналогично, единицы(2) записываем под рассматриваемым разрядом, а десятки записываем над следующим разрядом, далее складываем единицы тысяч: 5+4+ 1 =10=10, здесь 0 единиц, поэтому под рассматриваемым разрядом ставим нуль, а десяток переносим в разряд десятков тысяч: 4+ 1 =5. Получаем, что 45871+4382=50253.

Вывод: Если при сложении чисел одного разряда число получается больше или равное 10, то 1 десяток записываем над следующим разрядом, а единицы под рассматриваемым разрядом.

Поделись с друзьями в социальных сетях:

Источник

Способы быстрого сложения и вычитания натуральных чисел

Главная > Документ

Информация о документе
Дата добавления:
Размер:
Доступные форматы для скачивания:

Способы быстрого сложения и вычитания натуральных чисел.

Если одно из слагаемых увеличить на несколько единиц, то из полученной суммы надо вычесть столько же единиц.

364+592=364+(592+8) – 8=364+600 – 8=956.

Если одно из слагаемых увеличить на несколько единиц, а второе уменьшить на столько же единиц, то разность не изменится.

Если вычитаемое увеличить на несколько единиц и уменьшаемое увеличить на столько же единиц, то разность не изменится.

1351 – 994=(1351+6) – (994+6)=1357 – 1000=357.

Если от суммы двух чисел отнять разность тех же чисел, то в результате получится удвоенное меньшее число, т. е. (a+b) – (a – b)=2b.

Если к сумме двух чисел прибавить их разность, то в результате получится удвоенное большее число, т. е. (a+b) + (a – b)=2a.

Сложение столбцами . Сумма цифр каждого разряда складывается отдельно. Цифра десятков в сумме предыдущего разряда складывается с цифрой единиц последующей суммы.

Способы быстрого умножения и деления натуральных чисел.

Применение распределительного закона умножения относительно сложения и вычитания к множителям, один из которых представлен в виде суммы или разности.

7·196=7·(200 – 4)=1400 – 28=1372.

Умножение методом Ферроля . Для получения единиц произведения перемножают единицы множителей, для получения десятков умножают десятки одного на единицы другого множителя и наоборот и результаты складывают, для получения сотен перемножают десятки. Этот способ умножения следует из тождества (10a+b)(10c+d)=100ac+10(ad+bc)+bd.

37·48=1776 а) 8·7=56, пишем 6, помним 5;

б) 8·3+4·7+5=57, пишем 7, помним 5;

в) 4·3+5=17, пишем 17.

Методом Ферроля легко перемножать устно двузначные числа от 10 до 20.

12·14=168. Умножаем так:

а)2·4=8; б) 1·2+1·4=6; в) 1·1=1.

Можно умножить и трехзначное число на двузначное.

а)3·5=15, пишем 5, помним 1;

б) (3·2+2·5)+1=17, пишем 7, помним 1;

в) (3·1+2·2)+1=8, пишем 8;

Умножение чисел, у которых число десятков одинаково, а сумма единиц равна 10 . Число десятков любого множителя умножить на число, которое больше на 1, затем перемножить отдельно единицы этих чисел и, наконец, к первому результату справа приписать второй. Этот способ основан на тождестве (10a+b)·(10a+c)=100a(a+1)+bc, где b+c=10.

13·17=221, а)1·(1+1)=2, пишем 2;

б) 3·7=21, приписываем справа 21.

204·206=42024, а)20·(20+1)=420, пишем 420;

б)6·4=24, приписываем справа 24.

Умножение чисел на 11. Записать последнюю цифру числа (цифру из разряда единиц), затем последовательно, справа налево записывать суммы соседних двух цифр множимого и, наконец, первую цифру множимого.

54·11=594; а) пишем 4;

Если одна из сумм соседних цифр окажется больше 9, то на соответствующем месте записывают цифру единиц полученной суммы, а к следующей сумме прибавляют 1. Прибавляют единицу и к последней цифре множителя, если предыдущая сумма превышала 9.

58·11=638, а) пишем 8;

б) 5+8=13, пишем 3, помним 1;

3765·11=41415, а) пишем 5;

б) 5+6=11, пишем 1, помним 1;

в) (7+6)+1=14, пишем 4, помним 1;

г) (3+7)+1=11, пишем 1, помним 1;

Умножение на числа вида aa . Умножить данное число сначала на а, потом на 11.

Умножение двузначного числа на 111. Справа налево нужно последовательно записать: последнюю цифру первого множителя (т. е. цифру из разряда единиц), сумму цифр первого множителя, снова сумму его цифр и, наконец, его первую цифру. Если сумма цифр двузначного числа больше 9, то записываем цифру единиц каждой суммы, а к следующему результату прибавляем 1.

68·111=7548, а) пишем последнюю цифру 8;

б) 6+8=14, пишем 4, помним 1;

в) (6+8)+1=15, пишем 5, помним 1;

Умножение на 5, 25, 125. Разделить число соответственно на 2, 4, 8 и результат умножить на 10, 100, 1000.

Если множитель не делится на 2, 4 или на 8, то деление производится с остатком. Затем частное умножают соответственно на 10, 100 или 1000, а остаток – на 5, 25 или 125.

53·5=26·10+1·5=265 (53:2=26 и 1 в остатке);

43·25=10·100+3·25=1075 (43:4=10 и 3 в остатке);

66·125=8·1000+2·125=8250 (66:8=8 и 2 в остатке).

Деление на 5, 25, 125 . Умножить число соответственно на 2, 4, 8 и разделить на 10, 100, 1000.

Иногда удобно менять порядок действий, выполняя сначала деление на 10, 100, 1000, а потом умножение.

Умножение на 9, 99 и 999 . К первому множителю приписать столько нулей, сколько девяток во втором множителе, и из результата вычесть первый множитель.

Возведение в квадрат двузначных чисел, имеющих 5 десятков. К 25 прибавить цифру в разряде единиц и к результату приписать справа квадрат числа единиц так, чтобы получилось четырехзначное число. Этот способ основан на тождестве (50+а) 2 =100·(25+а)+а 2 .

51 2 =2601, а) 25+1=26, пишем 26;

б) 1 2 =1, приписываем 01.

58 2 =3364, а) 25+8=33, пишем 33;

б) 8 2 =64, приписываем 64.

Возведение в квадрат двузначных чисел, оканчивающихся цифрой 5. Число десятков умножаем на следующее за ним натуральное число, справа приписываем число 25.

Источник

Свойства сложения и вычитания

О чем эта статья:

Свойства сложения

Сложение — это арифметическое действие, в котором единицы двух чисел объединяются в одно новое число

Для записи сложения используют знак «+» (плюс), который ставят между слагаемыми.

Слагаемые — это числа, единицы которых складываются.

Сумма — это число, которое получается в результате сложения.

Рассмотрим пример 2 + 5 = 7, в котором:

• 2 — это первое слагаемое,
• 5 — второе слагаемое,
• 7 — это сумма.

При этом саму запись (2 + 5) можно тоже назвать суммой.

Сложение двух чисел можно проверить вычитанием. Для этого вычитаем из суммы одно из слагаемых. Если разность окажется равной другому слагаемому — сложение выполнено верно.

Впервые мы сталкиваемся со свойствами сложения во 2 классе. С каждым годом задания усложняются, и появляются новые правила и законы. Рассмотрим свойства сложения для 4 класса.

1. Переместительное свойство сложения
   От перестановки мест слагаемых сумма не меняется.
   a + b = b + a
2. Сочетательное свойство сложения
   Чтобы к сумме двух чисел прибавить третье нужно к первому числу прибавить сумму второго и третьего числа.
   (a + b) + c = a + (b + c)
3. Свойство нуля при сложении
   Если к числу прибавить нуль, получится само число.
   a + 0 = 0 + a = a

Свойства вычитания

Вычитание— это арифметическое действие, в котором отнимают меньшее число от большего.

Для записи вычитания используется знак «-» (минус), который ставится между уменьшаемым и вычитаемым.

Уменьшаемое — это число, из которого вычитают.

Вычитаемое — это число, которое вычитают.

Разность — это число, которое получается в результате вычитания.

Рассмотрим пример 9 — 4 = 5, в котором:

9 — это уменьшаемое,

4 — вычитаемое,

5 — разность.

При этом саму запись (9 — 4) тоже можно назвать разностью.

1. Свойство нуля при вычитании
   Если из числа вычесть нуль, получится само число.
   a — 0 = a
   Если из числа вычесть само число, то получится нуль.
   a — a = 0
2. Свойство вычитания суммы из числа
   Чтобы вычесть сумму из числа, можно вычесть из этого числа одно слагаемое, из полученной разности — второе слагаемое.
   a — (b + c) = a — b — c
3. Свойство вычитания числа из суммы
   Чтобы вычесть число из суммы, можно вычесть его из одного слагаемого, а к результату прибавить оставшееся слагаемое.
   (a + b) — c = (a — c) + b (если a > c или а = с)
   (a + b) — c = (b — c) + a (если b > c или b = с)

Примеры использования свойств сложения и вычитания

Мы узнали основные свойства сложения и вычитания — осталось попрактиковаться. Чтобы ничего не забыть, используйте эту шпаргалку:

Пример 1

Вычислить сумму слагаемых с использованием разных свойств:

а) 4 + 3 + 8 = (4 + 3) + 8 = 7 + 8 = 15

б) 9 + 11 + 2 = (9 + 2) + 11 = 11 + 11 = 22

в) 30 + 0 + 13 = 30 + 13 = 43

Пример 2

Применить разные свойства при вычислении разности:

а) 25 — 0 — 2 = 25 — 2 = 23

б) 18 — (1 + 4) = 18 — 1 — 4 = 17 — 4 = 13

Пример 3

Найти значение выражения удобным способом:

а) 11 + 10 + 3 + 9 = (11 + 10) + (3 + 9) = 21 + 11 = 32

б) 16 — (4 + 3) + 7 = 16 — 4 — 3 + 7 = (16 — 4) — 3 + 7 = 12 — 3 + 7 = 9 + 7 = 16

Источник