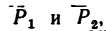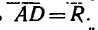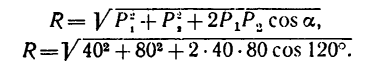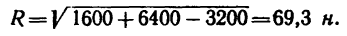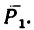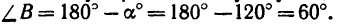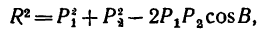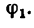Способы сложения двух сил это

Сложение сил

Способы сложения сил:

Если две или более сил направлены в одну сторону, их просто складывают. Вы толкаете автомобиль и его толкают еще несколько человек в ту же сторону, силы складываются, автомобиль катится.

Или если все вместе поднимают тяжелый шкаф или телевизор. В одну сторону действует подъемная сила, а в противоположную сторону сила тяжести. Тогда происходит вычитание силы тяжести из ваших сил. И только когда ваша совокупная сила подъема станет больше силы тяжести, телевизор будет поднят.

Если силы будут одинаковыми, но разнонаправленными, то тело будет оставаться в покое: кто-то толкает тело с одной стороны, кто-то с другой, если сила равна, тело останется на месте.

Редактировать этот урок и/или добавить задание Добавить свой урок и/или задание

Добавить интересную новость

Добавить анкету репетитора и получать бесплатно заявки на обучение от учеников

user->isGuest) < echo (Html::a('Войдите', ['/user/security/login'], ['class' =>»]) . ‘ или ‘ . Html::a(‘зарегистрируйтесь’, [‘/user/registration/register’], [‘class’ => »]) . ‘ , чтобы получать деньги $$$ за каждый набранный балл!’); > else < if(!empty(\Yii::$app->user->identity->profile->first_name) || !empty(\Yii::$app->user->identity->profile->surname))< $name = \Yii::$app->user->identity->profile->first_name . ‘ ‘ . \Yii::$app->user->identity->profile->surname; > else < $name = ''; >echo ‘Получайте деньги за каждый набранный балл!’; > ?>—>

Добавление комментариев доступно только зарегистрированным пользователям

Lorem iorLorem ipsum dolor sit amet, sed do eiusmod tempbore et dolore maLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborgna aliquoLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempbore et dLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborlore m mollit anim id est laborum.

28.01.17 / 22:14, Иван Иванович Ответить +5

Lorem ipsum dolor sit amet, consectetu sed do eiusmod qui officia deserunt mollit anim id est laborum.

28.01.17 / 22:14, Иван ИвановичОтветить -2

Lorem ipsum dolor sit amet, consectetur adipisicing sed do eiusmod tempboLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod temLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborpborrum.

28.01.17 / 22:14, Иван Иванович Ответить +5

Источник

Сложение двух сил в теоретической механике — задачи с решением

Сложение двух сил:

Сложение двух сходящихся сил, т. е. сил, линии действия которых пересекаются в одной точке, производится по тем же двум правилам — правилу параллелограмма и правилу треугольника и теми же методами —графическим, графо-аналитическим и аналитическим (методом проекций).

* Как известно, 1 кГ — сила, с которой 1 кг (килограмм массы) притягивается к земле на широте 45° и на уровне моря.

При сложении сил необходимо учитывать следующее обстоятельство.

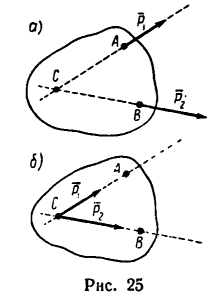
В теоретической механике —в механике твердого тела сила — скользящий вектор, т. е. при решении задач силу можно переносить вдоль линии ее действия в любую точку. Поэтому, если на тело действуют как, например, две силы

Задача:

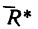
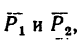
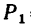
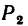
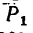
Определить равнодействующую двух сил модули которых соответственно равны = 40 я и = 80 н; сила направлена горизонтально вправо, а Р2 образует с Р, угол а = 120’ (рис. 26, а).

Задачу можно решить графическим или графо-аналитическим методом, используя в обоих случаях либо правило параллелограмма, либо правило треугольника (см. задачи 1-1 и 11-3).

Графическим методом рекомендуем решить задачу самостоятельно, а здесь приведем графо-аналитические решения по обоим правилам.

Решение 1-по правилу параллелограмма:

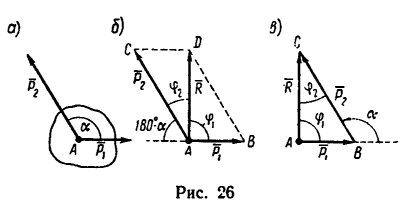
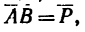
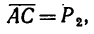
1. Используя условие задачи и приблизительно соблюдая масштаб, изображаем параллелограмм ABCD (рис. 26,6). Порядок построения такой: из точки А проводим отрезок затем из той же точки А под углом 120° к отрезку АВ проводим отрезок из точек В и С проводим прямые BD || АС и CD || АВ и, наконец, проводим диагональ

2. Используя формулу (1), можем найти модуль равнодействующей:

————————————————
* Необходимо помнить, что если в задаче требуется найти какой-либо вектор (в данной задаче R), то это значит, нужно найти модуль вектора и его направление

Имея в виду, что cos 120°= — sin 30°= —0,5, получаем

3. Применяя к A ABD (или к Л ACD) (см. рис. 26,6) теорему синусов, получаем откуда

и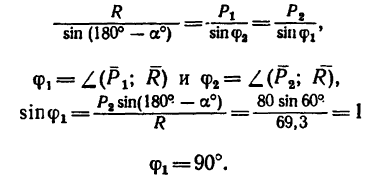
Таким образом, вектор равнодействующей 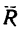перпендикулярен к силе

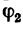
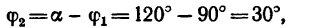
Угол можно найти либо как разность

либо из теоремы синусов: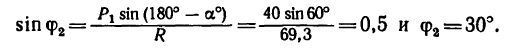

Один и тот же результат, полученный различными путями, подтверждает правильность решения задачи.

Ответ. Равнодействующая данных сил равна 69,3 к, и линия ее действия образует с направлением силы 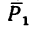прямой угол.

Решение 2-по правилу треугольника.

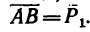
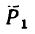
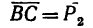
1. Используя условие задачи, строим треугольник сил АВС (рис._26,в). Порядок построения такой: из точки А проведем отрезок Затем из уточки В под углом а =120° к направлению проводим отрезок и, наконец, «замкнем» треугольник отрезком АС, который изобразит искомую равнодействующую R.

В получившемся треугольнике

2. Применяем к треугольнику АВС известную из тригонометрии теорему косинусов:

откуда модуль равнодействующей

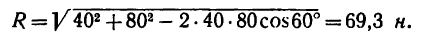
3. Углы 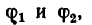определяющие направление равнодействующей относительно заданных сил, находим, как и в первом решении, по теореме синусов.

Необходимо заметить, что в задаче складываются одинаковые по модулю силы, но угол, образуемый их направлениями, уменьшается, и это приводит к увеличению модуля равнодействующей и к уменьшению угла

Рекомендую подробно изучить предмет:

Теоретическая механика

Ещё лекции с примерами решения и объяснением:

• Разложение силы на две составляющие
• Определение равнодействующей сходящихся сил
• Равновесие сходящихся сил
• Равновесие трех непараллельных сил
• Момент количества движения
• Мощность и работа силы
• Потенциальная энергия
• Обобщенные координаты системы

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Техническая механика. Конспекты лекций (стр. 3 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

Модуль равнодействующей двух сил можно определить из треугольника ACD:

На основании четвертой аксиомы одну силу F∑ можно заменять двумя составляющими силами F1 и F2. Такую замену часто производят при решении задач статики.

Пятая аксиома устанавливает, что в природе не может быть одностороннего действия силы. При взаимодействии тел всякому действию соответствует равное и противоположно направленное противодействие. Так, если на тело В действует сила F1 со стороны материального тела А, то на тело А действует со стороны тела В такая же по численному значению сила F2. Обе силы действуют по одной прямой и направлены в противоположные стороны. Действие и противодействие всегда приложены к различным телам, и именно поэтому они не могут уравновешиваться(рис.6).

Рис.6 Иллюстрации к пятой аксиоме статики

4 Связи и их реакции

Рассматриваемые в механике тела могут быть свободными и несвободными. Свободным называют тело, которое не испытывает никаких препятствий для перемещения в пространстве в любом направлении. Если же тело связано с другими телами, которые ограничивают его движение в одном или нескольких направлениях, то оно является несвободным. Тела, которые ограничивают движение рассматриваемого тела, называют связями.

При взаимодействии между телом и его связями возникают силы, противодействующие возможным движениям тела. Эти силы действуют на тело со стороны связей и называются реакциями связей.

Реакция связи всегда противоположна тому направлению, по которому связь препятствует движению тела. Существование реакций обосновывается аксиомой о действии и противодействии. Для определения реакций связей используют принцип освобождения от связей. Не изменяя равновесия тела, каждую связь можно отбросить, заменив ее реакцией. Определение реакций связей является одной из наиболее важных задач статики. Ниже приведены наиболее распространенные виды связей, встречающиеся в задачах:

1. Связь в виде гладкой (т. е. без трения) плоскости или поверхности. В этом случае реакция связи всегда направлена по нормали к опорной поверхности (рис.7а).

2. Связь в виде контакта цилиндрической или шаровой поверхности с плоскостью. В этом случае реакция связи направлена также по нормали к опорной поверхности (рис.7б).

3. Cвязь в виде шероховатой плоскости. Здесь возникают две составляющие реакции: нормальная Rn, перпендикулярная плоскости, и касательная Rt, лежащая в плоскости. Касательная реакция Rt называется силой трения и всегда направлена в сторону, противоположную действительному или возможному движению тела.
Полная реакция R, равная геометрической сумме нормальной и касательной составляющих R=Rn+Rt, отклоняется от нормали к опорной поверхности на некоторый угол р. При взаимодействии тела с реальными связями возникают силы трения. Однако во многих случаях силы трения незначительны и вследствие этого ими часто пренебрегают (рис.7в).

4. Гибкая связь, осуществляемая веревкой, тросом, цепью и т. п. (рис.7г). Реакции гибких связей направлены вдоль связей, причем гибкая связь может работать только на растяжение.

5. Связь в виде жесткого прямого стержня с шарнирным закреплением концов. Здесь реакции всегда направлены вдоль осей стержней. Стержни при этом могут быть как растянутыми, так и сжатыми (рис.7д).

6. Связь, осуществляемая ребром двугранного угла или точечной опорой. Реакция такой связи направлена перпендикулярно поверхности опирающегося тела (рис.7е).

Рис.7 Виды связей.

Тема 1.2 Плоская система сходящихся сил

Лекция № 3 «Плоская система сходящихся сил»

1. Плоская система сходящихся сил

Рис. 8 Силовой многоугольник

Рассмотрим равновесие системы сходящихся сил. Сходящимися называются силы, линии действия которых пере­секаются в одной точке (рис. 8а). Существуют два способа сложения пересекающихся сил: геометрический (рис. 8б) и аналитический (рис. 8в).

Геометрический способ сложения сходящихся сил.

От произвольной точки О откладываем вектор, равный силе 1; от конца 1 откладываем вектор, равный силе 2, и т. д. (см. рис.8, а, б). Затем, соединяя начало вектора 1 с концом последнего 4, получаем равнодействующую всех сил. Построенная фигу­ра называется силовым многоугольником.

Аналитический метод сложения сходящихся сил. Проектируя векторное равенство 1+2+3= на оси коорди­нат, получим два алгебраических равенства:

Flx + F2x + F3x = Rx;

F1 cos 1 — F2 cos 2 — F3 cos 3 = — R cos .

Отсюда определим значение равнодействующей всех сходящихся сил:

и направление вектора :

Условием равновесия системы сходящихся сил является равен­ство нулю модуля равнодействующей , т. е. силовой многоуголь­ник должен быть замкнутым (при геометрическом способе сложе­ния) или, аналитически, проекции равнодействующей силы на оси координат должны быть равны нулю (Rx = Ry = 0). Отсюда для плоской системы сходящихся сил получим два уравнения равнове­сия этих сил:

Следовательно, для равновесия системы сходящихся сил необхо­димо и достаточно, чтобы сумма проекций всех сил на каждую из осей координат была равна нулю.

Метод проекций

Осью называют прямую линию, которой приписано определенное направление. Проекция вектора на ось является скалярной величиной, которая определяется отрезком оси, отсекаемым перпендикулярами, опущенными на нее из начала и конца вектора.

Рис.9 Виды проекций

Проекция вектора считается положительной (+), если направление от начала проекции к ее концу совпадает с положительным направлением оси. Проекция вектора считается отрицательной (—), если направление от начала проекции к ее концу противоположно положительному направлению оси.

Тема 1.3 Пара сил и момент силы относительно точки

Лекция № 4 «Пара сил. Момент силы»

Парой сил называют две силы и равные по величине, противоположно направленные и параллельные между собой (рис. 10).

Сила, действующая на тело, может не только смещать его, но и поворачивать вокруг какой-нибудь точки. Пусть сила , приложенная в точке А, стремится повернуть тело вокруг точки О (рис. 10). Поскольку силу можно переносить по линии ее действия, то вращательный эффект этой силы не будет зависеть от того, в какой точке эта сила приложена, и будет зависеть от расстояния h от точки О до линии действия силы.

Моментом силы F относительно некоторого центра О называ­ется величина, равная произведению силы на кратчайшее рас­стояние от точки О до линии действия силы и взятая с соответст­вующим знаком. Знак «плюс» соответствует моменту силы, кото­рая стремится повернуть тело вокруг точки О против хода часо­вой стрелки, а знак «минус» — если сила стремится повернуть тело по направлению движения часовой стрелки. Если линия действия силы проходит через точку, то момент силы относительно этой точки равен нулю. Перпендикуляр, опущенный из точки О на линию действия си­лы , называется ее плечом относительно центра О.

Источник