Способы синтеза математических моделей

Методы получения математических моделей

Математическая модель

Математическая модель — это математическое представление реальности, представляющее собой частный случай понятия модели, как системы, исследование которой позволяет получать информацию о некоторой другой системе.

Процесс построения и изучения математических моделей называется математическим моделированием.

Все естественные и общественные науки, использующие математический аппарат, по сути занимаются математическим моделированием: заменяют объект его математической моделью и затем изучают последнюю. Связь математической модели с реальностью осуществляется с помощью цепочки гипотез, идеализаций и упрощений.

Математическую модель объекта удобно представить в виде блок-схемы, т.е. параметрической схемы, в которой прямоугольник соответствует объекту или системе, стрелки X, Х(t) означают вход­ные параметры (факторы) или воздействия на систему, а стрелки У, У(t) — выходные параметры. На схеме внутри прямоугольника вписывают оператор или динамическую характеристику.

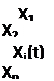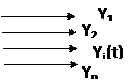Рис. 1 Блок-схема математической модели

Зная математическую модель процесса или объекта, можно спрогнозировать свойства выходящего продукта, оценить степень влияния входных факторов с целью разработки схемы контроля и стабилизации наиболее сильно влияющих факторов, а также осу­ществить оптимизацию процесса.

Математическая модель считается адекватной объекту, если с достаточной точностью отражает ее поведение, т.е. изменения вы­ходных параметров при варьировании (изменении) входных пара­метров (факторов) в заранее заданном диапазоне.

В основу классификации математических моделей положены следующие признаки:

1. Число и характеристика аргументов :

а) если входные параметры процесса или оператор не зависят от аргументов, то математическая модель называется статической. Этот вид модели обычно описывается алгебраическим уравнением:

б) если входные параметры процесса или оператор зависят от аргументов, то такая модель называется динамической. Если пара­метр процесса или оператор зависит только от одного аргумента, например, от времени Х==Х(t), модель называется динамической мо­делью с сосредоточенными параметрами, т.е.

Эти модели описываются обыкновенными дифференциальны­ми уравнениями;

в) если число независимых аргументов более одного (например, время и пространственные координаты), то такая модель называется математической моделью с распределенными параметрами, т.е.

Эти модели описываются дифференциальными уравнениями в частных производных.

2. Природа исследуемого процесса или объекта. По этому признаку модели делятся на вероятностные и детерминированные.

В вероятностной модели учитывается случайная природа входных параметров или оператора. Вероятностные модели могут быть нескольких видов:

а) если выходной параметр процесса представляет случайную величину, а факторы (входные параметры) являются не случайными, то математическая модель называется регрессионной (регрессия — движение назад). Случайные значения выходного параметра могут быть обусловлены, например, воздействием части неучтенных факто­ров. Эта модель позволяет предполагать, что причина изменения вы­ходного параметра содержит в себе две части: одна неслучайная, яв­ляется функцией факторов; другая случайная, не связана с факторами.

При построении регрессионных моделей используются раз­личные виды алгебраических уравнений;

б) если выходной параметр процесса и факторы представляют случайные величины с определенным законом распределения, то взаимосвязь между ними или математическая модель процесса назы­вается корреляционной (корреляция — соотношение). В этом случае к вопросам выяснения зависимости между случайными величинами параметров процесса еще добавляются вопросы исследования степе­ни связи между ними, и при построении этих моделей используется корреляционный анализ случайных величин;

в) в детерминированной модели не учитывается случайная природа входных параметров процесса или оператора, а выходные параметры процесса однозначно определяются факторами и опера­тором процесса. В этом случае не требуются математико-статистические методы анализа процесса.

3. Свойство линейности модели. Математическая модель на­зывается линейной, если линеен оператор системы. Оператор А < >называется линейным, если выполняется равенство

где DХ — символ произвольного приращения входных параметров.

Это свойство линейного оператора называется также свой­ством суперпозиции, или наложения. Если это равенство не выпол­няется, то оператор и соответственно модель называется нелинейной.

Методы получения математических моделей

Методы получения математических моделей подразделяются на теоретические и экспериментальные.

Теоретический метод заключается в аналитическом исследова­нии физической сущности процесса с использованием общих законов физики, или процессов с использованием уравнений материального и энергетического баланса.

Применение чисто теоретического метода представляет боль­шую трудность вследствие сложности явлений, происходящих в про­цессах, или недостаточной степени изученности их.

Экспериментальный метод математического описания заклю­чается в обработке экспериментальных данных, полученных непо­средственно на действующих объектах производства, или на полу­промышленной лабораторной машине, или физической модели про­цесса — стенде.

Наиболее эффективным методом получения математической модели является сочетание теоретического и экспериментальных ме­тодов. При этом на долю теоретического метода приходится анализ в основном структурных свойств объекта и продуктов и получение общего вида уравнений, а на долю экспериментального — количе­ственный анализ и проверка теоретических выводов.

Источник

Методы получения математических моделей.

1.Аналитический метод основан на изучение физических и химических процессов, происходящих в объектах с учетом конструкции объекта и характеристик материала. При этом используются известные законы сохранения энергии вещества, кинетики и т.д.

Преимущества данного метода: модели получаются универсальные, их можно использовать на аналогичных объектах большего или меньшего размера.

Недостаток: объекты управления настолько сложны, что описать известными уравнениями все происходящие процессы при реальных граничных условиях не удается, а если и удается, решение получается очень сложным.

В таких случаях говорят, модель не замкнута, т.е. количество уравнений меньше количества неизвестных.

2.Экспериментальный (опытный) основан на опытных исследованиях объекта управления и дает возможность получить математическое описание таких объектов, аналитическое описание которых не возможно.

Экспериментальные методы делятся на:

а) пассивные. Предполагают изучение свойств объекта в процессе нормальной эксплуатации объекта, т.е. объект не останавливается, выпускает продукцию, а анализируются естественные, случайные колебания входных и выходных величин. Используются методы обработки случайных процессов.

Недостаток: точность модели будет не высока.

б) активные. Подразумевают специальные воздействия на объект с дальнейшим изучением реакции выходных величин (отклика).

Недостаток: при этих экспериментах процесс выходит за пределы оптимального режима.

Метод отличается высокой точностью.

3.Комбинированный (экспериментально-аналитический). Суть метода в том, что в начале используя известные законы сохранения, получают систему уравнений в общем виде, т.е. коэффициенты на данном этапе предполагаются неизвестные. А на втором этапе путем эксперимента получают коэффициенты.

Адекватность модели — соответствие математической модели тем процессам, которые изучаются; в соответствии определяются погрешности, когда теоретические данные не соответствуют экспериментальным.

Лекция № 9 Системы автоматического управления технологическими процессами.

Информация по текущему состоянию снимается датчиками.

Сигналы пропорциональные измерению передаются на щит управления.

Технологический персонал, управляющий вычислительный комплекс (УВК).

УВК состоит из УСО (устройства связи с объектом).

МПС – электронный мозг УВК (микропроцессорная система). УВК может обмениваться информацией с помощью модема.

АСУП – автоматизированная система управления предприятием.

Эксплуатационный персонал АСУП может вносить коррективы в работу УВК.

Станции управления регуляторов служат для переключения с ручного режима управления на автоматическое регулирование и наоборот. Кроме того, на станции управления находятся манипуляторы для ручного управления исполнительными механизмами (ИМ). ИМ является приводом регулирующего органа.

В зависимости от использования вычислительной машины возможны следующие режимы:

1. Машина, т.е. УВК используется в качестве многоканального цифрового прибора (информационно-справочный режим), управление при этом ручное.

2. Супервизорный режим. Здесь наряду с автоматическим регулированием машина автоматически изменяет заданные значения (задания) регуляторов, тем самым осуществляется супервизорное автоматическое управление.

3. Режим непосредственного цифрового управления. Здесь регуляторы уже не работают. Управление происходит непосредственно от машины, минуя регуляторы. Сигнал идет от станции управления к исполнительному механизму.

1-ый и 3-ий режимы являются одноуровневыми. В первом случае работает только нижний уровень, а в третьем — только верхний уровень. Второй режим – двухуровневый. Нижний уровень – регуляторы, верхний уровень – УВК.

Источник

Методы построения математических моделей

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Моделирование — процедура получения информации об управляемом объекте из информации о воздействиях и информации о состояниях, а также исследования информации об управляемом объекте.

Моделирование как способ исследования существующих в природе объектов представляет собой цепь из чередующихся вопросов и ответов, экспериментов — вопросов к природе и моделей — ответов природы экспериментатору.

В процессе моделирования происходит абстрагирование (мысленное отвлечение) от ряда несущественных свойств объекта в целях выделения наиболее существенных, а также образования новых абстрактных понятий. Ограничения и допущения, применяемые при построении и использовании каждой модели, являются ее составной частью.

Моделирование включает в себя четыре основных этапа:

1) разработку гипотезы о виде и размере модели (формулирование вопроса к природе);

2) планирование эксперимента (шифрование вопроса);

3) контроль состояния управляемого в эксперименте объекта (фиксирование экспериментатором ответа природы);

4) параметрическую идентификацию модели управляемого объекта, включающую в себя обработку опытных данных (расшифровку ответа).

Информация об управляемой системе

Информация об управляемом объекте представляется в виде математической модели управляемого объекта. Математическая модель — наиболее удобный заменитель объекта в системе управления, имеющий с этим объектом общие наиболее существенные свойства. Математическая модель представляет собой систему математических соотношений между параметрами и факторами, а также ограничения на них.

По способу получения математические модели делятся на теоретические и эмпирические.

Теоретические математические модели — модели, получаемые путем логического анализа и формализации общих закономерностей управляемого объекта.

Эмпирические математические модели — модели, получаемые путем аппроксимации (приближения) функций, характеризующих управляемый объект, наиболее употребительными функциями.

Теоретические модели могут быть заданы конечными алгебраическими или трансцендентными уравнениями, обыкновенными дифференциальными уравнениями и дифференциальными уравнениями в частных производных.

Виды эмпирических моделей более разнообразны. Наиболее часто применяются простые алгебраические уравнения.

По степени изменчивости управляемого объекта математические модели делятся на статические и динамические.

Статические математические модели — модели, не учитывающие фактор времени.

Динамические математические модели — модели, учитывающие фактор времени.

Статические математические модели применяются для описания стационарных процессов в управляемых объектах, то есть процессов, параметры которых не обнаруживают существенных изменений с течением времени.

Динамические математические модели применяются для описания нестационарных процессов в управляемых объектах, то есть процессов, параметры которых закономерно изменяются с течением времени.

По степени стабильности управляемого объекта математические модели делятся на детерминированные и стохастические.

Детерминированные математические модели — модели, в которых параметры управляемого объекта являются определенными величинами, то есть в разных случаях приобретают одни и те же значения.

Стохастические математические модели — модели, в которых параметры управляемого объекта являются случайными величинами, то есть в разных случаях приобретают различные значения.

Стохастические математические модели применяют для описания случайных процессов, параметры которых являются случайными функциями.

По форме математические модели делятся на полиномиальные и мультипликативные.

Полиномиальные математические модели — модели, представленные в виде суммы одночленов различных степеней. Например, линейные, квадратные, кубические и другие.

Мультипликативные математические модели — модели, представленные в виде произведения степенных, экспоненциальных и экспоненциально-степенных функций.

По степени исследованности управляемого объекта математические модели делятся на три группы:

1. Теоретические модели достаточно исследованных объектов известной структуры с известными параметрами. Эти математические модели готовы к непосредственному использованию в системе управления.

2. Теоретические и эмпирические модели недостаточно исследованных объектов известной структуры с неизвестными параметрами. Математические модели этой группы получают путем параметрической идентификации.

3. Эмпирические модели неисследованных объектов неизвестной структуры с неизвестными параметрами. Такие математические модели получают путем идентификации с использованием принципа «черного ящика».

На практике чаще всего применяют идентифицируемые математические модели (2-го или 3-го типа).

С известными параметрами

С неизвестными параметрами

Рис. 4. Виды математических моделей

Математические модели должны удовлетворять следующим требованиям:

· Адекватность. Наиболее существенные свойства модели и управляемого объекта должны быть тождественны.

· Изоморфность. Форма описания всех параметров управляемого объекта должна быть одинаковой.

· Полнота. Модель должна содержать все управляющие факторы и все обуславливаемые параметры управляемого объекта, необходимые для решения задачи управления.

· Надежность. Модель должна оставаться справедливой на протяжении всего отрезка времени, на котором решается задача управления.

Методы построения математических моделей

Теоретические модели получают в результате логического анализа и формализации общих закономерностей исследуемого процесса. В основу метода построения теоретических моделей входят логическое обобщение имеющихся фактов и логический вывод результатов из небольшого числа основных принципов, законов и гипотез.

Использование аппарата математики и логики дает возможность понять внутреннюю структуру объекта исследования и повысить уровень достоверности знания о природе объекта.

Взаимосвязь и взаимозависимость различных величин, характеризующих разные по своей природе процессы, выражаются с помощью математических функций, полученных в результате математических преобразований.

Процесс подбора эмпирической формулы для устанавливаемой в эксперименте зависимости R = f(z) состоит из двух процедур: подбора вида формулы и установления численных значений ее параметров, для которых приближение к этой формуле оказывается наилучшим.

Если нет каких-либо соображений для подбора вида формулы, то выбирают функциональную зависимость из числа наиболее простых, сравнивая их графики с графиком идентифицируемой функции.

При рассмотрении графиков следует иметь в виду, что при пользовании эмпирическими формулами используется лишь часть кривой, соответствующая некоторому интервалу изменения аргумента.

К числу наиболее употребительных функций, применяемых при моделировании, относятся линейные, квадратные, кубические, степенные, экспоненциальные и экспоненциально-степенные.

Могут быть рекомендованы:

а) линейные полиномиальные модели

;

б) квадратные полиномиальные модели

;

в) кубические полиномиальные модели

;

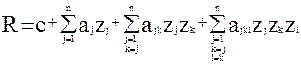
г) экспоненциальные мультипликативные модели

.

Экспоненциальные мультипликативные модели логарифмированием приводят к линейным полиномиальным моделям

;

д) степенные мультипликативные модели

.

е) экспоненциально-степенные мультипликативные модели

.

Экспоненциально-степенные мультипликативные модели логарифмированием приводят к линейным полиномиальным моделям

.

Для описания случайных величин используют различные функции распределения. Среди этих распределений: экспоненциальное, степенное, Гнеденко и другие.

Функция распределения F(x) — вероятность появления значения случайной величины, не превышающего некоторого заданного х.

Рис. 5. Графики наиболее употребительных функций

Дата добавления: 2018-10-27 ; просмотров: 2842 ; Мы поможем в написании вашей работы!

Источник