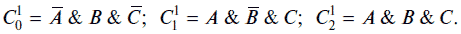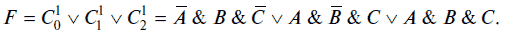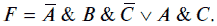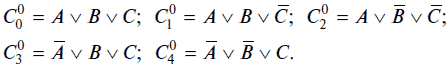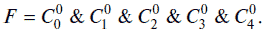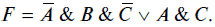История науки и техники Com New
Логические элементы и синтез логических схем
Сложные цифровые логические устройства, входящие в состав компьютера, состоят из ряда элементарных логических элементов, построенных на базе средств электронной техники. При производстве этих электронных логических элементов используют различные технологии и схемотехнические решения, такие как: ДТЛ (диодно-транзисторная логика), ТТЛ (транзисторно-транзисторная логика), ЭСЛ (эмиттерно-связанная логика), технологии, основанные на использовании полевых транзисторов, и т. д. Логические элементы позволяют реализовать любую логическую функцию. Входные и выходные сигналы логических элементов, соответствующие двум логическим состояниям 1 и 0, могут иметь один из двух установленных уровней электрического напряжения, который зависит от схемотехнического решения логического элемента. Например, для логических элементов, основанных на технологии ТТЛ, высокий уровень электрического напряжения (2,4 ? 5 В) соответствует значению логической единицы (истина), а низкий уровень (0 ? 0,4 В) – логическому нулю (ложь).
Три приведенных ниже логических элемента составляют функционально полную систему для проектирования цифровых логических устройств, в том числе и соответствующих логических блоков и устройств компьютера, поскольку реализуют функционально полный набор логических функций, состоящий из логических функций: И (конъюнкции), ИЛИ (дизъюнкции), НЕ (отрицания).
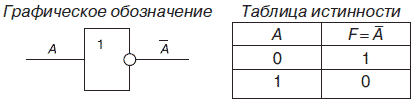
1. Логический элемент НЕ, который называется также инвертором, выполняет логическую операцию отрицания (инверсии).
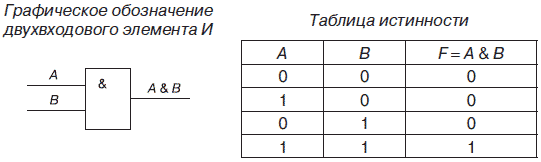
2. Логический элемент И, называемый также конъюнктором, выполняет операцию логического умножения (конъюнкции), теоретически может иметь бесконечное число входов, на практике ограничиваются числом входов от двух до восьми.
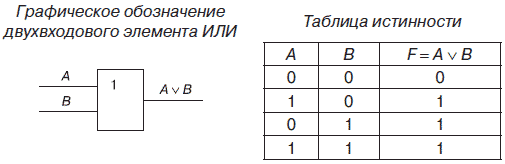
3. Логический элемент ИЛИ, называемый также дизъюнктором, выполняет операцию логического сложения (дизъюнкции), теоретически может иметь бесконечное число входов, на практике ограничиваются числом входов от двух до восьми.
При проектировании цифровых логических устройств часто возникает задача по заданной таблице истинности записать выражение для логической функции и реализовать ее в виде логической схемы, состоящей из функционально полного набора логических элементов. Данную задачу называют также задачей синтеза логических схем или логических устройств.
Синтез логических схем на основе функционально полного набора логических элементов состоит из представления логических функций, описывающих данные логические схемы в нормальных формах. Нормальной формой представления считается форма, полученная посредством суперпозиций вспомогательных логических функций – минтермов и макстернов.
Минтермом называют логическую функцию, которая принимает значение логической единицы только при одном значении логических переменных и значение логического нуля при других значениях логических переменных. Например, минтермами являются логические функции F, F, F и F (см. рис. 4.3).
Макстерном называют логическую функцию, которая принимает значение логического нуля только при одном значении логических переменных и значение логической единицы при других значениях логических переменных. Например, макстернами являются логические функции F, F, F и F (см. рис. 4.3).
Из минтермов и макстернов методом суперпозиции можно составить логические функции, которые называются соответственно логической функцией, представленной посредством совершенных дизъюнктивных нормальных форм (СДНФ), и логической функцией, представленной посредством совершенных конъюнктивных нормальных форм (СКНФ). Полученные таким образом функции СДНФ и СКНФ будут представлять искомую логическую функцию по заданной таблице истинности. После получения функций СДНФ и СКНФ их необходимо преобразовать (минимизировать). Преобразование данных функций с целью их минимизации осуществляется с помощью законов алгебры логики и специальных разработанных методов: метод Квайна, карты Карно, диаграммы Вейча и т. д.
Рассмотрим задачу синтеза на примере модифицированной таблицы истинности, приведенной на рис. 4.6. Для данной таблицы истинности необходимо записать выражение для выходной функции F, провести ее преобразование (минимизацию) на основе законов алгебры логики и, используя основные логические элементы – НЕ, И и ИЛИ, разработать логическую схему реализации выходной функции F.
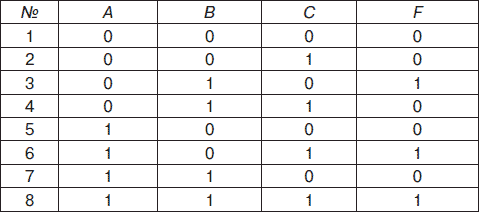
Рис. 4.6. Таблица истинности логических переменных A, В и С
Значения логических переменных А, В и С и соответствующие значения функции F приведены в таблице истинности (см. рис. 4.6), где в столбце № – указан номер комбинации логических переменных A, В и С.
Для решения указанной задачи представим логическую функцию F в виде СДНФ, а затем и в СКНФ. Найдем вспомогательные функции минтермы и макстермы. В заданной таблице истинности выходная функция F принимает логическое значение, равное логической единице, при комбинациях логических переменных A, В и С, указанных под номерами 3, 6, 8, а значение, равное логическому нулю – при комбинациях, указанных под номерами 1, 2, 4, 5,7.
Минтермы запишем в следующем виде:
Минтермы представляют собой логические произведения (конъюнкции) логических переменных А, В, и С при значениях логической функции F, равных логической единице (комбинации 3, 6, 8). Сомножители (логические переменные A, В и С) входят в минтерм в прямом виде (без отрицания), если их значения равны логической единице, и в инверсном (с отрицанием), если их значения равны логическому нулю. Логическая функция F в СДНФ будет равна логической сумме минтермов:
После минимизации логической функции Fc использованием законов алгебры логики получим ее искомое выражение:
Макстермы запишем в следующем виде:
Макстермы представляют собой логические суммы (дизъюнкции) логических переменных А, В, и С при значениях логической функции F, равных логическому нулю (комбинации 1, 2, 4, 5, 7). Слагаемые (логические переменные A, В, и С) входят в макстерм в прямом виде (без отрицания), если их значения равны логическому нулю, и в инверсном (с отрицанием), если их значения равны логической единице. Логическая функция F в СКНФ будет равна логическому произведению макстермов:
Поскольку полученное выражение для F в виде СКНФ является более громоздким по сравнению с представлением F в виде СДНФ, то в качестве окончательного выражения для F примем ее выражение в виде СДНФ, т. е.
Аналогичным образом можно получить выражение для любой логической функции, которая представлена с помощью заданной таблицы истинности с Означениями логических переменных.
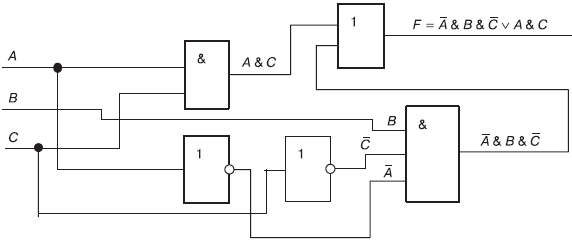
Используем полученное выражение логической функции F для разработки (построения) логической схемы на основе функционально полного набора логических элементов НЕ, И и ИЛИ. При построении логической схемы необходимо учитывать установленные в алгебре логики правила (приоритеты) для выполнения логических операций, которые в данном случае реализуются с помощью логических элементов НЕ, И и ИЛИ. Порядок производимых логических операций будет следующий: операция инверсии (отрицания), операция логического умножения (конъюнкции) и затем операция логического сложения (дизъюнкции). Реализация функции F в виде логической схемы, приведена на рис. 4.7.
Рис. 4.7. Реализация функции F в виде логической схемы
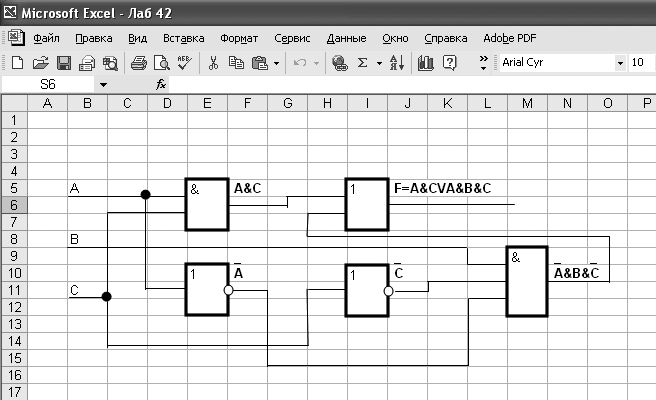
Для графического отображения логических схем существуют различные компьютерные программы, называемые графическими редакторами. Данные программы могут быть включены в другие компьютерные программы, например в программах Microsoft Word и Microsoft Excel такие редакторы реализованы с помощью панелей инструментов «Рисование», или быть самостоятельными программами, например Paint, Microsoft Visio и т. д. Воспользуемся встроенным графическим редактором (панель «Рисование») программы MS Excel для графического отображения логической схемы функции F. Данная логическая схема показана на рис. 4.8.
Рис. 4.8. Графическое отображение логической функции F с помощью программы MS Excel
На основе функционально полного набора логических элементов построены различные электронные устройства, входящие в состав компьютера. К таким устройствам относятся сумматоры (выполняющие операции сложения двоичных чисел), триггеры (устройства, имеющие два устойчивых состояния: логического нуля и логической единицы и используемые в качестве двоичных элементов памяти), регистры памяти (состоящие из набора триггеров), двоичные счетчики, селекторы (переключатели сигналов), шифраторы, дешифраторы и т. д.
Рассмотренные выше таблицы истинности логических элементов показывают установившиеся значения логических переменных. Однако когда логические переменные представлены в виде электрических сигналов, то необходимо некоторое время для того, чтобы значение логической функции достигло уровня установившегося состояния из-за внутренних задержек по времени в электронных логических элементах. В среднем задержка электрического сигнала такого элемента составляет 10 с. В компьютере двоичные сигналы проходят через множество электронных схем, и задержка по времени может стать значительной. В этом случае выделяется отрезок времени (такт) на каждый шаг логической операции. Если операция заканчивается раньше, чем заканчивается тактовое время, то устройство, входящее в состав компьютера, ожидает ее окончания. В результате скорость выполнения операций несколько снижается, но достигается высокая надежность, так как обеспечивается синхронизация между многими параллельно выполняющимися операциями в компьютере. Синхронизация устройств в компьютере обеспечивается с помощью специального генератора – генератора тактовой частоты, который вырабатывает электрические импульсы стабильной частоты.
Предыдущая глава 
Оглавление Следующая глава
Источник
Синтез логических схем
Лабораторная работа выполняется с помощью учебного лабораторного стенда LESO2.
1 Цель работы
Научиться синтезировать логические схемы по заданной таблице истинности.
2 Краткие теоретические сведения
Любая логическая схема без памяти полностью описывается таблицей истинности. Эта таблица является исходной информацией для синтеза схемы на основе логических элементов «И», «ИЛИ», «НЕ». Для разработки требуемого цифрового устройства сначала на основе таблицы истинности записывают его логическое выражение. Затем с целью упрощения цифрового устройства минимизируют его логическое выражение и далее разрабатывают схему, реализующую полученное логическое выражение. Логические выражения можно получить двумя способами:
- на основе совершенной дизъюнктивной нормальной формы (СДНФ);
- на основе совершенной конъюнктивной нормальной формы (СКНФ).
Совершенная дизъюнктивная нормальная форма (СДНФ)
Функция представляется суммой групп. Каждая группа состоит из произведения, в которую входят все переменные.
Например:
f(x1,x2,x3) = x1 ·x2·x3 + x1· x2 ·x3 + x1·x2· x3
Совершенная конъюнктивная нормальная форма (СКНФ)
Функция представляется произведением групп. Каждая группа состоит из суммы, в которую входят все переменные.
Например:
f(x1,x2,x3) = ( x1 +x2+x3)·(x1+ x2 +x3)·(x1+x2+ x3 )
Если схема имеет несколько выходов, то каждый выход описывается своей функцией. Такая система функций называется системой собственных функций. СДНФ составляется на основе таблицы истинности по следующему правилу: для каждого набора переменных, при котором функция равна 1, записывается произведение, в котором с отрицанием берутся переменные, имеющие значение «0».
Пример:
Таблица 2.1 – Заданная таблица истинности
| x1 | x2 | x3 | y |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
y = f(x1,x2,x3) = x1 · x2 ·x3 + x1 ·x2·x3 + x1·x2· x3 + x1·x2·x3
СКНФ составляется на основе таблицы истинности по правилу: для каждого набора переменных, при котором функция равна 0, записывается сумма, в которой с отрицанием берутся переменные, имеющие значение 1.
Таблица 2.2 – Заданная таблица истинности
| x1 | x2 | x3 | y |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
y = f(x1,x2,x3) = (x1+x2+x3)·(x1+ x2 +x3)·( x1 +x2+x3)·( x1 +x2+ x3 )
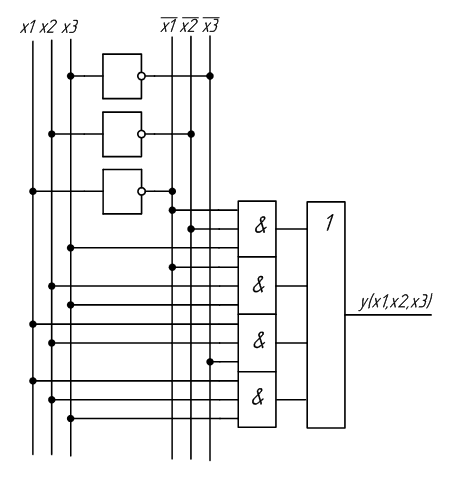
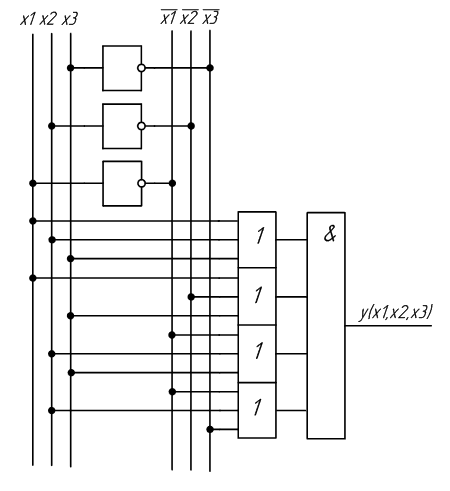
На основе полученных выражений можно составить схему устройства, реализующего заданную функцию. Схема устройства, полученная на основе СДНФ, изображена на рисунке 2.1, а на основе СКНФ на рисунке 2.2.
Рисунок 2.1 – Схема устройства, полученная на основе СДНФ
Рисунок 2.2 – Схема устройства, полученная на основе СКНФ
С целью упрощения цифрового устройства применяют минимизацию функций. Используя законы алгебры логики, можно упростить исходную функцию.
y(x1,x2,x3) = x1 · x2 ·x3 + x1 ·x2·x3 + x1·x2· x3 + x1·x2·x3 =
= x1 ·x3·( x2 +x2) + x1·x2·( x3 +x3) = x1 ·x3 + x1·x2
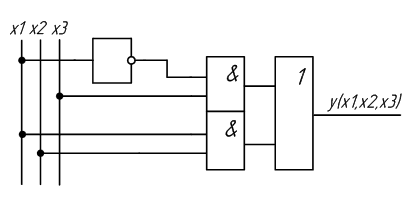
На основе полученного выражения составим новую схему устройства (рисунок 2.3).
Рисунок 2.3 – Схема устройства, полученная после минимизации логической функции
3 Задание к работе
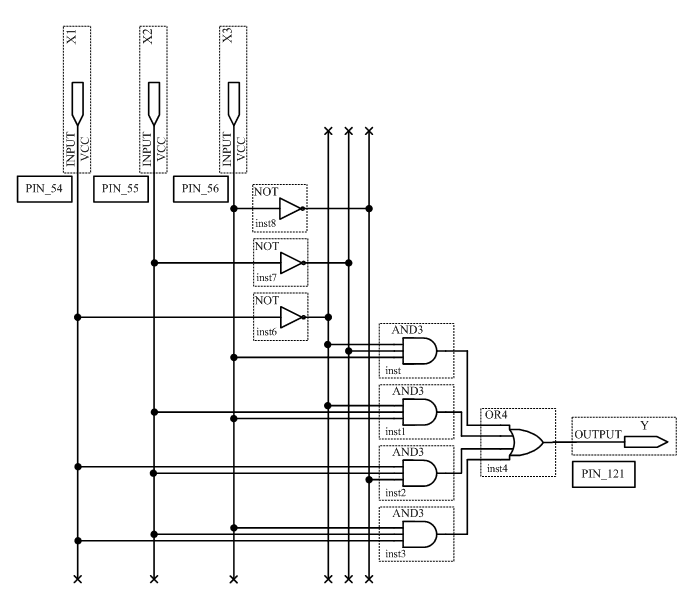
3.1 Исследовать схему, полученную по таблице истинности (таблица 2.1) на основе СДНФ. Для этого сконфигурировать ПЛИС в соответствии со схемой рисунок 2.1. Подключить к входам схемы переключатели S7,S8,S9, а к выходу светодиод LED 8. Схема устройства в среде Quartus II будет выглядеть в соответствии с рисунком 3.1.
Рисунок 3.1 – Схема устройства в среде Quartus II, составленная на основе СДНФ
Устанавливая на входах схемы с помощью переключателей все возможные кодовые комбинации и наблюдая за светодиодом, заполнить таблицу истинности исследуемого устройства.
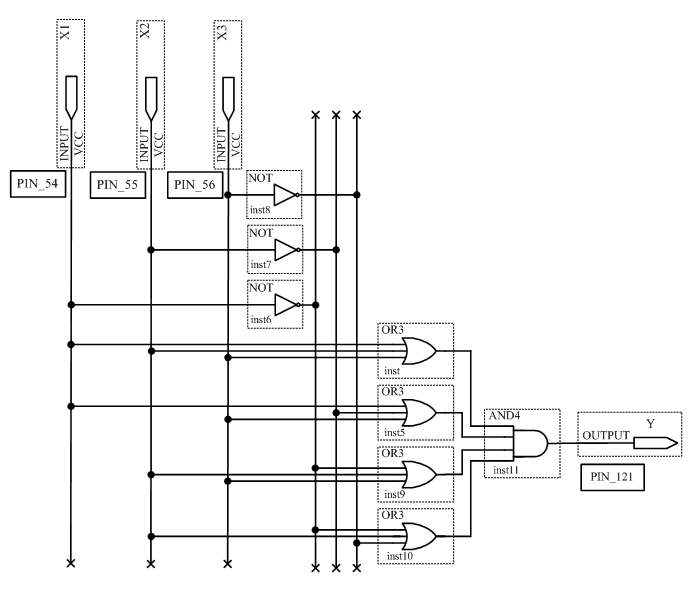
3.2 Исследовать схему, полученную по таблице истинности (таблица 2.2) на основе СКНФ.
Для этого сконфигурировать ПЛИС в соответствии со схемой рисунок 2.2. Подключить к входам схемы переключатели S7,S8,S9, а к выходу светодиод LED 8. Схема устройства в среде Quartus II будет выглядеть в соответствии с рисунком 3.2. Можно не создавать новый проект, а отредактировать проект, созданный в пункте 3.1. Устанавливая на входах схемы с помощью переключателей все возможные кодовые комбинации и наблюдая за светодиодом, заполнить таблицу истинности исследуемого устройства.
Рисунок 3.2 – Схема устройства в среде Quartus II, составленная на основе СКНФ
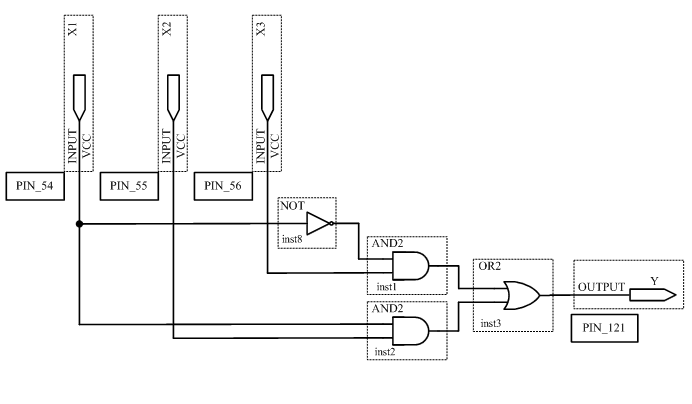
3.3 Исследовать минимизированную схему (рисунок 2.3.)
Для этого сконфигурировать ПЛИС в соответствии со схемой рисунок 2.3. Подключить к входам схемы переключатели S7,S8,S9, а к выходу светодиод LED 8. Схема устройства в среде Quartus II будет выглядеть в соответствии с рисунком 3.3. Устанавливая на входах схемы с помощью переключателей все возможные кодовые комбинации и наблюдая за светодиодом, заполнить таблицу истинности устройства.
Рисунок 3.3 – Схема устройства в среде QUARTUS II, составленная на основе СДНФ с последующей минимизацией.
4 Содержание отчета
- Цель работы.
- Заданная таблица истинности.
- Логическое выражение на основе СДНФ.
- Логическое выражение на основе СКНФ.
- Минимизированное логическое выражение.
- Схемы, синтезированные на основе СДНФ, СКНФ и в результате минимизации.
- Таблицы истинности, полученные в результате исследования схем.
- Выводы.
5 Контрольные вопросы
- Что такое СДНФ?
- Что такое СКНФ?
- Как записать СДНФ, используя таблицу истинности устройства?
- Как записать СКНФ, используя таблицу истинности устройства?
- Как разработать схему логического устройства, используя СДНФ?
- Как разработать схему логического устройства, используя СКНФ?
- Как лучше синтезировать логическое устройство (на основе СДНФ или СКНФ), если значение функции в таблице истинности имеет больше нулей, чем единиц?
- Как разработать логическое устройство, если оно имеет несколько выходов?
- Что такое минимизация логического выражения?
- Запишите основные законы алгебры логики.
- Расскажите, как определить таблицу истинности логического устройства экспериментально, используя лабораторный стенд.
Узнать больше об аппаратном синтезе логическ схем в ПЛИС можно из статьи
Архитектура ПЛИС. Часть 1. Логический элемент
Источник
